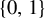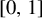1 Introduction
In this paper, a topologically dynamical system (t.d.s. for short) is a pair
![]() $(X, T)$
, where X is a compact metric space endowed with a metric d and
$(X, T)$
, where X is a compact metric space endowed with a metric d and
![]() $T: X \to X$
is a homeomorphism. Denote by
$T: X \to X$
is a homeomorphism. Denote by
![]() $\mathcal {M}(X,T)$
the set of all T-invariant Borel probability measures on X, which is a non-empty convex and compact metric space with respect to the weak
$\mathcal {M}(X,T)$
the set of all T-invariant Borel probability measures on X, which is a non-empty convex and compact metric space with respect to the weak
![]() $^*$
topology. We say a sequence
$^*$
topology. We say a sequence
![]() $\xi $
is realized in
$\xi $
is realized in
![]() $(X,T)$
if there is an
$(X,T)$
if there is an
![]() $f\in C(X)$
and an
$f\in C(X)$
and an
![]() $x\in X$
such that
$x\in X$
such that
![]() $\xi (n) = f(T^nx)$
for any
$\xi (n) = f(T^nx)$
for any
![]() $n\in \mathbb {N}$
. A sequence
$n\in \mathbb {N}$
. A sequence
![]() $\xi $
is said to be deterministic if it is realized in a t.d.s. with zero topological entropy. The Möbius function
$\xi $
is said to be deterministic if it is realized in a t.d.s. with zero topological entropy. The Möbius function
![]() $\mu : \mathbb {N}\rightarrow \{-1,0,1\}$
is defined by
$\mu : \mathbb {N}\rightarrow \{-1,0,1\}$
is defined by
![]() $\mu (1)=1$
and
$\mu (1)=1$
and
 $$ \begin{align} \mu(n)= \begin{cases} (-1)^k & \text{if }n\text{ is a product of }k \text{ distinct primes} \\ 0 & \text{otherwise.} \end{cases} \end{align} $$
$$ \begin{align} \mu(n)= \begin{cases} (-1)^k & \text{if }n\text{ is a product of }k \text{ distinct primes} \\ 0 & \text{otherwise.} \end{cases} \end{align} $$
In this paper,
![]() $\mathbb {N}=\{1,2,\ldots \}$
,
$\mathbb {N}=\{1,2,\ldots \}$
,
![]() $\mathbb {E}$
(respectively
$\mathbb {E}$
(respectively
![]() ${\mathbb {E}}^{\log }$
) stands for a finite average (respectively a finite logarithmical average), that is,
${\mathbb {E}}^{\log }$
) stands for a finite average (respectively a finite logarithmical average), that is,
 $$ \begin{align*}\displaystyle\mathbb{E}_{n\le N}A_n= \frac1{N} \sum_{n=1}^{N}A_n\quad\text{and}\quad \displaystyle\mathbb{E}^{\log}_{n\le N}A_n= \frac1{\sum_{n=1}^N({1}/{n})}\sum_{n=1}^{N}\frac{A_n}{n}.\end{align*} $$
$$ \begin{align*}\displaystyle\mathbb{E}_{n\le N}A_n= \frac1{N} \sum_{n=1}^{N}A_n\quad\text{and}\quad \displaystyle\mathbb{E}^{\log}_{n\le N}A_n= \frac1{\sum_{n=1}^N({1}/{n})}\sum_{n=1}^{N}\frac{A_n}{n}.\end{align*} $$
Here is the well-known conjecture by Sarnak [Reference Sarnak19].
Sarnak Conjecture. The Möbius function
![]() $\mu $
is linearly asymptotically disjoint from any deterministic sequence
$\mu $
is linearly asymptotically disjoint from any deterministic sequence
![]() $\xi $
. That is,
$\xi $
. That is,
The conjecture in the case when X is finite is equivalent to the prime number theorem in arithmetic progressions. The conjecture in the case when T is a rotation on the circle is equivalent to Davenport’s theorem [Reference Davenport2]. The conjecture in many other special cases has been established recently (see [Reference Green and Tao8, Reference Ferenczi, Kułaga-Przymus and Lemańczyk6, Reference Kanigowski, Lemańczyk and Radziwiłł12, Reference Kułaga-Przymus and Lemańczyk13] and references therein).
Tao introduced and investigated the following logarithmic version of the Sarnak conjecture [Reference Tao21, Reference Tao22] (see also [Reference Frantzikinakis and Host7, Reference McNamara18, Reference Tao and Teräväinen23, Reference Tao and Teräväinen24]).
Logarithmic Sarnak Conjecture. For any topological dynamical system
![]() $(X,T)$
with zero entropy, any continuous function
$(X,T)$
with zero entropy, any continuous function
![]() $f:X\to \mathbb {C}$
, and any point x in X,
$f:X\to \mathbb {C}$
, and any point x in X,
Now we let
![]() $(X,T)$
be a t.d.s. with a metric d. For any
$(X,T)$
be a t.d.s. with a metric d. For any
![]() $n\in \mathbb {N}$
, we consider the so-called mean metric induced by d:
$n\in \mathbb {N}$
, we consider the so-called mean metric induced by d:
 $$ \begin{align*}\overline{d}_n(x,y)=\frac{1}{n}\sum_{i=0}^{n-1}d(T^ix,T^iy)\end{align*} $$
$$ \begin{align*}\overline{d}_n(x,y)=\frac{1}{n}\sum_{i=0}^{n-1}d(T^ix,T^iy)\end{align*} $$
for any
![]() $x,y\in X$
. For
$x,y\in X$
. For
![]() $\epsilon>0$
and a subset K of X, we let
$\epsilon>0$
and a subset K of X, we let
 $$ \begin{align*}S_n(d, T,K ,\epsilon)=\min \bigg\{ m\in \mathbb{N}:\text{there exists } x_1,x_2,\ldots,x_m \text{ such that }K\subset\bigcup_{i=1}^m B_{\overline{d}_n}(x_i,\epsilon)\bigg\},\end{align*} $$
$$ \begin{align*}S_n(d, T,K ,\epsilon)=\min \bigg\{ m\in \mathbb{N}:\text{there exists } x_1,x_2,\ldots,x_m \text{ such that }K\subset\bigcup_{i=1}^m B_{\overline{d}_n}(x_i,\epsilon)\bigg\},\end{align*} $$
where
![]() $B_{\overline {d}_n}(x,\epsilon ):=\{y\in X: \overline {d}_n(x,y)<\epsilon \}$
for any
$B_{\overline {d}_n}(x,\epsilon ):=\{y\in X: \overline {d}_n(x,y)<\epsilon \}$
for any
![]() $x\in X$
. We say
$x\in X$
. We say
![]() $(X,T)$
has polynomial mean complexity if there exists a constant
$(X,T)$
has polynomial mean complexity if there exists a constant
![]() $k>0$
such that
$k>0$
such that
![]() $\liminf \nolimits _{n\to +\infty }({S_n(d,T,X,\epsilon )}/ {n^k})=0$
for all
$\liminf \nolimits _{n\to +\infty }({S_n(d,T,X,\epsilon )}/ {n^k})=0$
for all
![]() $\epsilon>0$
. The following is our main result.
$\epsilon>0$
. The following is our main result.
Theorem 1.1. The following statements are equivalent.
-
(1) The logarithmic Sarnak conjecture holds.
-
(2) The logarithmic Sarnak conjecture holds for any t.d.s. with polynomial mean complexity.
-
(3) The logarithmic Sarnak conjecture holds for any
 $\{0,1\}$
-symbolic system with polynomial mean complexity.
$\{0,1\}$
-symbolic system with polynomial mean complexity.
We now briefly describe the main ingredients in the proof of Theorem 1.1. It is clear that statement (1) implies statement (2) which in turn implies statement (3). So it remains to prove statement (2) implies statement (1) and statement (3) implies statement (2). To show statement (2) implies statement (1), we use Tao’s result as a starting point, which states that the logarithmic Sarnak conjecture is equivalent to a conjecture involving the limit of averages on nilmanifolds, see Conjecture 2.1. By assuming that Conjecture 2.1 fails, we are able then to construct a system with polynomial mean complexity which does not satisfy the logarithmic Sarnak conjecture, and hence prove that statement (2) implies statement (1). To construct the system, we need to work on nilsystems and figure out the complexity of polynomial sequences, see Proposition 2.5. Precisely, we will show that for a given
![]() $\epsilon>0$
, for any
$\epsilon>0$
, for any
![]() $n\in \mathbb {N}$
, the minimal number of
$n\in \mathbb {N}$
, the minimal number of
![]() $\epsilon $
-dense subsets of strings of lengths n of the set of all polynomial sequences on
$\epsilon $
-dense subsets of strings of lengths n of the set of all polynomial sequences on
![]() $G/\Gamma $
is bounded by a polynomial which is only dependent on
$G/\Gamma $
is bounded by a polynomial which is only dependent on
![]() $\epsilon $
and
$\epsilon $
and
![]() $G/\Gamma $
, where
$G/\Gamma $
, where
![]() $G/\Gamma $
is an s-step nilmanifold. With the help of this proposition, we finish the construction and thus show that statement (2) implies statement (1). To show statement (3) implies statement (2), we study a t.d.s. with the small boundary property which was introduced by Lindenstrauss when studying mean dimension. Proposition 2.10 plays a key role for the proof, which states that for a t.d.s.
$G/\Gamma $
is an s-step nilmanifold. With the help of this proposition, we finish the construction and thus show that statement (2) implies statement (1). To show statement (3) implies statement (2), we study a t.d.s. with the small boundary property which was introduced by Lindenstrauss when studying mean dimension. Proposition 2.10 plays a key role for the proof, which states that for a t.d.s.
![]() $(X,T)$
with polynomial mean complexity and a subset U with small boundary, each
$(X,T)$
with polynomial mean complexity and a subset U with small boundary, each
![]() $x\in X$
is associated with a point in the shift space such that the complexity of the closure of the associated points is less than or equal to that of
$x\in X$
is associated with a point in the shift space such that the complexity of the closure of the associated points is less than or equal to that of
![]() $(X,T)$
. The result of Lindenstrauss and Weiss guarantees that if
$(X,T)$
. The result of Lindenstrauss and Weiss guarantees that if
![]() $(X,T)$
has zero entropy, then the product of X with any irrational rotation on the circle has the small boundary property. By using Proposition 2.10 and some simple argument, we finish the proof that statement (3) implies statement (2), and hence the proof of Theorem 1.1.
$(X,T)$
has zero entropy, then the product of X with any irrational rotation on the circle has the small boundary property. By using Proposition 2.10 and some simple argument, we finish the proof that statement (3) implies statement (2), and hence the proof of Theorem 1.1.
While Theorem 1.1 does not provide a proof of the logarithmic Sarnak conjecture directly, it does indicate that a t.d.s. with polynomial mean complexity is important for the proof of the conjecture. So, it will be useful to understand the structure of a subshift with polynomial mean complexity. We remark that we do not know if the polynomial mean complexity for a subshift can be replaced by the polynomial block-complexity in Theorem 1.1, which is extensively studied in the literature.
For a t.d.s.
![]() $(X,T)$
with a metric d,
$(X,T)$
with a metric d,
![]() $\epsilon>0$
, and a
$\epsilon>0$
, and a
![]() $\rho \in {\mathcal {M}}(X,T)$
, we let
$\rho \in {\mathcal {M}}(X,T)$
, we let
 $$ \begin{align*}&S_n(d,T,\rho,\epsilon)\\&\quad=\min \bigg\{ m\in \mathbb{N}:\text{there exists } x_1,x_2,\ldots,x_m \text{ s.t. } \rho\bigg(\bigcup_{i=1}^m B_{\overline{d}_n}(x_i,\epsilon)\bigg)>1-\epsilon\bigg\}.\end{align*} $$
$$ \begin{align*}&S_n(d,T,\rho,\epsilon)\\&\quad=\min \bigg\{ m\in \mathbb{N}:\text{there exists } x_1,x_2,\ldots,x_m \text{ s.t. } \rho\bigg(\bigcup_{i=1}^m B_{\overline{d}_n}(x_i,\epsilon)\bigg)>1-\epsilon\bigg\}.\end{align*} $$
It is clear that
![]() $S_n(d,T,\rho ,\epsilon )\le S_n(d, T,X ,\epsilon )$
for any
$S_n(d,T,\rho ,\epsilon )\le S_n(d, T,X ,\epsilon )$
for any
![]() $\rho \in {\mathcal {M}}(X,T)$
and
$\rho \in {\mathcal {M}}(X,T)$
and
![]() $\epsilon>0$
. We say a
$\epsilon>0$
. We say a
![]() $\rho \in {\mathcal {M}}(X,T)$
has sub-linear mean measure complexity if for any
$\rho \in {\mathcal {M}}(X,T)$
has sub-linear mean measure complexity if for any
![]() $\epsilon>0$
,
$\epsilon>0$
,
We say
![]() $(X,T)$
has sub-linear mean measure complexity if equation (1.4) holds for any
$(X,T)$
has sub-linear mean measure complexity if equation (1.4) holds for any
![]() $\rho \in {\mathcal {M}}(X,T)$
. We emphasize that the sub-linear mean measure complexity is an invariant in the measure-theoretic category. One can refer to [Reference Huang, Wang and Ye11, Proposition 2.2] for details.
$\rho \in {\mathcal {M}}(X,T)$
. We emphasize that the sub-linear mean measure complexity is an invariant in the measure-theoretic category. One can refer to [Reference Huang, Wang and Ye11, Proposition 2.2] for details.
By using the fact that the two-term logarithmic Chowla conjecture holds [Reference Tao21], that is,
 $$ \begin{align}\lim_{N\rightarrow \infty}\frac{1}{\ln N}\sum_{n=1}^{N}\frac{\mu(n+h_1)\mu(n+h_2)}{n}=0 \end{align} $$
$$ \begin{align}\lim_{N\rightarrow \infty}\frac{1}{\ln N}\sum_{n=1}^{N}\frac{\mu(n+h_1)\mu(n+h_2)}{n}=0 \end{align} $$
for any
![]() $0\le h_1<h_2\in \mathbb {N}$
, and by using the method of the proof of Theorem 1.1 in [Reference Huang, Wang and Ye11], we have the following theorem.
$0\le h_1<h_2\in \mathbb {N}$
, and by using the method of the proof of Theorem 1.1 in [Reference Huang, Wang and Ye11], we have the following theorem.
Theorem 1.2. The logarithmic Sarnak conjecture holds for any t.d.s. with sub-linear mean measure complexity. Consequently, the conjecture holds for any t.d.s. with sub-linear mean complexity.
We remark that, at this moment, we are not able to show that the logarithmic Sarnak conjecture holds for any t.d.s. with linear mean (measure) complexity. We also remark that if for any
![]() $k\in \mathbb {N}$
the
$k\in \mathbb {N}$
the
![]() $2k$
-term logarithmic Chowla conjecture holds, that is,
$2k$
-term logarithmic Chowla conjecture holds, that is,
 $$ \begin{align}\lim_{N\rightarrow \infty}\frac{1}{\ln N}\sum_{n=1}^{N}\frac{\mu(n+h_1)\mu(n+h_2)\ldots \mu(n+h_{2k})}{n}=0\end{align} $$
$$ \begin{align}\lim_{N\rightarrow \infty}\frac{1}{\ln N}\sum_{n=1}^{N}\frac{\mu(n+h_1)\mu(n+h_2)\ldots \mu(n+h_{2k})}{n}=0\end{align} $$
for any non-negative integer
![]() $0\le h_1\le h_2\le \cdots \le h_{2k}$
with an odd number
$0\le h_1\le h_2\le \cdots \le h_{2k}$
with an odd number
![]() $j\in \{1,2,\ldots ,2k\}$
such that
$j\in \{1,2,\ldots ,2k\}$
such that
![]() $h_j<h_{j+1}$
, then the logarithmic Sarnak conjecture holds for any t.d.s. with sub-polynomial (leading term
$h_j<h_{j+1}$
, then the logarithmic Sarnak conjecture holds for any t.d.s. with sub-polynomial (leading term
![]() $cn^k$
) mean measure complexity by using the method of Theorem 1.2. Thus, by Theorem 1.1, we know that the logarithmic Sarnak conjecture holds if the logarithmic Chowla conjecture holds. In fact, the two conjectures are equivalent [Reference Tao21].
$cn^k$
) mean measure complexity by using the method of Theorem 1.2. Thus, by Theorem 1.1, we know that the logarithmic Sarnak conjecture holds if the logarithmic Chowla conjecture holds. In fact, the two conjectures are equivalent [Reference Tao21].
As an application of Theorem 1.2, one has the following result.
Theorem 1.3. Let C be a non-empty compact subset of
![]() $[0,1]$
with packing dimension
$[0,1]$
with packing dimension
![]() $<1$
. Then
$<1$
. Then
where
![]() $e(t):=e^{2\pi i t}$
for any
$e(t):=e^{2\pi i t}$
for any
![]() $t\in \mathbb {R}$
.
$t\in \mathbb {R}$
.
We remark that in [Reference McNamara18, Theorem 1.13], McNamara proved that equation (1.7) holds for a non-empty compact subset C of
![]() $[0,1]$
with upper box dimension
$[0,1]$
with upper box dimension
![]() $< 1$
. So Theorem 1.3 strengthens the result in [Reference McNamara18].
$< 1$
. So Theorem 1.3 strengthens the result in [Reference McNamara18].
We say a t.d.s.
![]() $(X,T)$
has sub-polynomial mean measure complexity if for any
$(X,T)$
has sub-polynomial mean measure complexity if for any
![]() $\tau>0$
and
$\tau>0$
and
![]() $\rho \in \mathcal {M}(X,T)$
,
$\rho \in \mathcal {M}(X,T)$
,
for any
![]() $\epsilon>0$
. In [Reference Huang, Wang and Ye11], Huang, Wang, and Ye showed that the Sarnak conjecture holds for any t.d.s. with sub-polynomial mean measure complexity. As an application of the above result in [Reference Huang, Wang and Ye11], one has the following result.
$\epsilon>0$
. In [Reference Huang, Wang and Ye11], Huang, Wang, and Ye showed that the Sarnak conjecture holds for any t.d.s. with sub-polynomial mean measure complexity. As an application of the above result in [Reference Huang, Wang and Ye11], one has the following result.
Theorem 1.4. Let C be a non-empty compact subset of
![]() $[0,1]$
with packing dimension
$[0,1]$
with packing dimension
![]() $=0$
. Then,
$=0$
. Then,
The paper is organized as follows. In §2, we prove Theorem 1.1. In §3, we prove Theorem 1.3. In Appendixes A and B, we prove Theorems 1.2 and 1.4.
2 Proof of Theorem 1.1
In this section, we prove Theorem 1.1. As we said in the introduction, it remains to prove
![]() $(2)\Longrightarrow (1)$
which is done in §2.1, and
$(2)\Longrightarrow (1)$
which is done in §2.1, and
![]() $(3)\Longrightarrow (2)$
which is carried out in §2.2.
$(3)\Longrightarrow (2)$
which is carried out in §2.2.
2.1 Proof of statement (2) implies statement (1) in Theorem 1.1
We have explained in the introduction that the starting point of the proof is Tao’s result which gives an equivalent statement of the logarithmic Sarnak conjecture. We will first introduce the result, then derive some result concerning the complexity of polynomial sequences, and finally give the proof. Let us begin with basic notions related to nilmanifolds.
Let G be a group. For
![]() $g, h\in G$
, we write
$g, h\in G$
, we write
![]() $[g, h] = ghg^{-1}h^{-1}$
for the commutator of g and h, and we write
$[g, h] = ghg^{-1}h^{-1}$
for the commutator of g and h, and we write
![]() $[A,B]$
for the subgroup spanned by
$[A,B]$
for the subgroup spanned by
![]() $\{[a, b] : a \in A, b\in B\}$
. The commutator subgroups
$\{[a, b] : a \in A, b\in B\}$
. The commutator subgroups
![]() $G_j$
,
$G_j$
,
![]() $j\ge 1$
, are defined inductively by setting
$j\ge 1$
, are defined inductively by setting
![]() $G_1 = G$
and
$G_1 = G$
and
![]() $G_{j+1} = [G_j ,G]$
. Let
$G_{j+1} = [G_j ,G]$
. Let
![]() $s \ge 1$
be an integer. We say that G is s-step nilpotent if
$s \ge 1$
be an integer. We say that G is s-step nilpotent if
![]() $G_{s+1}$
is the trivial subgroup.
$G_{s+1}$
is the trivial subgroup.
Recall that an s-step nilmanifold is a manifold of the form
![]() $G/\Gamma $
, where G is a connected, simply connected s-step nilpotent Lie group, and
$G/\Gamma $
, where G is a connected, simply connected s-step nilpotent Lie group, and
![]() $\Gamma $
is a cocompact discrete subgroup of G. Tao shows that the logarithmic Sarnak conjecture is equivalent to the following conjecture [Reference Tao22].
$\Gamma $
is a cocompact discrete subgroup of G. Tao shows that the logarithmic Sarnak conjecture is equivalent to the following conjecture [Reference Tao22].
Conjecture 2.1. For any
![]() $s\in \mathbb {N}$
, an s-step nilmanifold
$s\in \mathbb {N}$
, an s-step nilmanifold
![]() $G/\Gamma $
, a
$G/\Gamma $
, a
![]() $\mathrm{Lip}$
-continuous function
$\mathrm{Lip}$
-continuous function
![]() $F:G/\Gamma \to \mathbb {C}$
, and
$F:G/\Gamma \to \mathbb {C}$
, and
![]() $x_0\in G/\Gamma $
, one has
$x_0\in G/\Gamma $
, one has
Let
![]() $G/\Gamma $
be an m-dimensional nilmanifold (that is, G is a connected, simply connected s-step nilpotent Lie group with unit element e and
$G/\Gamma $
be an m-dimensional nilmanifold (that is, G is a connected, simply connected s-step nilpotent Lie group with unit element e and
![]() $\Gamma $
is a cocompact discrete subgroup of G) and let
$\Gamma $
is a cocompact discrete subgroup of G) and let
![]() $G=G_1\supset \cdots \supset G_s\supset G_{s+1}=\{e\}$
be the lower central series filtration. We will make use of the Lie algebra
$G=G_1\supset \cdots \supset G_s\supset G_{s+1}=\{e\}$
be the lower central series filtration. We will make use of the Lie algebra
![]() $\mathfrak {g}$
over
$\mathfrak {g}$
over
![]() $\mathbb {R}$
of G together with the exponential map
$\mathbb {R}$
of G together with the exponential map
![]() $\exp : \mathfrak {g}\rightarrow G$
. Since G is a connected, simply connected s-step nilpotent Lie group, the exponential map is a diffeomorphism [Reference Corwin and Greenleaf1, Reference McNamara18]. A basis
$\exp : \mathfrak {g}\rightarrow G$
. Since G is a connected, simply connected s-step nilpotent Lie group, the exponential map is a diffeomorphism [Reference Corwin and Greenleaf1, Reference McNamara18]. A basis
![]() $\mathcal {X}= \{X_1, \ldots ,X_m\}$
for the Lie algebra
$\mathcal {X}= \{X_1, \ldots ,X_m\}$
for the Lie algebra
![]() $\mathfrak {g}$
over
$\mathfrak {g}$
over
![]() $\mathbb {R}$
is called a Mal’cev basis for
$\mathbb {R}$
is called a Mal’cev basis for
![]() $G/\Gamma $
if the following four conditions are satisfied.
$G/\Gamma $
if the following four conditions are satisfied.
-
(1) For each
 $j = 0,\ldots ,m-1$
, the subspace
$j = 0,\ldots ,m-1$
, the subspace
 $\eta _j := \text {Span}(X_{j+1}, \ldots ,X_m)$
is a Lie algebra ideal in
$\eta _j := \text {Span}(X_{j+1}, \ldots ,X_m)$
is a Lie algebra ideal in
 $\mathfrak {g}$
, and hence
$\mathfrak {g}$
, and hence
 $H_j := \exp \ \eta _j$
is a normal Lie subgroup of G.
$H_j := \exp \ \eta _j$
is a normal Lie subgroup of G. -
(2) For every
 $0< i\le s$
, there is
$0< i\le s$
, there is
 $l_{i-1}$
such that
$l_{i-1}$
such that
 $G_i = H_{l_{i-1}}$
. Thus,
$G_i = H_{l_{i-1}}$
. Thus,
 $0=l_0<l_1<\cdots <l_{s-1}\le m-1$
.
$0=l_0<l_1<\cdots <l_{s-1}\le m-1$
. -
(3) Each
 $g\in G$
can be written uniquely as
$g\in G$
can be written uniquely as
 $\exp (t_1X_1) \exp (t_2X_2)\ldots \exp (t_mX_m)$
for some
$\exp (t_1X_1) \exp (t_2X_2)\ldots \exp (t_mX_m)$
for some
 $t_i\in \mathbb {R}$
.
$t_i\in \mathbb {R}$
. -
(4)
 $\Gamma $
consists precisely of those elements which, when written in the above form, have all
$\Gamma $
consists precisely of those elements which, when written in the above form, have all
 $t_i\in \mathbb {Z}$
.
$t_i\in \mathbb {Z}$
.
Note that such a basis exists [Reference Corwin and Greenleaf1, Reference Green and Tao8, Reference Malcev16]. Now we fix a Mal’cev basis
![]() $\mathcal {X}= \{X_1, \ldots ,X_m\}$
of
$\mathcal {X}= \{X_1, \ldots ,X_m\}$
of
![]() $G/\Gamma $
. Define
$G/\Gamma $
. Define
![]() $\psi : G\rightarrow \mathbb {R}^m$
such that if
$\psi : G\rightarrow \mathbb {R}^m$
such that if
![]() $g=\exp (t_1X_1)\ldots \exp (t_mX_m)\in G$
, then
$g=\exp (t_1X_1)\ldots \exp (t_mX_m)\in G$
, then
Moreover, let
![]() $|\psi (g)|=\max _{1\le i\le m}|t_i|$
. The following metrics on G and
$|\psi (g)|=\max _{1\le i\le m}|t_i|$
. The following metrics on G and
![]() $G/\Gamma $
are introduced in [Reference Green and Tao8].
$G/\Gamma $
are introduced in [Reference Green and Tao8].
Definition 2.2. We define
![]() $d: G \times G\rightarrow \mathbb {R}$
to be the largest metric such that
$d: G \times G\rightarrow \mathbb {R}$
to be the largest metric such that
![]() $d(x, y)\le |\psi (xy^{-1})|$
for all
$d(x, y)\le |\psi (xy^{-1})|$
for all
![]() $x, y\in G$
. More explicitly, we have
$x, y\in G$
. More explicitly, we have
 $$ \begin{align*}d(x, y) = \inf\left\{\sum_{i=1}^n\min\{|\psi(x_{i-1}x_i^{-1})|, |\psi(x_ix_{i-1}^{-1})|\}: x_0,\ldots, x_n\in G; x_0=x,x_n=y\right\}\hspace{-2pt}.\end{align*} $$
$$ \begin{align*}d(x, y) = \inf\left\{\sum_{i=1}^n\min\{|\psi(x_{i-1}x_i^{-1})|, |\psi(x_ix_{i-1}^{-1})|\}: x_0,\ldots, x_n\in G; x_0=x,x_n=y\right\}\hspace{-2pt}.\end{align*} $$
This descends to a metric on
![]() $G/\Gamma $
by setting
$G/\Gamma $
by setting
It turns out that this is indeed a metric on
![]() $G/\Gamma $
(see [Reference Green and Tao8]). Since d is right-invariant (that is,
$G/\Gamma $
(see [Reference Green and Tao8]). Since d is right-invariant (that is,
![]() $d(x,y)=d(xg,yg)$
for all
$d(x,y)=d(xg,yg)$
for all
![]() $x,y,g\in G$
), we also have
$x,y,g\in G$
), we also have
The following lemma appears in [Reference Dong, Donoso, Maass, Shao and Ye3, Lemmas 7.5 and 7.6].
Lemma 2.3. Let G be a connected, simply connected s-step nilpotent Lie group. Then there exist real polynomials
![]() $P_1:\mathbb {R}^3\rightarrow \mathbb {R}$
,
$P_1:\mathbb {R}^3\rightarrow \mathbb {R}$
,
![]() $P_2:\mathbb {R}\rightarrow \mathbb {R}$
, and
$P_2:\mathbb {R}\rightarrow \mathbb {R}$
, and
![]() $P_3:\mathbb {R}^2\rightarrow \mathbb {R}$
with positive coefficients such that for
$P_3:\mathbb {R}^2\rightarrow \mathbb {R}$
with positive coefficients such that for
![]() $x,y,g,h\in G$
:
$x,y,g,h\in G$
:
-
(1)
 $d(gx,gy)\le P_1(|\psi (g)|,|\psi (x)|,|\psi (y)|)d(x,y)$
;
$d(gx,gy)\le P_1(|\psi (g)|,|\psi (x)|,|\psi (y)|)d(x,y)$
; -
(2)
 $|\psi (g^n)|\le P_2(n)|\psi (g)|^{n_G}$
, where
$|\psi (g^n)|\le P_2(n)|\psi (g)|^{n_G}$
, where
 $n_G$
is a positive constant determined by G;
$n_G$
is a positive constant determined by G; -
(3)
 $|\psi (gh)|\le P_3(|\psi (g)|,|\psi (h)|)$
.
$|\psi (gh)|\le P_3(|\psi (g)|,|\psi (h)|)$
.
Let G be a connected, simply connected s-step nilpotent Lie group with unit element e and
![]() $G= G_0= G_1$
,
$G= G_0= G_1$
,
![]() $G_{i+1}=[G,G_i]$
be the lower central series filtration of G. It is clear that
$G_{i+1}=[G,G_i]$
be the lower central series filtration of G. It is clear that
![]() $\{e\}=G_{s+1}=G_{s+2}=\cdots $
. By a polynomial sequence adapted to the lower central series filtration, we mean a map
$\{e\}=G_{s+1}=G_{s+2}=\cdots $
. By a polynomial sequence adapted to the lower central series filtration, we mean a map
![]() $\mathbf {g} : \mathbb {Z}\to G$
such that
$\mathbf {g} : \mathbb {Z}\to G$
such that
![]() $\partial _{h_i},\ldots, \partial _{h_1} {\mathbf {g}}\in G_i$
for all
$\partial _{h_i},\ldots, \partial _{h_1} {\mathbf {g}}\in G_i$
for all
![]() $i>0$
and
$i>0$
and
![]() $h_1,\ldots ,h_i\in \mathbb {Z}$
, where
$h_1,\ldots ,h_i\in \mathbb {Z}$
, where
for any map
![]() $\mathbf {f} : \mathbb {Z}\to G$
and
$\mathbf {f} : \mathbb {Z}\to G$
and
![]() $n,h\in \mathbb {Z}$
. Let
$n,h\in \mathbb {Z}$
. Let
![]() $\mathrm{Poly}(G)$
be the collection of all polynomial sequences of G adapted to the lower central series filtration. It is well known that a polynomial sequence
$\mathrm{Poly}(G)$
be the collection of all polynomial sequences of G adapted to the lower central series filtration. It is well known that a polynomial sequence
![]() ${\mathbf {g}} : \mathbb {Z}\to G$
adapted to the lower central series filtration has unique Taylor coefficients
${\mathbf {g}} : \mathbb {Z}\to G$
adapted to the lower central series filtration has unique Taylor coefficients
![]() $g_j \in G_j$
for each
$g_j \in G_j$
for each
![]() $0\le j \le s$
such that
$0\le j \le s$
such that
where
![]() $\tbinom {n}{0}\equiv 1$
(see for example [Reference Green, Tao and Ziegler9, Lemma B.9] and [Reference Host and Kra10, p. 240, Theorem 8]). In this case, we say that
$\tbinom {n}{0}\equiv 1$
(see for example [Reference Green, Tao and Ziegler9, Lemma B.9] and [Reference Host and Kra10, p. 240, Theorem 8]). In this case, we say that
![]() $g_i\in G_i$
for
$g_i\in G_i$
for
![]() $i=0,1,\ldots ,s$
is the coefficients of
$i=0,1,\ldots ,s$
is the coefficients of
![]() ${\mathbf {g}}$
.
${\mathbf {g}}$
.
Using Lemma 2.3(2) and (3), it is not hard to verify by induction that there exists a real polynomial
![]() $Q:\mathbb {R}^{s+2}\rightarrow \mathbb {R}$
with positive coefficients such that
$Q:\mathbb {R}^{s+2}\rightarrow \mathbb {R}$
with positive coefficients such that
for
![]() $n\in \mathbb {Z}_+$
.
$n\in \mathbb {Z}_+$
.
We note that for
![]() $g,h\in G$
,
$g,h\in G$
,
![]() ${\mathbf {g}} : \mathbb {Z}\to G$
defined by
${\mathbf {g}} : \mathbb {Z}\to G$
defined by
![]() ${\mathbf {g}}(n)=g^nh$
for each
${\mathbf {g}}(n)=g^nh$
for each
![]() $n\in \mathbb {N}$
is a polynomial sequence adapted to the lower central series filtration since
$n\in \mathbb {N}$
is a polynomial sequence adapted to the lower central series filtration since
For a non-empty subset K of G, we say
![]() ${\mathbf {g}}\in \mathrm{Poly}(G)$
a polynomial sequence with coefficients in K, if
${\mathbf {g}}\in \mathrm{Poly}(G)$
a polynomial sequence with coefficients in K, if
![]() $g_i\in G_i\cap K$
for
$g_i\in G_i\cap K$
for
![]() $i=0,1,\ldots , s$
, where
$i=0,1,\ldots , s$
, where
![]() $\{g_i\}_{i=0}^s$
are the coefficients of
$\{g_i\}_{i=0}^s$
are the coefficients of
![]() ${\mathbf {g}}$
. Green, Tao, and Ziegler proved the following lemma (see [Reference Green, Tao and Ziegler9, Lemma C.1] and [Reference Host and Kra10, p. 243, Proposition 12]).
${\mathbf {g}}$
. Green, Tao, and Ziegler proved the following lemma (see [Reference Green, Tao and Ziegler9, Lemma C.1] and [Reference Host and Kra10, p. 243, Proposition 12]).
Lemma 2.4. Let G be a connected, simply connected s-step nilpotent Lie group and
![]() $\Gamma $
be a cocompact discrete subgroup of G. Then there exists a compact subset K of G such that any polynomial sequence
$\Gamma $
be a cocompact discrete subgroup of G. Then there exists a compact subset K of G such that any polynomial sequence
![]() $\mathbf { g}\in \mathrm{Poly}(G)$
can be factorized as
$\mathbf { g}\in \mathrm{Poly}(G)$
can be factorized as
![]() ${\mathbf {g}}={\mathbf {g}}'\mathbf {\gamma }$
, where
${\mathbf {g}}={\mathbf {g}}'\mathbf {\gamma }$
, where
![]() ${\mathbf {g}}'\in \mathrm{Poly}(G)$
is a polynomial sequence with coefficients in K and
${\mathbf {g}}'\in \mathrm{Poly}(G)$
is a polynomial sequence with coefficients in K and
![]() $\mathbf {\gamma }\in \mathrm{Poly}(G)$
is a polynomial sequence with coefficients in
$\mathbf {\gamma }\in \mathrm{Poly}(G)$
is a polynomial sequence with coefficients in
![]() $\Gamma $
.
$\Gamma $
.
Let X be a separable metric space with metric d and Y be a non-empty subset of
![]() $X^{\mathbb {Z}}$
. For any
$X^{\mathbb {Z}}$
. For any
![]() $\epsilon>0$
, we let
$\epsilon>0$
, we let
![]() $s_n(Y,\epsilon )$
be the minimal number such that there exist
$s_n(Y,\epsilon )$
be the minimal number such that there exist
![]() $x_i\in Y,1\le i\le s_n(Y,\epsilon )$
satisfying that for any
$x_i\in Y,1\le i\le s_n(Y,\epsilon )$
satisfying that for any
![]() $y\in Y$
, there exists
$y\in Y$
, there exists
![]() $1\le i\le s_n(Y,\epsilon )$
with
$1\le i\le s_n(Y,\epsilon )$
with
![]() $d(x_i(k), y(k))<\epsilon $
for all
$d(x_i(k), y(k))<\epsilon $
for all
![]() $0\le k\le n-1$
. Roughly speaking,
$0\le k\le n-1$
. Roughly speaking,
![]() $s_n(Y,\epsilon )$
is the minimal number of points which are
$s_n(Y,\epsilon )$
is the minimal number of points which are
![]() $\epsilon $
-dense in
$\epsilon $
-dense in
![]() $Y[0,n-1]=\{(y_0,\ldots ,y_{n-1}): y=(y_i)_{i\in \mathbb {Z}}\in Y\}$
.
$Y[0,n-1]=\{(y_0,\ldots ,y_{n-1}): y=(y_i)_{i\in \mathbb {Z}}\in Y\}$
.
Let G be a connected, simply connected s-step nilpotent Lie group and
![]() $G/\Gamma $
be an s-step nilmanifold. For
$G/\Gamma $
be an s-step nilmanifold. For
![]() $K\subset G$
, let
$K\subset G$
, let
![]() $\mathrm{Poly}(K)$
be the collection of all polynomial sequences adapted to the lower central series filtration with coefficients in K. The map
$\mathrm{Poly}(K)$
be the collection of all polynomial sequences adapted to the lower central series filtration with coefficients in K. The map
![]() $\pi : \mathrm{Poly}(G) \to \{G/\Gamma \}^{\mathbb {Z}}$
is defined by
$\pi : \mathrm{Poly}(G) \to \{G/\Gamma \}^{\mathbb {Z}}$
is defined by
Put
![]() $\mathrm{Poly}(G/\Gamma )=\pi (\mathrm{Poly}(G))$
. We have the following.
$\mathrm{Poly}(G/\Gamma )=\pi (\mathrm{Poly}(G))$
. We have the following.
Proposition 2.5. Let
![]() $G/\Gamma $
be an s-step nilmanifold. Then there exists
$G/\Gamma $
be an s-step nilmanifold. Then there exists
![]() $k\in \mathbb {N}$
depending on
$k\in \mathbb {N}$
depending on
![]() $G/\Gamma $
such that for each
$G/\Gamma $
such that for each
![]() $\epsilon>0$
, we find
$\epsilon>0$
, we find
![]() $C(\epsilon )>0$
depending on
$C(\epsilon )>0$
depending on
![]() $G/\Gamma $
and k satisfying
$G/\Gamma $
and k satisfying
![]() $s_n(\mathrm{Poly}(G/\Gamma ),\epsilon )\le C(\epsilon )n^k$
for all
$s_n(\mathrm{Poly}(G/\Gamma ),\epsilon )\le C(\epsilon )n^k$
for all
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
To prove Proposition 2.5, we need the following lemma.
Lemma 2.6. Let G be a connected, simply connected s-step nilpotent Lie group and K be a non-empty compact subset of G. Then there is a real polynomial
![]() $P: \mathbb {R}\rightarrow \mathbb {R}$
depending on G and K such that
$P: \mathbb {R}\rightarrow \mathbb {R}$
depending on G and K such that
for any polynomials
![]() ${\mathbf {g}}(n)=g_0^{\tbinom {n}{0}}g_1^{\tbinom {n}{1}}\ldots g_s^{\tbinom {n}{s}}$
and
${\mathbf {g}}(n)=g_0^{\tbinom {n}{0}}g_1^{\tbinom {n}{1}}\ldots g_s^{\tbinom {n}{s}}$
and
![]() $\widetilde {\mathbf {g}}(n)=\widetilde g_0^{\tbinom {n}{0}} \widetilde g_1^{\tbinom {n}{1}}\ldots \widetilde g_s^{\tbinom {n}{s}}$
adapted to the lower central series filtration with coefficients
$\widetilde {\mathbf {g}}(n)=\widetilde g_0^{\tbinom {n}{0}} \widetilde g_1^{\tbinom {n}{1}}\ldots \widetilde g_s^{\tbinom {n}{s}}$
adapted to the lower central series filtration with coefficients
![]() $g_0,g_1,\ldots ,g_s,\widetilde g_0,\widetilde g_1,\ldots ,\widetilde g_s\in K$
.
$g_0,g_1,\ldots ,g_s,\widetilde g_0,\widetilde g_1,\ldots ,\widetilde g_s\in K$
.
Proof. Let
![]() $P_1,P_2,P_3$
be the real polynomials appearing in Lemma 2.3 and Q be the real polynomial appearing in equation (2.1). Since K is compact,
$P_1,P_2,P_3$
be the real polynomials appearing in Lemma 2.3 and Q be the real polynomial appearing in equation (2.1). Since K is compact,
![]() $w=\max \{|\psi (g)|:g\in K\}$
is a positive real number. Put
$w=\max \{|\psi (g)|:g\in K\}$
is a positive real number. Put
![]() $\widetilde Q(n)=Q(n,w,w,\ldots ,w)$
and
$\widetilde Q(n)=Q(n,w,w,\ldots ,w)$
and
![]() $\widetilde P_2(n)=w^{n_G}P_2(n)$
, where
$\widetilde P_2(n)=w^{n_G}P_2(n)$
, where
![]() $n_G$
is the constant appearing in Lemma 2.3(2).
$n_G$
is the constant appearing in Lemma 2.3(2).
Let
![]() ${\mathbf {g}}(n)=g_0^{\tbinom {n}{0}}g_1^{\tbinom {n}{1}}\ldots g_s^{\tbinom {n}{s}}$
and
${\mathbf {g}}(n)=g_0^{\tbinom {n}{0}}g_1^{\tbinom {n}{1}}\ldots g_s^{\tbinom {n}{s}}$
and
![]() $\widetilde {\mathbf {g}}(n)=\widetilde g_0^{\tbinom {n}{0}} \widetilde g_1^{\tbinom {n}{1}}\ldots \widetilde g_s^{\tbinom {n}{s}}$
be two polynomials adapted to the lower central series filtration with coefficients
$\widetilde {\mathbf {g}}(n)=\widetilde g_0^{\tbinom {n}{0}} \widetilde g_1^{\tbinom {n}{1}}\ldots \widetilde g_s^{\tbinom {n}{s}}$
be two polynomials adapted to the lower central series filtration with coefficients
![]() $g_0,\ldots ,g_s,\widetilde g_0,\ldots ,\widetilde g_s\in K$
. A simple computation yields
$g_0,\ldots ,g_s,\widetilde g_0,\ldots ,\widetilde g_s\in K$
. A simple computation yields
 $$ \begin{align} d({\mathbf{g}}(n),\widetilde {\mathbf{g}}(n))&\le \sum_{i=0}^{s-1}d\big(g_0^{\tbinom{n}{0}} \ldots g_{i-1}^{\tbinom{n}{i-1}}\widetilde g_{i}^{\tbinom{n}{i}}\ldots \widetilde g_s^{\tbinom{n}{s}},g_0^{\tbinom{n}{0}}\ldots g_{i}^{\tbinom{n}{i}} \widetilde g_{i+1}^{\tbinom{n}{i+1}}\ldots \widetilde g_s^{\tbinom{n}{s}}\big)\nonumber\\ &=\sum_{i=0}^{s-1}d\big(g_0^{\tbinom{n}{0}}\ldots g_{i-1}^{\tbinom{n}{i-1}} \widetilde g_{i}^{\tbinom{n}{i}},g_0^{\tbinom{n}{0}}\ldots g_{i}^{\tbinom{n}{i}}\big)\nonumber\\ &\le \sum_{i=0}^{s-1}P_1(|\psi(g_0^{\tbinom{n}{0}}\ldots g_{i-1}^{\tbinom{n}{i-1}})|, |\psi(\widetilde g_{i}^{\tbinom{n}{i}})|,|\psi(g_{i}^{\tbinom{n}{i}})|)d \big(\widetilde g_{i}^{\tbinom{n}{i}},g_{i}^{\tbinom{n}{i}}\big)\nonumber\\ &\le \sum_{i=0}^{s-1}P_1(\widetilde Q(n),\widetilde P_2(\tbinom{n}{i}), \widetilde P_2(\tbinom{n}{i}))d\big(\widetilde g_{i}^{\tbinom{n}{i}},g_{i}^{\tbinom{n}{i}}\big)\nonumber\\ &\le \widetilde P(n)\sum_{i=0}^{s-1}d\big(\widetilde g_{i}^{\tbinom{n}{i}},g_{i}^{\tbinom{n}{i}}\big) \end{align} $$
$$ \begin{align} d({\mathbf{g}}(n),\widetilde {\mathbf{g}}(n))&\le \sum_{i=0}^{s-1}d\big(g_0^{\tbinom{n}{0}} \ldots g_{i-1}^{\tbinom{n}{i-1}}\widetilde g_{i}^{\tbinom{n}{i}}\ldots \widetilde g_s^{\tbinom{n}{s}},g_0^{\tbinom{n}{0}}\ldots g_{i}^{\tbinom{n}{i}} \widetilde g_{i+1}^{\tbinom{n}{i+1}}\ldots \widetilde g_s^{\tbinom{n}{s}}\big)\nonumber\\ &=\sum_{i=0}^{s-1}d\big(g_0^{\tbinom{n}{0}}\ldots g_{i-1}^{\tbinom{n}{i-1}} \widetilde g_{i}^{\tbinom{n}{i}},g_0^{\tbinom{n}{0}}\ldots g_{i}^{\tbinom{n}{i}}\big)\nonumber\\ &\le \sum_{i=0}^{s-1}P_1(|\psi(g_0^{\tbinom{n}{0}}\ldots g_{i-1}^{\tbinom{n}{i-1}})|, |\psi(\widetilde g_{i}^{\tbinom{n}{i}})|,|\psi(g_{i}^{\tbinom{n}{i}})|)d \big(\widetilde g_{i}^{\tbinom{n}{i}},g_{i}^{\tbinom{n}{i}}\big)\nonumber\\ &\le \sum_{i=0}^{s-1}P_1(\widetilde Q(n),\widetilde P_2(\tbinom{n}{i}), \widetilde P_2(\tbinom{n}{i}))d\big(\widetilde g_{i}^{\tbinom{n}{i}},g_{i}^{\tbinom{n}{i}}\big)\nonumber\\ &\le \widetilde P(n)\sum_{i=0}^{s-1}d\big(\widetilde g_{i}^{\tbinom{n}{i}},g_{i}^{\tbinom{n}{i}}\big) \end{align} $$
for all
![]() $n\in \mathbb {N}$
, where
$n\in \mathbb {N}$
, where
![]() $\widetilde P(n)=\sum _{i=0}^{s-1}P_1(\widetilde Q(n),\widetilde P_2(\tbinom {n}{i}),\widetilde P_2(\tbinom {n}{i}))$
is a polynomial of n.
$\widetilde P(n)=\sum _{i=0}^{s-1}P_1(\widetilde Q(n),\widetilde P_2(\tbinom {n}{i}),\widetilde P_2(\tbinom {n}{i}))$
is a polynomial of n.
Now we are going to show that there is a real polynomial
![]() $P_4: \mathbb {R}\rightarrow \mathbb {R}$
such that
$P_4: \mathbb {R}\rightarrow \mathbb {R}$
such that
![]() $d(\widetilde g^{n},g^{n})\le P_4(n)d(\widetilde g,g)$
for all
$d(\widetilde g^{n},g^{n})\le P_4(n)d(\widetilde g,g)$
for all
![]() $g,\widetilde g\in K$
. In fact, it follows from the fact
$g,\widetilde g\in K$
. In fact, it follows from the fact
 $$ \begin{align}\begin{split} d(\widetilde g^{n},g^{n})&\le \sum_{i=0}^{n-1}d(\widetilde g^ig^{n-i},\widetilde g^{i+1}g^{n-i-1})=\sum_{i=0}^{n-1}d(\widetilde g^ig,\widetilde g^{i+1})\\ &\le\sum_{i=0}^{n-1}P_1(|\psi(\widetilde g^i)|,|\psi(\widetilde g)|,|\psi(g)|)d(\widetilde g,g)\\ &\le\sum_{i=0}^{n-1}P_1(\widetilde P_2(i),w,w)d(\widetilde g,g)\\ &\le P_4(n)d(\widetilde g,g) \end{split} \end{align} $$
$$ \begin{align}\begin{split} d(\widetilde g^{n},g^{n})&\le \sum_{i=0}^{n-1}d(\widetilde g^ig^{n-i},\widetilde g^{i+1}g^{n-i-1})=\sum_{i=0}^{n-1}d(\widetilde g^ig,\widetilde g^{i+1})\\ &\le\sum_{i=0}^{n-1}P_1(|\psi(\widetilde g^i)|,|\psi(\widetilde g)|,|\psi(g)|)d(\widetilde g,g)\\ &\le\sum_{i=0}^{n-1}P_1(\widetilde P_2(i),w,w)d(\widetilde g,g)\\ &\le P_4(n)d(\widetilde g,g) \end{split} \end{align} $$
for all
![]() $n\in \mathbb {N}$
, where
$n\in \mathbb {N}$
, where
![]() $P_4(n)=\sum _{i=0}^{n-1}P_1(\widetilde P_2(i),w,w)$
is a real polynomial of n. Summing up, we obtain
$P_4(n)=\sum _{i=0}^{n-1}P_1(\widetilde P_2(i),w,w)$
is a real polynomial of n. Summing up, we obtain
 $$ \begin{align*} d({\mathbf{g}}(n),\widetilde {\mathbf{g}}(n))&\overset{(2.2)}\le \widetilde P(n)\sum_{i=0}^{s-1}d\big(\widetilde g_{i}^{\tbinom{n}{i}},g_{i}^{\tbinom{n}{i}}\big)\\ &\overset{(2.3)}\le \widetilde P(n)\sum_{i=0}^{s-1}P_4(\tbinom{n}{i})d(\widetilde g_i,g_i)\\ &\le P(n)\max\{d(g_i,\widetilde g_i):0\le i\le s\} \end{align*} $$
$$ \begin{align*} d({\mathbf{g}}(n),\widetilde {\mathbf{g}}(n))&\overset{(2.2)}\le \widetilde P(n)\sum_{i=0}^{s-1}d\big(\widetilde g_{i}^{\tbinom{n}{i}},g_{i}^{\tbinom{n}{i}}\big)\\ &\overset{(2.3)}\le \widetilde P(n)\sum_{i=0}^{s-1}P_4(\tbinom{n}{i})d(\widetilde g_i,g_i)\\ &\le P(n)\max\{d(g_i,\widetilde g_i):0\le i\le s\} \end{align*} $$
for all
![]() $n\in \mathbb {N}$
, where
$n\in \mathbb {N}$
, where
![]() $P(n)=\widetilde P(n)\sum _{i=0}^{s-1}P_4(\tbinom {n}{i})$
is a real polynomial of n. Then
$P(n)=\widetilde P(n)\sum _{i=0}^{s-1}P_4(\tbinom {n}{i})$
is a real polynomial of n. Then
![]() $P(n)$
is the real polynomial as required. This ends the proof of Lemma 2.6.
$P(n)$
is the real polynomial as required. This ends the proof of Lemma 2.6.
Now we are ready to prove Proposition 2.5.
Proof of Proposition 2.5
By Lemma 2.4, there exists a compact subset K of G such that any polynomial sequence
![]() ${\mathbf {g}}$
adapted to the lower central series filtration can be factorized as
${\mathbf {g}}$
adapted to the lower central series filtration can be factorized as
![]() ${\mathbf {g}}={\mathbf {g}}'\mathbf {\gamma }$
, where
${\mathbf {g}}={\mathbf {g}}'\mathbf {\gamma }$
, where
![]() ${\mathbf {g}}'$
is a polynomial sequence adapted to the lower central series filtration with coefficients in K and
${\mathbf {g}}'$
is a polynomial sequence adapted to the lower central series filtration with coefficients in K and
![]() $\mathbf {\gamma }$
is a polynomial sequence with coefficients in
$\mathbf {\gamma }$
is a polynomial sequence with coefficients in
![]() $\Gamma $
. Since K is compact, by Lemma 2.6, there is a real polynomial
$\Gamma $
. Since K is compact, by Lemma 2.6, there is a real polynomial
![]() $P: \mathbb {R}\rightarrow \mathbb {R}$
such that
$P: \mathbb {R}\rightarrow \mathbb {R}$
such that
and any polynomials
![]() ${\mathbf {g}}$
,
${\mathbf {g}}$
,
![]() $\widetilde {\mathbf {g}}\in \mathrm{Poly}(G)$
with coefficients
$\widetilde {\mathbf {g}}\in \mathrm{Poly}(G)$
with coefficients
![]() $g_0,\ldots ,g_s,\widetilde g_0,\ldots ,\widetilde g_s\in K$
. It is not hard to see that there exists
$g_0,\ldots ,g_s,\widetilde g_0,\ldots ,\widetilde g_s\in K$
. It is not hard to see that there exists
![]() $k_0\in \mathbb {N}$
and
$k_0\in \mathbb {N}$
and
![]() $C>1$
such that
$C>1$
such that
Since K is compact, for
![]() $\epsilon> 0$
, we let
$\epsilon> 0$
, we let
![]() $N_\epsilon (K)$
be the smallest number of open balls of ratio
$N_\epsilon (K)$
be the smallest number of open balls of ratio
![]() $\epsilon $
needed to cover K. The upper Minkowski dimension or box dimension (see [Reference Mattila17]) is defined by
$\epsilon $
needed to cover K. The upper Minkowski dimension or box dimension (see [Reference Mattila17]) is defined by
This dimension of K is not larger than the usual dimension of G since K is a subset of G. Hence, there exists a positive constant L such that
 $$ \begin{align} N_\epsilon(K)\le L\bigg(\frac{1}{\min\{ \epsilon,1\}}\bigg)^{\mathrm{dim}(G)+1}. \end{align} $$
$$ \begin{align} N_\epsilon(K)\le L\bigg(\frac{1}{\min\{ \epsilon,1\}}\bigg)^{\mathrm{dim}(G)+1}. \end{align} $$
Set
 $$ \begin{align*}k=k_0(s+1)(\mathrm{dim}(G)+1)\quad\text{and}\quad C(\epsilon)=\bigg(L\bigg(\frac{2C}{\min\{ \epsilon,1\}}\bigg)^{\mathrm{dim}(G)+1}\bigg)^{s+1}\quad\text{for }\epsilon>0.\end{align*} $$
$$ \begin{align*}k=k_0(s+1)(\mathrm{dim}(G)+1)\quad\text{and}\quad C(\epsilon)=\bigg(L\bigg(\frac{2C}{\min\{ \epsilon,1\}}\bigg)^{\mathrm{dim}(G)+1}\bigg)^{s+1}\quad\text{for }\epsilon>0.\end{align*} $$
We are going to show that
for
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $\epsilon>0$
. To do this, let
$\epsilon>0$
. To do this, let
![]() $\pi $
be the projection from
$\pi $
be the projection from
![]() $\mathrm{Poly}(K)$
to
$\mathrm{Poly}(K)$
to
![]() $\mathrm{Poly}(G/\Gamma )$
defined by
$\mathrm{Poly}(G/\Gamma )$
defined by
![]() $\pi ({\mathbf {g}})(n)={\mathbf {g}}(n)\Gamma $
for all
$\pi ({\mathbf {g}})(n)={\mathbf {g}}(n)\Gamma $
for all
![]() $n\in \mathbb {Z}$
. By Lemma 2.4,
$n\in \mathbb {Z}$
. By Lemma 2.4,
![]() $\pi $
is surjective and
$\pi $
is surjective and
Hence,
For
![]() $\tau>0$
, we let
$\tau>0$
, we let
![]() $E_{\tau }$
be a finite subset of K such that
$E_{\tau }$
be a finite subset of K such that
 $$ \begin{align*} \sharp E_\tau\le N_{\tau}(K)\quad\text{and}\quad K\subset \bigcup_{g\in E_\tau}B(g,\tau). \end{align*} $$
$$ \begin{align*} \sharp E_\tau\le N_{\tau}(K)\quad\text{and}\quad K\subset \bigcup_{g\in E_\tau}B(g,\tau). \end{align*} $$
For
![]() $0\le i\le s$
, we let
$0\le i\le s$
, we let
![]() $E_{\tau }^{(i)}$
be a subset of
$E_{\tau }^{(i)}$
be a subset of
![]() $K\cap G_i$
such that
$K\cap G_i$
such that
 $$ \begin{align} \sharp E_\tau^{(i)}\le N_{\tau}(K)\quad\text{and}\quad K\cap G_i\subset \bigcup_{g\in E^i_\tau}B(g,2\tau). \end{align} $$
$$ \begin{align} \sharp E_\tau^{(i)}\le N_{\tau}(K)\quad\text{and}\quad K\cap G_i\subset \bigcup_{g\in E^i_\tau}B(g,2\tau). \end{align} $$
Put
![]() $P_\tau $
to be the collection of all polynomial sequences
$P_\tau $
to be the collection of all polynomial sequences
![]() ${\mathbf {g}}$
adapted to the lower central series filtration with coefficients
${\mathbf {g}}$
adapted to the lower central series filtration with coefficients
![]() $g_i\in E_\tau ^{(i)}$
,
$g_i\in E_\tau ^{(i)}$
,
![]() $i=0,1,\ldots ,s$
. Then for
$i=0,1,\ldots ,s$
. Then for
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $\epsilon>0$
,
$\epsilon>0$
,
 $$ \begin{align}\sharp P_{{\epsilon}/{2Cn^{k_0}}}= \prod_{i=0}^s\sharp E^{(i)}_{{\epsilon}/{2Cn^{k_0}}}\overset{(2.8),(2.6)} \le \left(L\left(\frac{2Cn^{k_0}}{\min\{ \epsilon,1\}}\right)^{\mathrm{dim}(G)+1}\right)^{s+1}=C(\epsilon)n^k. \end{align} $$
$$ \begin{align}\sharp P_{{\epsilon}/{2Cn^{k_0}}}= \prod_{i=0}^s\sharp E^{(i)}_{{\epsilon}/{2Cn^{k_0}}}\overset{(2.8),(2.6)} \le \left(L\left(\frac{2Cn^{k_0}}{\min\{ \epsilon,1\}}\right)^{\mathrm{dim}(G)+1}\right)^{s+1}=C(\epsilon)n^k. \end{align} $$
Now we fix
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $\epsilon>0$
. By equation (2.8), for any polynomial sequence
$\epsilon>0$
. By equation (2.8), for any polynomial sequence
![]() ${\mathbf {g}}\in \mathrm{Poly}(K)$
with coefficients
${\mathbf {g}}\in \mathrm{Poly}(K)$
with coefficients
![]() $g_0,\ldots ,g_s\in K$
, we have that
$g_0,\ldots ,g_s\in K$
, we have that
![]() $g_i\in K\cap G_i$
. Thus, there exists
$g_i\in K\cap G_i$
. Thus, there exists
![]() ${\bar {\mathbf g}}\in P_{{\epsilon }/{2Cn^{k_0}}}$
with coefficients
${\bar {\mathbf g}}\in P_{{\epsilon }/{2Cn^{k_0}}}$
with coefficients
![]() $\bar g_0\in E^{(0)}_{{\epsilon }/{2Cn^{k_0}}} ,\ldots ,\bar g_s\in E^{(s)}_{{\epsilon }/{2Cn^{k_0}}}$
such that
$\bar g_0\in E^{(0)}_{{\epsilon }/{2Cn^{k_0}}} ,\ldots ,\bar g_s\in E^{(s)}_{{\epsilon }/{2Cn^{k_0}}}$
such that
Therefore,
and for
![]() $1\le j\le n-1$
, one has
$1\le j\le n-1$
, one has
Hence,
Since the above inequality holds for all
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $\epsilon>0$
, we end the proof of Proposition 2.5.
$\epsilon>0$
, we end the proof of Proposition 2.5.
With the above preparations, now we are in the position to prove Theorem 1.1.
Proof of (2)
 $\Longrightarrow $
(1) in Theorem 1.1
$\Longrightarrow $
(1) in Theorem 1.1
Assume that Theorem 1.1(2) holds, that is, the logarithmic Sarnak conjecture holds for any t.d.s. with polynomial mean complexity. In what follows, we aim to show that the logarithmic Sarnak conjecture holds.
Assume the contrary that this is not the case, then by Tao’s result [Reference Tao22], the Conjecture 2.1 does not hold. This means that there exist an
![]() $s\in \mathbb {N}$
, an s-step nilmanifold
$s\in \mathbb {N}$
, an s-step nilmanifold
![]() $G/\Gamma $
, a
$G/\Gamma $
, a
![]() $\mathrm{Lip}$
-continuous function
$\mathrm{Lip}$
-continuous function
![]() $F:G/\Gamma \to \mathbb {C}$
, and an
$F:G/\Gamma \to \mathbb {C}$
, and an
![]() $x_0\in G/\Gamma $
such that
$x_0\in G/\Gamma $
such that
It is clear that
![]() $\|F\|_{\infty }:=\max _{x\in G/\Gamma }|F(x)|>0$
. Without loss of generality, we assume that
$\|F\|_{\infty }:=\max _{x\in G/\Gamma }|F(x)|>0$
. Without loss of generality, we assume that
Now we add an extra point p to the compact metric space
![]() $G/\Gamma $
. We then extend the metric d on
$G/\Gamma $
. We then extend the metric d on
![]() $G/\Gamma $
to the space
$G/\Gamma $
to the space
![]() $G/\Gamma \cup \{p\}$
by letting
$G/\Gamma \cup \{p\}$
by letting
![]() $d(p,x)=1$
for all
$d(p,x)=1$
for all
![]() $x\in G/\Gamma $
. So,
$x\in G/\Gamma $
. So,
![]() $(G/\Gamma \cup \{p\},d)$
is also a compact metric space. Let
$(G/\Gamma \cup \{p\},d)$
is also a compact metric space. Let
![]() $\widetilde F: (G/\Gamma \cup \{p\})^{\mathbb {Z}}\to \mathbb {C}$
be defined by
$\widetilde F: (G/\Gamma \cup \{p\})^{\mathbb {Z}}\to \mathbb {C}$
be defined by
![]() $\widetilde F(z)=F(z(0))$
if
$\widetilde F(z)=F(z(0))$
if
![]() $z(0)\in G/\Gamma $
and
$z(0)\in G/\Gamma $
and
![]() $0$
if
$0$
if
![]() $z(0)=p$
. It is clear that
$z(0)=p$
. It is clear that
![]() $\widetilde F$
is a continuous function and
$\widetilde F$
is a continuous function and
by equation (2.11).
In what follows, we will find a point
![]() $y\in (G/\Gamma \cup \{p\})^{\mathbb {Z}}$
such that
$y\in (G/\Gamma \cup \{p\})^{\mathbb {Z}}$
such that
and the t.d.s.
![]() $(X_y,\sigma )$
has polynomial mean complexity, where
$(X_y,\sigma )$
has polynomial mean complexity, where
![]() $\sigma : (G/\Gamma \cup \{p\})^{\mathbb {Z}}\rightarrow (G/\Gamma \cup \{p\})^{\mathbb {Z}}$
is the left shift and
$\sigma : (G/\Gamma \cup \{p\})^{\mathbb {Z}}\rightarrow (G/\Gamma \cup \{p\})^{\mathbb {Z}}$
is the left shift and
![]() $X_y=\overline {\{\sigma ^ny:n\in \mathbb {Z}\}}$
is a
$X_y=\overline {\{\sigma ^ny:n\in \mathbb {Z}\}}$
is a
![]() $\sigma $
-invariant compact subset of
$\sigma $
-invariant compact subset of
![]() $(G/\Gamma \cup \{p\})^{\mathbb {Z}}$
. Clearly, this is a contradiction to our assumption and thus proves that statement (2) implies statement (1) in Theorem 1.1.
$(G/\Gamma \cup \{p\})^{\mathbb {Z}}$
. Clearly, this is a contradiction to our assumption and thus proves that statement (2) implies statement (1) in Theorem 1.1.
We divide the remaining proof into two steps.
Step 1. The construction of the point y. First, we note that
 $$ \begin{align*}|z|\le \sum_{j=0}^{3} \max\bigg\{ \mathrm{Re}\bigg(e\bigg(\frac{j}{4}\bigg)z\bigg),0\bigg\}\end{align*} $$
$$ \begin{align*}|z|\le \sum_{j=0}^{3} \max\bigg\{ \mathrm{Re}\bigg(e\bigg(\frac{j}{4}\bigg)z\bigg),0\bigg\}\end{align*} $$
for
![]() $z\in \mathbb {C}$
. Thus, by equation (2.10), there is
$z\in \mathbb {C}$
. Thus, by equation (2.10), there is
![]() $\beta \in \{0,\tfrac 14,\tfrac 24,\tfrac 34\}$
such that
$\beta \in \{0,\tfrac 14,\tfrac 24,\tfrac 34\}$
such that
Thus, we can find
![]() $\tau \in (0,1)$
with
$\tau \in (0,1)$
with
is an infinite set. Moreover, putting
![]() and by induction, we can find strictly increasing sequences
and by induction, we can find strictly increasing sequences
![]() $\{H_i\}_{i=1}^{\infty }$
of E and
$\{H_i\}_{i=1}^{\infty }$
of E and
![]() $\{N_i\}_{i=1}^\infty $
of natural numbers such that for each
$\{N_i\}_{i=1}^\infty $
of natural numbers such that for each
![]() $i\in \mathbb {N}$
, one has
$i\in \mathbb {N}$
, one has
and there exist
![]() $g_{n,i}\in G$
for
$g_{n,i}\in G$
for
![]() $ 1\le n\le N_i$
satisfying
$ 1\le n\le N_i$
satisfying
For
![]() $i\in \mathbb {N}$
, let
$i\in \mathbb {N}$
, let
![]() $M_i=\sum _{n=1}^{N_i}({1}/{n})$
and
$M_i=\sum _{n=1}^{N_i}({1}/{n})$
and
 $$ \begin{align} S_i=\bigg\{n\in [1,N_i]\cap \mathbb{Z}: \mathrm{Re}(e(\beta)\mathbb{E}_{h\le H_i}\mu(n+h)F(g_{n,i}^hx_0))>\frac{\tau}{2}\bigg\}. \end{align} $$
$$ \begin{align} S_i=\bigg\{n\in [1,N_i]\cap \mathbb{Z}: \mathrm{Re}(e(\beta)\mathbb{E}_{h\le H_i}\mu(n+h)F(g_{n,i}^hx_0))>\frac{\tau}{2}\bigg\}. \end{align} $$
Then by equations (2.12) and (2.15), we have
 $$ \begin{align} \sum_{n\in S_i}\frac{1}{n}>\frac{\tau}{2}M_i. \end{align} $$
$$ \begin{align} \sum_{n\in S_i}\frac{1}{n}>\frac{\tau}{2}M_i. \end{align} $$
Notice that
![]() $\lim _{N\to +\infty }({\sum _{n\le N^\sigma }({1}/{n})}/{\sum _{n\le N}({1}/{n})})=\sigma .$
So, when
$\lim _{N\to +\infty }({\sum _{n\le N^\sigma }({1}/{n})}/{\sum _{n\le N}({1}/{n})})=\sigma .$
So, when
![]() $i\in \mathbb {N}$
is large enough, we have
$i\in \mathbb {N}$
is large enough, we have
 $$ \begin{align*}\sum_{n\in S_i\setminus[1, N_{i}^\sigma]}\frac{1}{n}\overset{(2.17)}>\frac{\tau}{2}M_i-\sum_{n\le N_{i}^\sigma}\frac{1}{n}>\frac{\tau}{2}M_i-2\sigma M_{i}>\frac{\tau}{4}M_i. \end{align*} $$
$$ \begin{align*}\sum_{n\in S_i\setminus[1, N_{i}^\sigma]}\frac{1}{n}\overset{(2.17)}>\frac{\tau}{2}M_i-\sum_{n\le N_{i}^\sigma}\frac{1}{n}>\frac{\tau}{2}M_i-2\sigma M_{i}>\frac{\tau}{4}M_i. \end{align*} $$
Hence, we can select
![]() $S_i'\subset S_i\setminus [1,N_{i}^\sigma ]$
with each gap not less than
$S_i'\subset S_i\setminus [1,N_{i}^\sigma ]$
with each gap not less than
![]() $2H_i$
and
$2H_i$
and
 $$ \begin{align} \sum_{n\in S^{\prime}_i}\frac{1}{n}> \frac{\tau M_i}{8H_i} \end{align} $$
$$ \begin{align} \sum_{n\in S^{\prime}_i}\frac{1}{n}> \frac{\tau M_i}{8H_i} \end{align} $$
for
![]() $i\in \mathbb {N}$
large enough.
$i\in \mathbb {N}$
large enough.
Define
![]() $y: \mathbb {Z}\to G/\Gamma \cup \{p\}$
such that
$y: \mathbb {Z}\to G/\Gamma \cup \{p\}$
such that
and
![]() $y(m)=p$
for
$y(m)=p$
for
![]() $m\in \mathbb {Z}\setminus \bigcup _{i=1}^{\infty } \bigcup _{n\in S_i'}\{n+1,n+2,\ldots , n+H_i\}$
.
$m\in \mathbb {Z}\setminus \bigcup _{i=1}^{\infty } \bigcup _{n\in S_i'}\{n+1,n+2,\ldots , n+H_i\}$
.
Clearly, y is well defined since
![]() $N_{i+1}>N_i+H_i$
by equation (2.14). Then one has by equations (2.16) and (2.18) that
$N_{i+1}>N_i+H_i$
by equation (2.14). Then one has by equations (2.16) and (2.18) that
 $$ \begin{align*} \mathrm{Re}\bigg(e(\beta)\sum_{n\in S_i'}\frac{1}{n}\sum_{h\le H_i}\mu(n+h)\widetilde F(\sigma^{n+h}y)\bigg)>\frac{\tau^2}{16}M_i \end{align*} $$
$$ \begin{align*} \mathrm{Re}\bigg(e(\beta)\sum_{n\in S_i'}\frac{1}{n}\sum_{h\le H_i}\mu(n+h)\widetilde F(\sigma^{n+h}y)\bigg)>\frac{\tau^2}{16}M_i \end{align*} $$
for
![]() $i\in \mathbb {N}$
large enough. This implies
$i\in \mathbb {N}$
large enough. This implies
 $$ \begin{align} \bigg|\sum_{n\in S_i'}\frac{1}{n}\sum_{h\le H_i}\mu(n+h)\widetilde F(\sigma^{n+h}y)\bigg|>\frac{\tau^2}{16}M_i \end{align} $$
$$ \begin{align} \bigg|\sum_{n\in S_i'}\frac{1}{n}\sum_{h\le H_i}\mu(n+h)\widetilde F(\sigma^{n+h}y)\bigg|>\frac{\tau^2}{16}M_i \end{align} $$
for
![]() $i\in \mathbb {N}$
large enough. Moreover, for
$i\in \mathbb {N}$
large enough. Moreover, for
![]() $i\in \mathbb {N}$
large enough,
$i\in \mathbb {N}$
large enough,
 $$ \begin{align*} \bigg|&\sum_{n\in S_i'}\frac{1}{n}\sum_{h\le H_i}\mu(n+h)\widetilde F(\sigma^{n+h}y)-\sum_{n\in S_i'} \sum_{h\le H_i}\frac{\mu(n+h)\widetilde F(\sigma^{n+h}y)}{n+h}\bigg|\\ &\overset{(2.12)}\le \sum_{n\in S_i'} \sum_{h\le H_i}\bigg(\frac{1}{n}-\frac{1}{n+h}\bigg)\le \sum_{n\in S_i'} \sum_{h\le H_i}\frac{H_i}{n(n+H_i)}\\ &\,\le \sum_{n\in S_i'} \frac{H_i}{n(N_i^\sigma+H_i)}\le \sum_{n\in S_i'} \frac{H_i}{nN_i^\sigma}\\ &\overset{(2.14)}\le \sigma\sum_{n\in S_i'}\frac{1}{n}\le \frac{\tau^2}{32}M_i. \end{align*} $$
$$ \begin{align*} \bigg|&\sum_{n\in S_i'}\frac{1}{n}\sum_{h\le H_i}\mu(n+h)\widetilde F(\sigma^{n+h}y)-\sum_{n\in S_i'} \sum_{h\le H_i}\frac{\mu(n+h)\widetilde F(\sigma^{n+h}y)}{n+h}\bigg|\\ &\overset{(2.12)}\le \sum_{n\in S_i'} \sum_{h\le H_i}\bigg(\frac{1}{n}-\frac{1}{n+h}\bigg)\le \sum_{n\in S_i'} \sum_{h\le H_i}\frac{H_i}{n(n+H_i)}\\ &\,\le \sum_{n\in S_i'} \frac{H_i}{n(N_i^\sigma+H_i)}\le \sum_{n\in S_i'} \frac{H_i}{nN_i^\sigma}\\ &\overset{(2.14)}\le \sigma\sum_{n\in S_i'}\frac{1}{n}\le \frac{\tau^2}{32}M_i. \end{align*} $$
Combining this inequality with equation (2.19), one has
 $$ \begin{align} \bigg|\sum_{N_{i}^\sigma<n \le N_i+H_i}\frac{\mu (n )\widetilde F(\sigma^{n}y)}{n}\bigg|=\bigg|\sum_{n\in S_i'} \sum_{h\le H_i}\frac{\mu(n+h)\widetilde F(\sigma^{n+h}y)}{n+h}\bigg|\ge \frac{\tau^2M_i}{32} \end{align} $$
$$ \begin{align} \bigg|\sum_{N_{i}^\sigma<n \le N_i+H_i}\frac{\mu (n )\widetilde F(\sigma^{n}y)}{n}\bigg|=\bigg|\sum_{n\in S_i'} \sum_{h\le H_i}\frac{\mu(n+h)\widetilde F(\sigma^{n+h}y)}{n+h}\bigg|\ge \frac{\tau^2M_i}{32} \end{align} $$
for
![]() $i\in \mathbb {N}$
large enough. Thus,
$i\in \mathbb {N}$
large enough. Thus,
 $$ \begin{align*} \bigg|&\frac{1}{M_i}\sum_{n\le N_i}\frac{\mu (n )\widetilde F(\sigma^{n}y)}{n}\bigg|\\&\,\ge\frac{1}{M_i} \bigg|\sum_{N_{i}^\sigma<n\le N_i+H_i}\frac{\mu (n )\widetilde F(\sigma^{n}y)}{n}\bigg| -\frac{1}{M_i}\sum_{n\le N_{i}^\sigma\text{ or}\atop N_i<n\le N_i+H_i}\bigg|\frac{\mu (n )\widetilde F(\sigma^{n}y)}{n}\bigg|\\&\overset{(2.20)}\ge\frac{\tau^2}{32}-\frac{\|\widetilde F\|_\infty}{M_i} \sum_{ N_i<n\le N_i+H_i}\frac{1}{n}-\frac{\|\widetilde F\|_\infty}{M_i}\sum_{ n\le N_{i}^\sigma}\frac{1}{n}\\&\overset{(2.12)}\ge\frac{\tau^2}{32}-\frac{H_i}{N_i}-2\sigma\overset{(2.14)}\ge \frac{\tau^2}{32}-3\sigma \overset{(2.14)}\ge \frac{\tau^2}{100} \end{align*} $$
$$ \begin{align*} \bigg|&\frac{1}{M_i}\sum_{n\le N_i}\frac{\mu (n )\widetilde F(\sigma^{n}y)}{n}\bigg|\\&\,\ge\frac{1}{M_i} \bigg|\sum_{N_{i}^\sigma<n\le N_i+H_i}\frac{\mu (n )\widetilde F(\sigma^{n}y)}{n}\bigg| -\frac{1}{M_i}\sum_{n\le N_{i}^\sigma\text{ or}\atop N_i<n\le N_i+H_i}\bigg|\frac{\mu (n )\widetilde F(\sigma^{n}y)}{n}\bigg|\\&\overset{(2.20)}\ge\frac{\tau^2}{32}-\frac{\|\widetilde F\|_\infty}{M_i} \sum_{ N_i<n\le N_i+H_i}\frac{1}{n}-\frac{\|\widetilde F\|_\infty}{M_i}\sum_{ n\le N_{i}^\sigma}\frac{1}{n}\\&\overset{(2.12)}\ge\frac{\tau^2}{32}-\frac{H_i}{N_i}-2\sigma\overset{(2.14)}\ge \frac{\tau^2}{32}-3\sigma \overset{(2.14)}\ge \frac{\tau^2}{100} \end{align*} $$
for
![]() $i\in \mathbb {N}$
large enough. This deduces that
$i\in \mathbb {N}$
large enough. This deduces that
 $$ \begin{align*}\limsup_{N\to\infty}|\mathbb{E}_{n\le N}^{\log} \mu (n)\widetilde F(\sigma^ny)|\ge \frac{\tau^2}{100}>0. \end{align*} $$
$$ \begin{align*}\limsup_{N\to\infty}|\mathbb{E}_{n\le N}^{\log} \mu (n)\widetilde F(\sigma^ny)|\ge \frac{\tau^2}{100}>0. \end{align*} $$
Therefore, y is the point as required.
Step 2.
![]() $(X_y,\sigma )$
has polynomial mean complexity. Recall that
$(X_y,\sigma )$
has polynomial mean complexity. Recall that
![]() $X_y =\overline {\{\sigma ^ny:n\in \mathbb {Z}\}}$
is a compact
$X_y =\overline {\{\sigma ^ny:n\in \mathbb {Z}\}}$
is a compact
![]() $\sigma $
-invariant subset of
$\sigma $
-invariant subset of
![]() $(G/\Gamma \cup \{p\})^{\mathbb {Z}}$
. The metric on
$(G/\Gamma \cup \{p\})^{\mathbb {Z}}$
. The metric on
![]() $(G/\Gamma \cup \{p\})^{\mathbb {Z}}$
is defined by
$(G/\Gamma \cup \{p\})^{\mathbb {Z}}$
is defined by
 $$ \begin{align}D(x,x')=\sum_{n\in\mathbb{Z}}\frac{d(x(n),x'(n))}{2^{|n|+2}}\end{align} $$
$$ \begin{align}D(x,x')=\sum_{n\in\mathbb{Z}}\frac{d(x(n),x'(n))}{2^{|n|+2}}\end{align} $$
for
![]() $x=(x(n))_{n\in \mathbb {Z}}, x'=(x'(n))_{n\in \mathbb {Z}}\in (G/\Gamma \cup \{p\})^{\mathbb {Z}}$
. By Proposition 2.5, we can find
$x=(x(n))_{n\in \mathbb {Z}}, x'=(x'(n))_{n\in \mathbb {Z}}\in (G/\Gamma \cup \{p\})^{\mathbb {Z}}$
. By Proposition 2.5, we can find
![]() $k>1$
such that
$k>1$
such that
Now we are going to show that
For
![]() $n\in \mathbb {Z}_+$
and
$n\in \mathbb {Z}_+$
and
![]() $-n\le q\le n$
, let
$-n\le q\le n$
, let
![]() $X_{n,q}$
be the collection of all points
$X_{n,q}$
be the collection of all points
![]() $z\in (G/\Gamma \cup \{p\})^{\mathbb {Z}}$
with
$z\in (G/\Gamma \cup \{p\})^{\mathbb {Z}}$
with
 $$ \begin{align*}z(j)=\begin{cases} p & \text{if }-n\le j< q, \\ {\mathbf{g}}(j)\Gamma & \text{if } q\le j\le n, \end{cases}\!\! \end{align*} $$
$$ \begin{align*}z(j)=\begin{cases} p & \text{if }-n\le j< q, \\ {\mathbf{g}}(j)\Gamma & \text{if } q\le j\le n, \end{cases}\!\! \end{align*} $$
where
![]() ${\mathbf {g}}$
is some polynomial sequence of G adapted to the lower central series filtration; and let
${\mathbf {g}}$
is some polynomial sequence of G adapted to the lower central series filtration; and let
![]() $X_{n,q}^*$
be the collection of all points
$X_{n,q}^*$
be the collection of all points
![]() $z\in (G/\Gamma \cup \{p\})^{\mathbb {Z}}$
with
$z\in (G/\Gamma \cup \{p\})^{\mathbb {Z}}$
with
 $$ \begin{align*}z(j)=\begin{cases} {\mathbf{g}}(j)\Gamma & \text{if }-n\le j< q, \\ p & \text{if } q\le j\le n, \end{cases}\!\! \end{align*} $$
$$ \begin{align*}z(j)=\begin{cases} {\mathbf{g}}(j)\Gamma & \text{if }-n\le j< q, \\ p & \text{if } q\le j\le n, \end{cases}\!\! \end{align*} $$
where
![]() ${\mathbf {g}}$
is some polynomial sequence of G adapted to the lower central series filtration.
${\mathbf {g}}$
is some polynomial sequence of G adapted to the lower central series filtration.
For
![]() $i\in \mathbb {N}$
, put
$i\in \mathbb {N}$
, put
![]() $t_i=[H_i/2]$
, where
$t_i=[H_i/2]$
, where
![]() $[u]$
is the integer part of the real number u. Then,
$[u]$
is the integer part of the real number u. Then,
In fact, since
![]() $H_{j+1}>N_j+H_j$
for all
$H_{j+1}>N_j+H_j$
for all
![]() $j\in \mathbb {N}$
, one has
$j\in \mathbb {N}$
, one has
by the construction of y. It is not hard to see that
![]() $X_{t_i,q},X_{t_i,q}^*$
are all compact subsets of
$X_{t_i,q},X_{t_i,q}^*$
are all compact subsets of
![]() $(G/\Gamma \cup \{p\})^{\mathbb {Z}}$
for each
$(G/\Gamma \cup \{p\})^{\mathbb {Z}}$
for each
![]() $-t_i\le q \le t_i$
and
$-t_i\le q \le t_i$
and
![]() $i\in \mathbb {N}$
by Lemma 2.4. Hence, the set in right part of equation (2.23) is also a compact subset of
$i\in \mathbb {N}$
by Lemma 2.4. Hence, the set in right part of equation (2.23) is also a compact subset of
![]() $(G/\Gamma \cup \{p\})^{\mathbb {Z}}$
. Now equation (2.23) follows from equation (2.24).
$(G/\Gamma \cup \{p\})^{\mathbb {Z}}$
. Now equation (2.23) follows from equation (2.24).
Now we fix
![]() $\epsilon>0$
. We have the following claim.
$\epsilon>0$
. We have the following claim.
Claim. For
![]() $i\in \mathbb {N}$
large enough, one has:
$i\in \mathbb {N}$
large enough, one has:
-
(1)
 $S_{[t_i/2]}(D,\sigma ,X_{t_i,q},\epsilon )\le s_{t_i}(\mathrm{Poly}(G/\Gamma ),{\epsilon }/{2})$
for all
$S_{[t_i/2]}(D,\sigma ,X_{t_i,q},\epsilon )\le s_{t_i}(\mathrm{Poly}(G/\Gamma ),{\epsilon }/{2})$
for all
 $q\in [-t_i,t_i]\cap \mathbb {Z}$
;
$q\in [-t_i,t_i]\cap \mathbb {Z}$
; -
(2)
 $S_{[t_i/2]}(D,\sigma ,X^*_{t_i,p},\epsilon )\le s_{t_i}(\mathrm{Poly}(G/\Gamma ),{\epsilon }/{2})$
for all
$S_{[t_i/2]}(D,\sigma ,X^*_{t_i,p},\epsilon )\le s_{t_i}(\mathrm{Poly}(G/\Gamma ),{\epsilon }/{2})$
for all
 $q\in [-t_i,t_i]\cap \mathbb {Z}$
.
$q\in [-t_i,t_i]\cap \mathbb {Z}$
.
Proof of the Claim
We prove part (1) first. For
![]() $i\in \mathbb {N}$
and
$i\in \mathbb {N}$
and
![]() $-t_i\le q\le t_i$
, we let
$-t_i\le q\le t_i$
, we let
![]() $\pi _{i,q}: \mathrm{Poly}(G/\Gamma )\to X_{t_i,q}$
be defined by
$\pi _{i,q}: \mathrm{Poly}(G/\Gamma )\to X_{t_i,q}$
be defined by
 $$ \begin{align*}\pi_{i,q}(z)(j)=\begin{cases} p & \text{ if }-t_i\le j<q,\\ z(j) & \text{ otherwise},\end{cases}\end{align*} $$
$$ \begin{align*}\pi_{i,q}(z)(j)=\begin{cases} p & \text{ if }-t_i\le j<q,\\ z(j) & \text{ otherwise},\end{cases}\end{align*} $$
for
![]() $z\in \mathrm{Poly}(G/\Gamma )$
. For
$z\in \mathrm{Poly}(G/\Gamma )$
. For
![]() $i\in \mathbb {N}$
large enough, if
$i\in \mathbb {N}$
large enough, if
![]() $z,\widetilde z\in \mathrm{Poly}(G/\Gamma )$
with
$z,\widetilde z\in \mathrm{Poly}(G/\Gamma )$
with
![]() $d(z(j),\widetilde z(j))<{\epsilon }/{2}$
for all
$d(z(j),\widetilde z(j))<{\epsilon }/{2}$
for all
![]() $-t_i\le j\le t_i$
, then for
$-t_i\le j\le t_i$
, then for
![]() $q\in [-t_i,t_i]\cap \mathbb {Z}$
,
$q\in [-t_i,t_i]\cap \mathbb {Z}$
,
 $$ \begin{align} &\!\!\bar{D}_{[t_i/2]}(\pi_{i,q}(z),\pi_{i,q}(\widetilde z))=\frac{1}{[t_i/2]}\sum_{l=0}^{[t_i/2]-1}D(\sigma^lz,\sigma^l\widetilde z)\nonumber\\ &\ \ \overset{(2.21)}= \frac{1}{[t_i/2]}\sum_{l=0}^{[t_i/2]-1}\sum_{n\in\mathbb{Z}}\frac{d(z(n+l),\widetilde z(n+l))}{2^{|n|+2}}\nonumber\\ &\quad\le \frac{1}{[t_i/2]}\sum_{l=0}^{[t_i/2]-1}\bigg(\sum_{|n|\le [t_i/2] }\frac{d(z(n+l), \widetilde z(n+l))}{2^{|n|+2}}+\sum_{|n|> [t_i/2] }\frac{d(z(n+l),\widetilde z(n+l))}{2^{|n|+2}}\bigg)\nonumber\\ &\quad\le \frac{1}{[t_i/2]}\sum_{l=0}^{[t_i/2]-1}\bigg( \frac{\epsilon}{2}+\frac{\text{diam} (G/\Gamma)}{2^{t_i/2}}\bigg) <\epsilon, \end{align} $$
$$ \begin{align} &\!\!\bar{D}_{[t_i/2]}(\pi_{i,q}(z),\pi_{i,q}(\widetilde z))=\frac{1}{[t_i/2]}\sum_{l=0}^{[t_i/2]-1}D(\sigma^lz,\sigma^l\widetilde z)\nonumber\\ &\ \ \overset{(2.21)}= \frac{1}{[t_i/2]}\sum_{l=0}^{[t_i/2]-1}\sum_{n\in\mathbb{Z}}\frac{d(z(n+l),\widetilde z(n+l))}{2^{|n|+2}}\nonumber\\ &\quad\le \frac{1}{[t_i/2]}\sum_{l=0}^{[t_i/2]-1}\bigg(\sum_{|n|\le [t_i/2] }\frac{d(z(n+l), \widetilde z(n+l))}{2^{|n|+2}}+\sum_{|n|> [t_i/2] }\frac{d(z(n+l),\widetilde z(n+l))}{2^{|n|+2}}\bigg)\nonumber\\ &\quad\le \frac{1}{[t_i/2]}\sum_{l=0}^{[t_i/2]-1}\bigg( \frac{\epsilon}{2}+\frac{\text{diam} (G/\Gamma)}{2^{t_i/2}}\bigg) <\epsilon, \end{align} $$
where we use the fact
![]() $t_i\to +\infty $
as
$t_i\to +\infty $
as
![]() $i\to +\infty $
in the last inequality. Notice that the map
$i\to +\infty $
in the last inequality. Notice that the map
![]() $\pi _{i,q}$
is surjective for all
$\pi _{i,q}$
is surjective for all
![]() $i\in \mathbb {N}$
and
$i\in \mathbb {N}$
and
![]() $-t_i\le q\le t_i$
. By equation (2.25), for
$-t_i\le q\le t_i$
. By equation (2.25), for
![]() $i\in \mathbb {N}$
large enough, one has
$i\in \mathbb {N}$
large enough, one has
 $$ \begin{align*}S_{[t_i/2]}(D,\sigma,X_{t_i,q},\epsilon)\le s_{t_i}\bigg(\text{Poly}(G/\Gamma),\frac{\epsilon}{2}\bigg)\quad\text{for all }q\in [-t_i,t_i]\cap\mathbb{Z}.\end{align*} $$
$$ \begin{align*}S_{[t_i/2]}(D,\sigma,X_{t_i,q},\epsilon)\le s_{t_i}\bigg(\text{Poly}(G/\Gamma),\frac{\epsilon}{2}\bigg)\quad\text{for all }q\in [-t_i,t_i]\cap\mathbb{Z}.\end{align*} $$
By the similar arguments, one has part (2). This ends the proof of the Claim.
Hence, by the above Claim and equation (2.23), one has
 $$ \begin{align*} S_{[t_i/2]}(D,\sigma,X_y,\epsilon)&\le (2H_i+1)+ \sum_{q=-t_i}^{t_i}(S_{[t_i/2]}(D,\sigma,X_{t_i,q},\epsilon)+ S_{[t_i/2]}(D,\sigma,X_{t_i,q}^*,\epsilon))\\ \nonumber &\le (2H_i+1)+(2t_i+1)s_{t_i}\bigg(\text{Poly}(G/\Gamma),\frac{\epsilon}{2}\bigg)\end{align*} $$
$$ \begin{align*} S_{[t_i/2]}(D,\sigma,X_y,\epsilon)&\le (2H_i+1)+ \sum_{q=-t_i}^{t_i}(S_{[t_i/2]}(D,\sigma,X_{t_i,q},\epsilon)+ S_{[t_i/2]}(D,\sigma,X_{t_i,q}^*,\epsilon))\\ \nonumber &\le (2H_i+1)+(2t_i+1)s_{t_i}\bigg(\text{Poly}(G/\Gamma),\frac{\epsilon}{2}\bigg)\end{align*} $$
for
![]() $i\in \mathbb {N}$
large enough. Combining this with equation (2.22),
$i\in \mathbb {N}$
large enough. Combining this with equation (2.22),
 $$ \begin{align*} \liminf_{n\to+\infty}\frac{S_{n}(D,\sigma,X_y,\epsilon)}{n^{k+1}} &\le \liminf_{i\to+\infty}\frac{S_{[t_i/2]}(D,\sigma,X_y,\epsilon)}{[t_i/2]^{k+1}}\\ &\le \liminf_{i\to+\infty}\frac{ (2H_i+1)+(2t_i+1)s_{t_i}(\text{Poly}(G/\Gamma),{\epsilon}/{2})}{[t_i/2]^{k+1}}\\ &=0, \end{align*} $$
$$ \begin{align*} \liminf_{n\to+\infty}\frac{S_{n}(D,\sigma,X_y,\epsilon)}{n^{k+1}} &\le \liminf_{i\to+\infty}\frac{S_{[t_i/2]}(D,\sigma,X_y,\epsilon)}{[t_i/2]^{k+1}}\\ &\le \liminf_{i\to+\infty}\frac{ (2H_i+1)+(2t_i+1)s_{t_i}(\text{Poly}(G/\Gamma),{\epsilon}/{2})}{[t_i/2]^{k+1}}\\ &=0, \end{align*} $$
where we used the assumption
![]() $t_i=[H_i/2]$
. This implies that
$t_i=[H_i/2]$
. This implies that
![]() $(X_y,\sigma )$
has polynomial mean complexity, since the above inequality is true for all
$(X_y,\sigma )$
has polynomial mean complexity, since the above inequality is true for all
![]() $\epsilon>0$
. This ends the proof of Step 2.
$\epsilon>0$
. This ends the proof of Step 2.
Remark 2.7. In the proof above, we use dynamics on infinite products. Precisely, we show that if the logarithmic Sarnak’s conjecture does not hold, one can find a point in an infinite product space
![]() $(G/\Gamma \cup \{p\})^{\mathbb {Z}}$
for which the logarithmic averages are almost equal to the short uniform averages of the corresponding space
$(G/\Gamma \cup \{p\})^{\mathbb {Z}}$
for which the logarithmic averages are almost equal to the short uniform averages of the corresponding space
![]() $G/\Gamma $
. We remark that the idea behind the construction is similar to that in [Reference El Abdalaoui, Kułaga-Przymus, Lemańczyk and de la Rue4] where the authors also use dynamics on infinite products. They show that what they call the strong MOMO property is equivalent to Sarnak’s conjecture (see Corollary 9).
$G/\Gamma $
. We remark that the idea behind the construction is similar to that in [Reference El Abdalaoui, Kułaga-Przymus, Lemańczyk and de la Rue4] where the authors also use dynamics on infinite products. They show that what they call the strong MOMO property is equivalent to Sarnak’s conjecture (see Corollary 9).
2.2 Proof of statement (3) implies statement (2) in Theorem 1.1
To get the proof, we first discuss a t.d.s. with the so-called small boundary property, then we obtain a key proposition for the proof, and finally we give the proof. We start with the notion of small boundary property.
For a t.d.s.
![]() $(X,T)$
, a subset E of X is called T-small (or simply small when there is no diffusion) if
$(X,T)$
, a subset E of X is called T-small (or simply small when there is no diffusion) if
 $$ \begin{align*}\lim_{N\to+\infty}\frac{1}{N}\sum_{n=0}^{N-1}\mathbf{1}_{E}(T^nx)=0\end{align*} $$
$$ \begin{align*}\lim_{N\to+\infty}\frac{1}{N}\sum_{n=0}^{N-1}\mathbf{1}_{E}(T^nx)=0\end{align*} $$
uniformly for
![]() $x\in X$
. It is not hard to show that a closed subset E of X is small if and only if
$x\in X$
. It is not hard to show that a closed subset E of X is small if and only if
![]() $\nu (E)=0$
for all
$\nu (E)=0$
for all
![]() $\nu \in \mathcal {M}(X,T)$
. For a subset U of X, we say U has a small boundary if
$\nu \in \mathcal {M}(X,T)$
. For a subset U of X, we say U has a small boundary if
![]() $\partial U$
is small. We say
$\partial U$
is small. We say
![]() $(X,T)$
has a small boundary property if for any
$(X,T)$
has a small boundary property if for any
![]() $x\in X$
and any open neighborhood V of x, there exists an open neighborhood W of x such that
$x\in X$
and any open neighborhood V of x, there exists an open neighborhood W of x such that
![]() $W\subset V$
and W has a small boundary. The following lemma indicates that when X has the small boundary property, then the logarithmic Sarnak conjecture can be verified through easier conditions.
$W\subset V$
and W has a small boundary. The following lemma indicates that when X has the small boundary property, then the logarithmic Sarnak conjecture can be verified through easier conditions.
Lemma 2.8. Let
![]() $(X,T)$
be a t.d.s. with small the boundary property. Then the logarithmic Sarnak conjecture holds for
$(X,T)$
be a t.d.s. with small the boundary property. Then the logarithmic Sarnak conjecture holds for
![]() $(X,T)$
if and only if for any subset U of X with a small boundary, one has
$(X,T)$
if and only if for any subset U of X with a small boundary, one has
for all
![]() $x\in X$
.
$x\in X$
.
Proof. First, we assume that equation (2.26) holds for any subset U of X with small boundary and
![]() $x\in X$
. For a given
$x\in X$
. For a given
![]() $f\in C(X)$
and fixed
$f\in C(X)$
and fixed
![]() $\delta>0$
, let
$\delta>0$
, let
Let
![]() $\mathcal {P}=\{P_1,P_2,\ldots ,P_k\}$
be a partition of X with diameter smaller than
$\mathcal {P}=\{P_1,P_2,\ldots ,P_k\}$
be a partition of X with diameter smaller than
![]() $\delta $
and each element of
$\delta $
and each element of
![]() $\mathcal {P}$
has a small boundary. For
$\mathcal {P}$
has a small boundary. For
![]() $1\le i\le k$
, we fix points
$1\le i\le k$
, we fix points
![]() $x_i\in P_i$
and define
$x_i\in P_i$
and define
![]() $\bar f(x)=f(x_i)$
if
$\bar f(x)=f(x_i)$
if
![]() $x\in P_i$
. Then,
$x\in P_i$
. Then,
![]() $\bar f(x)=\sum _{i=1}^k f(x_i)\mathbf {1}_{P_i}(x)$
and by equation (2.26),
$\bar f(x)=\sum _{i=1}^k f(x_i)\mathbf {1}_{P_i}(x)$
and by equation (2.26),
for all
![]() $x\in X$
. Since
$x\in X$
. Since
![]() $\|\bar f-f\|_{\infty }\le \epsilon $
, we have
$\|\bar f-f\|_{\infty }\le \epsilon $
, we have
 $$ \begin{align*} &\limsup_{N\to+\infty}|\mathbb{E}_{n\le N}^{\log} f(T^nx)\mu(n)|\\ &\quad\le \limsup_{N\to+\infty}|\mathbb{E}_{n\le N}^{\log}\bar f(T^nx)\mu(n)|+\limsup_{N\to+\infty}\mathbb{E}_{n\le N}^{\log} \|\bar f-f\|_{\infty}\cdot|\mu(n)|\\ &\quad\le \epsilon \end{align*} $$
$$ \begin{align*} &\limsup_{N\to+\infty}|\mathbb{E}_{n\le N}^{\log} f(T^nx)\mu(n)|\\ &\quad\le \limsup_{N\to+\infty}|\mathbb{E}_{n\le N}^{\log}\bar f(T^nx)\mu(n)|+\limsup_{N\to+\infty}\mathbb{E}_{n\le N}^{\log} \|\bar f-f\|_{\infty}\cdot|\mu(n)|\\ &\quad\le \epsilon \end{align*} $$
for all
![]() $x\in X$
. By taking
$x\in X$
. By taking
![]() $\delta \to 0$
and then
$\delta \to 0$
and then
![]() $\epsilon \to 0$
, one has
$\epsilon \to 0$
, one has
for all
![]() $x\in X$
. This implies the logarithmic Sarnak conjecture holds for
$x\in X$
. This implies the logarithmic Sarnak conjecture holds for
![]() $(X,T)$
since f is arbitrary.
$(X,T)$
since f is arbitrary.
Conversely, we assume that the logarithmic Sarnak conjecture holds for
![]() $(X,T)$
. Let U be a subset of X with small boundary. Fix
$(X,T)$
. Let U be a subset of X with small boundary. Fix
![]() $\delta>0$
. By a result of Shub and Weiss (see [Reference Shub and Weiss20, p. 537]), we can find
$\delta>0$
. By a result of Shub and Weiss (see [Reference Shub and Weiss20, p. 537]), we can find
![]() $\epsilon>0$
such that for N large enough,
$\epsilon>0$
such that for N large enough,
 $$ \begin{align*} \frac{1}{N}\sum_{n=1}^{N}\mathbf{1}_{B(\partial U,\epsilon)}(T^nx)\le \frac{\delta}{2} \end{align*} $$
$$ \begin{align*} \frac{1}{N}\sum_{n=1}^{N}\mathbf{1}_{B(\partial U,\epsilon)}(T^nx)\le \frac{\delta}{2} \end{align*} $$
for all
![]() $x\in X$
, where
$x\in X$
, where
![]() $B(\partial U,\epsilon )=\{y\in X: d(y,\partial U)<\epsilon \}$
. Moreover, for N large enough,
$B(\partial U,\epsilon )=\{y\in X: d(y,\partial U)<\epsilon \}$
. Moreover, for N large enough,
 $$ \begin{align} \begin{split} \mathbb{E}_{n\le N}^{\log}\mathbf{1}_{B(\partial U,\epsilon)}(T^nx)&= \frac{1}{M_N}\sum_{n=1}^{N}\frac{\mathbf{1}_{B(\partial U,\epsilon)}(T^nx)}{n}\\ &=\frac{1}{M_N}\bigg(\frac{S_N(x)}{N}+\sum_{j=1}^{N-1}\frac{S_j(x)}{j} \frac{1}{j+1}\bigg)\\ &\le \delta \end{split} \end{align} $$
$$ \begin{align} \begin{split} \mathbb{E}_{n\le N}^{\log}\mathbf{1}_{B(\partial U,\epsilon)}(T^nx)&= \frac{1}{M_N}\sum_{n=1}^{N}\frac{\mathbf{1}_{B(\partial U,\epsilon)}(T^nx)}{n}\\ &=\frac{1}{M_N}\bigg(\frac{S_N(x)}{N}+\sum_{j=1}^{N-1}\frac{S_j(x)}{j} \frac{1}{j+1}\bigg)\\ &\le \delta \end{split} \end{align} $$
for all
![]() $x\in X$
, where we simply write
$x\in X$
, where we simply write
![]() $M_N=\kern-1pt\sum _{n=1}^N({1}/{n})$
and
$M_N=\kern-1pt\sum _{n=1}^N({1}/{n})$
and
![]() $S_j(x)=\kern-1pt\sum _{n=1}^j \kern-1pt\mathbf {1}_{B(\partial U,\epsilon )}(T^nx)$
for
$S_j(x)=\kern-1pt\sum _{n=1}^j \kern-1pt\mathbf {1}_{B(\partial U,\epsilon )}(T^nx)$
for
![]() $j\in \mathbb {N}$
.
$j\in \mathbb {N}$
.
Using Urysohn’s lemma, there exists a continuous function
![]() $h{\kern-1.2pt}:{\kern-1.2pt}X{\kern-1.3pt}\to{\kern-1.2pt} \mathbb {R}$
with
$h{\kern-1.2pt}:{\kern-1.2pt}X{\kern-1.3pt}\to{\kern-1.2pt} \mathbb {R}$
with
![]() $0{\kern-1.2pt}\le{\kern-1.2pt} h{\kern-1.2pt}\le{\kern-1.2pt} 1$
such that
$0{\kern-1.2pt}\le{\kern-1.2pt} h{\kern-1.2pt}\le{\kern-1.2pt} 1$
such that
![]() $h(x)=1$
for
$h(x)=1$
for
![]() $x\in U\setminus B(\partial U,\epsilon )$
and
$x\in U\setminus B(\partial U,\epsilon )$
and
![]() $h(x)=0$
for
$h(x)=0$
for
![]() $x\in X\setminus \big (U\cup B(\partial U,\epsilon )\big )$
. Since the logarithmic Sarnak conjecture holds for
$x\in X\setminus \big (U\cup B(\partial U,\epsilon )\big )$
. Since the logarithmic Sarnak conjecture holds for
![]() $(X,T)$
, one has
$(X,T)$
, one has
for all
![]() $x\in X$
. Combining this equality with equation (2.27), we obtain
$x\in X$
. Combining this equality with equation (2.27), we obtain
 $$ \begin{align*} &\limsup_{N\to+\infty}|\mathbb{E}_{n\le N}^{\log} 1_U(T^nx)\mu (n)|\\ &\quad\le \limsup_{N\to+\infty}|\mathbb{E}_{n\le N}^{\log} h(T^nx)\mu (n)| +\limsup_{N\to+\infty}\mathbb{E}_{n\le N}^{\log} |h(T^nx)-1_U(T^nx)|\\ &\quad\le \limsup_{N\to+\infty}\mathbb{E}_{n\le N}^{\log} 1_{B(\partial U,\epsilon)}(T^nx)\le \delta \end{align*} $$
$$ \begin{align*} &\limsup_{N\to+\infty}|\mathbb{E}_{n\le N}^{\log} 1_U(T^nx)\mu (n)|\\ &\quad\le \limsup_{N\to+\infty}|\mathbb{E}_{n\le N}^{\log} h(T^nx)\mu (n)| +\limsup_{N\to+\infty}\mathbb{E}_{n\le N}^{\log} |h(T^nx)-1_U(T^nx)|\\ &\quad\le \limsup_{N\to+\infty}\mathbb{E}_{n\le N}^{\log} 1_{B(\partial U,\epsilon)}(T^nx)\le \delta \end{align*} $$
for all
![]() $x\in X$
. By taking
$x\in X$
. By taking
![]() $\delta \to 0$
, we have
$\delta \to 0$
, we have
for all
![]() $x\in X$
. This ends the proof of Lemma 2.8.
$x\in X$
. This ends the proof of Lemma 2.8.
The next lemma concerns the coding of a subset with small boundary.
Lemma 2.9. Let
![]() $(X,T)$
be a t.d.s. and U be a subset of X with small boundary. For
$(X,T)$
be a t.d.s. and U be a subset of X with small boundary. For
![]() $x\in X$
, we associate an
$x\in X$
, we associate an
![]() $\hat x\in \{0,1\}^{\mathbb {Z}}$
such that
$\hat x\in \{0,1\}^{\mathbb {Z}}$
such that
![]() $\hat x(n)=1$
if
$\hat x(n)=1$
if
![]() $T^nx\in U$
and
$T^nx\in U$
and
![]() $\hat x(n)=0$
otherwise. Then for
$\hat x(n)=0$
otherwise. Then for
![]() $\delta>0$
, there exist
$\delta>0$
, there exist
![]() $\epsilon>0$
and
$\epsilon>0$
and
![]() $N_\delta \in \mathbb {N}$
such that for all
$N_\delta \in \mathbb {N}$
such that for all
![]() $N\ge N_\delta $
and any
$N\ge N_\delta $
and any
![]() $x_1,x_2\in X$
with
$x_1,x_2\in X$
with
![]() $\bar d_N(x_1,x_2)< \epsilon $
, one has
$\bar d_N(x_1,x_2)< \epsilon $
, one has
Proof. We fix an
![]() $\delta \in (0,+\infty )$
and a non-empty subset U of X with small boundary. By a result of Shub and Weiss (see [Reference Shub and Weiss20, p. 537]), there exist
$\delta \in (0,+\infty )$
and a non-empty subset U of X with small boundary. By a result of Shub and Weiss (see [Reference Shub and Weiss20, p. 537]), there exist
![]() $N_\delta \in \mathbb {N}$
and
$N_\delta \in \mathbb {N}$
and
![]() $\epsilon _0\in (0,+\infty )$
such that
$\epsilon _0\in (0,+\infty )$
such that
 $$ \begin{align}\sup_{x\in X,N\ge N_\delta}\frac{1}{N}\sum_{n=0}^{N-1}\mathbf{1}_{B(\partial U,\epsilon_0)}(T^nx)<\delta, \end{align} $$
$$ \begin{align}\sup_{x\in X,N\ge N_\delta}\frac{1}{N}\sum_{n=0}^{N-1}\mathbf{1}_{B(\partial U,\epsilon_0)}(T^nx)<\delta, \end{align} $$
where
![]() $B(\partial U,\epsilon _0)=\{z\in X:d(z,z')<\epsilon _0\text { for all }z'\in \partial U \}$
if
$B(\partial U,\epsilon _0)=\{z\in X:d(z,z')<\epsilon _0\text { for all }z'\in \partial U \}$
if
![]() $\partial U $
is not empty and
$\partial U $
is not empty and
![]() $B(\partial U,\epsilon _0)=\emptyset $
if
$B(\partial U,\epsilon _0)=\emptyset $
if
![]() $\partial U $
is empty.
$\partial U $
is empty.
We notice that
![]() $\overline {U\setminus B(\partial U,\epsilon _0)}\cap \overline {X\setminus U}=\emptyset $
and
$\overline {U\setminus B(\partial U,\epsilon _0)}\cap \overline {X\setminus U}=\emptyset $
and
![]() $\overline {(X\setminus U)\setminus B(\partial U,\epsilon _0)}\cap \overline {U}=\emptyset $
. Thus, we can find
$\overline {(X\setminus U)\setminus B(\partial U,\epsilon _0)}\cap \overline {U}=\emptyset $
. Thus, we can find
![]() $\epsilon \in (0,\delta ^2)$
such that when
$\epsilon \in (0,\delta ^2)$
such that when
![]() $x,y\in X$
with
$x,y\in X$
with
![]() $d(x,y)<\sqrt {\epsilon }$
, if
$d(x,y)<\sqrt {\epsilon }$
, if
![]() $x\in U\setminus B(\partial U,\epsilon _0)$
(respectively
$x\in U\setminus B(\partial U,\epsilon _0)$
(respectively
![]() $x\in (X\setminus U)\setminus B(\partial U,\epsilon _0)$
), then
$x\in (X\setminus U)\setminus B(\partial U,\epsilon _0)$
), then
![]() $y\in U$
(respectively
$y\in U$
(respectively
![]() $y\in X\setminus U$
). We are to show that
$y\in X\setminus U$
). We are to show that
![]() $\epsilon $
is the constant as required. We fix
$\epsilon $
is the constant as required. We fix
![]() $N\ge N_\delta $
and
$N\ge N_\delta $
and
![]() $x_1,x_2\in X$
with
$x_1,x_2\in X$
with
![]() $\bar d_N(x_1,x_2)< \epsilon $
. Set
$\bar d_N(x_1,x_2)< \epsilon $
. Set
By equation (2.28),
![]() $\sharp C\le \delta N$
. Put
$\sharp C\le \delta N$
. Put
One has
![]() $\sharp \mathcal {A}\ge (1-\sqrt {\epsilon })N$
and
$\sharp \mathcal {A}\ge (1-\sqrt {\epsilon })N$
and
![]() $\hat {x_1}(n)=\hat {x_2}(n) \text { for all }n\in \mathcal {A}\setminus C$
. Therefore,
$\hat {x_1}(n)=\hat {x_2}(n) \text { for all }n\in \mathcal {A}\setminus C$
. Therefore,
Since
![]() $\delta>\sqrt {\epsilon }$
, one has
$\delta>\sqrt {\epsilon }$
, one has
This ends the proof of Lemma 2.9.
Recall that the metric on
![]() $\{0,1\}^{\mathbb {Z}}$
is defined by
$\{0,1\}^{\mathbb {Z}}$
is defined by
 $$ \begin{align}d(x,y)=\sum_{n\in\mathbb{Z}}\frac{|x(n)-y(n)|}{2^{|n|+2}}\end{align} $$
$$ \begin{align}d(x,y)=\sum_{n\in\mathbb{Z}}\frac{|x(n)-y(n)|}{2^{|n|+2}}\end{align} $$
for
![]() $x=(x(n))_{n\in \mathbb {Z}}, y=(y(n))_{n\in \mathbb {Z}}\in \{0,1\}^{\mathbb {Z}}$
. We have the following lemma which is key for the proof of statement (3) implies statement (2) in Theorem 1.1.
$x=(x(n))_{n\in \mathbb {Z}}, y=(y(n))_{n\in \mathbb {Z}}\in \{0,1\}^{\mathbb {Z}}$
. We have the following lemma which is key for the proof of statement (3) implies statement (2) in Theorem 1.1.
Now we show a key proposition for the proof of statement (3) implies statement (2) in Theorem 1.1.
Proposition 2.10. Let
![]() $(X,T)$
be a t.d.s. and U be a subset of X with small boundary. For
$(X,T)$
be a t.d.s. and U be a subset of X with small boundary. For
![]() $x\in X$
, we associate an
$x\in X$
, we associate an
![]() $\hat x\in \{0,1\}^{\mathbb {Z}}$
such that
$\hat x\in \{0,1\}^{\mathbb {Z}}$
such that
![]() $\hat x(n)=1$
if
$\hat x(n)=1$
if
![]() $T^nx\in U$
and
$T^nx\in U$
and
![]() $0$
if
$0$
if
![]() $T^nx\in X\setminus U$
. Then for each
$T^nx\in X\setminus U$
. Then for each
![]() $\delta>0$
, we can find
$\delta>0$
, we can find
![]() $\epsilon :=\epsilon (\delta )>0$
such that
$\epsilon :=\epsilon (\delta )>0$
such that
![]() $S_N(d,\sigma ,\hat {X},\delta )\le S_N(d, T,X,\epsilon )$
for
$S_N(d,\sigma ,\hat {X},\delta )\le S_N(d, T,X,\epsilon )$
for
![]() $N\in \mathbb {N}$
large enough, where
$N\in \mathbb {N}$
large enough, where
![]() $\hat {X}=\overline {\{\hat x:x\in X\}}$
and
$\hat {X}=\overline {\{\hat x:x\in X\}}$
and
![]() $\sigma :\{0,1\}^{\mathbb {Z}}\rightarrow \{0,1\}^{\mathbb {Z}}$
is the left shift.
$\sigma :\{0,1\}^{\mathbb {Z}}\rightarrow \{0,1\}^{\mathbb {Z}}$
is the left shift.
Proof. We fix a
![]() $\delta>0$
and a non-empty subset U of X with small boundary. We are to find
$\delta>0$
and a non-empty subset U of X with small boundary. We are to find
![]() $\epsilon \in (0,+\infty )$
such that
$\epsilon \in (0,+\infty )$
such that
![]() $S_N(d,\sigma ,\hat {X},\delta )\le S_N(d, T,X,\epsilon )$
for N large enough. To do this, we choose
$S_N(d,\sigma ,\hat {X},\delta )\le S_N(d, T,X,\epsilon )$
for N large enough. To do this, we choose
![]() $L\in \mathbb {N}$
and
$L\in \mathbb {N}$
and
![]() $\delta '>0$
such that
$\delta '>0$
such that
By Lemma 2.9, there exists
![]() $\epsilon :=\epsilon (\delta ')>0$
such that for
$\epsilon :=\epsilon (\delta ')>0$
such that for
![]() $N\in \mathbb {N}$
large enough and
$N\in \mathbb {N}$
large enough and
![]() $x_1,x_2\in X$
with
$x_1,x_2\in X$
with
![]() $\bar d_N(x_1,x_2)< \epsilon $
, one has
$\bar d_N(x_1,x_2)< \epsilon $
, one has
Fix
![]() $x_1,x_2\in X$
with
$x_1,x_2\in X$
with
![]() $\bar d_N(x_1,x_2)< \epsilon $
and put
$\bar d_N(x_1,x_2)< \epsilon $
and put
By equation (2.31), we have for
![]() $N\in \mathbb {N}$
large enough,
$N\in \mathbb {N}$
large enough,
Notice that
![]() $d(\sigma ^n\hat {x_1},\sigma ^n\hat {x_2})\le 1$
for
$d(\sigma ^n\hat {x_1},\sigma ^n\hat {x_2})\le 1$
for
![]() $n\in \mathcal {C}_N$
. One has
$n\in \mathcal {C}_N$
. One has
 $$ \begin{align*} \bar d_N(\hat{x_1},\hat{x_2})&=\frac{1}{N}\bigg(\sum_{n\in \mathcal{C}_N}d(\sigma^n\hat{x_1},\sigma^n\hat{x_2})+\sum_{n\in[0,N-1]\setminus\mathcal{C}_N}d(\sigma^n\hat{x_1},\sigma^n\hat{x_2})\bigg) \\ &\overset{(2.29)}\le \frac{1}{N}\bigg(\sum_{n\in \mathcal{C}_N}1+\sum_{n\in[0,N-1]\setminus\mathcal{C}_N}\frac{2}{2^L}\bigg) \\ &=\frac{1}{N}\bigg(\sharp\mathcal{C}_N+\frac{2}{2^L}(N-\sharp\mathcal{C}_N)\bigg) \\ &\overset{(2.30)} \le4\delta'L+\frac{2}{2^L}<\delta. \end{align*} $$
$$ \begin{align*} \bar d_N(\hat{x_1},\hat{x_2})&=\frac{1}{N}\bigg(\sum_{n\in \mathcal{C}_N}d(\sigma^n\hat{x_1},\sigma^n\hat{x_2})+\sum_{n\in[0,N-1]\setminus\mathcal{C}_N}d(\sigma^n\hat{x_1},\sigma^n\hat{x_2})\bigg) \\ &\overset{(2.29)}\le \frac{1}{N}\bigg(\sum_{n\in \mathcal{C}_N}1+\sum_{n\in[0,N-1]\setminus\mathcal{C}_N}\frac{2}{2^L}\bigg) \\ &=\frac{1}{N}\bigg(\sharp\mathcal{C}_N+\frac{2}{2^L}(N-\sharp\mathcal{C}_N)\bigg) \\ &\overset{(2.30)} \le4\delta'L+\frac{2}{2^L}<\delta. \end{align*} $$
Therefore,
![]() $S_N(d,\sigma ,\hat {X},\delta )\le S_N(d, T,X,\epsilon )$
for
$S_N(d,\sigma ,\hat {X},\delta )\le S_N(d, T,X,\epsilon )$
for
![]() $N\in \mathbb {N}$
large enough and
$N\in \mathbb {N}$
large enough and
![]() $\epsilon $
is the constant as required. This ends the proof of Proposition 2.10.
$\epsilon $
is the constant as required. This ends the proof of Proposition 2.10.
For a t.d.s.
![]() $(X,T)$
, Lindenstrauss and Weiss [Reference Lindenstrauss and Weiss15] introduced the notion of mean dimension, denoted by
$(X,T)$
, Lindenstrauss and Weiss [Reference Lindenstrauss and Weiss15] introduced the notion of mean dimension, denoted by
![]() $\mathrm {mdim}(X,T)$
. It is well known that for a t.d.s.
$\mathrm {mdim}(X,T)$
. It is well known that for a t.d.s.
![]() $(X,T)$
, if
$(X,T)$
, if
![]() $h_{\mathrm{top}}(T )<\infty $
or the topological dimension of X is finite, then
$h_{\mathrm{top}}(T )<\infty $
or the topological dimension of X is finite, then
![]() $\mathrm {mdim}(X,T ) = 0$
(see [Reference Lindenstrauss and Weiss15, Definition 2.6 and Theorem 4.2]).
$\mathrm {mdim}(X,T ) = 0$
(see [Reference Lindenstrauss and Weiss15, Definition 2.6 and Theorem 4.2]).
Now we are ready to finish the proof of Theorem 1.1.
Proof of Theorem 1.1: (3)
 $\Longrightarrow $
(2)
$\Longrightarrow $
(2)
Assume that Theorem 1.1(3) holds. Now we are going to show that Theorem 1.1(2) holds. Assume the contrary that Theorem 1.1(2) does not hold, then there exists a t.d.s.
![]() $(X,T)$
with polynomial mean complexity such that the logarithmic Sarnak conjecture does not hold for
$(X,T)$
with polynomial mean complexity such that the logarithmic Sarnak conjecture does not hold for
![]() $(X,T)$
.
$(X,T)$
.
Let
![]() $(Y,S)$
be an irrational rotation on the circle. Then
$(Y,S)$
be an irrational rotation on the circle. Then
![]() $(X\times Y,T\times S)$
has polynomial mean complexity as well as zero mean dimension and admits a non-periodic minimal factor
$(X\times Y,T\times S)$
has polynomial mean complexity as well as zero mean dimension and admits a non-periodic minimal factor
![]() $(Y,S)$
. Hence,
$(Y,S)$
. Hence,
![]() $(X \times Y,T\times S)$
has small boundary property by [Reference Lindenstrauss14, Theorem 6.2]. Since the logarithmic Sarnak conjecture does not hold for
$(X \times Y,T\times S)$
has small boundary property by [Reference Lindenstrauss14, Theorem 6.2]. Since the logarithmic Sarnak conjecture does not hold for
![]() $(X,T)$
, neither does
$(X,T)$
, neither does
![]() $(X \times Y,T\times S)$
. By Lemma 2.8, there is a subset U of
$(X \times Y,T\times S)$
. By Lemma 2.8, there is a subset U of
![]() $X\times Y$
with small boundary and
$X\times Y$
with small boundary and
![]() $w\in X\times Y$
such that
$w\in X\times Y$
such that
Combining this with Proposition 2.10, the
![]() $\{0,1\}$
-symbolic system
$\{0,1\}$
-symbolic system
![]() $(\overline {\{\hat z:z\in X\times Y\}},\sigma )$
has polynomial mean complexity and
$(\overline {\{\hat z:z\in X\times Y\}},\sigma )$
has polynomial mean complexity and
where
![]() $F_0(\hat z)=\hat z(0)$
for
$F_0(\hat z)=\hat z(0)$
for
![]() $z\in X\times Y$
, which contradicts the assumption that Theorem 1.1(3) holds. This ends the proof of (3)
$z\in X\times Y$
, which contradicts the assumption that Theorem 1.1(3) holds. This ends the proof of (3)
![]() $\Longrightarrow $
(2) in Theorem 1.1, and hence the proof of Theorem 1.1.
$\Longrightarrow $
(2) in Theorem 1.1, and hence the proof of Theorem 1.1.
3 Proof of Theorem 1.3
In this section, we will prove Theorem 1.3. First, we recall the definition of packing dimension. Let X be a metric space endowed with a metric d and E be a subset of X. We say that a collection of balls
![]() $\{U_n\}_{n\in \mathbb {N}}\subset X$
is a
$\{U_n\}_{n\in \mathbb {N}}\subset X$
is a
![]() $\delta $
-packing of E if the diameter of the balls is not larger than
$\delta $
-packing of E if the diameter of the balls is not larger than
![]() $\delta $
, they are pairwise disjoint, and their centers belong to E. For
$\delta $
, they are pairwise disjoint, and their centers belong to E. For
![]() $\alpha \in \mathbb {R}$
, the
$\alpha \in \mathbb {R}$
, the
![]() $\alpha $
-dimensional pre-packing measure of E is given by
$\alpha $
-dimensional pre-packing measure of E is given by
 $$ \begin{align*}P(E,\alpha)=\lim_{\delta\to0}\sup\bigg\{\sum_{n\in\mathbb{N}} \text{diam}(U_n)^\alpha\bigg\},\end{align*} $$
$$ \begin{align*}P(E,\alpha)=\lim_{\delta\to0}\sup\bigg\{\sum_{n\in\mathbb{N}} \text{diam}(U_n)^\alpha\bigg\},\end{align*} $$
where the supremum is taken over all
![]() $\delta $
-packings of E. The
$\delta $
-packings of E. The
![]() $\alpha $
-dimensional packing measure of E is defined by
$\alpha $
-dimensional packing measure of E is defined by
 $$ \begin{align*}p(E, \alpha) = \inf\bigg\{\sum_{i\in\mathbb{N}} P(E_i , \alpha)\bigg\},\end{align*} $$
$$ \begin{align*}p(E, \alpha) = \inf\bigg\{\sum_{i\in\mathbb{N}} P(E_i , \alpha)\bigg\},\end{align*} $$
where the infimum is taken over all covers
![]() $\{E_i\}_{i\in \mathbb {N}}$
of E. Finally, we define the packing dimension of E by
$\{E_i\}_{i\in \mathbb {N}}$
of E. Finally, we define the packing dimension of E by
For
![]() $x\in [0,1]$
and
$x\in [0,1]$
and
![]() $r>0$
, let
$r>0$
, let
![]() $B(x,r)=\{y\in [0,1],|x-y|<r\}$
. To prove Theorem 1.3, we need several lemmas. We begin with the following lemma (see [Reference Fan, Lau and Rao5]).
$B(x,r)=\{y\in [0,1],|x-y|<r\}$
. To prove Theorem 1.3, we need several lemmas. We begin with the following lemma (see [Reference Fan, Lau and Rao5]).
Lemma 3.1. Let
![]() $\mu $
be a Borel probability measure on
$\mu $
be a Borel probability measure on
![]() $[0,1]$
. Then,
$[0,1]$
. Then,
where
![]() $\mathrm{Dim}^*\mu =\mathrm{ess}\sup \limsup _{r\to 0}({\log \mu (B(x,r))}/{\log r})$
.
$\mathrm{Dim}^*\mu =\mathrm{ess}\sup \limsup _{r\to 0}({\log \mu (B(x,r))}/{\log r})$
.
We also need the following lemma [Reference Mattila17, Theorem 2.1].
Lemma 3.2. Let
![]() ${\mathcal B}=\{B(x_i,r_i)\}_{i\in \mathcal I}$
be a family of open balls in
${\mathcal B}=\{B(x_i,r_i)\}_{i\in \mathcal I}$
be a family of open balls in
![]() $[0,1]$
. Then there exists a finite or countable subfamily
$[0,1]$
. Then there exists a finite or countable subfamily
![]() ${\mathcal B'}=\{B(x_i,r_i)\}_{i\in {\mathcal I}'}$
of pairwise disjoint balls in
${\mathcal B'}=\{B(x_i,r_i)\}_{i\in {\mathcal I}'}$
of pairwise disjoint balls in
![]() ${\mathcal B}$
such that
${\mathcal B}$
such that
Let
![]() $\mathbb {T}$
be the unit circle on the complex plane
$\mathbb {T}$
be the unit circle on the complex plane
![]() $\mathbb {C}$
. Recall that
$\mathbb {C}$
. Recall that
![]() $e(t)=e^{2\pi t}$
for any
$e(t)=e^{2\pi t}$
for any
![]() $t\in \mathbb {R}$
. We will prove the following lemma by using Lemmas 3.1 and 3.2. Define a metric d on
$t\in \mathbb {R}$
. We will prove the following lemma by using Lemmas 3.1 and 3.2. Define a metric d on
![]() $[0,1]\times \mathbb {T}$
such that
$[0,1]\times \mathbb {T}$
such that
![]() $d((x_1,z_1),(x_2,z_2))=\max \{ |x_1-x_2|,|z_1-z_2|\}$
for
$d((x_1,z_1),(x_2,z_2))=\max \{ |x_1-x_2|,|z_1-z_2|\}$
for
![]() $(x_1,z_1),(x_2,z_2)\in [0,1]\times \mathbb {T}$
.
$(x_1,z_1),(x_2,z_2)\in [0,1]\times \mathbb {T}$
.
Lemma 3.3. Let C be a compact subset of
![]() $[0,1]$
with
$[0,1]$
with
![]() $\mathrm{Dim}_P C<\tau $
for some given
$\mathrm{Dim}_P C<\tau $
for some given
![]() $\tau>0$
. Then the t.d.s.
$\tau>0$
. Then the t.d.s.
![]() $T: C\times \mathbb {T}\to C\times \mathbb {T}$
defined by
$T: C\times \mathbb {T}\to C\times \mathbb {T}$
defined by
![]() $T\big (x,e(y)\big )= \big (x,e(y+x)\big )$
satisfies for any
$T\big (x,e(y)\big )= \big (x,e(y+x)\big )$
satisfies for any
![]() $\rho \in \mathcal {M}(C\times \mathbb {T},T)$
and any
$\rho \in \mathcal {M}(C\times \mathbb {T},T)$
and any
![]() $\epsilon>0$
,
$\epsilon>0$
,
Proof. Fix a constant
![]() $\tau _0$
with
$\tau _0$
with
![]() $\mathrm{Dim}_P C<\tau _0<\tau $
. For a given
$\mathrm{Dim}_P C<\tau _0<\tau $
. For a given
![]() $\rho \in \mathcal {M}(C\times \mathbb {T},T)$
, let m be the projection of
$\rho \in \mathcal {M}(C\times \mathbb {T},T)$
, let m be the projection of
![]() $\rho $
onto the first coordinate. Fix
$\rho $
onto the first coordinate. Fix
![]() $\epsilon \in (0,1)$
. To prove Lemma 3.3, it suffices to demonstrate
$\epsilon \in (0,1)$
. To prove Lemma 3.3, it suffices to demonstrate
First we note that
![]() $m(C)=1$
. Using Lemma 3.1, one has
$m(C)=1$
. Using Lemma 3.1, one has
![]() $\mathrm{Dim}^*m<\tau _0$
and there exist a subset
$\mathrm{Dim}^*m<\tau _0$
and there exist a subset
![]() $\widetilde C$
of C and a constant
$\widetilde C$
of C and a constant
![]() $r_\epsilon \in (0,1)$
such that:
$r_\epsilon \in (0,1)$
such that:
-
(1)
 $\widetilde C$
is compact and
$\widetilde C$
is compact and
 $m(\widetilde C)>1-\epsilon $
;
$m(\widetilde C)>1-\epsilon $
; -
(2)
 $m(B(x,r))> r^{\tau _0}$
for
$m(B(x,r))> r^{\tau _0}$
for
 $0<r\le r_\epsilon $
and
$0<r\le r_\epsilon $
and
 $x\in \widetilde C$
.
$x\in \widetilde C$
.
For any given integer
![]() $n>{\epsilon }/{10r_\epsilon }$
, set
$n>{\epsilon }/{10r_\epsilon }$
, set
![]() $\mathcal {B}_n=\{B(x,{\epsilon }/{10n})\}_{x\in \widetilde C}$
. By Lemma 3.2, there exist pairwise disjoint balls
$\mathcal {B}_n=\{B(x,{\epsilon }/{10n})\}_{x\in \widetilde C}$
. By Lemma 3.2, there exist pairwise disjoint balls
![]() $\mathcal {B}^{\prime }_n=\{B(x_i,{\epsilon }/{10n})\}_{i\in \mathcal {I}_n}$
in
$\mathcal {B}^{\prime }_n=\{B(x_i,{\epsilon }/{10n})\}_{i\in \mathcal {I}_n}$
in
![]() $\mathcal {B}$
such that
$\mathcal {B}$
such that
 $$ \begin{align*}\widetilde C\subset \bigcup_{i\in\mathcal{I}^{\prime}_n}B\bigg(x_i,\frac{\epsilon}{2n}\bigg).\end{align*} $$
$$ \begin{align*}\widetilde C\subset \bigcup_{i\in\mathcal{I}^{\prime}_n}B\bigg(x_i,\frac{\epsilon}{2n}\bigg).\end{align*} $$
Since
![]() ${\epsilon }/{10n}<r_\epsilon $
, one deduces that
${\epsilon }/{10n}<r_\epsilon $
, one deduces that
 $$ \begin{align*}m\bigg(B\bigg(x,\frac{\epsilon}{10n}\bigg)\bigg)>\bigg(\frac{\epsilon}{10n}\bigg)^{\tau_0}\quad\text{for all }x\in \widetilde C.\end{align*} $$
$$ \begin{align*}m\bigg(B\bigg(x,\frac{\epsilon}{10n}\bigg)\bigg)>\bigg(\frac{\epsilon}{10n}\bigg)^{\tau_0}\quad\text{for all }x\in \widetilde C.\end{align*} $$
Therefore,
![]() $\mathcal {I}_n$
is finite since elements in
$\mathcal {I}_n$
is finite since elements in
![]() $\mathcal {B}_n'$
are pairwise disjoint. Precisely,
$\mathcal {B}_n'$
are pairwise disjoint. Precisely,
 $$ \begin{align*}\sharp\mathcal{I}_n\le \bigg(\frac{10n}{\epsilon}\bigg)^{\tau_0}.\end{align*} $$
$$ \begin{align*}\sharp\mathcal{I}_n\le \bigg(\frac{10n}{\epsilon}\bigg)^{\tau_0}.\end{align*} $$
Now we put
 $$ \begin{align*}E_\epsilon=\bigg\{\bigg(x_i,e\bigg(\frac{\epsilon j}{4\pi}\bigg)\bigg):i\in\mathcal{I}_n \text{ and } j\in \bigg\{0,1,\ldots,\bigg[\frac{4\pi}{\epsilon}\bigg]\bigg\},\end{align*} $$
$$ \begin{align*}E_\epsilon=\bigg\{\bigg(x_i,e\bigg(\frac{\epsilon j}{4\pi}\bigg)\bigg):i\in\mathcal{I}_n \text{ and } j\in \bigg\{0,1,\ldots,\bigg[\frac{4\pi}{\epsilon}\bigg]\bigg\},\end{align*} $$
where
![]() $[{4\pi }/{\epsilon }]$
is the integer part of
$[{4\pi }/{\epsilon }]$
is the integer part of
![]() ${4\pi }/{\epsilon }$
. Then, for
${4\pi }/{\epsilon }$
. Then, for
![]() $n>{\epsilon }/{10r_\epsilon }$
, it is not hard to verify that
$n>{\epsilon }/{10r_\epsilon }$
, it is not hard to verify that
 $$ \begin{align*}B_{\bar d_n}\bigg(\bigg(x_i,e\bigg(\frac{\epsilon j}{4\pi}\bigg)\bigg),\epsilon\bigg) \supset B\bigg(x_i,\frac{\epsilon}{2n}\bigg)\times \bigg\{e(t):\bigg|t-\frac{\epsilon j}{4\pi}\bigg|<\frac{\epsilon}{4\pi}\bigg\}\end{align*} $$
$$ \begin{align*}B_{\bar d_n}\bigg(\bigg(x_i,e\bigg(\frac{\epsilon j}{4\pi}\bigg)\bigg),\epsilon\bigg) \supset B\bigg(x_i,\frac{\epsilon}{2n}\bigg)\times \bigg\{e(t):\bigg|t-\frac{\epsilon j}{4\pi}\bigg|<\frac{\epsilon}{4\pi}\bigg\}\end{align*} $$
for
![]() $i\in \mathcal {I}_n\text { and } j\in \{0,1,\ldots ,[{4\pi }/{\epsilon }]\}$
. This implies that for
$i\in \mathcal {I}_n\text { and } j\in \{0,1,\ldots ,[{4\pi }/{\epsilon }]\}$
. This implies that for
![]() $n>{\epsilon }/{10r_\epsilon }$
, one has
$n>{\epsilon }/{10r_\epsilon }$
, one has
 $$ \begin{align*} \rho\bigg(\bigcup_{y\in E_\epsilon}B_{\bar d_n}(y,\epsilon)\bigg)&\ge \rho\bigg(\bigcup_{i\in\mathcal{I}_n}B\bigg(x_i,\frac{\epsilon}{2n}\bigg)\times\mathbb{T}\bigg)=m\bigg(\bigcup_{i\in\mathcal{I}_n}B\bigg(x_i,\frac{\epsilon}{2n}\bigg)\bigg)\\ &\ge m( \widetilde C)\ge 1-\epsilon, \end{align*} $$
$$ \begin{align*} \rho\bigg(\bigcup_{y\in E_\epsilon}B_{\bar d_n}(y,\epsilon)\bigg)&\ge \rho\bigg(\bigcup_{i\in\mathcal{I}_n}B\bigg(x_i,\frac{\epsilon}{2n}\bigg)\times\mathbb{T}\bigg)=m\bigg(\bigcup_{i\in\mathcal{I}_n}B\bigg(x_i,\frac{\epsilon}{2n}\bigg)\bigg)\\ &\ge m( \widetilde C)\ge 1-\epsilon, \end{align*} $$
and
 $$ \begin{align*}S_n(d,T,\rho,\epsilon)\le \sharp E_\epsilon\le \sharp \mathcal{I}_n \times \frac{4\pi}{\epsilon }\le \bigg(\frac{10n}{\epsilon}\bigg)^{\tau_0}\times \frac{4\pi}{\epsilon }.\end{align*} $$
$$ \begin{align*}S_n(d,T,\rho,\epsilon)\le \sharp E_\epsilon\le \sharp \mathcal{I}_n \times \frac{4\pi}{\epsilon }\le \bigg(\frac{10n}{\epsilon}\bigg)^{\tau_0}\times \frac{4\pi}{\epsilon }.\end{align*} $$
By the fact
![]() $\tau _0<\tau $
, one has
$\tau _0<\tau $
, one has
This ends the proof of Lemma 3.3.
Now let
![]() $p=(0,0)$
be the origin of
$p=(0,0)$
be the origin of
![]() $\mathbb {C}$
. For a sequence
$\mathbb {C}$
. For a sequence
![]() $y\in (\mathbb {T}\cup \{ p\})^{\mathbb {Z}}$
, let
$y\in (\mathbb {T}\cup \{ p\})^{\mathbb {Z}}$
, let
 $$ \begin{align*}\mathrm{Gen}(y)=\bigg\{\mu\in\mathcal{M}((\mathbb{T} \cup\{p\})^{\mathbb{Z}},\sigma):\frac{1}{N_i-M_i}\sum_{M_i<n\le N_i}\delta_{\sigma^ny}\to\mu\text{ for }N_i-M_i\to+\infty\bigg\},\end{align*} $$
$$ \begin{align*}\mathrm{Gen}(y)=\bigg\{\mu\in\mathcal{M}((\mathbb{T} \cup\{p\})^{\mathbb{Z}},\sigma):\frac{1}{N_i-M_i}\sum_{M_i<n\le N_i}\delta_{\sigma^ny}\to\mu\text{ for }N_i-M_i\to+\infty\bigg\},\end{align*} $$
where
![]() $\sigma : (\mathbb {T}\cup \{p\})^{\mathbb {Z}}\rightarrow (\mathbb {T}\cup \{p\})^{\mathbb {Z}}$
is the left shift. Put
$\sigma : (\mathbb {T}\cup \{p\})^{\mathbb {Z}}\rightarrow (\mathbb {T}\cup \{p\})^{\mathbb {Z}}$
is the left shift. Put
![]() $X_y=\overline {\{\sigma ^ny:n\in \mathbb {Z}\}}$
. Then
$X_y=\overline {\{\sigma ^ny:n\in \mathbb {Z}\}}$
. Then
![]() $(X_y,\sigma )$
is a subsystem of
$(X_y,\sigma )$
is a subsystem of
![]() $((\mathbb {T}\cup \{p\})^{\mathbb {Z}},\sigma )$
. It is not hard to see that for
$((\mathbb {T}\cup \{p\})^{\mathbb {Z}},\sigma )$
. It is not hard to see that for
![]() $\mu \in \mathrm{Gen}(y)$
,
$\mu \in \mathrm{Gen}(y)$
,
![]() $\mu (X_y)=1$
, and thus we can identify
$\mu (X_y)=1$
, and thus we can identify
![]() $\mathrm{Gen}(y)$
with
$\mathrm{Gen}(y)$
with
![]() $\mathcal {M}(X_y,\sigma )$
. We have
$\mathcal {M}(X_y,\sigma )$
. We have
Lemma 3.4. Let C be a non-empty compact subset of
![]() $[0,1]$
and
$[0,1]$
and
![]() $y\in (\mathbb {T}\cup \{p\})^{\mathbb {Z}}$
. Assume that the pair
$y\in (\mathbb {T}\cup \{p\})^{\mathbb {Z}}$
. Assume that the pair
![]() $(y,C)$
meets the following property.
$(y,C)$
meets the following property.
Property
![]() $(*)$
—there exist
$(*)$
—there exist
![]() $\{m_1<n_1<m_2<n_2\ldots \}\subset \mathbb {Z}$
,
$\{m_1<n_1<m_2<n_2\ldots \}\subset \mathbb {Z}$
,
![]() $\{\theta _k\}_{k\ge 1}\subset C$
, and
$\{\theta _k\}_{k\ge 1}\subset C$
, and
![]() $\{\phi _k\}_{k\ge 1}\subset [0,1]$
such that:
$\{\phi _k\}_{k\ge 1}\subset [0,1]$
such that:
-
(1)
 $\lim _{i\to \infty }n_i-m_i=+\infty ;$
$\lim _{i\to \infty }n_i-m_i=+\infty ;$
-
(2)
 $y(j)=p$
for
$y(j)=p$
for
 $j\in \mathbb {Z}\setminus \bigcup _{i\in \mathbb {N}}[m_{i},n_{i});$
$j\in \mathbb {Z}\setminus \bigcup _{i\in \mathbb {N}}[m_{i},n_{i});$
-
(3)
 $y(m_i+j)=e(\phi _i+j\theta _i)$
for all
$y(m_i+j)=e(\phi _i+j\theta _i)$
for all
 $i\ge 1$
and
$i\ge 1$
and
 $0\le j< n_{i}-m_i$
.
$0\le j< n_{i}-m_i$
.
Then, any element in
![]() $\mathrm{Gen}(y)$
supports on the compact subset
$\mathrm{Gen}(y)$
supports on the compact subset
Proof. Assume that
![]() $(y,C)$
meets Property
$(y,C)$
meets Property
![]() $(*)$
and set
$(*)$
and set
It is clear that
![]() $X_y\setminus \bigcup _{n\in \mathbb {Z}}\sigma ^nZ\subset \widetilde {C}$
. To prove the lemma, it is enough to show that
$X_y\setminus \bigcup _{n\in \mathbb {Z}}\sigma ^nZ\subset \widetilde {C}$
. To prove the lemma, it is enough to show that
![]() $\mu (\widetilde C)=1$
for all
$\mu (\widetilde C)=1$
for all
![]() $\mu \in \mathrm{Gen}(y)$
. Since
$\mu \in \mathrm{Gen}(y)$
. Since
![]() $\mathrm{Gen}(y)=\mathcal {M}(X_y,\sigma )$
, it is enough to show that
$\mathrm{Gen}(y)=\mathcal {M}(X_y,\sigma )$
, it is enough to show that
![]() $\mu (Z)=0$
for all
$\mu (Z)=0$
for all
![]() $\mu \in \mathrm{Gen}(y)$
.
$\mu \in \mathrm{Gen}(y)$
.
Now we fix a
![]() $\mu \in \mathrm{Gen}(y)$
. Then there exist
$\mu \in \mathrm{Gen}(y)$
. Then there exist
![]() $M_1<N_1, M_2<N_2,\ldots $
such that
$M_1<N_1, M_2<N_2,\ldots $
such that
![]() $\lim _{i\rightarrow +\infty } N_i-M_i=+\infty $
and
$\lim _{i\rightarrow +\infty } N_i-M_i=+\infty $
and
 $$ \begin{align*}\lim_{i\rightarrow +\infty}\frac{1}{N_i-M_i}\sum_{M_i<n\le N_i}\delta_{\sigma^ny}=\mu.\end{align*} $$
$$ \begin{align*}\lim_{i\rightarrow +\infty}\frac{1}{N_i-M_i}\sum_{M_i<n\le N_i}\delta_{\sigma^ny}=\mu.\end{align*} $$
Since Z is an open subset of
![]() $(\mathbb {T}\cup \{p\})^{\mathbb {Z}}$
, we have
$(\mathbb {T}\cup \{p\})^{\mathbb {Z}}$
, we have
 $$ \begin{align*} \mu(Z)&\le \liminf_{i\rightarrow +\infty}\frac{1}{N_i-M_i}\sum_{M_i<n\le N_i}\delta_{\sigma^ny}(Z)\\ &=\liminf_{i\to +\infty}\frac{\sharp\{M_i<n\le N_i:\sigma^ny\in Z\}}{N_i-M_i}\\ &=\liminf_{i\to+\infty}\frac{\sharp\{M_i<n\le N_i:y(n-1)=p,y(n)\in\mathbb{T}\}}{N_i-M_i}\\ &=\liminf_{i\to+\infty}\frac{\sharp\{j\in\mathbb{N}: M_i<m_j\le N_i\}}{N_i-M_i} =0, \end{align*} $$
$$ \begin{align*} \mu(Z)&\le \liminf_{i\rightarrow +\infty}\frac{1}{N_i-M_i}\sum_{M_i<n\le N_i}\delta_{\sigma^ny}(Z)\\ &=\liminf_{i\to +\infty}\frac{\sharp\{M_i<n\le N_i:\sigma^ny\in Z\}}{N_i-M_i}\\ &=\liminf_{i\to+\infty}\frac{\sharp\{M_i<n\le N_i:y(n-1)=p,y(n)\in\mathbb{T}\}}{N_i-M_i}\\ &=\liminf_{i\to+\infty}\frac{\sharp\{j\in\mathbb{N}: M_i<m_j\le N_i\}}{N_i-M_i} =0, \end{align*} $$
where the last equality follows from Property
![]() $(*)$
(1). This ends the proof of Lemma 3.4.
$(*)$
(1). This ends the proof of Lemma 3.4.
The next lemma follows easily from the previous ones.
Lemma 3.5. Assume that
![]() $ C$
is a non-empty compact subset of
$ C$
is a non-empty compact subset of
![]() $[0,1]$
with
$[0,1]$
with
![]() $\mathrm{Dim}_P C<\tau $
and
$\mathrm{Dim}_P C<\tau $
and
![]() $y\in (\mathbb {T}\cup \{p\})^{\mathbb {Z}}$
. If
$y\in (\mathbb {T}\cup \{p\})^{\mathbb {Z}}$
. If
![]() $(y,C)$
meets Property
$(y,C)$
meets Property
![]() $(*)$
as in Lemma 3.4, then the t.d.s.
$(*)$
as in Lemma 3.4, then the t.d.s.
![]() $(X_y,\sigma )$
satisfies
$(X_y,\sigma )$
satisfies
for all
![]() $\epsilon>0$
and
$\epsilon>0$
and
![]() $\rho \in \mathcal {M}(X_y,\sigma )$
.
$\rho \in \mathcal {M}(X_y,\sigma )$
.
Proof. Fix a pair
![]() $(y,C)$
which meets Property
$(y,C)$
which meets Property
![]() $(*)$
as in Lemma 3.4. Then all measures in
$(*)$
as in Lemma 3.4. Then all measures in
![]() $\mathrm{Gen}(y)$
support on a compact set,
$\mathrm{Gen}(y)$
support on a compact set,
It is clear that
![]() $\widetilde {C}$
is a
$\widetilde {C}$
is a
![]() $\sigma $
-invariant compact subset of
$\sigma $
-invariant compact subset of
![]() $(\mathbb {T}\cup \{p\})^{\mathbb {Z}}$
, that is,
$(\mathbb {T}\cup \{p\})^{\mathbb {Z}}$
, that is,
![]() $(\widetilde C,\sigma )$
is a t.d.s. Notice that
$(\widetilde C,\sigma )$
is a t.d.s. Notice that
![]() $(\widetilde C,\sigma )$
is a factor of
$(\widetilde C,\sigma )$
is a factor of
![]() $(C\times \mathbb {T}\cup \{p\},T)$
, where
$(C\times \mathbb {T}\cup \{p\},T)$
, where
![]() $T: C\times \mathbb {T}\cup \{p\} \to C\times \mathbb {T}\cup \{p\}$
with
$T: C\times \mathbb {T}\cup \{p\} \to C\times \mathbb {T}\cup \{p\}$
with
![]() $T(p)=p$
and
$T(p)=p$
and
![]() $T(x,e(y))= (x,e(y+x))$
for
$T(x,e(y))= (x,e(y+x))$
for
![]() $(x,e(y))\in C\times \mathbb {T}$
. The lemma is immediately from Lemma 3.3.
$(x,e(y))\in C\times \mathbb {T}$
. The lemma is immediately from Lemma 3.3.
The final lemma we need is the following one.
Lemma 3.6. If there exist a non-empty compact subset C of
![]() $[0,1]$
and
$[0,1]$
and
![]() $\beta \in \mathbb {R}$
such that
$\beta \in \mathbb {R}$
such that
then there is
![]() $y\in (\mathbb {T}\cup \{p\})^{\mathbb {Z}}$
such that
$y\in (\mathbb {T}\cup \{p\})^{\mathbb {Z}}$
such that
![]() $(y,C)$
meets Property
$(y,C)$
meets Property
![]() $(*)$
as in Lemma 3.4 and
$(*)$
as in Lemma 3.4 and
where
![]() $\widetilde F: (\mathbb {T}\cup \{p\})^{\mathbb {Z}}\to \mathbb {C}$
is the continuous function defined by
$\widetilde F: (\mathbb {T}\cup \{p\})^{\mathbb {Z}}\to \mathbb {C}$
is the continuous function defined by
![]() $\widetilde F( z)=z(0)$
if
$\widetilde F( z)=z(0)$
if
![]() $z(0)\in \mathbb {T}$
and
$z(0)\in \mathbb {T}$
and
![]() $0$
if
$0$
if
![]() $z(0)=p$
.
$z(0)=p$
.
Proof. By the assumption in equation (3.1) and the similar arguments as in the proof of Theorem 1.1 (2)
![]() $\Longrightarrow $
(1), we can find
$\Longrightarrow $
(1), we can find
![]() $\tau \in (0,1)$
, strictly increasing sequences
$\tau \in (0,1)$
, strictly increasing sequences
![]() $\{H_i\}_{i\in \mathbb {N}},\{N_i\}_{i\in \mathbb {N}}$
of natural numbers, series
$\{H_i\}_{i\in \mathbb {N}},\{N_i\}_{i\in \mathbb {N}}$
of natural numbers, series
![]() $\{\alpha _{i,j}\}_{j=1}^{N_i}\subset \mathbb {R}$
,
$\{\alpha _{i,j}\}_{j=1}^{N_i}\subset \mathbb {R}$
,
![]() $i=1,2,3\ldots, $
and
$i=1,2,3\ldots, $
and
![]() $\beta \in \{0,\tfrac 14,\tfrac 24,\tfrac 34\}$
such that for each
$\beta \in \{0,\tfrac 14,\tfrac 24,\tfrac 34\}$
such that for each
![]() $i\in \mathbb {N}$
, one has
$i\in \mathbb {N}$
, one has
and
For
![]() $i\in \mathbb {N}$
, let
$i\in \mathbb {N}$
, let
![]() $M_i=\sum _{n=1}^{N_i}({1}/{n})$
and
$M_i=\sum _{n=1}^{N_i}({1}/{n})$
and
 $$ \begin{align} S_i=\bigg\{n\in[1,N_i]:\mathrm{Re}(e(\beta) \mathbb{E}_{h\le H_i}\mu (n + h)e(h\alpha_{n,i}))>\frac{\tau}{2}\bigg\}.\end{align} $$
$$ \begin{align} S_i=\bigg\{n\in[1,N_i]:\mathrm{Re}(e(\beta) \mathbb{E}_{h\le H_i}\mu (n + h)e(h\alpha_{n,i}))>\frac{\tau}{2}\bigg\}.\end{align} $$
Then by equation (3.4), one has
 $$ \begin{align} \sum_{n\in S_i}\frac{1}{n}>\frac{\tau}{2}M_i. \end{align} $$
$$ \begin{align} \sum_{n\in S_i}\frac{1}{n}>\frac{\tau}{2}M_i. \end{align} $$
Notice that
![]() $\lim _{N\to +\infty }({\sum _{n\le N^\sigma }({1}/{n})}/{\sum _{n\le N}({1}/{n})})=\sigma .$
We have
$\lim _{N\to +\infty }({\sum _{n\le N^\sigma }({1}/{n})}/{\sum _{n\le N}({1}/{n})})=\sigma .$
We have
 $$ \begin{align*}\sum_{n\in S_i\setminus[1,N_{i}^\sigma]}\frac{1}{n}\overset{(3.6)}>\frac{\tau}{2}M_i-\sum_{n\le N_{i}^\sigma}\frac{1}{n}>\frac{\tau}{2}M_i-2\sigma M_{i-1}\overset{(3.3)}>\frac{\tau}{4}M_i \end{align*} $$
$$ \begin{align*}\sum_{n\in S_i\setminus[1,N_{i}^\sigma]}\frac{1}{n}\overset{(3.6)}>\frac{\tau}{2}M_i-\sum_{n\le N_{i}^\sigma}\frac{1}{n}>\frac{\tau}{2}M_i-2\sigma M_{i-1}\overset{(3.3)}>\frac{\tau}{4}M_i \end{align*} $$
for
![]() $i\in \mathbb {N}$
large enough. Then we can choose
$i\in \mathbb {N}$
large enough. Then we can choose
![]() $S_i'\subset S_i\setminus [1,N_{i}^\sigma ]$
such that each gap in
$S_i'\subset S_i\setminus [1,N_{i}^\sigma ]$
such that each gap in
![]() $S_i'$
is not less than
$S_i'$
is not less than
![]() $2H_i$
and
$2H_i$
and
 $$ \begin{align}\sum_{n\in S^{\prime}_i}\frac{1}{n}> \frac{\tau M_i}{8H_i}\end{align} $$
$$ \begin{align}\sum_{n\in S^{\prime}_i}\frac{1}{n}> \frac{\tau M_i}{8H_i}\end{align} $$
for
![]() $i\in \mathbb {N}$
large enough. Define
$i\in \mathbb {N}$
large enough. Define
![]() $y: \mathbb {Z}\to \mathbb {T}\cup \{p\}$
such that
$y: \mathbb {Z}\to \mathbb {T}\cup \{p\}$
such that
and
![]() $y(j)=p$
for other j, where p is the zero of
$y(j)=p$
for other j, where p is the zero of
![]() $\mathbb {C}$
. It is not hard to see that y is well defined and meets Property
$\mathbb {C}$
. It is not hard to see that y is well defined and meets Property
![]() $(*)$
.
$(*)$
.
Now we are going to show that equation (3.2) holds. Combining equations (3.5) with (3.7), one has
 $$ \begin{align} \mathrm{Re}\bigg(e(\beta)\sum_{n\in S_i'}\sum_{h\le H_i}\frac{\mu (n + h) \widetilde F(\sigma^{n+h}y) }{n}\bigg)>\frac{\tau}{2}\times H_i\times\sum_{n\in S_i'}\frac{1}{n}>\frac{\tau^2}{16}M_i \end{align} $$
$$ \begin{align} \mathrm{Re}\bigg(e(\beta)\sum_{n\in S_i'}\sum_{h\le H_i}\frac{\mu (n + h) \widetilde F(\sigma^{n+h}y) }{n}\bigg)>\frac{\tau}{2}\times H_i\times\sum_{n\in S_i'}\frac{1}{n}>\frac{\tau^2}{16}M_i \end{align} $$
for
![]() $i\in \mathbb {N}$
large enough. Then,
$i\in \mathbb {N}$
large enough. Then,
 $$ \begin{align*}&\bigg|\sum_{n\in S_i'}\sum_{h\le H_i}\frac{\mu(n+h)\widetilde F(\sigma^{n+h}y)}{n}-\sum_{n\in S_i'}\sum_{h\le H_i}\frac{\mu(n+h)\widetilde F(\sigma^{n+h}y)}{n+h}\bigg|\\ &\quad\le \sum_{n\in S_i'} \sum_{h\le H_i}(\frac{1}{n}-\frac{1}{n+h})\le \sum_{n\in S_i'} \sum_{h\le H_i}\frac{H_i}{n(n+H_i)}\\ &\quad\le \sum_{n\in S_i'} \frac{H_i}{nN_i^\sigma} \overset{(3.3)}\le \sigma\sum_{n\in S_i'}\frac{1}{n}\overset{(3.3)}\le \frac{\tau^2}{32}M_i \end{align*} $$
$$ \begin{align*}&\bigg|\sum_{n\in S_i'}\sum_{h\le H_i}\frac{\mu(n+h)\widetilde F(\sigma^{n+h}y)}{n}-\sum_{n\in S_i'}\sum_{h\le H_i}\frac{\mu(n+h)\widetilde F(\sigma^{n+h}y)}{n+h}\bigg|\\ &\quad\le \sum_{n\in S_i'} \sum_{h\le H_i}(\frac{1}{n}-\frac{1}{n+h})\le \sum_{n\in S_i'} \sum_{h\le H_i}\frac{H_i}{n(n+H_i)}\\ &\quad\le \sum_{n\in S_i'} \frac{H_i}{nN_i^\sigma} \overset{(3.3)}\le \sigma\sum_{n\in S_i'}\frac{1}{n}\overset{(3.3)}\le \frac{\tau^2}{32}M_i \end{align*} $$
for
![]() $i\in \mathbb {N}$
large enough. Combining this inequality with equation (3.8), one has
$i\in \mathbb {N}$
large enough. Combining this inequality with equation (3.8), one has
 $$ \begin{align*}\bigg|\sum_{N_{i}^\sigma<n\le N_i+H_i}\frac{\mu (n )\widetilde F(\sigma^{n}y)}{n}\bigg|&=\bigg|\sum_{n\in S_i'}\sum_{h\le H_i}\frac{\mu(n+h)\widetilde F(\sigma^{n+h}y)}{n+h}\bigg|\\ &\ge \mathrm{Re}\bigg(e(\beta)\sum_{n\in S_i'}\sum_{h\le H_i}\frac{\mu (n + h)y(n+h)}{n}\bigg)-\frac{\tau^2M_i}{32}\\ &\ge \frac{\tau^2M_i}{32} \end{align*} $$
$$ \begin{align*}\bigg|\sum_{N_{i}^\sigma<n\le N_i+H_i}\frac{\mu (n )\widetilde F(\sigma^{n}y)}{n}\bigg|&=\bigg|\sum_{n\in S_i'}\sum_{h\le H_i}\frac{\mu(n+h)\widetilde F(\sigma^{n+h}y)}{n+h}\bigg|\\ &\ge \mathrm{Re}\bigg(e(\beta)\sum_{n\in S_i'}\sum_{h\le H_i}\frac{\mu (n + h)y(n+h)}{n}\bigg)-\frac{\tau^2M_i}{32}\\ &\ge \frac{\tau^2M_i}{32} \end{align*} $$
for
![]() $i\in \mathbb {N}$
large enough. Thus,
$i\in \mathbb {N}$
large enough. Thus,
 $$ \begin{align*}|\mathbb{E}_{n\le N_i}^{\log} \mu (n)\widetilde F(\sigma^ny)|&\ge\bigg|\frac{1}{M_i}\sum_{n\le N_i+H_i}\frac{\mu (n ) \widetilde F(\sigma^ny)}{n}\bigg|-\frac{1}{M_i}\sum_{N_i<n\le N_i+H_i\text{ or }\atop n \le N_{i}^\sigma}\bigg|\frac{\mu (n )\widetilde F(\sigma^ny)}{n}\bigg|\\ &\ge \frac{\tau^2}{32}-2\sigma-\frac{H_i}{N_i}\overset{(3.3)}\ge\frac{\tau^2}{100}>0 \end{align*} $$
$$ \begin{align*}|\mathbb{E}_{n\le N_i}^{\log} \mu (n)\widetilde F(\sigma^ny)|&\ge\bigg|\frac{1}{M_i}\sum_{n\le N_i+H_i}\frac{\mu (n ) \widetilde F(\sigma^ny)}{n}\bigg|-\frac{1}{M_i}\sum_{N_i<n\le N_i+H_i\text{ or }\atop n \le N_{i}^\sigma}\bigg|\frac{\mu (n )\widetilde F(\sigma^ny)}{n}\bigg|\\ &\ge \frac{\tau^2}{32}-2\sigma-\frac{H_i}{N_i}\overset{(3.3)}\ge\frac{\tau^2}{100}>0 \end{align*} $$
for
![]() $i\in \mathbb {N}$
large enough. Therefore, y is the point as required. This ends the proof of Lemma 3.6.
$i\in \mathbb {N}$
large enough. Therefore, y is the point as required. This ends the proof of Lemma 3.6.
Now we are ready to prove Theorem 1.3.
Proof of Theorem 1.3
Assume that Theorem 1.3 is not valid. Then there exists a non-empty compact subset C of
![]() $[0,1]$
with
$[0,1]$
with
![]() $\mathrm{Dim}_P C<1$
such that
$\mathrm{Dim}_P C<1$
such that
Thus, we can find
![]() $\beta \in \{0,\tfrac 14,\tfrac 24,\tfrac 34\}$
such that
$\beta \in \{0,\tfrac 14,\tfrac 24,\tfrac 34\}$
such that
By Lemma 3.6, there is
![]() $y\in (\mathbb {T}\cup \{p\})^{\mathbb {Z}}$
such that
$y\in (\mathbb {T}\cup \{p\})^{\mathbb {Z}}$
such that
![]() $(y,C)$
meets Property
$(y,C)$
meets Property
![]() $(*)$
as in Lemma 3.4 and
$(*)$
as in Lemma 3.4 and
where
![]() $\widetilde F: X_y\to \mathbb {R}$
is a continuous function defined by
$\widetilde F: X_y\to \mathbb {R}$
is a continuous function defined by
![]() $\widetilde F(z)=z(0)$
if
$\widetilde F(z)=z(0)$
if
![]() $z(0)\in \mathbb {T}$
and
$z(0)\in \mathbb {T}$
and
![]() $0$
if
$0$
if
![]() $z(0)=p$
. Then, by Lemma 3.5 and the assumption
$z(0)=p$
. Then, by Lemma 3.5 and the assumption
![]() $\mathrm{Dim}_P C<1$
, the t.d.s.
$\mathrm{Dim}_P C<1$
, the t.d.s.
![]() $(X_y,\sigma )$
satisfies
$(X_y,\sigma )$
satisfies
By Theorem 1.2,
This conflicts with equation (3.9) and the theorem follows. We end the proof of Theorem 1.3.
Acknowledgements
W.H. was partially supported by NNSF of China (12090012, 12031019, 11731003); L.X. was partially supported by NNSF of China (12031019, 11871188) and USTC Research Funds of the Double First-Class Initiative; and X.Y. was partially supported by NNSF of China (12031019).
A Appendix. Proof of Theorem 1.2
In this appendix, we prove Theorem 1.2 following the arguments of the proof of [Reference Huang, Wang and Ye11, Theorem 1.1’].
Let
![]() $(X,T)$
be a t.d.s. with a metric d and sub-linear mean measure complexity. To prove that the logarithmic Sarnak conjecture holds for
$(X,T)$
be a t.d.s. with a metric d and sub-linear mean measure complexity. To prove that the logarithmic Sarnak conjecture holds for
![]() $(X,T)$
, it is sufficient to show
$(X,T)$
, it is sufficient to show
 $$ \begin{align} \limsup_{i\rightarrow +\infty}\bigg|\frac{1}{\sum_{n=1}^{N_i} ({1}/{n}) } \sum_{n=1}^{N_i} \frac{\mu(n)f(T^nx)}{n}\bigg|<7\epsilon \end{align} $$
$$ \begin{align} \limsup_{i\rightarrow +\infty}\bigg|\frac{1}{\sum_{n=1}^{N_i} ({1}/{n}) } \sum_{n=1}^{N_i} \frac{\mu(n)f(T^nx)}{n}\bigg|<7\epsilon \end{align} $$
for any
![]() $\epsilon \in (0,1)$
and
$\epsilon \in (0,1)$
and
![]() $f\in C(X)$
with
$f\in C(X)$
with
![]() $\max _{z\in X}|f(z)|\le 1$
,
$\max _{z\in X}|f(z)|\le 1$
,
![]() $x\in X$
and
$x\in X$
and
![]() $\{ N_1<N_2<N_3<\cdots \} \subseteq \mathbb {N}$
such that the sequence
$\{ N_1<N_2<N_3<\cdots \} \subseteq \mathbb {N}$
such that the sequence
![]() $\mathbb {E}^{\log }_{n\le N_i}\delta _{T^nx}$
weakly
$\mathbb {E}^{\log }_{n\le N_i}\delta _{T^nx}$
weakly
![]() $^*$
converges to a Borel probability measure
$^*$
converges to a Borel probability measure
![]() $\rho $
.
$\rho $
.
To this aim, we will find
![]() $L\in \mathbb {N}$
,
$L\in \mathbb {N}$
,
![]() $\{x_1,x_2,\ldots ,x_m\}\subset X$
and
$\{x_1,x_2,\ldots ,x_m\}\subset X$
and
![]() $j_n\in \{1,2,\ldots ,m\}$
for
$j_n\in \{1,2,\ldots ,m\}$
for
![]() $n=1,2,3,\ldots $
such that that for large i,
$n=1,2,3,\ldots $
such that that for large i,
 $$ \begin{align} \bigg|\frac{1}{M_i}\sum_{n=1}^{N_i} \frac{\mu(n)f(T^nx)}{n}-\frac{1}{M_i}\sum_{n=1}^{N_i} \bigg( \frac{1}{L} \sum_{\ell=0}^{L-1} \frac{\mu(n+\ell) f(T^\ell x_{j_n})}{n}\bigg)\bigg|<5\epsilon \end{align} $$
$$ \begin{align} \bigg|\frac{1}{M_i}\sum_{n=1}^{N_i} \frac{\mu(n)f(T^nx)}{n}-\frac{1}{M_i}\sum_{n=1}^{N_i} \bigg( \frac{1}{L} \sum_{\ell=0}^{L-1} \frac{\mu(n+\ell) f(T^\ell x_{j_n})}{n}\bigg)\bigg|<5\epsilon \end{align} $$
and
 $$ \begin{align} \bigg|\frac{1}{M_i}\sum_{n=1}^{N_i} \bigg( \frac{1}{L}\sum_{\ell=0}^{L-1} \frac{\mu(n+\ell) f(T^\ell x_{j_n})}{n}\bigg)\bigg|<2\epsilon. \end{align} $$
$$ \begin{align} \bigg|\frac{1}{M_i}\sum_{n=1}^{N_i} \bigg( \frac{1}{L}\sum_{\ell=0}^{L-1} \frac{\mu(n+\ell) f(T^\ell x_{j_n})}{n}\bigg)\bigg|<2\epsilon. \end{align} $$
It is clear that equation (A.1) follows by equations (A.2) and (A.3). Equations (A.2) and (A.3) will be proved in Lemmas A.1 and A.2) respectively, where we write
![]() $M_i= \sum _{n=1}^{N_i} (1/n)$
for
$M_i= \sum _{n=1}^{N_i} (1/n)$
for
![]() $i\in \mathbb {N}$
.
$i\in \mathbb {N}$
.
To prove the two lemmas, we first choose
![]() $\epsilon _1>0$
such that
$\epsilon _1>0$
such that
![]() $\epsilon _1<\epsilon ^2$
and
$\epsilon _1<\epsilon ^2$
and
Since
![]() $\mathbb {E}^{\log }_{n\le N_i}\delta _{T^nx}$
weakly
$\mathbb {E}^{\log }_{n\le N_i}\delta _{T^nx}$
weakly
![]() $^*$
converges to
$^*$
converges to
![]() $\rho $
, it is not hard to verify
$\rho $
, it is not hard to verify
![]() $\rho \in \mathcal {M}(X,T)$
. So, the measure complexity of
$\rho \in \mathcal {M}(X,T)$
. So, the measure complexity of
![]() $(X,d,T,\rho )$
is sub-linear by the assumption of the theorem, and thus there exists
$(X,d,T,\rho )$
is sub-linear by the assumption of the theorem, and thus there exists
![]() $L>0$
such that
$L>0$
such that
This means that there exist
![]() $x_1,x_2,\ldots ,x_m\in X$
such that
$x_1,x_2,\ldots ,x_m\in X$
such that
 $$ \begin{align*}\rho\big(\bigcup_{i=1}^m B_{\overline{d}_L}(x_i,\epsilon_1)\big)>1-\epsilon_1>1-\epsilon^2.\end{align*} $$
$$ \begin{align*}\rho\big(\bigcup_{i=1}^m B_{\overline{d}_L}(x_i,\epsilon_1)\big)>1-\epsilon_1>1-\epsilon^2.\end{align*} $$
Put
![]() $U=\bigcup _{i=1}^m B_{\overline {d}_L}(x_i,\epsilon _1)$
and
$U=\bigcup _{i=1}^m B_{\overline {d}_L}(x_i,\epsilon _1)$
and
![]() $E=\{n\in \mathbb {N}:T^n x\in U\}$
. Then U is open and so
$E=\{n\in \mathbb {N}:T^n x\in U\}$
. Then U is open and so
 $$ \begin{align} \liminf_{i\rightarrow +\infty}\frac{1}{M_i}\sum_{n\in E\cap [1,N_i]}\frac{1}{n} =\liminf_{i\rightarrow +\infty}\frac{1}{M_i}\sum_{n=1}^{N_i} \frac{\delta_{T^nx}(U)}{n}\ge \rho(U)>1-\epsilon_1. \end{align} $$
$$ \begin{align} \liminf_{i\rightarrow +\infty}\frac{1}{M_i}\sum_{n\in E\cap [1,N_i]}\frac{1}{n} =\liminf_{i\rightarrow +\infty}\frac{1}{M_i}\sum_{n=1}^{N_i} \frac{\delta_{T^nx}(U)}{n}\ge \rho(U)>1-\epsilon_1. \end{align} $$
For
![]() $n\in E$
, we choose
$n\in E$
, we choose
![]() $j_n\in \{1,2,\ldots ,m\}$
such that
$j_n\in \{1,2,\ldots ,m\}$
such that
![]() $T^nx\in B_{\overline {d}_L}(x_{j_n},\epsilon _1)$
. Hence, for
$T^nx\in B_{\overline {d}_L}(x_{j_n},\epsilon _1)$
. Hence, for
![]() $n\in E$
, we have
$n\in E$
, we have
![]() $\overline {d}_L(T^nx,x_{j_n})<\epsilon _1$
, that is,
$\overline {d}_L(T^nx,x_{j_n})<\epsilon _1$
, that is,
 $$ \begin{align*}\frac{1}{L}\sum_{\ell=0}^{L-1} d\big( T^\ell(T^nx),T^\ell(x_{j_n})\big)<\epsilon_1,\end{align*} $$
$$ \begin{align*}\frac{1}{L}\sum_{\ell=0}^{L-1} d\big( T^\ell(T^nx),T^\ell(x_{j_n})\big)<\epsilon_1,\end{align*} $$
and so we have
Thus, for
![]() $n\in E$
,
$n\in E$
,
 $$ \begin{align} &\frac{1}{L} \sum_{\ell=0}^{L-1} |f(T^{\ell} (T^n x) )-f(T^\ell x_{j_n})|\nonumber\\ &\quad\le \frac{1}{L} \big(\epsilon\#\{\ell\in [0,L-1]:d(T^{\ell} (T^n x),T^{\ell}x_{j_n})<\sqrt{\epsilon_1}\}\\ &\qquad\qquad+2\#\{\ell\in [0,L-1]:d(T^{\ell} (T^n x),T^{\ell}x_{j_n})\ge \sqrt{\epsilon_1}\}\big)\nonumber \\ &\quad<3\epsilon \nonumber, \end{align} $$
$$ \begin{align} &\frac{1}{L} \sum_{\ell=0}^{L-1} |f(T^{\ell} (T^n x) )-f(T^\ell x_{j_n})|\nonumber\\ &\quad\le \frac{1}{L} \big(\epsilon\#\{\ell\in [0,L-1]:d(T^{\ell} (T^n x),T^{\ell}x_{j_n})<\sqrt{\epsilon_1}\}\\ &\qquad\qquad+2\#\{\ell\in [0,L-1]:d(T^{\ell} (T^n x),T^{\ell}x_{j_n})\ge \sqrt{\epsilon_1}\}\big)\nonumber \\ &\quad<3\epsilon \nonumber, \end{align} $$
by using the inequality in equation A.4, equation (A.7), and the assumption
![]() $\max _{x\in X}|f(x)| \le 1$
.
$\max _{x\in X}|f(x)| \le 1$
.
For each
![]() $n\notin E$
, we simply set
$n\notin E$
, we simply set
![]() $j_n=1$
.
$j_n=1$
.
We first establish Lemma A.1.
Lemma A.1. For all sufficiently large i,
 $$ \begin{align*}\bigg|\frac{1}{M_i}\sum_{n=1}^{N_i} \frac{\mu(n)f(T^nx)}{n}-\frac{1}{M_i}\sum_{n=1}^{N_i} \frac{1}{L} \sum_{\ell=0}^{L-1}\frac{ \mu(n+\ell) f(T^\ell x_{j_n})}{n} \bigg|<5\epsilon.\end{align*} $$
$$ \begin{align*}\bigg|\frac{1}{M_i}\sum_{n=1}^{N_i} \frac{\mu(n)f(T^nx)}{n}-\frac{1}{M_i}\sum_{n=1}^{N_i} \frac{1}{L} \sum_{\ell=0}^{L-1}\frac{ \mu(n+\ell) f(T^\ell x_{j_n})}{n} \bigg|<5\epsilon.\end{align*} $$
Proof. As
![]() $\max _{x\in X}|f(x)|\le 1$
, it is not hard to see that
$\max _{x\in X}|f(x)|\le 1$
, it is not hard to see that
 $$ \begin{align} \limsup_{i\to+\infty}\bigg|\frac{1}{M_i}\sum_{n=1}^{N_i} \frac{\mu(n)f(T^nx)}{n}-\frac{1}{M_i}\sum_{n=1}^{N_i} \frac{1}{L} \sum_{\ell=0}^{L-1} \frac{\mu(n+\ell) f(T^{n+\ell} x)}{n} \bigg| =0. \end{align} $$
$$ \begin{align} \limsup_{i\to+\infty}\bigg|\frac{1}{M_i}\sum_{n=1}^{N_i} \frac{\mu(n)f(T^nx)}{n}-\frac{1}{M_i}\sum_{n=1}^{N_i} \frac{1}{L} \sum_{\ell=0}^{L-1} \frac{\mu(n+\ell) f(T^{n+\ell} x)}{n} \bigg| =0. \end{align} $$
By equation (A.6), once i is large enough,
 $$ \begin{align} \frac{1}{M_i}\sum_{n\in E\cap [1,N_i]}\frac{1}{n}>1-\epsilon^2>1-\epsilon. \end{align} $$
$$ \begin{align} \frac{1}{M_i}\sum_{n\in E\cap [1,N_i]}\frac{1}{n}>1-\epsilon^2>1-\epsilon. \end{align} $$
Now,
 $$ \begin{align*} &\bigg|\frac{1}{M_i}\sum_{n=1}^{N_i} \frac{1}{L} \sum_{\ell=0}^{L-1} \frac{\mu(n+\ell) f(T^{n+\ell} x)}{n} - \frac{1}{M_i}\sum_{n=1}^{N_i} \frac{1}{L} \sum_{\ell=0}^{L-1} \frac{\mu(n+\ell) f(T^{\ell} x_{j_n})}{n} \bigg|\\ &\quad\le \frac{1}{M_i}\sum_{n=1}^{N_i} \frac{1}{L} \sum_{\ell=0}^{L-1} \frac{|f(T^{\ell} (T^n x) )-f(T^\ell x_{j_n})|}{n}\\ &\quad\le \frac{1}{M_i}\sum_{n\in [1,N_i]\setminus E} \frac{1}{L} \sum_{\ell=0}^{L-1} \frac{|f(T^{\ell} (T^n x) )-f(T^\ell x_{j_n})|}{n}\\ &\qquad+\frac{1}{M_i}\sum_{n\in E\cap [1,N_i]} \frac{1}{L} \sum_{\ell=0}^{L-1} \frac{|f(T^{\ell} (T^n x) )-f(T^\ell x_{j_n})|}{n}\\ &\quad<\frac{2}{M_i}\sum_{n\in [1,N_i]\setminus E}\frac{1}{n}+\frac{3\epsilon}{M_i}\sum_{n\in E\cap [1,N_i]}\frac{1}{n} \ \ \ \text{ (by equation}~({\text{A}.8}))\\ &\quad< \frac{2}{M_i}\sum_{n\in [1,N_i]\setminus E}\frac{1}{n}+3\epsilon. \end{align*} $$
$$ \begin{align*} &\bigg|\frac{1}{M_i}\sum_{n=1}^{N_i} \frac{1}{L} \sum_{\ell=0}^{L-1} \frac{\mu(n+\ell) f(T^{n+\ell} x)}{n} - \frac{1}{M_i}\sum_{n=1}^{N_i} \frac{1}{L} \sum_{\ell=0}^{L-1} \frac{\mu(n+\ell) f(T^{\ell} x_{j_n})}{n} \bigg|\\ &\quad\le \frac{1}{M_i}\sum_{n=1}^{N_i} \frac{1}{L} \sum_{\ell=0}^{L-1} \frac{|f(T^{\ell} (T^n x) )-f(T^\ell x_{j_n})|}{n}\\ &\quad\le \frac{1}{M_i}\sum_{n\in [1,N_i]\setminus E} \frac{1}{L} \sum_{\ell=0}^{L-1} \frac{|f(T^{\ell} (T^n x) )-f(T^\ell x_{j_n})|}{n}\\ &\qquad+\frac{1}{M_i}\sum_{n\in E\cap [1,N_i]} \frac{1}{L} \sum_{\ell=0}^{L-1} \frac{|f(T^{\ell} (T^n x) )-f(T^\ell x_{j_n})|}{n}\\ &\quad<\frac{2}{M_i}\sum_{n\in [1,N_i]\setminus E}\frac{1}{n}+\frac{3\epsilon}{M_i}\sum_{n\in E\cap [1,N_i]}\frac{1}{n} \ \ \ \text{ (by equation}~({\text{A}.8}))\\ &\quad< \frac{2}{M_i}\sum_{n\in [1,N_i]\setminus E}\frac{1}{n}+3\epsilon. \end{align*} $$
Combining this inequality with equation (A.10), when i is large enough,
 $$ \begin{align} \begin{split} &\bigg|\frac{1}{M_i}\sum_{n=1}^{N_i} \frac{1}{L} \sum_{\ell=0}^{L-1} \frac{\mu(n+\ell) f(T^{n+\ell} x)}{n} - \frac{1}{M_i}\sum_{n=1}^{N_i} \frac{1}{L} \sum_{\ell=0}^{L-1} \frac{\mu(n+\ell) f(T^{\ell} x_{j_n})}{n} \bigg| \\ &\quad< 5\epsilon. \end{split} \end{align} $$
$$ \begin{align} \begin{split} &\bigg|\frac{1}{M_i}\sum_{n=1}^{N_i} \frac{1}{L} \sum_{\ell=0}^{L-1} \frac{\mu(n+\ell) f(T^{n+\ell} x)}{n} - \frac{1}{M_i}\sum_{n=1}^{N_i} \frac{1}{L} \sum_{\ell=0}^{L-1} \frac{\mu(n+\ell) f(T^{\ell} x_{j_n})}{n} \bigg| \\ &\quad< 5\epsilon. \end{split} \end{align} $$
So the lemma follows by equations (A.9) and (A.11). This ends the proof of Lemma A.1.
Now we proceed to show Lemma A.2.
Lemma A.2. For all sufficiently large i,
 $$ \begin{align*}\bigg|\frac{1}{M_i}\sum_{n=1}^{N_i} \frac{1}{L} \sum_{\ell=0}^{L-1} \frac{\mu(n+\ell) f(T^\ell x_{j_n})}{n} \bigg|< 2\epsilon.\end{align*} $$
$$ \begin{align*}\bigg|\frac{1}{M_i}\sum_{n=1}^{N_i} \frac{1}{L} \sum_{\ell=0}^{L-1} \frac{\mu(n+\ell) f(T^\ell x_{j_n})}{n} \bigg|< 2\epsilon.\end{align*} $$
Proof. By Cauchy’s inequality,
 $$ \begin{align*} &\bigg|\frac{1}{M_i}\sum_{n=1}^{N_i} \frac{1}{L} \sum_{\ell=0}^{L-1}\frac{ \mu(n+\ell) f(T^\ell x_{j_n}) }{n} \bigg|^2\\&\quad\le \frac{1}{M_i}\sum_{n=1}^{N_i}\frac{1}{n}\bigg |\frac{1}{L} \sum_{\ell=0}^{L-1} \mu(n+\ell) f(T^\ell x_{j_n}) \bigg|^2\\&\quad\le \frac{1}{M_i}\sum_{n=1}^{N_i}\frac{1}{n}\sum_{j=1}^m\bigg |\frac{1}{L} \sum_{\ell=0}^{L-1} \mu(n+\ell) f(T^\ell x_{j}) \bigg|^2\\&\quad\le \frac{1}{L^2}\sum_{j=1}^m\sum_{\ell_1=0}^{L-1}\sum_{\ell_2=0}^{L-1}\frac{f(T^{\ell_1}x_j) \overline{f}(T^{\ell_2}x_j)}{M_i}\sum_{n=1}^{N_i}\frac{\mu(n+\ell_1)\mu(n+\ell_2)}{n}. \end{align*} $$
$$ \begin{align*} &\bigg|\frac{1}{M_i}\sum_{n=1}^{N_i} \frac{1}{L} \sum_{\ell=0}^{L-1}\frac{ \mu(n+\ell) f(T^\ell x_{j_n}) }{n} \bigg|^2\\&\quad\le \frac{1}{M_i}\sum_{n=1}^{N_i}\frac{1}{n}\bigg |\frac{1}{L} \sum_{\ell=0}^{L-1} \mu(n+\ell) f(T^\ell x_{j_n}) \bigg|^2\\&\quad\le \frac{1}{M_i}\sum_{n=1}^{N_i}\frac{1}{n}\sum_{j=1}^m\bigg |\frac{1}{L} \sum_{\ell=0}^{L-1} \mu(n+\ell) f(T^\ell x_{j}) \bigg|^2\\&\quad\le \frac{1}{L^2}\sum_{j=1}^m\sum_{\ell_1=0}^{L-1}\sum_{\ell_2=0}^{L-1}\frac{f(T^{\ell_1}x_j) \overline{f}(T^{\ell_2}x_j)}{M_i}\sum_{n=1}^{N_i}\frac{\mu(n+\ell_1)\mu(n+\ell_2)}{n}. \end{align*} $$
Note that
![]() $M_i\approx \log N_i$
. Since the two-term logarithmic Chowla conjecture holds [Reference Tao21], we have
$M_i\approx \log N_i$
. Since the two-term logarithmic Chowla conjecture holds [Reference Tao21], we have
 $$ \begin{align*}\lim_{i\rightarrow \infty} \frac{1}{M_i} \sum_{n=1}^{N_i}\frac{\mu(n+\ell_1)\mu(n+\ell_2)}{n}=0\end{align*} $$
$$ \begin{align*}\lim_{i\rightarrow \infty} \frac{1}{M_i} \sum_{n=1}^{N_i}\frac{\mu(n+\ell_1)\mu(n+\ell_2)}{n}=0\end{align*} $$
for any
![]() $0{\kern-1pt}\le{\kern-1pt} \ell _1{\kern-1pt}\neq{\kern-1pt} \ell _2{\kern-1pt}\le{\kern-1pt} L{\kern-1pt}-{\kern-1pt}1$
. Combining this equality with the fact that
$0{\kern-1pt}\le{\kern-1pt} \ell _1{\kern-1pt}\neq{\kern-1pt} \ell _2{\kern-1pt}\le{\kern-1pt} L{\kern-1pt}-{\kern-1pt}1$
. Combining this equality with the fact that
![]() $\max _{x\in X}|f(x)| \le 1$
, one has that for sufficiently large i,
$\max _{x\in X}|f(x)| \le 1$
, one has that for sufficiently large i,
 $$ \begin{align*} &\bigg|\frac{1}{M_i}\sum_{n=1}^{N_i} \frac{1}{L} \sum_{\ell=0}^{L-1}\frac{ \mu(n+\ell) f(T^\ell x_{j_n}) }{n} \bigg|^2\\ &\quad<\epsilon + \sum_{j=1}^m\frac{1}{L^2}\sum_{\ell=0}^{L-1}\sum_{j=1}^m\frac{|f(T^{\ell}x_j) \overline{f}(T^{\ell}x_j)|}{M_i}\sum_{n=1}^{N_i}\frac{|\mu(n+\ell)\mu(n+\ell)|}{n}\\ &\quad\le \epsilon+\frac{m}{L^2}\sum_{l=0}^{L-1}\frac{1}{M_i}\sum_{n=1}^{N_i}\frac{1}{n}\\ &\quad=\epsilon+\frac{m}{L}\\ &\quad\overset{({\textrm{A}}.5)}< 2\epsilon. \end{align*} $$
$$ \begin{align*} &\bigg|\frac{1}{M_i}\sum_{n=1}^{N_i} \frac{1}{L} \sum_{\ell=0}^{L-1}\frac{ \mu(n+\ell) f(T^\ell x_{j_n}) }{n} \bigg|^2\\ &\quad<\epsilon + \sum_{j=1}^m\frac{1}{L^2}\sum_{\ell=0}^{L-1}\sum_{j=1}^m\frac{|f(T^{\ell}x_j) \overline{f}(T^{\ell}x_j)|}{M_i}\sum_{n=1}^{N_i}\frac{|\mu(n+\ell)\mu(n+\ell)|}{n}\\ &\quad\le \epsilon+\frac{m}{L^2}\sum_{l=0}^{L-1}\frac{1}{M_i}\sum_{n=1}^{N_i}\frac{1}{n}\\ &\quad=\epsilon+\frac{m}{L}\\ &\quad\overset{({\textrm{A}}.5)}< 2\epsilon. \end{align*} $$
This ends the proof of Lemma A.2.
B Appendix. Proof of Theorem 1.4
In this appendix, we prove Theorem 1.4. As in the proof of Theorem 1.3, we let p be the zero of
![]() $\mathbb {C}$
. For a sequence
$\mathbb {C}$
. For a sequence
![]() $y\in (\mathbb {T}\cup \{p\})^{\mathbb {Z}}$
, we put
$y\in (\mathbb {T}\cup \{p\})^{\mathbb {Z}}$
, we put
![]() $X_y=\overline {\{\sigma ^ny:n\in \mathbb {Z}\}}$
, where
$X_y=\overline {\{\sigma ^ny:n\in \mathbb {Z}\}}$
, where
![]() $\sigma $
is the left shift. To this aim, we give a lemma first.
$\sigma $
is the left shift. To this aim, we give a lemma first.
Lemma B.1. If there exist a non-empty compact subset C of
![]() $[0,1]$
and
$[0,1]$
and
![]() $\beta \in \mathbb {R}$
such that
$\beta \in \mathbb {R}$
such that
then there is
![]() $y\in (\mathbb {T}\cup \{p\})^{\mathbb {Z}}$
such that
$y\in (\mathbb {T}\cup \{p\})^{\mathbb {Z}}$
such that
![]() $(y,C)$
meets Property
$(y,C)$
meets Property
![]() $(*)$
in Lemma 3.4 and
$(*)$
in Lemma 3.4 and
where
![]() $\widetilde F: X_y\to \mathbb {C}$
is a continuous function defined by
$\widetilde F: X_y\to \mathbb {C}$
is a continuous function defined by
![]() $\widetilde F( z)=z(0)$
if
$\widetilde F( z)=z(0)$
if
![]() $z(0)\in \mathbb {T}$
and
$z(0)\in \mathbb {T}$
and
![]() $0$
if
$0$
if
![]() $z(0)=p$
.
$z(0)=p$
.
Proof. It follows by a similar arguments of the proof of Lemma 3.4.
Now we are going to prove Theorem 1.4.
Proof of Theorem 1.4
Assume the contrary that Theorem 1.4 does not hold. Then there exists a non-empty compact subset C of
![]() $[0,1]$
such that
$[0,1]$
such that
![]() $\mathrm{Dim}_P C=0$
and
$\mathrm{Dim}_P C=0$
and
Thus, there is
![]() $\beta \in \{0,\tfrac 14,\tfrac 24,\tfrac 34\}$
with
$\beta \in \{0,\tfrac 14,\tfrac 24,\tfrac 34\}$
with
By Lemma B.1, there is
![]() $y\in (\mathbb {T}\cup \{p\})^{\mathbb {Z}}$
such that
$y\in (\mathbb {T}\cup \{p\})^{\mathbb {Z}}$
such that
![]() $(y,C)$
meets Property
$(y,C)$
meets Property
![]() $(*)$
in Lemma 3.4 and
$(*)$
in Lemma 3.4 and
where
![]() $\widetilde F: X_y\to \mathbb {R}$
is a continuous function defined by
$\widetilde F: X_y\to \mathbb {R}$
is a continuous function defined by
![]() $\widetilde F( z)=z(0)$
if
$\widetilde F( z)=z(0)$
if
![]() $z(0)\in \mathbb {T}$
and
$z(0)\in \mathbb {T}$
and
![]() $0$
if
$0$
if
![]() $z(0)=p$
. By Lemma 3.5, the t.d.s.
$z(0)=p$
. By Lemma 3.5, the t.d.s.
![]() $(X_y,\sigma )$
satisfies
$(X_y,\sigma )$
satisfies
since
![]() $\mathrm{Dim}_P C=0$
. Using the result of [Reference Huang, Wang and Ye11], one has
$\mathrm{Dim}_P C=0$
. Using the result of [Reference Huang, Wang and Ye11], one has
This conflicts with equation (B.3) and the theorem follows. This ends the proof of Theorem 1.4.