Article contents
Pointwise ergodic theorems beyond amenable groups
Published online by Cambridge University Press: 16 April 2012
Abstract
We prove pointwise and maximal ergodic theorems for probability-measure-preserving (PMP) actions of any countable group, provided it admits an essentially free, weakly mixing amenable action of stable type III $_1$. We show that this class contains all irreducible lattices in connected semi-simple Lie groups without compact factors. We also establish similar results when the stable type is III
$_1$. We show that this class contains all irreducible lattices in connected semi-simple Lie groups without compact factors. We also establish similar results when the stable type is III $_\lambda $,
$_\lambda $, 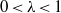 $0 \lt \lambda \lt 1$, under a suitable hypothesis. Our approach is based on the following two principles. First, we show that it is possible to generalize the ergodic theory of PMP actions of amenable groups to include PMP amenable equivalence relations. Secondly, we show that it is possible to reduce the proof of ergodic theorems for PMP actions of a general group to the proof of ergodic theorems in an associated PMP amenable equivalence relation, provided the group admits an amenable action with the properties stated above.
$0 \lt \lambda \lt 1$, under a suitable hypothesis. Our approach is based on the following two principles. First, we show that it is possible to generalize the ergodic theory of PMP actions of amenable groups to include PMP amenable equivalence relations. Secondly, we show that it is possible to reduce the proof of ergodic theorems for PMP actions of a general group to the proof of ergodic theorems in an associated PMP amenable equivalence relation, provided the group admits an amenable action with the properties stated above.
- Type
- Research Article
- Information
- Copyright
- Copyright © 2012 Cambridge University Press
References
- 12
- Cited by




