Hostname: page-component-77c89778f8-9q27g Total loading time: 0 Render date: 2024-07-16T10:50:34.890Z Has data issue: false hasContentIssue false
  • English
  • Français

Point transitivity, 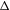${\rm\Delta}$-transitivity and multi-minimality

Published online by Cambridge University Press:  14 March 2014

ZHIJING CHEN ,
JIAN LI  and
JIE LÜ
ZHIJING CHEN
Affiliation:
Department of Mathematics, Sun Yat-Sen University, Guangzhou 510275, PR China email chzhjing@mail2.sysu.edu.cn
JIAN LI
Affiliation:
Department of Mathematics, Shantou University, Shantou, Guangdong 515063, PR China email lijian09@mail.ustc.edu.cn
JIE LÜ
Affiliation:
School of Mathematics, South China Normal University, Guangzhou 510631, PR China email ljie@scnu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

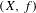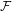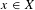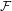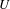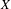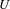Let $(X,f)$ be a topological dynamical system and ${\mathcal{F}}$ be a Furstenberg family (a collection of subsets of $\mathbb{N}$ with hereditary upward property). A point $x\in X$ is called an ${\mathcal{F}}$-transitive point if for every non-empty open subset $U$ of $X$ the entering time set of $x$ into $U$, 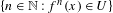$\{n\in \mathbb{N}:f^{n}(x)\in U\}$, is in 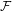${\mathcal{F}}$; the system $(X,f)$ is called 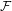${\mathcal{F}}$-point transitive if there exists some 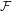${\mathcal{F}}$-transitive point. In this paper, we first discuss the connection between 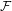${\mathcal{F}}$-point transitivity and 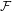${\mathcal{F}}$-transitivity, and show that weakly mixing and strongly mixing systems can be characterized by 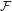${\mathcal{F}}$-point transitivity, completing results in [Transitive points via Furstenberg family. Topology Appl. 158 (2011), 2221–2231]. We also show that multi-transitivity, 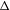${\rm\Delta}$-transitivity and multi-minimality can be characterized by 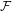${\mathcal{F}}$-point transitivity, answering two questions proposed by Kwietniak and Oprocha [On weak mixing, minimality and weak disjointness of all iterates. Ergod. Th. & Dynam. Sys. 32 (2012), 1661–1672].

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 5 , August 2015 , pp. 1423 - 1442
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akin, E.. Recurrence in Topological Dynamical Systems: Families and Ellis Actions (The University Series in Mathematics). Plenum Press, New York, 1997.CrossRefGoogle Scholar
Banks, J., Nguyen, T. T. D., Oprocha, P. and Trotta, B.. Dynamics of Spacing Shifts. Discrete Contin. Dyn. Syst. 33(9) (2013), 4207–4232.CrossRefGoogle Scholar
Bayart, F. and Grivaux, S.. Frequently hypercyclic operators. Trans. Amer. Math. Soc. 358 (2006), 5083–5117.CrossRefGoogle Scholar
Bayart, F. and Matheron, É.. (Non-)weakly mixing operators and hypercyclicity sets. Ann. Inst. Fourier (Grenoble) 59 (2009), 1–35.CrossRefGoogle Scholar
Chen, J., Li, J. and Lü, J.. On multi-transitivity with respect to a vector. Sci. China Math. to appear; Preprint arXiv:1307.3817.Google Scholar
Furstenberg, H.. Disjointness in ergodic theory, minimal sets, and a problem in diophantine approximation. Math. Systems Theory 1 (1967), 1–49.CrossRefGoogle Scholar
Furstenberg, H.. Recurrence in Ergodic Theory and Combinatorial Number Theory (M. B. Porter Lectures). Princeton University Press, Princeton, NJ, 1981.CrossRefGoogle Scholar
Furstenberg, H. and Weiss, B.. Topological dynamics and combinatorial number theory. J. Anal. Math. 34 (1978), 61–85.CrossRefGoogle Scholar
Glasner, E.. Topological ergodic decompositions and applications to products of powers of a minimal transformation. J. Anal. Math. 64 (1994), 241–262.CrossRefGoogle Scholar
Glasner, E.. Structure Theory as a Tool in Topological Dynamics (London Mathematical Society Lecture Note Series, 277). 2000, pp. 173–209.Google Scholar
Glasner, E.. Ergodic Theory via Joinings (Mathematical Surveys and Monographs, 101). American Mathematical Society, Providence, RI, 2003.CrossRefGoogle Scholar
Glasner, E.. Classifying dynamical systems by their recurrence properties. Topol. Methods Nonlinear Anal. 24 (2004), 21–40.CrossRefGoogle Scholar
Gottschalk, W. H. and Hedlund, G. A.. Topological Dynamics (Collooquium Publications, 36). American Mathematical Society, Providence, RI, 1955.CrossRefGoogle Scholar
Grosse-Erdmann, K.-G. and Peris, A.. Frequently dense orbits. C. R. Math. Acad. Sci. Paris 341 (2005), 123–128.CrossRefGoogle Scholar
Grosse-Erdmann, K. G. and Peris, A.. Weakly mixing operators on topological vector spaces. RACSAM Rev. R. Acad. Cienc. Exactas Fis. Nat. Ser. A Mat. 104 (2010), 413–426.CrossRefGoogle Scholar
Grosse-Erdmann, K. G. and Peris, A.. Linear Chaos (Universitext). Springer, London, 2011.CrossRefGoogle Scholar
He, W. and Zhou, Z.. A topologically mixing system with its measure center being a singleton. Acta Math. Sinica 45(5) (2002), 929–934.Google Scholar
Huang, W., Park, K. K. and Ye, X.. Dynamical systems disjoint from all minimal systems with zero entropy. Bull. Soc. Math. France 135 (2007), 259–282.CrossRefGoogle Scholar
Huang, W. and Ye, X.. Topological complexity, return times and weak disjointness. Ergod. Th. & Dyn. Sys. 24 (2004), 825–846.CrossRefGoogle Scholar
Huang, W. and Ye, X.. Dynamical systems disjoint from any minimal system. Trans. Amer. Math. Soc. 357(2) (2005), 669–694.CrossRefGoogle Scholar
Kwietniak, D. and Oprocha, P.. On weak mixing, minimality and weak disjointness of all iterates. Ergod. Th. & Dynam. Sys. 32 (2012), 1661–1672.CrossRefGoogle Scholar
Keynes, H. and Newton, D.. Real prime flows. Trans. Amer. Math. Soc. 217 (1976), 237–255.CrossRefGoogle Scholar
Lau, K. and Zame, A.. On weak mixing of cascades. Math. Systems Theory 6 (1973), 307–311.CrossRefGoogle Scholar
Li, J.. Transitive points via Furstenberg family. Topology Appl. 158 (2011), 2221–2231.CrossRefGoogle Scholar
Moothathu, T. K. S.. Weak mixing and mixing of a single transformation of a topological (semi)group. Aequationes Math. 78 (2009), 147–155.CrossRefGoogle Scholar
Moothathu, T. K. S.. Diagonal points having dense orbit. Colloq. Math. 120 (2010), 127–138.CrossRefGoogle Scholar
Oprocha, P. and Zhang, G. H.. On local aspects of topological weak mixing in dimension one and beyond. Studia Math. 202 (2011), 261–288.CrossRefGoogle Scholar
Peris, A.. Topologically Ergodic Operators (Function Theory on Infinite Dimensional Spaces IX, Madrid, 2005), http://www.mat.ucm.es/∼confexx/web\_confe\_05/index.htm.Google Scholar