Article contents
Marked boundary rigidity for surfaces
Published online by Cambridge University Press: 08 November 2016
Abstract
We show that, on an oriented compact surface, two sufficiently 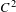 $C^{2}$-close Riemannian metrics with strictly convex boundary, no conjugate points, hyperbolic trapped set for their geodesic flows and the same marked boundary distance are isometric via a diffeomorphism that fixes the boundary. We also prove that the same conclusion holds on a compact surface for any two negatively curved Riemannian metrics with strictly convex boundary and the same marked boundary distance, extending a result of Croke and Otal.
$C^{2}$-close Riemannian metrics with strictly convex boundary, no conjugate points, hyperbolic trapped set for their geodesic flows and the same marked boundary distance are isometric via a diffeomorphism that fixes the boundary. We also prove that the same conclusion holds on a compact surface for any two negatively curved Riemannian metrics with strictly convex boundary and the same marked boundary distance, extending a result of Croke and Otal.
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2016
References
- 5
- Cited by




