Hostname: page-component-7479d7b7d-q6k6v Total loading time: 0 Render date: 2024-07-12T20:06:50.519Z Has data issue: false hasContentIssue false
  • English
  • Français

Hyperbolicity in the volume-preserving scenario

Published online by Cambridge University Press:  23 August 2012

ALEXANDER ARBIETO  and
THIAGO CATALAN
ALEXANDER ARBIETO
Affiliation:
Instituto de Matemática, Universidade Federal do Rio de Janeiro, PO Box 68530, 21945-970 Rio de Janeiro, Brazil (email: arbieto@im.ufrj.br)
THIAGO CATALAN
Affiliation:
Faculdade de Matemática, Universidade Federal de Uberlândia, 34-32309442 Uberlândia-MG, Brazil (email: tcatalan@famat.ufu.br)
Get access Rights & Permissions [Opens in a new window]

Abstract

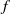Extending a result of Mañé, Hayashi proved that every diffeomorphism $f$ which has a 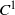$C^1$-neighborhood 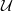$\mathcal {U}$ where all periodic points of any 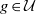$g\in \mathcal {U}$are hyperbolic is an Axiom A diffeomorphism. Here we prove the analogous result in the volume-preserving scenario.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 33 , Issue 6 , December 2013 , pp. 1644 - 1666
Copyright
Copyright © 2012 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Abdenur, F.. Generic robustness of spectral decompositions. Ann. Sci. Éc. Norm. Supér. (4) 36(2) (2003), 213–224.Google Scholar
[2]Abdenur, F., Bonatti, C., Crovisier, S., Diaz, L. and Wen, L.. Periodic points and homoclinic classes. Ergod. Th. & Dynam. Sys. 27 (2007), 1–22.CrossRefGoogle Scholar
[3]Araújo, V. and Pacífico, M. J.. Three-dimensional Flows (Results in Mathematics and Related Areas. 3rd Series, 53). Springer, Heidelberg, 2010.Google Scholar
[4]Arbieto, A. and Matheus, C.. A pasting lemma and some applications for conservative systems. Ergod. Th. Dynam. Sys. 27(5) (2007), 1399–1417.Google Scholar
[5]Arbieto, A., Senos, L. and Sodero, T.. The specification property for flows from the robust and generic viewpoint. Preprint, 2011, arXiv:1101.3445. J. Differential Equations to appear.CrossRefGoogle Scholar
[6]Arnaud, M.-C.. Le ‘Closing lemma’ en topologie $C^1$ (Mémoires de la Société Mathématique de France, 74). Société Mathématique de France, Paris, 1998.Google Scholar
[7]Avila, A.. On the regularization of conservative maps. Acta Math. 205(1) (2010), 5–18.Google Scholar
[8]Avila, A., Bochi, J. and Wilkinson, A.. Nonuniform center bunching and the genericity of ergodicity among $C^1$ partially hyperbolic symplectomorphisms. Ann. Sci. Éc. Norm. Supér. (4) 42(6) (2009), 931–979.Google Scholar
[9]Bessa, M.. Generic incompressible flows are topological mixing. C. R. Math. Acad. Sci. Paris 346 (2008), 1169–1174.Google Scholar
[10]Bessa, M. and Rocha, J.. On $C^1$-robust transitivity of volume-preserving flows. J. Differential Equations 245(11) (2008), 3127–3143.Google Scholar
[11]Bessa, M. and Rocha, J.. Three-dimensional conservative star flows are Anosov. Discrete Contin. Dyn. Syst. A 26 (2010), 839–846.Google Scholar
[12]Bessa, M., Ferreira, C. and Rocha, J.. On the stability of the set of hyperbolic closed orbits of a Hamiltonian. Math. Proc. Cambridge Philos. Soc. 149(2) (2010), 373–383.Google Scholar
[13]Bochi, J.. $C^1$-generic symplectic diffeomorphisms: partial hyperbolicity and zero centre Lyapunov exponents. J. Inst. Math. Jussieu 9(1) (2010), 49–93.Google Scholar
[14]Bonatti, C. and Crovisier, S.. Récurrence et générecité. Invent. Math. 158 (2004), 33–104.Google Scholar
[15]Bonatti, C., Diaz, L. and Pujals, H.. A $C^1$-generic dichotomy for diffeomorphisms: weak forms of hyperbolicity or infinitely many sinks or sources. Ann. of Math. (2) 158 (2003), 355–418.CrossRefGoogle Scholar
[16]Carballo, C., Moralles, C. and Pacifico, M.. Homoclinic classes for generic $C^1$ vector fields. Ergod. Th. & Dynam. Sys. 23 (2003), 403–415.CrossRefGoogle Scholar
[17]Crovisier, S.. Perturbation de la dynamique de diffeomorphismes en topologie $C^1$. Preprint, 2009, arXiv:0912.2896.Google Scholar
[18]Crovisier, S.. Birth of homoclinic intersections: a model for the central dynamics of partially hyperbolic systems. Ann. of Math. (2) 172(3) (2010), 1641–1677.Google Scholar
[19]Ferreira, C.. Stability properties of divergence-free vector fields, Preprint, 2010, arXiv:1004.2893.Google Scholar
[20]Franks, J.. Necessary conditions for stability of diffeomorphisms. Trans. Amer. Math. Soc. 158 (1971), 301–308.Google Scholar
[21]Gan, S.. Another proof for $C^1$ stability conjecture for flows. Sci. China Ser. A 41(10) (1998), 1076–1082.Google Scholar
[22]Gan, S. and Wen, L.. Nonsingular star flows satisfy Axiom A and the no-cycle condition. Invent. Math. 164(2) (2006), 279–315.Google Scholar
[23]Hayashi, S.. Diffeomorphisms in $\mathcal {F}^1(M)$ satisfy Axiom A. Ergod. Th. & Dynam. Sys. 12 (1992), 233–253.CrossRefGoogle Scholar
[24]Hayashi, S.. Connecting invariant manifolds and the solution of the $C^1$ stability and $\Omega $-stability conjectures for flows. Ann. of Math. (2) 145(1) (1997), 81–137.Google Scholar
[25]Horita, V. and Tahzibi, A.. Partial hyperbolicity for symplectic diffeomorphisms. Ann. Inst. H. Poincaré Anal. Non Linéaire 23(5) (2006), 641–661.Google Scholar
[26]Li, M., Gan, S. and Wen, L.. Robustly transitive singular sets via approach of an extended linear Poincaré flow. Discrete Contin. Dyn. Syst. 13(2) (2005), 239–269.Google Scholar
[27]Liang, C., Liu, G. and Sun, W.. Equivalent conditions of dominated splittings for volume-preserving diffeomorphism. Acta Math. Sinica 23 (2007), 1563–1576.CrossRefGoogle Scholar
[28]Liao, S. T.. A basic property of a certain class of differential systems. Acta Math. Sinica 22 (1979), 316–343 (in Chinese).Google Scholar
[29]Mañé, R.. An ergodic closing lemma. Ann. of Math. (2) 116(3) (1982), 503–540.Google Scholar
[30]Mañé, R.. A proof of the $C^1$ stability conjecture. Publ. Math. Inst. Hautes Études Sci. 66 (1987), 161–210.Google Scholar
[31]Newhouse, S. E.. Quasi-elliptic periodic points in conservative dynamical systems. Amer. J. Math. 99(5) (1977), 1061–1087.CrossRefGoogle Scholar
[32]Palis, J.. Global perspective for non-conservative dynamics. Ann. Inst. H. Poincaré Anal. Non Linéaire 22 (2005), 485–507.Google Scholar
[33]Palis, J.. On the $C^1$$\Omega $-stability conjecture. Publ. Math. Inst. Hautes Études Sci. 66 (1988), 211–215.Google Scholar
[34]Pugh, C. and Robinson, C.. The $C^1$ closing lemma, including Hamiltonians. Ergod. Th. & Dynam. Sys. 3(2) (1983), 261–313.CrossRefGoogle Scholar
[35]Pujals, E. and Sambarino, M.. Homoclinic tangencies and hyperbolicity for surface diffeomorphisms. Ann. of Math. (2) 151 (2000), 961–1023.Google Scholar
[36]Robinson, C.. Generic properties of conservative systems. Amer. J. Math. 92 (1970), 562–603.Google Scholar
[37]Toyoshiba, H.. Vector fields in the interior of Kupka–Smale systems satisfy Axiom A. J. Differential Equations 177(1) (2001), 27–48.Google Scholar
[38]Vivier, T.. Projective hyperbolicity and fixed points. Ergod. Th. & Dynam. Sys. 26 (2006), 923–936.CrossRefGoogle Scholar
[39]Xia, Z.. Homoclinic points in symplectic and volume-preserving diffeomorphisms. Commun. Math. Phys. 177 (1996), 435–449.Google Scholar
[40]Xia, Z. and Wen, L.. $C^1$ connecting lemmas. Trans. Amer. Math. Soc. 352(11) (2000), 5213–5230.Google Scholar
[41]Zuppa, C.. Régularisation $C^{\infty }$ des champs vectoriels qui préservent l’élément de volume. Bol. Soc. Brasil. Mat. 10(2) (1979), 51–56.Google Scholar