Hostname: page-component-7479d7b7d-pfhbr Total loading time: 0 Render date: 2024-07-12T19:49:36.560Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamical systems of type 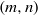$(m,n)$ and their 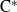$\mathrm {C}^*$-algebras

Published online by Cambridge University Press:  27 July 2012

PERE ARA ,
RUY EXEL  and
TAKESHI KATSURA
PERE ARA
Affiliation:
Departament de Matemátiques, Universitat Autònoma de Barcelona, 08193 Bellaterra (Barcelona), Spain (email: para@mat.uab.cat)
RUY EXEL
Affiliation:
Departamento de Matemática, Universidade Federal de Santa Catarina, 88010-970 Florianópolis SC, Brazil (email: exel@mtm.ufsc.br)
TAKESHI KATSURA
Affiliation:
Department of Mathematics, Faculty of Science and Technology, Keio University, 3-14-1 Hiyoshi, Kouhoku-ku, Yokohama, 223-8522, Japan (email: katsura@math.keio.ac.jp)
Get access Rights & Permissions [Opens in a new window]

Abstract

Given positive integers $n$ and 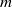$m$, we consider dynamical systems in which (the disjoint union of) $n$ copies of a topological space is homeomorphic to 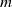$m$ copies of that same space. The universal such system is shown to arise naturally from the study of a C*-algebra denoted by 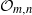${\cal O}_{m,n}$, which in turn is obtained as a quotient of the well-known Leavitt C*-algebra $L_{m,n}$, a process meant to transform the generating set of partial isometries of 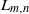$L_{m,n}$ into a tame set. Describing 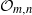${\cal O}_{m,n}$ as the crossed product of the universal 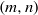$(m,n)$-dynamical system by a partial action of the free group 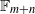$\mathbb {F}_{m+n}$, we show that 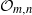${\cal O}_{m,n}$ is not exact when $n$ and 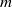$m$ are both greater than or equal to 2, but the corresponding reduced crossed product, denoted by 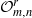${\cal O}_{m,n}^r$, is shown to be exact and non-nuclear. Still under the assumption that 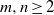$m,n\geq 2$, we prove that the partial action of 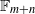$\mathbb {F}_{m+n}$ is topologically free and that 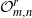${\cal O}_{m,n}^r$ satisfies property (SP) (small projections). We also show that 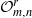${\cal O}_{m,n}^r$admits no finite-dimensional representations. The techniques developed to treat this system include several new results pertaining to the theory of Fell bundles over discrete groups.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 33 , Issue 5 , October 2013 , pp. 1291 - 1325
Copyright
Copyright © 2012 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[AA]Abrams, G. and Aranda Pino, G.. The Leavitt path algebra of a graph. J. Algebra 293 (2005), 319–334.Google Scholar
[AG1]Ara, P. and Goodearl, K. R.. Leavitt path algebras of separated graphs J. Reine Angew. Math. doi:10.1515/CRELLE.2011.146 [arXiv:1004.4979v2 math.RA].Google Scholar
[AG2]Ara, P. and Goodearl, K. R.. C*-algebras of separated graphs. J. Funct. Anal. 261 (2011), 2540–2568.Google Scholar
[AMP]Ara, P., Moreno, M. A. and Pardo, E.. Nonstable $K$-theory for graph algebras. Algebr. Represent. Theory 10 (2007), 157–178.CrossRefGoogle Scholar
[B]Brown, L. G.. Ext of certain free product C*-algebras. J. Operator Theory 6 (1981), 135–141.Google Scholar
[BO]Brown, N. P. and Ozawa, N.. C*-Algebras and Finite-dimensional Approximations (Graduate Studies in Mathematics, 88). American Mathematical Society, Providence, RI, 2008.Google Scholar
[C]Cohen, D. E.. Combinatorial Group Theory: A Topological Approach (London Mathematical Society Student Texts, 14). Cambridge University Press, Cambridge, 1989.Google Scholar
[CK]Cuntz, J. and Krieger, W.. A class of C*-algebras and topological Markov chains. Invent. Math. 56 (1980), 251–268.CrossRefGoogle Scholar
[DP]Duncan, J. and Paterson, A. L. T.. C*-algebras of inverse semigroups. Proc. Edinb. Math. Soc. (2) 28(1) (1985), 41–58.Google Scholar
[E1]Exel, R.. Circle actions on C*-algebras, partial automorphisms and a generalized Pimsner–Voiculescu exact sequence. J. Funct. Anal. 122 (1994), 361–401.CrossRefGoogle Scholar
[E2]Exel, R.. Amenability for Fell bundles. J. Reine Angew. Math. 492 (1997), 41–73.Google Scholar
[E3]Exel, R.. Partial representations and amenable Fell bundles over free groups. Pacific J. Math. 192 (2000), 39–63.Google Scholar
[E4]Exel, R.. Exact groups, induced ideals, and Fell bundles. Preprint, 2003; arXiv:math.OA/0012091 (this paper was published as ‘Exact groups and Fell bundles’, Math. Ann. 323 (2002), (2), 259–266. However, the referee required that the results pertaining to induced ideals be removed from the preprint version arguing that there were no applications of this concept. The reader will therefore have to consult the arxiv version, where the results we need may be found).Google Scholar
[E5]Exel, R.. Twisted partial actions: a classification of regular $\mathrm {C}^*$-algebraic bundles. Proc. Lond. Math. Soc. (3) 74 (1997), 417–443.Google Scholar
[EL]Exel, R. and Laca, M.. Cuntz–Krieger algebras for infinite matrices. J. Reine Angew. Math. 512 (1999), 119–172.Google Scholar
[ELQ]Exel, R., Laca, M. and Quigg, J.. Partial dynamical systems and C*-algebras generated by partial isometries. J. Operator Theory 47(1) (2002), 169–186; arXiv:funct-an/9712007v1.Google Scholar
[FD]Fell, J. M. G. and Doran, R. S.. Representations of *-algebras, Locally Compact Groups, and Banach *-algebraic Bundles. Vols. 1 & 2 (Pure and Applied Mathematics, 126). Academic Press, 1988.Google Scholar
[H]Hazrat, R.. The graded structure of Leavitt path algebras. Israel J. Math. to appear [arXiv:1005.1900v6  math.RA].Google Scholar
[KR]Kirchberg, E. and Rørdam, M.. Infinite non-simple $C^*$-algebras: Absorving the Cuntz algebra ${\cal O}_{\infty }$. Adv. Math. 167 (2002), 195–264.Google Scholar
[L]Leavitt, W. G.. The module type of a ring. Trans. Amer. Math. Soc. 103 (1962), 113–130.Google Scholar
[M1]McClanahan, K.. C*-algebras generated by elements of a unitary matrix. J. Funct. Anal. 107 (1992), 439–457.Google Scholar
[M2]McClanahan, K.. K-theory and Ext-theory for rectangular unitary C*-algebras. Rocky Mountain J. Math. 23 (1993), 1063–1080.Google Scholar
[M3]McClanahan, K.. Simplicity of reduced amalgamated products of C*-algebras. Canad. J. Math. 46 (1994), 793–807.Google Scholar
[M4]McClanahan, K.. $K$-theory for partial crossed products by discrete groups. J. Funct. Anal. 130 (1995), 77–117.Google Scholar