Hostname: page-component-84b7d79bbc-lrf7s Total loading time: 0 Render date: 2024-07-25T15:19:32.524Z Has data issue: false hasContentIssue false
  • English
  • Français

The 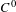$C^{0}$ integrability of symplectic twist maps without conjugate points

Part of: Finite-dimensional Hamiltonian, Lagrangian, contact, and nonholonomic systems Smooth dynamical systems: general theory Low-dimensional dynamical systems

Published online by Cambridge University Press:  15 August 2019

MARC ARCOSTANZO
MARC ARCOSTANZO*
Affiliation:
Laboratoire de Mathématiques d’Avignon (EA2151), Avignon Université, France email marc.arcostanzo@univ-avignon.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

It is proved that a symplectic twist map of the cotangent bundle 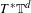$T^{\ast }\mathbb{T}^{d}$ of the 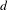$d$-dimensional torus that is without conjugate points is 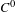$C^{0}$-integrable, that is  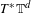$T^{\ast }\mathbb{T}^{d}$ is foliated by a family of invariant 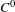$C^{0}$ Lagrangian graphs.

Keywords

symplectic twist mapcomplete integrabilityweak KAM theory

MSC classification

Primary: 37C25: Fixed points, periodic points, fixed-point index theory 37E40: Twist maps 37J35: Completely integrable systems, topological structure of phase space, integration methods
Secondary: 37J45: Periodic, homoclinic and heteroclinic orbits; variational methods, degree-theoretic methods
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 1 , January 2021 , pp. 48 - 65
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arcostanzo, M., Arnaud, M.-C., Bolle, P. and Zavidovique, M.. Tonelli Hamiltonians without conjugate points and C 0 -integrability. Math. Z. 280 (2015), 165–194.Google Scholar
Arnaud, M.-C.. Lower and upper bounds for the Lyapunov exponents of twisting dynamics: a relationship between the exponents and the angle of Oseledets’ splitting. Ergod. Th. & Dynam. Sys. 33 (2013), 693–712.Google Scholar
Bialy, M.. Rigidity for convex billiards on the hemisphere and hyperbolic plane. DCDS 33 (2013), 3903–3913.Google Scholar
Bialy, M. L. and MacKay, R. S.. Symplectic twist maps without conjugate points. Israel J. Math. 141 (2004), 235–247.Google Scholar
Busemann, H.. The Geometry of Geodesics. Academic Press, London, 1955.Google Scholar
Cheng, J. and Sun, Y.. A necessary and sufficient condition for a twist map being integrable. Sci. China (Ser. A) 39 (1996), 709–717.Google Scholar
Dold, A.. Lectures on Algebraic Topology. Springer, Berlin, 1972.Google Scholar
Garibaldi, E. and Thieullen, P.. Minimizing orbits in the discrete Aubry-Mather model. Nonlinearity 24 (2011), 563–611.Google Scholar
Gole, C.. Symplectic Twist Maps. World Scientific, Singapore, 2001.Google Scholar
Heber, J.. On the geodesic flow of tori without conjugate points. Math. Z. 216 (1994), 209–216.Google Scholar
Mackay, R. S., Meiss, J. D. and Stark, J.. Converse KAM theory for symplectic twist maps. Nonlinearity 2 (1989), 555–570.Google Scholar
Struwe, M.. Variational Methods—Applications to Nonlinear Partial Differential Equations and Hamiltonian Systems, 4th edn. Springer, Berlin, 2008.Google Scholar