Article contents
Asymptotic spectral gap and Weyl law for Ruelle resonances of open partially expanding maps
Published online by Cambridge University Press: 07 October 2015
Abstract
We consider a simple model of an open partially expanding map. Its trapped set 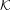 ${\mathcal{K}}$ in phase space is a fractal set. We first show that there is a well-defined discrete spectrum of Ruelle resonances which describes the asymptotic of correlation functions for large time and which is parametrized by the Fourier component
${\mathcal{K}}$ in phase space is a fractal set. We first show that there is a well-defined discrete spectrum of Ruelle resonances which describes the asymptotic of correlation functions for large time and which is parametrized by the Fourier component  $\unicode[STIX]{x1D708}$ in the neutral direction of the dynamics. We introduce a specific hypothesis on the dynamics that we call ‘minimal captivity’. This hypothesis is stable under perturbations and means that the dynamics is univalued in a neighborhood of
$\unicode[STIX]{x1D708}$ in the neutral direction of the dynamics. We introduce a specific hypothesis on the dynamics that we call ‘minimal captivity’. This hypothesis is stable under perturbations and means that the dynamics is univalued in a neighborhood of 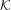 ${\mathcal{K}}$. Under this hypothesis we show the existence of an asymptotic spectral gap and a fractal Weyl law for the upper bound of density of Ruelle resonances in the semiclassical limit
${\mathcal{K}}$. Under this hypothesis we show the existence of an asymptotic spectral gap and a fractal Weyl law for the upper bound of density of Ruelle resonances in the semiclassical limit 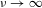 $\unicode[STIX]{x1D708}\rightarrow \infty$. Some numerical computations with the truncated Gauss map and Bowen–Series maps illustrate these results.
$\unicode[STIX]{x1D708}\rightarrow \infty$. Some numerical computations with the truncated Gauss map and Bowen–Series maps illustrate these results.
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2015
References
- 3
- Cited by




