Hostname: page-component-7479d7b7d-c9gpj Total loading time: 0 Render date: 2024-07-12T10:09:44.884Z Has data issue: false hasContentIssue false
  • English
  • Français

OPTIMAL BANDWIDTH CHOICE FOR ESTIMATION OF INVERSE CONDITIONAL–DENSITY–WEIGHTED EXPECTATIONS

Published online by Cambridge University Press:  19 June 2009

David Tomás Jacho-Chávez
David Tomás Jacho-Chávez*
Affiliation:
Indiana University
*
*Address correspondence to David T. Jacho-Chávez, Department of Economics, Indiana University, Wylie Hall 251, 100 South Woodlawn Avenue, Bloomington, IN 47405–7104, USA; e-mail: djachoch@indiana.edu.
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper characterizes the bandwidth value (h) that is optimal for estimating parameters of the form 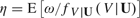, where the conditional density of a scalar continuous random variable V, given a random vector U, 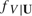, is replaced by its kernel estimator. That is, the parameter η is the expectation of ω inversely weighted by 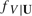, and it is the building block of various semiparametric estimators already proposed in the literature such as Lewbel (1998), Lewbel (2000b), Honoré and Lewbel (2002), Khan and Lewbel (2007), and Lewbel (2007). The optimal bandwidth is derived by minimizing the leading terms of a second-order mean squared error expansion of an in-probability approximation of the resulting estimator with respect to h. The expansion also demonstrates that the bandwidth can be chosen on the basis of bias alone, and that a simple “plug-in” estimator for the optimal bandwidth can be constructed. Finally, the small sample performance of our proposed estimator of the optimal bandwidth is assessed by a Monte Carlo experiment.

Type
ARTICLES
Information
Econometric Theory , Volume 26 , Issue 1 , February 2010 , pp. 94 - 118
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bashtannyk, D.M. & Hyndman, R.J. (2001) Bandwidth selection for kernel conditional density estimation. Computational Statistics & Data Analysis 36, 279–298.CrossRefGoogle Scholar
Chen, X., Linton, O.B., & Robinson, P.M. (2001) The estimation of conditional densities. In Puri, M.L. (ed.) Asymptotics in Statistics and Probability: Papers in Honor of George Gregory Roussas, 1st ed. pp. 71–84. VSP International Science.Google Scholar
Collomb, G. & Härdle, W. (1986) Strong uniform convergence rates in robust nonparametric time series analysis and prediction: Kernel regression estimation from dependent observations. Stochastic Processes and their Application 23(1), 77–89.CrossRefGoogle Scholar
Fernandes, M. & Monteiro, P.K. (2005) Central limit theorem for asymmetric kernel functionals. Annals of the Institute of Statistical Mathematics 57(3), 425–442.CrossRefGoogle Scholar
Gasser, T., Müller, H.-G., & Mammitzsch, V. (1985) Kernels for nonparametric curve estimation. Journal of the Royal Statistical Society. Series B (Methodological) 47, 238–252.CrossRefGoogle Scholar
Goldstein, L. & Messer, K. (1992) Optimal plug-in estimators for nonparametric functional estimation. Annals of Statistics 20(3), 1306–1328.CrossRefGoogle Scholar
Hall, P. & Marron, J.S. (1987) Estimation of integrated squared density derivatives. Statistics and Probability Letters 6(2), 109–115.CrossRefGoogle Scholar
Hall, P., Racine, J.S., & Li, Q. (2004) Cross-validation and the estimation of conditional probability densities. Journal of the American Statistical Association 99(486), 1015–1026.CrossRefGoogle Scholar
Härdle, W., Hart, J.D., Marron, J.S., & Tsybakov, A.B. (1992) Bandwidth choice for average derivative estimation. Journal of the American Statistical Association 87(417), 218–226.Google Scholar
Härdle, W. & Stoker, T.M. (1989) Investigating smooth multiple regression by the method of average derivatives. Journal of the American Statistical Association 84, 986–995.Google Scholar
Härdle, W. & Tsybakov, A.B. (1993) How sensitive are average derivatives? Journal of Econometrics 58, 31–48.CrossRefGoogle Scholar
Hirano, K., Imbens, G.W., & Ridder, G. (2003) Efficient estimation of average treatment effects using the estimated propensity Score. Econometrica 71(4), 1161–1189.CrossRefGoogle Scholar
Honoré, B.E. & Lewbel, A. (2002) Semiparametric binary choice panel data models without strictly exogenous regressors. Econometrica 70(5), 2053–2063.CrossRefGoogle Scholar
Hyndman, R.J., Bashtannyk, D.M., & Grunwald, G.K. (1996) Estimating and visualizing conditional densities. Journal of Computational and Graphical Statistics 5(4), 315–336.Google Scholar
Ichimura, H. & Linton, O.B. (2005) Asymptotic expansions for some semiparametric program evaluation estimators. In Andrews, D.W.K. and Stock, J.H. (eds.), Identification and Inference for Econometric Models: Essays in Honor of Thomas Rothenberg, 1st ed., pp. 149–170. Cambridge University Press.CrossRefGoogle Scholar
Jacho-Chávez, D.T. (2006) Identification, Estimation and Efficiency of Nonparametric and Semiparametric Models in Microeconometrics. Ph.D. thesis, London School of Economics and Political Science.Google Scholar
Jones, M.C. & Sheather, S.J. (1991) Using non-stochastic terms to advantage in kernel-based estimation of integrated squared density derivatives. Statistica and Probability Letters 11(6), 511–514.CrossRefGoogle Scholar
Khan, S. & Lewbel, A. (2007) Weighted and two-stage least squares estimation of semiparametric truncated regression models. Econometric Theory 23(2), 309–347.CrossRefGoogle Scholar
Lewbel, A. (1998) Semiparametric latent variable model estimation with endogenous or mismeasured regressors. Econometrica 66(1), 105–121.CrossRefGoogle Scholar
Lewbel, A. (2000a) Asymptotic Trimming for Bounded Density Plug-in Estimators. Unpublished manuscript, Boston College.Google Scholar
Lewbel, A. (2000b) Semiparametric qualitative response model estimation with unknown heteroscedasticity or instrumental variables. Journal of Econometrics 97(1), 145–177.CrossRefGoogle Scholar
Lewbel, A. (2007) Endogenous selection or treatment model estimation. Journal of Econometrics 141(2), 777–806.CrossRefGoogle Scholar
Linton, O.B. (1991) Edgeworth Approximation in Semiparametric Regression Models. Ph.D. thesis, University of California, Berkeley.Google Scholar
Linton, O.B. (1995) Second order approximation in the partially linear regression model. Econometrica, 63(3), 1079–1112.CrossRefGoogle Scholar
Masry, E. (1996) Multivariate local polynomial regression for time series: Uniform strong consistency and rates. Journal of Time Series Analysis 17(6), 571–599.CrossRefGoogle Scholar
Powell, J.L., Stock, J.H., & Stoker, T.M. (1989) Semiparametric estimation of index coefficients. Econometrica 57(6), 1403–1430.CrossRefGoogle Scholar
Powell, J.L. & Stoker, T.M. (1996) Optimal bandwidth choice for density-weighted averages. Journal of Econometrics 75(2), 291–316.CrossRefGoogle Scholar
Robinson, P.M. (1988) Root n-consistent semiparametric regression. Econometrica 56, 931–954.CrossRefGoogle Scholar
Rosenblatt, M. (1969) Conditional probability density and regression estimators. In Krishnaiah, P.R. (ed.). Multivariate Analysis II, pp. 25–31. Academic Press.Google Scholar
Sherman, R.P. (1994) U-processes in the analysis of a generalized semiparametric regression estimator. Econometric Theory 10(2), 372–395.CrossRefGoogle Scholar
Silverman, B.W. (1978) Weak and strong uniform consistency of the kernel estimate of a density function and its derivatives. Annals of Statistics 6(1), 177–184.CrossRefGoogle Scholar
Silverman, B.W. (1986) Density Estimation for Statistics and Data Analysis, 1st ed.Chapman and Hall.Google Scholar
Srinivasan, T.N. (1970) Approximations to finite sample moments of estimators whose exact sampling distributions are unknown. Econometrica 38(3), 533–541.CrossRefGoogle Scholar
Wand, M.P. & Jones, C. (1995) Kernel Smoothing, vol. 60 of Monographs on Statistics and Applied Probability 1st ed. Chapman and Hall.CrossRefGoogle Scholar