Hostname: page-component-848d4c4894-sjtt6 Total loading time: 0 Render date: 2024-06-21T10:25:41.309Z Has data issue: false hasContentIssue false
  • English
  • Français

A MAX-CORRELATION WHITE NOISE TEST FOR WEAKLY DEPENDENT TIME SERIES

Published online by Cambridge University Press:  12 May 2020

Jonathan B. Hill  and
Kaiji Motegi
Jonathan B. Hill*
Affiliation:
University of North Carolina
Kaiji Motegi
Affiliation:
Kobe University
*
Address correspondence to Jonathan B. Hill, Department of Economics, University of North Carolina at Chapel Hill, Chapel Hill, NC. USA; e-mail: jbhill@email.unc.edu; web: https://jbhill.web.unc.edu.
Get access Rights & Permissions [Opens in a new window]

Abstract

This article presents a bootstrapped p-value white noise test based on the maximum correlation, for a time series that may be weakly dependent under the null hypothesis. The time series may be prefiltered residuals. The test statistic is a normalized weighted maximum sample correlation coefficient 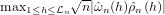$ \max _{1\leq h\leq \mathcal {L}_{n}}\sqrt {n}|\hat {\omega }_{n}(h)\hat {\rho }_{n}(h)|$, where 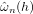$\hat {\omega }_{n}(h)$ are weights and the maximum lag 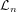$ \mathcal {L}_{n}$ increases at a rate slower than the sample size n. We only require uncorrelatedness under the null hypothesis, along with a moment contraction dependence property that includes mixing and nonmixing sequences. We show Shao’s (2011, Annals of Statistics 35, 1773–1801) dependent wild bootstrap is valid for a much larger class of processes than originally considered. It is also valid for residuals from a general class of parametric models as long as the bootstrap is applied to a first-order expansion of the sample correlation. We prove the bootstrap is asymptotically valid without exploiting extreme value theory (standard in the literature) or recent Gaussian approximation theory. Finally, we extend Escanciano and Lobato’s (2009, Journal of Econometrics 151, 140–149) automatic maximum lag selection to our setting with an unbounded lag set that ensures a consistent white noise test, and find it works extremely well in controlled experiments.

Type
ARTICLES
Information
Econometric Theory , Volume 36 , Issue 5 , October 2020 , pp. 907 - 960
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

We thank three referees, Co-Editor Michael Jansson, and Editor Peter C.B. Phillips for helpful comments and suggestions that led to significant improvements to our manuscript. We also thank Eric Ghysels, Shigeyuki Hamori, Peter R. Hansen, Yoshihiko Nishiyama, Kenichiro Tamaki, Kozo Ueda, and Zheng Zhang, seminar participants at the Kyoto Institute of Economic Research, UNC Chapel Hill, the University of Essex, and Kobe University, and conference participants at the 10th Spring Meeting of JSS, 2016 SWET, 2016 AMES, 2016 JJSM, 2016 NBER-NSF Time Series Conference, the 15th International Conference of WEAI, and SETA 2019 for helpful comments. The second author is grateful for financial support from JSPS KAKENHI (Grant Number 16K17104), Kikawada Foundation, Mitsubishi UFJ Trust Scholarship Foundation, Nomura Foundation, and Suntory Foundation.

References

REFERENCES

Andrews, D.W.K.(1987) Consistency in nonlinear econometric models: A generic uniform law of large numbers. Econometrica 55, 1465–1471.CrossRefGoogle Scholar
Andrews, D.W.K. (1991) Heteroskedasticity and autocorrelation consistent covariance matrix estimation. Econometrica 59, 817–858.CrossRefGoogle Scholar
Andrews, D.W.K. &W., Ploberger (1996) Testing for serial correlation against an ARMA(1,1) process. Journal of the American Statistical Association 91, 1331–1342.Google Scholar
Arcones, M.A. &B., Yu (1994) Central limit theorems for empirical and U-processes of stationary mixing sequences. Journal of Theoretical Probability 7, 47–71.CrossRefGoogle Scholar
Berman, S.M. (1964) Limit theorems for the maximum term in stationary sequences. Annals of Mathematical Statistics 35, 502–516.CrossRefGoogle Scholar
Billingsley, P. (1995) Probability and Measure, 3rd Edition. Wiley.Google Scholar
Billingsley, P. (1999) Convergence of Probability Measures, 2nd Edition. Wiley.CrossRefGoogle Scholar
Boehme, T.K. &Rosenfeld, M. (1974)An example of two compact Hausdorff Fréchet spaces whose product is not Fréchet. Journal of the London Mathematical Society 8, 339–344.CrossRefGoogle Scholar
Box, G.E.P. &Pierce, D.A. (1970)Distribution of residual autocorrelations in autoregressive-integrated moving average time series models. Journal of the American Statistical Association 65, 1509–1526.CrossRefGoogle Scholar
Carrasco, M. &Chen, X. (2002)Mixing and moment properties of various GARCH and stochastic volatility models. Econometric Theory 18, 17–39.CrossRefGoogle Scholar
Chatterjee, S. (2005) An error bound in the Sudakov-Fernique inequality. Available at https://arxiv.org/abs/math/0510424.Google Scholar
Chernozhukov, V.,Chetverikov, D., &Kato, K. (2013)Gaussian approximations and multiplier bootstrap for maxima of sums of high-dimensional random vectors. Annals of Statistics 41, 2786–2819.CrossRefGoogle Scholar
Chernozhukov, V.,Chetverikov, D., &Kato, K. (2014) Testing many moment inequalities. Available at arXiv:1312.7614.Google Scholar
Chernozhukov, V.,Chetverikov, D., &Kato, K. (2015)Comparison and anti-concentration bounds for maxima of Gaussian random vectors. Probability Theory and Related Fields 162, 47–70.CrossRefGoogle Scholar
Chernozhukov, V.,Chetverikov, D., &Kato, K. (2017)Central limit theorems and bootstrap in high dimensions. Annals of Probability 45, 2309–2352.CrossRefGoogle Scholar
Chernozhukov, V.,Chetverikov, D., &Kato, K. (2018)Inference on causal and structural parameters using many moment inequalities. Review of Economic Studies 86, 1867–1900.CrossRefGoogle Scholar
Dalla, V.,Giraitis, L., &Phillips, P.C.B. (2019) Robust tests for white noise and cross-correlation. Cowles Foundation Discussion Paper CFDP 2194.CrossRefGoogle Scholar
Davidson, J. (1994) Stochastic Limit Theory. Oxford University Press.CrossRefGoogle Scholar
de Jong, R.M. (1997) Central limit theorems for dependent heterogeneous random variables. Econometric Theory 13, 353–367.CrossRefGoogle Scholar
Delgado, M.A.,Hidalgo, J., &Velasco, C. (2005) Distribution free goodness-of-fit tests for linear processes. Annals of Statistics 33, 2568–2609.CrossRefGoogle Scholar
Delgado, M.A. &Velasco, C. (2011) An asymptotically pivotal transform of the residuals sample autocorrelations with application to model checking. Journal of the American Statistical Association 106, 946–958.CrossRefGoogle Scholar
Deo, R.S. (2000) Spectral tests of the martingale hypothesis under conditional heteroscedasticity. Journal of Econometrics 99, 291–315.CrossRefGoogle Scholar
Drost, F.C. &Nijman, T.E. (1993) Temporal aggregation of GARCH processes. Econometrica 61, 909–927.CrossRefGoogle Scholar
Dudley, R.M. (1978) Central limit theorems for empirical measures. Annals of Probability 6, 899–929.CrossRefGoogle Scholar
Dudley, R.M. (1984) A course on empirical processes. Ecole d’Eté de Probabilités de Saint-Flour XII-1982. Lecture Notes in Math 1097, 2–142.Google Scholar
Dudley, R.M. &Philipp, W. (1983) “Invariance principles for sums of Banach space valued random elements and empirical processes. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete 62, 509–552.CrossRefGoogle Scholar
Escanciano, J.C. &Lobato, I.N. (2009) An automatic portmanteau test for serial correlation. Journal of Econometrics 151, 140–149.CrossRefGoogle Scholar
Francq, C. &Zakoïan, J.-M. (2004) Maximum likelihood estimation of pure GARCH and ARMA-GARCH processes. Bernoulli 10, 605–637.CrossRefGoogle Scholar
Francq, C. andZakoïan, J.-M. (2010) GARCH Models: Structure, Statistical Inference and Financial Applications. Wiley, UK.CrossRefGoogle Scholar
Gaenssler, P. &Ziegler, K. (1994) A uniform law of large numbers for set-indexed processes with applications to empirical and partial-sum processes. In Hoffmann-Jørgensen, J., Kuelbs, J., and Marcus, M.B. (eds.), Probability in Banach Spaces, vol. 9, pp.385–400. Birkhauser.CrossRefGoogle Scholar
Giné, E. &Zinn, J. (1990) Bootstrapping general empirical measures. Annals of Probability 18, 851–869.CrossRefGoogle Scholar
Grenander, U. &Rosenblatt, M. (1952) On spectral analysis of stationary time series. Proceedings of the National Academy of Sciences of the United States of America,38, 519–521.CrossRefGoogle ScholarPubMed
Guay, A.,Guerre, E., &Lazarová, S. (2013) Robust adaptive rate-optimal testing for the white noise hypothesis. Journal of Econometrics 176, 134–145.CrossRefGoogle Scholar
Hannan, E.J. (1974) The uniform convergence of autocovariances. Annals of Statistics 2, 803–806.CrossRefGoogle Scholar
Hansen, B.E. (1996) Inference when a nuisance parameter is not identified under the null hypothesis. Econometrica 64, 413–430.CrossRefGoogle Scholar
Hoffmann-Jørgensen, J. (1984) Convergence of Stochastic Processes on Polish Spaces. (mimeo).Google Scholar
Hoffmann-Jørgensen, J. (1991) Convergence of stochastic processes on Polish spaces. InVarious Publications Series 39. Aarhus Universitet, Aarhus, Denmark (mimeo).Google Scholar
Hong, Y. (1996) Consistent testing for serial correlation of unknown form. Econometrica 64, 837–864.CrossRefGoogle Scholar
Hong, Y. (2001) A test for volatility spillover with application to exchange rates. Journal of Econometrics 103, 183–224.CrossRefGoogle Scholar
Horowitz, J.L.,Lobato, I.N.,Nankervis, J.C., andSavin, N.E. (2006) Bootstrapping the Box-Pierce Q test: A robust test of uncorrelatedness. Journal of Econometrics 133, 841–862.CrossRefGoogle Scholar
Hüsler, J. (1986) Extreme values of non-stationary random sequences. Journal of Applied Probability 23, 937–950.CrossRefGoogle Scholar
Inglot, T. &Ledwina, T. (2006) Towards data driven selection of a penalty function for data driven Neyman tests. Linear Algebra and its Applications 417, 124–133.CrossRefGoogle Scholar
Jirak, M. (2011) On the maximum of covariance estimators. Journal of Multivariate Analysis 102, 1032–1046.CrossRefGoogle Scholar
Kolmogorov, A.N. &Rozanov, Y.A. (1960) On strong mixing conditions for stationarity Gaussian processes. Theory of Probability and its Applications 5, 204–208.CrossRefGoogle Scholar
Kuan, C.-M. &Lee, W.-M. (2006) Robust M tests without consistent estimation of the asymptotic covariance matrix. Journal of the American Statistical Association 101, 1264–1275.CrossRefGoogle Scholar
Kullback, S. &Leibler, R.A. (1951) On information and sufficiency. Annals of Mathematical Statistics 22, 79–86.CrossRefGoogle Scholar
Le Cam, L. (1988) On the Prokhorov distance between the empirical process and the associated Gaussian bridge.” Discussion Paper, Dept. of Statistics, University of California, Berkely, CA.Google Scholar
Leadbetter, M.R.,Lindgren, G., &Rootzén, H. (1983) Extremes and Related Properties of Random Sequences and Processes, Springer Series in Statistics. Springer-Verlag New York.CrossRefGoogle Scholar
Lee, S.-W. &Hansen, B.E. (1994) Asymptotic theory for the GARCH(1,1) quasi-maximum likelihood estimator. Econometric Theory 10, 29–52.CrossRefGoogle Scholar
Lipschitz, S. (1965) General Topology. McGraw Hill.Google Scholar
Liu, R.Y. (1988) Bootstrap procedures under some non-I.I.D. models. Annals of Statistics 16, 1696–1708.CrossRefGoogle Scholar
Ljung, G.M. &Box, G.E.P. (1978) On a measure of lack of fit in time series models. Biometrika 65, 297–303.CrossRefGoogle Scholar
Lobato, I.N. (2001) Testing that a dependent process is uncorrelated. Journal of the American Statistical Association 96, 1066–1076.CrossRefGoogle Scholar
Lobato, I.N.,Nankervis, J.C., &Savin, N.E. (2002) Testing for zero autocorrelation in the presence of statistical dependence. Econometric Theory 18, 730–743.CrossRefGoogle Scholar
McLeish, D.L. (1975) A maximal inequality and dependent strong laws. Annals of Probability 3, 829–839.CrossRefGoogle Scholar
Meitz, M. &Saikkonen, P. (2011) Parameter estimation in nonlinear AR-GARCH models. Econometric Theory 27, 1236–1278.CrossRefGoogle Scholar
Myers, J.S. (2002) The minimum number of monotone subsequences.”The Electronic Journal of Combinatorics 9, R4.CrossRefGoogle Scholar
Nankervis, J.C. &Savin, N.E. (2010) Testing for serial correlation: Generalized Andrews-Ploberger tests. Journal of Business & Economic Statistics 28, 246–255.CrossRefGoogle Scholar
Nankervis, J.C. &Savin, N.E. (2012) Testing for uncorrelated errors in ARMA models: Non-standard Andrews-Ploberger tests. Econometrics Journal 15, 516–534.CrossRefGoogle Scholar
Nelson, D.B. (1990) Stationarity and persistence in the GARCH(1,1) model.”Econometric Theory 6, 318–334.CrossRefGoogle Scholar
Neyman, J. (1937) “Smootht est for goodness of fit. Scandinavian Aktuarietidskr 20, 149–199.Google Scholar
Pakes, A. &Pollard, D. (1989) Simulation and the asymptotics of optimization estimators. Econometrica 57, 1027–1057.CrossRefGoogle Scholar
Politis, D.N. &Romano, J.P. (1994) Limit theorems for weakly dependent Hilbert space valued random variables with application to the stationary bootstrap. Statistica Sinica 4, 461–476.Google Scholar
Pollard, D. (1984) Convergence of Stochastic Processes. Springer-Verlag New York.CrossRefGoogle Scholar
Pollard, D. (1990) Empirical processes: Theory and applications. InNSF-CBMS Regional Conference Series in Probability and Statistics, p.2.Google Scholar
Portnoy, S. (1986) On the central limit theorem in R p when $p \rightarrow \infty.$ Probability Theory and Related Fields 73, 571–583.CrossRefGoogle Scholar
Ramsey, F.P. (1930) On a problem of formal logic. Proceedings of the London Mathematical Society 30, 264–286.CrossRefGoogle Scholar
Romano, J.P. &Thombs, L.A. (1996) Inference for Autocorrelations under Weak Assumptions. Journal of the American Statistical Association 91, 590–600.CrossRefGoogle Scholar
Sawa, T. (1978) Information criteria for discriminating among alternative regression models. Econometrica 46, 1273–1291.CrossRefGoogle Scholar
Shao, X. (2010) The dependent wild bootstrap. Journal of the American Statistical Association 105, 218–235.CrossRefGoogle Scholar
Shao, X. (2011) A bootstrap-assisted spectral test of white noise under unknown dependence. Journal of Econometrics 162, 213–224.CrossRefGoogle Scholar
Shao, X. &Wu, W.B. (2007) Asymptotic spectral theory for nonlinear time series. Annals of Statistics 35, 1773–1801.CrossRefGoogle Scholar
Straumann, D. &Mikosch, T. (2006) Quasi-maximum-likelihood estimation in conditionally heteroscedastic time series: A stochastic recurrence equations approach. Annals of Statistics 34, 5.CrossRefGoogle Scholar
Thomason, A. (1988) A disproof of a conjecture of Erdös in Ramsey theory.”Journal of the London Mathematical Society 39, 246–255.Google Scholar
Wu, C.F.J. (1986) Jackknife, bootstrap and other resampling methods in regression analysis. Annals of Statistics 14, 1261–1295.Google Scholar
Wu, W.B. (2005) Nonlinear system theory: Another look at dependence. Proceedings of the National Academy of Sciences of the United States of America 102, 14150–14154.CrossRefGoogle Scholar
Wu, W.B. &Min, W. (2005) On linear processes with dependent innovations. Stochastic Processes and their Applications 115, 939–958.Google Scholar
Xiao, H. &Wu, W.B. (2014) Portmanteau test and simultaneous inference for serial covariances. Statistica Sinica 24, 577–599.Google Scholar
Yurinskii, V.V. (1977) On the error of the Gaussian approximation for convolutions. Theory of Probability and its Applications 22, 236–247.CrossRefGoogle Scholar
Zhang, D. &Wu, W.B. (2017) Gaussian approximation for high dimensional time series. Annals of Statistics 45, 1895–1919.CrossRefGoogle Scholar
Zhang, X. &Cheng, G. (2014) Bootstrapping high dimensional time series. Available at arXiv:1406.1037.Google Scholar
Zhu, K. (2015) Bootstrapping the Portmanteau tests in weak auto-regressive moving average models. Journal of the Royal Statistical Society Series B 78, 463–485.CrossRefGoogle Scholar
Zhu, K. &Li, W.K. (2015) A bootstrapped spectral test for adequacy in weak ARMA models. Journal of Econometrics 187, 113–130.CrossRefGoogle Scholar
Supplementary material: File

Hill and Motegi supplementary material

Hill and Motegi supplementary material 1

Download Hill and Motegi supplementary material(File)
File 288.1 KB
Supplementary material: PDF

Hill and Motegi supplementary material

Hill and Motegi supplementary material 2

Download Hill and Motegi supplementary material(PDF)
PDF 872.9 KB