Hostname: page-component-848d4c4894-pftt2 Total loading time: 0 Render date: 2024-04-30T12:16:02.827Z Has data issue: false hasContentIssue false
  • English
  • Français

CHARACTERIZATION OF THE TAIL BEHAVIOR OF A CLASS OF BEKK PROCESSES: A STOCHASTIC RECURRENCE EQUATION APPROACH

Published online by Cambridge University Press:  04 February 2021

Muneya Matsui  and
Rasmus Søndergaard Pedersen
Muneya Matsui
Affiliation:
Nanzan University
Rasmus Søndergaard Pedersen*
Affiliation:
University of Copenhagen
*
Address correspondence to Rasmus Søndergaard Pedersen, Department of Economics, University of Copenhagen, Øster Farimagsgade 5, DK-1353 Copenhagen K, Denmark; e-mail: rsp@econ.ku.dk.
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider conditions for strict stationarity and ergodicity of a class of multivariate BEKK processes 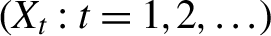$(X_t : t=1,2,\ldots )$ and study the tail behavior of the associated stationary distributions. Specifically, we consider a class of BEKK-ARCH processes where the innovations are assumed to be Gaussian and a finite number of lagged 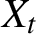$X_t$ ’s may load into the conditional covariance matrix of 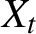$X_t$ . By exploiting that the processes have multivariate stochastic recurrence equation representations, we show the existence of strictly stationary solutions under mild conditions, where only a fractional moment of 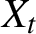$X_t$ may be finite. Moreover, we show that each component of the BEKK processes is regularly varying with some tail index. In general, the tail index differs along the components, which contrasts with most of the existing literature on the tail behavior of multivariate GARCH processes. Lastly, in an empirical illustration of our theoretical results, we quantify the model-implied tail index of the daily returns on two cryptocurrencies.

Type
ARTICLES
Information
Econometric Theory , Volume 38 , Issue 1 , February 2022 , pp. 1 - 34
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

We thank Peter C.B. Phillips (editor), Robert Taylor (co-editor), and two referees for helpful comments and suggestions that have led to a much improved paper. Moreover, we thank Ewa Damek, Rustam Ibragimov, Anders Rahbek, and participants at the 2019 CFE Conference for valuable suggestions. Matsui’s research is partly supported by the JSPS Grant-in-Aid for Young Scientists B (16k16023) and for Scientific Research C (19K11868). Pedersen is grateful for support from the Carlsberg Foundation (CF16-0909, ”Robust methods for volatility modelling”).

References

REFERENCES

Alsmeyer, G. & Mentemeier, S. (2012) Tail behavior of stationary solutions of random difference equations: The case of regular matrices. Journal of Differential Equations and Applications 18, 1305–1332.CrossRefGoogle Scholar
Avarucci, M., Beutner, E., & Zaffaroni, P. (2013) On moment conditions for quasi-maximum likelihood estimation of multivariate ARCH models. Econometric Theory 29, 545–566.CrossRefGoogle Scholar
Basrak, B. & Segers, J. (2009) Regularly varying multivariate time series. Stochastic Processes and Their Applications 119, 1055–1080.CrossRefGoogle Scholar
Bougerol, P. & Picard, N. (1992) Strict stationarity of generalized autoregressive processes. Annals of Probability 20, 1714–1730.CrossRefGoogle Scholar
Boussama, F., Fuchs, F., & Stelzer, R. (2011) Stationarity and geometric ergodicity of BEKK multivariate GARCH models. Stochastic Processes and Their Applications 121, 2331–2360.CrossRefGoogle Scholar
Brandt, A. (1986) The stochastic equation Yn+1 = An Yn + Bn with stationary coefficients. Advances in Applied Probability 18, 211–220.Google Scholar
Breiman, L. (1965) On some limit theorems similar to the arc-sin law. Theory of Probability and Its Applications 10, 323–331.CrossRefGoogle Scholar
Boussama, F., Fuchs, F., & Stelzer, R. (2011) Stationarity and geometric ergodicity of BEKK multivariate GARCH models. Stochastic Processes and Their Applications 121, 2331–2360.CrossRefGoogle Scholar
Buraczewski, D., Damek, E., Guivarc’h, Y., Hulanicki, A., & Urban, R. (2009) Tail-homogeneity of stationary measures for some multidimensional stochastic recursions. Probability Theory and Related Fields 145, 385–420.CrossRefGoogle Scholar
Buraczewski, D., Damek, E., & Mikosch, T. (2016) Stochastic Models with Power-Law Tails: The Equation X = AX + B. Springer Series in Operations Research and Financial Engineering, Springer International Publishing.CrossRefGoogle Scholar
Cont, R. (2001) Empirical properties of asset returns: Stylized facts and statistical issues. Quantitative Finance 1, 223–236.CrossRefGoogle Scholar
Damek, E., Matsui, M., & Świątkowski, W. (2019) Componentwise different tail solutions for bivariate stochastic recurrence equations with application to GARCH(1,1) processes. Colloquium Mathematicum 155, 227–254.CrossRefGoogle Scholar
Damek, E. & Matsui, M. (2019) Tails of bivariate stochastic recurrence equation, in preparation.Google Scholar
Damek, E. & Zienkiewicz, J. (2018) Affine stochastic equation with triangular matrices. Journal of Differential Equations and Applications 24, 520–542.CrossRefGoogle Scholar
Davis, R.A. & Mikosch, T. (2009) Extreme value theory for GARCH processes. In Andersen, T.G., Davis, R.A., Kreiß, J.-P., & Mikosch, T. (eds.), Handbook of Financial Time Series, pp. 186–200. Springer.Google Scholar
Engle, R.F. & Kroner, K.F. (1995) Multivariate simultaneous generalized ARCH. Econometric Theory 11, 122–150.CrossRefGoogle Scholar
Francq, C. & Zakoïan, J.-M. (2010) GARCH Models: Structure, Statistical Inference and Financial Applications. John Wiley & Sons.CrossRefGoogle Scholar
Gabaix, X. (2009) Power laws in economics and finance. The Annual Review of Economics 1, 255–293.CrossRefGoogle Scholar
Gabaix, X. & Ibragimov, R. (2011) Rank—1/2: A simple way to improve the OLS estimation of tail exponents. Journal of Business & Economic Statistics 29, 24–39.CrossRefGoogle Scholar
Gerencsér, L., Michaletzky, G., & Orlovits, Z. (2008) Stability of block-triangular stationary random matrices. Systems & Control Letters 57, 620–625.CrossRefGoogle Scholar
Goldie, C.M. (1991) Implicit renewal theory and tails of solutions of random equations. Annals of Applied Probability 1, 126–166.CrossRefGoogle Scholar
Guivarc’h, Y. & Le Page, É. (2016) Spectral gap properties for linear random walks and Pareto’s asymptotics for affine stochastic recursions. Annales de l’Institut Henri Poincaré (B) Probabilités et Statistiques 52, 503–574.Google Scholar
Hafner, C. & Preminger, A. (2009) On asymptotic theory for multivariate GARCH models. Journal of Multivariate Analysis 100, 2044–2054.CrossRefGoogle Scholar
Horn, R.A. & Johnson, C.R. (2013) Matrix Analysis, 2nd Edition, Cambridge University Press.Google Scholar
Ibragimov, M., Ibragimov, R., & Walden, J. (2015) Heavy-Tailed Distributions and Robustness in Economics and Finance, Lecture Notes in Statistics, 214. Springer International Publishing.CrossRefGoogle Scholar
Krengel, U. (2011) Ergodic Theorems, vol. 6. Walter de Gruyter.Google Scholar
Ling, S. & Li, D. (2008) Asymptotic inference for a nonstationary double AR(1) model. Biometrika 95, 257–263.CrossRefGoogle Scholar
Loretan, M. & Phillips, P.C.B. (1994) Testing for covariance stationarity of heavy-tailed time series. Journal of Empirical Finance 1, 211–248.CrossRefGoogle Scholar
Matsui, M. & Mikosch, T. (2016) The extremogram and the cross-extremogram for a bivariate GARCH(1,1) process. Advances in Applied Probability 48A, 217–233.CrossRefGoogle Scholar
Matsui, M. & Świątkowski, W., Tail indices for AX+B recursion with triangular matrices. Journal of Theoretical Probability, first published online 29 July 2020. doi: https://doi.org/10.1007/s10959-020-01019-8.CrossRefGoogle Scholar
Nelson, D.B. (1990) Stationarity and persistence in the GARCH(1,1) model. Econometric Theory 6, 318–334.CrossRefGoogle Scholar
Nicholls, D.F. & Quinn, B.G. (1982) Random Coefficient Autoregressive Models: An Introduction, Lecture Notes in Statistics, 11. Springer.CrossRefGoogle Scholar
Nielsen, H.B. & Rahbek, A. (2014) Unit root vector autoregression with volatility induced stationarity. Journal of Empirical Finance 29, 144–167.CrossRefGoogle Scholar
Pedersen, R.S. (2016) Targeting estimation of CCC-GARCH models with infinite fourth moments. Econometric Theory 32, 498–531.CrossRefGoogle Scholar
Pedersen, R.S. & Rahbek, A. (2014) Multivariate variance targeting in the BEKK-GARCH model. The Econometrics Journal 17, 24–55.CrossRefGoogle Scholar
Pedersen, R.S. & Wintenberger, O. (2018) On the tail behavior of a class of multivariate conditionally heteroskedastic processes. Extremes 21, 261–284.CrossRefGoogle Scholar
Resnick, S.I. (2007) Heavy-Tail Phenomena: Probabilistic and Statistical Modeling. Springer.Google Scholar
Stărică, C. (1999) Multivariate extremes for models with constant conditional correlations. Journal of Empirical Finance 6, 515–553.CrossRefGoogle Scholar
Straumann, D. (2005) Estimation in Conditionally Heteroscedastic Time Series Models, Lecture Notes in Statistics, 181, Springer-Verlag.Google Scholar
Sun, P. & Zhou, C. (2014) Diagnosing the distribution of GARCH innovations. Journal of Empirical Finance 29, 287–303.CrossRefGoogle Scholar
Tsay, R.S. (1987) Conditional heteroscedastic time series models. Journal of the American Statistical Association 82, 590–604.CrossRefGoogle Scholar