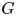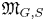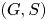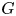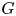1. Introduction
1.1 Informal context
Noether's approach to symmetries and conserved quantities in classical mechanics naturally gives rise to quotient constructions in symplectic geometry. The most basic of these constructions is Marsden–Weinstein–Meyer reduction [Reference MeyerMey73, Reference Marsden and WeinsteinMW74] for Hamiltonian Lie group actions, a cornerstone of symplectic geometry [Reference Guillemin and SternbergGS82a, Reference Sjamaar and LermanSL91, Reference SjamaarSja95, Reference Meinrenken and SjamaarMS99] with wide-ranging implications for algebraic geometry [Reference Atiyah and BottAB83, Reference KirwanKir84, Reference HitchinHit87, Reference LosevLos09] and geometric representation theory [Reference Kazhdan, Kostant and SternbergKKS78, Reference NakajimaNak98, Reference Etingof and GinzburgEG02, Reference Gan and GinzburgGG04, Reference Bezrukavnikov, Finkelberg and MirkovićBFM05, Reference Braverman, Finkelberg and NakajimaBFN19, Reference BălibanuBăl21]. This construction applies to a Hamiltonian ![]() $G$-space, i.e. a symplectic manifold
$G$-space, i.e. a symplectic manifold ![]() $M$ equipped with a Hamiltonian action of a Lie group
$M$ equipped with a Hamiltonian action of a Lie group ![]() $G$ and a moment map
$G$ and a moment map ![]() $\mu :M\longrightarrow \mathfrak {g}^{*}$, where
$\mu :M\longrightarrow \mathfrak {g}^{*}$, where ![]() $\mathfrak {g}$ is the Lie algebra of
$\mathfrak {g}$ is the Lie algebra of ![]() $G$. Each element
$G$. Each element ![]() $\xi \in \mathfrak {g}^{*}$ has a
$\xi \in \mathfrak {g}^{*}$ has a ![]() $G$-stabilizer
$G$-stabilizer ![]() $G_{\xi }\subseteq G$ and determines a topological quotient
$G_{\xi }\subseteq G$ and determines a topological quotient
called the Marsden–Weinstein–Meyer reduction of ![]() $M$ by
$M$ by ![]() $G$ at level
$G$ at level ![]() $\xi$. The space
$\xi$. The space ![]() $M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{\xi }} G$ is a symplectic manifold under certain hypotheses.
$M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{\xi }} G$ is a symplectic manifold under certain hypotheses.
Motivated by recent advances in topological quantum field theory [Reference Moore and TachikawaMT12, Reference Ginzburg and KazhdanGK], we introduce and study a generalization of Marsden–Weinstein–Meyer reduction. Our starting point is the work of Mikami–Weinstein [Reference Mikami and WeinsteinMW88], which defines the notion of a Hamiltonian action of a symplectic groupoid ![]() $\mathcal {G} \rightrightarrows X$ on a symplectic manifold
$\mathcal {G} \rightrightarrows X$ on a symplectic manifold ![]() $M$ with moment map
$M$ with moment map ![]() $\mu : M \longrightarrow X$. These authors proceed to define the symplectic reduction
$\mu : M \longrightarrow X$. These authors proceed to define the symplectic reduction ![]() $M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{x}} \mathcal {G} := \mu ^{-1}(x) / \mathcal {G}_x$ of
$M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{x}} \mathcal {G} := \mu ^{-1}(x) / \mathcal {G}_x$ of ![]() $M$ by
$M$ by ![]() $\mathcal {G}$ at level
$\mathcal {G}$ at level ![]() $x \in X$, where
$x \in X$, where ![]() $\mathcal {G}_x$ is the isotropy group at
$\mathcal {G}_x$ is the isotropy group at ![]() $x$. Our construction upgrades the level
$x$. Our construction upgrades the level ![]() $x \in X$ and subgroup
$x \in X$ and subgroup ![]() $\mathcal {G}_{x} \subseteq \mathcal {G}$ to a submanifold
$\mathcal {G}_{x} \subseteq \mathcal {G}$ to a submanifold ![]() $S \subseteq X$ and subgroupoid
$S \subseteq X$ and subgroupoid ![]() $\mathcal {G}_S \subseteq \mathcal {G}$, respectively, in such a way that the quotient
$\mathcal {G}_S \subseteq \mathcal {G}$, respectively, in such a way that the quotient ![]() $M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S}} \mathcal {G} := \mu ^{-1}(S) / \mathcal {G}_S$ is a symplectic manifold.
$M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S}} \mathcal {G} := \mu ^{-1}(S) / \mathcal {G}_S$ is a symplectic manifold.
The equivalence between usual Hamiltonian ![]() $G$-spaces and Hamiltonian spaces for the cotangent groupoid
$G$-spaces and Hamiltonian spaces for the cotangent groupoid ![]() $T^{*}G\rightrightarrows \mathfrak {g}^{*}$ (see [Reference Mikami and WeinsteinMW88]) then allows us to generalize (1.1) by replacing the level
$T^{*}G\rightrightarrows \mathfrak {g}^{*}$ (see [Reference Mikami and WeinsteinMW88]) then allows us to generalize (1.1) by replacing the level ![]() $\xi \in \mathfrak {g}^{*}$ with a submanifold
$\xi \in \mathfrak {g}^{*}$ with a submanifold ![]() $S\subseteq \mathfrak {g}^{*}$. In other words, given a Hamiltonian
$S\subseteq \mathfrak {g}^{*}$. In other words, given a Hamiltonian ![]() $G$-space
$G$-space ![]() $M$ with moment map
$M$ with moment map ![]() $\mu : M \longrightarrow \mathfrak {g}^{*}$, we obtain a notion of symplectic reduction
$\mu : M \longrightarrow \mathfrak {g}^{*}$, we obtain a notion of symplectic reduction
of ![]() $M$ by
$M$ by ![]() $G$ at level
$G$ at level ![]() $S \subseteq \mathfrak {g}^{*}$, where
$S \subseteq \mathfrak {g}^{*}$, where ![]() $\mathcal {G}_S$ is a certain subgroupoid of
$\mathcal {G}_S$ is a certain subgroupoid of ![]() $T^{*}G$ determined by
$T^{*}G$ determined by ![]() $S$. As with (1.1), the space (1.2) is a symplectic manifold under reasonable hypotheses. As
$S$. As with (1.1), the space (1.2) is a symplectic manifold under reasonable hypotheses. As ![]() $\mathcal {G}_S$ replaces the stabilizer subgroup
$\mathcal {G}_S$ replaces the stabilizer subgroup ![]() $G_\xi$ in (1.1), we call it the ‘stabilizer subgroupoid’ of
$G_\xi$ in (1.1), we call it the ‘stabilizer subgroupoid’ of ![]() $S$.
$S$.
To be somewhat more precise, let us address the class of submanifolds ![]() $S\subseteq X$ for which our construction can be performed; these are the so-called pre-Poisson submanifolds of
$S\subseteq X$ for which our construction can be performed; these are the so-called pre-Poisson submanifolds of ![]() $X$, as defined and studied by Cattaneo and Zambon [Reference Cattaneo and ZambonCZ07, Reference Cattaneo and ZambonCZ09]. Poisson transversals and Poisson submanifolds are automatically pre-Poisson, and there is a reasonable sense in which generic submanifolds of
$X$, as defined and studied by Cattaneo and Zambon [Reference Cattaneo and ZambonCZ07, Reference Cattaneo and ZambonCZ09]. Poisson transversals and Poisson submanifolds are automatically pre-Poisson, and there is a reasonable sense in which generic submanifolds of ![]() $X$ are pre-Poisson. At the same time, each pre-Poisson submanifold
$X$ are pre-Poisson. At the same time, each pre-Poisson submanifold ![]() $S\subseteq X$ canonically determines a Lie subalgebroid
$S\subseteq X$ canonically determines a Lie subalgebroid ![]() $L_S \longrightarrow S$ of the Lie algebroid of
$L_S \longrightarrow S$ of the Lie algebroid of ![]() $\mathcal {G}$. The notion of a stabilizer subgroupoid for
$\mathcal {G}$. The notion of a stabilizer subgroupoid for ![]() $S$ is then transparent; it refers to any isotropic immersed Lie subgroupoid
$S$ is then transparent; it refers to any isotropic immersed Lie subgroupoid ![]() $\mathcal {H}\rightrightarrows S$ of
$\mathcal {H}\rightrightarrows S$ of ![]() $\mathcal {G}$ integrating
$\mathcal {G}$ integrating ![]() $L_S$. One has a non-empty, discrete family of stabilizer subgroupoids for
$L_S$. One has a non-empty, discrete family of stabilizer subgroupoids for ![]() $S$, exactly one of which is source-connected and source-simply-connected (ssc).
$S$, exactly one of which is source-connected and source-simply-connected (ssc).
Our generalization of Marsden–Weinstein–Meyer reduction amounts to the topological space
being a symplectic manifold under reasonable hypotheses, where ![]() $\mu :M\longrightarrow X$ is the moment map. Any two source-connected choices of
$\mu :M\longrightarrow X$ is the moment map. Any two source-connected choices of ![]() $\mathcal {H}\rightrightarrows S$ yield the same quotient
$\mathcal {H}\rightrightarrows S$ yield the same quotient ![]() $M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S,\mathcal {H}}}\mathcal {G}$, allowing us to define
$M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S,\mathcal {H}}}\mathcal {G}$, allowing us to define
We use the nomenclature symplectic reduction along a submanifold for the construction described in these last two sentences. In very general terms, the following are some features that it enjoys. The reader is referred to § 1.2 for more precise descriptions of these features.
Categories
Our construction has analogs in the categories of complex analytic spaces, complex algebraic varieties, and derived Artin stacks, all of which are developed and proved in this paper.
Relation to other constructions
Several well-studied quotient constructions in symplectic geometry can be realized as special cases of symplectic reduction along a submanifold. Such constructions include Marsden–Weinstein–Meyer reduction, Mikami–Weinstein reduction for Hamiltonian symplectic groupoid actions [Reference Mikami and WeinsteinMW88], the pre-images of Poisson transversals under moment maps [Reference BielawskiBie97, Reference Frejlich and MarcutFM17, Reference Crooks and RöserCR20, Reference Crooks and van PruijssenCP21], and the Ginzburg–Kazhdan presentation [Reference Ginzburg and KazhdanGK] of Moore–Tachikawa varieties [Reference Moore and TachikawaMT12]. We also find that symplectic cutting [Reference LermanLer95, Reference Lerman, Meinrenken, Tolman and WoodwardLMTW98, Reference WeitsmanWei01, Reference Martens and ThaddeusMT12, Reference Fisher and RayanFR16] and symplectic implosion [Reference Guillemin, Jeffrey and SjamaarGJS02, Reference Dancer, Kirwan and SwannDKS13, Reference Dancer, Kirwan and RöserDKR16, Reference SafronovSaf17] may be described more simply as reduction along a polyhedral set and reduction along a closed Weyl chamber, respectively. Our work also has an interpretation in shifted symplectic geometry [Reference Pantev, Toën, Vaquié and VezzosiPTVV13] as a derived intersection of two Lagrangians.
Universal reduced spaces
Our construction yields a very simple, systematic, Lie-theoretic technique for producing Hamiltonian Lie group spaces. One begins with a Lie group ![]() $G$ and pre-Poisson submanifold
$G$ and pre-Poisson submanifold ![]() $S\subseteq \mathfrak {g}^{*}$, e.g.
$S\subseteq \mathfrak {g}^{*}$, e.g. ![]() $S$ could be any
$S$ could be any ![]() $G$-invariant submanifold or any Poisson transversal. If the pair
$G$-invariant submanifold or any Poisson transversal. If the pair ![]() $(G,S)$ satisfies some non-degeneracy conditions, we show that it determines a universal Hamiltonian
$(G,S)$ satisfies some non-degeneracy conditions, we show that it determines a universal Hamiltonian ![]() $G$-space
$G$-space ![]() $\mathfrak {M}_{G, S}$; the precise meaning of ‘universal’ is given in § 1.2.
$\mathfrak {M}_{G, S}$; the precise meaning of ‘universal’ is given in § 1.2.
We realize several Hamiltonian ![]() $G$-spaces in this way, including products of coadjoint orbits, open Moore–Tachikawa varieties [Reference BielawskiBie21, Reference Ginzburg and KazhdanGK], universal imploded cross-sections [Reference Guillemin, Jeffrey and SjamaarGJS02], and some spaces that appear to be new. We also show
$G$-spaces in this way, including products of coadjoint orbits, open Moore–Tachikawa varieties [Reference BielawskiBie21, Reference Ginzburg and KazhdanGK], universal imploded cross-sections [Reference Guillemin, Jeffrey and SjamaarGJS02], and some spaces that appear to be new. We also show ![]() $\mathfrak {M}_{G,S}$ to be a symplectic groupoid when
$\mathfrak {M}_{G,S}$ to be a symplectic groupoid when ![]() $S\subseteq \mathfrak {g}^{*}$ is
$S\subseteq \mathfrak {g}^{*}$ is ![]() $G$-invariant and appropriate non-degeneracy conditions are imposed.
$G$-invariant and appropriate non-degeneracy conditions are imposed.
Remark 1.1 Some follow-up work (by Bălibanu and Mayrand) will address a few generalizations of our construction in the smooth category; it will concern Hamiltonian actions of quasi-symplectic groupoids on Dirac manifolds, as well as quotients by more general subgroupoids.
1.2 Statement of main results
We now give precise formulations of our main results.
1.2.1 The smooth category
Let ![]() $(X,\sigma )$ be a Poisson manifold with Poisson bivector field
$(X,\sigma )$ be a Poisson manifold with Poisson bivector field ![]() $\sigma :T^{*}X\longrightarrow TX$. A submanifold
$\sigma :T^{*}X\longrightarrow TX$. A submanifold ![]() $S\subseteq X$ is called pre-Poisson if
$S\subseteq X$ is called pre-Poisson if ![]() $\sigma ^{-1}(TS)\cap TS^{\circ }$ has constant rank over
$\sigma ^{-1}(TS)\cap TS^{\circ }$ has constant rank over ![]() $S$, where
$S$, where ![]() $TS^{\circ }\subseteq T^{*}X$ is the annihilator of
$TS^{\circ }\subseteq T^{*}X$ is the annihilator of ![]() $TS\subseteq TX$. Any symplectic groupoid
$TS\subseteq TX$. Any symplectic groupoid ![]() $\mathcal {G}\rightrightarrows X$ has the property that
$\mathcal {G}\rightrightarrows X$ has the property that ![]() $X$ is Poisson, and we may therefore consider a pre-Poisson submanifold
$X$ is Poisson, and we may therefore consider a pre-Poisson submanifold ![]() $S\subseteq X$. One then has a Lie subalgebroid
$S\subseteq X$. One then has a Lie subalgebroid
of the Lie algebroid of ![]() $\mathcal {G}\rightrightarrows X$. We use the term stabilizer subgroupoid of
$\mathcal {G}\rightrightarrows X$. We use the term stabilizer subgroupoid of ![]() $S$ for any isotropic Lie subgroupoidFootnote 1
$S$ for any isotropic Lie subgroupoidFootnote 1 ![]() $\mathcal {H}\rightrightarrows S$ of
$\mathcal {H}\rightrightarrows S$ of ![]() $\mathcal {G}\rightrightarrows X$ having
$\mathcal {G}\rightrightarrows X$ having ![]() $L_S$ as its Lie algebroid.
$L_S$ as its Lie algebroid.
On the other hand, Mikami and Weinstein [Reference Mikami and WeinsteinMW88] define what it means for ![]() $\mathcal {G}\rightrightarrows X$ to act in a Hamiltonian fashion on a symplectic manifold
$\mathcal {G}\rightrightarrows X$ to act in a Hamiltonian fashion on a symplectic manifold ![]() $(M,\omega )$. Any stabilizer subgroupoid
$(M,\omega )$. Any stabilizer subgroupoid ![]() $\mathcal {H}\rightrightarrows S$ then acts on
$\mathcal {H}\rightrightarrows S$ then acts on ![]() $N:= \mu ^{-1}(S)$, where
$N:= \mu ^{-1}(S)$, where ![]() $\mu :M\longrightarrow X$ is the moment map realizing the Hamiltonian action of
$\mu :M\longrightarrow X$ is the moment map realizing the Hamiltonian action of ![]() $\mathcal {G}\rightrightarrows X$ on
$\mathcal {G}\rightrightarrows X$ on ![]() $M$. We call the quotient topological space
$M$. We call the quotient topological space
the symplectic reduction of ![]() $M$ by
$M$ by ![]() $\mathcal {G}$ along
$\mathcal {G}$ along ![]() $S$ with respect to
$S$ with respect to ![]() $\mathcal {H}$. This space features in the following result.
$\mathcal {H}$. This space features in the following result.
Theorem A (Smooth category)
Suppose that a symplectic groupoid ![]() $\mathcal {G}\rightrightarrows X$ acts on a symplectic manifold
$\mathcal {G}\rightrightarrows X$ acts on a symplectic manifold ![]() $(M,\omega )$ in a Hamiltonian fashion with moment map
$(M,\omega )$ in a Hamiltonian fashion with moment map ![]() $\mu :M\longrightarrow X$. Let
$\mu :M\longrightarrow X$. Let ![]() $\mathcal {H}\rightrightarrows S$ be a stabilizer subgroupoid of a pre-Poisson submanifold
$\mathcal {H}\rightrightarrows S$ be a stabilizer subgroupoid of a pre-Poisson submanifold ![]() $S\subseteq X$ and set
$S\subseteq X$ and set ![]() $N:= \mu ^{-1}(S)$.
$N:= \mu ^{-1}(S)$.
(i) Assume that
 $S$ intersects
$S$ intersects  $\mu$ cleanly and that
$\mu$ cleanly and that  $M\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S,\mathcal {H}}}\mathcal {G} := N / \mathcal {H}$ has a smooth manifold structure for which the quotient map
$M\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S,\mathcal {H}}}\mathcal {G} := N / \mathcal {H}$ has a smooth manifold structure for which the quotient map  $\pi :N\longrightarrow M\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S,\mathcal {H}}}\mathcal {G}$ is a submersion. The manifold
$\pi :N\longrightarrow M\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S,\mathcal {H}}}\mathcal {G}$ is a submersion. The manifold  $M\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S,\mathcal {H}}}\mathcal {G}$ then carries a unique symplectic form
$M\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S,\mathcal {H}}}\mathcal {G}$ then carries a unique symplectic form  $\bar {\omega }$ for which
where
$\bar {\omega }$ for which
where \begin{align*} \pi^{*}\bar{\omega}=i^{*}\omega, \end{align*}
\begin{align*} \pi^{*}\bar{\omega}=i^{*}\omega, \end{align*} $i:N\longrightarrow M$ is the inclusion map.
$i:N\longrightarrow M$ is the inclusion map.(ii) If
 $\mathcal {H}$ acts freely on
$\mathcal {H}$ acts freely on  $N$, then
$N$, then  $S$ is transverse to
$S$ is transverse to  $\mu$. The hypotheses of part (i) are therefore satisfied if
$\mu$. The hypotheses of part (i) are therefore satisfied if  $\mathcal {H}$ acts freely and properly on
$\mathcal {H}$ acts freely and properly on  $N$.
$N$.(iii) Let
 $\sigma :T^{*}X\longrightarrow TX$ denote the Poisson bivector field on
$\sigma :T^{*}X\longrightarrow TX$ denote the Poisson bivector field on  $X$. Assume that the hypotheses of part (i) are satisfied and that
$X$. Assume that the hypotheses of part (i) are satisfied and that  $S/\mathcal {H}$ has a smooth manifold structure for which the quotient map
$S/\mathcal {H}$ has a smooth manifold structure for which the quotient map  $\rho :S\longrightarrow S/\mathcal {H}$ is a submersion. The manifold
$\rho :S\longrightarrow S/\mathcal {H}$ is a submersion. The manifold  $S/\mathcal {H}$ then has a unique Poisson structure satisfying the following condition: if
$S/\mathcal {H}$ then has a unique Poisson structure satisfying the following condition: if  $x\in S$,
$x\in S$,  $f,g$ are smooth functions on
$f,g$ are smooth functions on  $S/\mathcal {H}$ defined near
$S/\mathcal {H}$ defined near  $\rho (x)$, and
$\rho (x)$, and  $F,G$ are smooth functions on
$F,G$ are smooth functions on  $X$ defined near
$X$ defined near  $x$ with
$x$ with  $dF(\sigma (TS^{\circ }))=0=dG(\sigma (TS^{\circ }))$, then
Furthermore, the moment map
$dF(\sigma (TS^{\circ }))=0=dG(\sigma (TS^{\circ }))$, then
Furthermore, the moment map \begin{align*} \rho^{*}\{f,g\}_{\mathcal{S}/\mathcal{H}}=\{F,G\}_X\vert_S. \end{align*}
\begin{align*} \rho^{*}\{f,g\}_{\mathcal{S}/\mathcal{H}}=\{F,G\}_X\vert_S. \end{align*} $\mu :M\longrightarrow X$ descends to a Poisson map
$\mu :M\longrightarrow X$ descends to a Poisson map  $M\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S,\mathcal {H}}}\mathcal {G}\longrightarrow S/\mathcal {H}$.
$M\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S,\mathcal {H}}}\mathcal {G}\longrightarrow S/\mathcal {H}$.
This result appears in the main text as Theorems 2.14, 2.20, and 2.24.
Let us suppose that ![]() $S=\{x\}$ is a singleton and that
$S=\{x\}$ is a singleton and that ![]() $\mathcal {H}$ is the isotropy group at
$\mathcal {H}$ is the isotropy group at ![]() $x$. In this case,
$x$. In this case, ![]() $M\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S,\mathcal {H}}}\mathcal {G}$ is precisely the Mikami–Weinstein reduction of
$M\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S,\mathcal {H}}}\mathcal {G}$ is precisely the Mikami–Weinstein reduction of ![]() $M$ at level
$M$ at level ![]() $x$ (see [Reference Mikami and WeinsteinMW88]). In other words, Mikami–Weinstein reduction is a special case of Theorem A. The same is therefore true of Marsden–Weinstein–Meyer reduction, as it is a special case of Mikami–Weinstein reduction.
$x$ (see [Reference Mikami and WeinsteinMW88]). In other words, Mikami–Weinstein reduction is a special case of Theorem A. The same is therefore true of Marsden–Weinstein–Meyer reduction, as it is a special case of Mikami–Weinstein reduction.
It is also illuminating to apply Theorem A in the case of a Poisson transversal ![]() $S\subseteq X$. The trivial groupoid
$S\subseteq X$. The trivial groupoid ![]() $\mathcal {H}\rightrightarrows S$ is then a stabilizer subgroupoid of
$\mathcal {H}\rightrightarrows S$ is then a stabilizer subgroupoid of ![]() $S$ in
$S$ in ![]() $\mathcal {G}$, and one obtains the symplectic submanifold
$\mathcal {G}$, and one obtains the symplectic submanifold ![]() $M\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S,\mathcal {H}}}\mathcal {G}=\mu ^{-1}(S)\subseteq M$.
$M\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S,\mathcal {H}}}\mathcal {G}=\mu ^{-1}(S)\subseteq M$.
1.2.2 The complex analytic and algebraic categories
Theorem A and its consequences have natural counterparts in the category of complex analytic spaces. To this end, call a complex analytic space ![]() $(X,\mathcal {O}_X)$ Poisson if
$(X,\mathcal {O}_X)$ Poisson if ![]() $\mathcal {O}_X$ is a sheaf of complex Poisson algebras. Now assume that
$\mathcal {O}_X$ is a sheaf of complex Poisson algebras. Now assume that ![]() $X$ is a holomorphic Poisson manifold and denote its Poisson bivector field by
$X$ is a holomorphic Poisson manifold and denote its Poisson bivector field by ![]() $\sigma :T^{*}X\longrightarrow TX$. We call a complex submanifold
$\sigma :T^{*}X\longrightarrow TX$. We call a complex submanifold ![]() $S\subseteq X$ a pre-Poisson complex submanifold if
$S\subseteq X$ a pre-Poisson complex submanifold if ![]() $\sigma ^{-1}(TS)\cap TS^{\circ }$ has constant rank over
$\sigma ^{-1}(TS)\cap TS^{\circ }$ has constant rank over ![]() $S$. The base space of a holomorphic symplectic groupoid
$S$. The base space of a holomorphic symplectic groupoid ![]() $\mathcal {G}\rightrightarrows X$ is a holomorphic Poisson manifold, in which context we may consider a pre-Poisson complex submanifold
$\mathcal {G}\rightrightarrows X$ is a holomorphic Poisson manifold, in which context we may consider a pre-Poisson complex submanifold ![]() $S\subseteq X$. In analogy with § 1.2.1, we may define what it means for
$S\subseteq X$. In analogy with § 1.2.1, we may define what it means for ![]() $\mathcal {H}\rightrightarrows S$ to be a holomorphic stabilizer subgroupoid of
$\mathcal {H}\rightrightarrows S$ to be a holomorphic stabilizer subgroupoid of ![]() $S$. Hamiltonian actions are also defined analogously, i.e. one has an analogous notion of
$S$. Hamiltonian actions are also defined analogously, i.e. one has an analogous notion of ![]() $\mathcal {G}\rightrightarrows X$ acting on a holomorphic symplectic manifold
$\mathcal {G}\rightrightarrows X$ acting on a holomorphic symplectic manifold ![]() $M$ in a Hamiltonian fashion with moment map
$M$ in a Hamiltonian fashion with moment map ![]() $\mu :M\longrightarrow X$. Let us assume that
$\mu :M\longrightarrow X$. Let us assume that ![]() $N:= \mu ^{-1}(S)$ is reduced. Let us also consider a complex analytic quotient
$N:= \mu ^{-1}(S)$ is reduced. Let us also consider a complex analytic quotient ![]() $\pi :N\longrightarrow Q$ of
$\pi :N\longrightarrow Q$ of ![]() $N$ by
$N$ by ![]() $\mathcal {H}$; by this, we mean that
$\mathcal {H}$; by this, we mean that ![]() $Q$ is a complex analytic space, that
$Q$ is a complex analytic space, that ![]() $\pi$ is holomorphic, and that the canonical map
$\pi$ is holomorphic, and that the canonical map ![]() $\mathcal {O}_{Q}\longrightarrow (\pi _*\mathcal {O}_N)^{\mathcal {H}}$ is an isomorphism. We refer to
$\mathcal {O}_{Q}\longrightarrow (\pi _*\mathcal {O}_N)^{\mathcal {H}}$ is an isomorphism. We refer to ![]() $Q$ as the symplectic reduction of
$Q$ as the symplectic reduction of ![]() $M$ by
$M$ by ![]() $\mathcal {G}$ along
$\mathcal {G}$ along ![]() $S$ with respect to
$S$ with respect to ![]() $\mathcal {H}$ and
$\mathcal {H}$ and ![]() $\pi$ and write
$\pi$ and write
These considerations yield the following counterpart of Theorem A.
Theorem B (Complex analytic category)
Let a holomorphic symplectic groupoid ![]() $\mathcal {G}\rightrightarrows X$ act on a holomorphic symplectic manifold
$\mathcal {G}\rightrightarrows X$ act on a holomorphic symplectic manifold ![]() $(M,\omega )$ in a Hamiltonian fashion with moment map
$(M,\omega )$ in a Hamiltonian fashion with moment map ![]() $\mu :M\longrightarrow X$. Suppose that
$\mu :M\longrightarrow X$. Suppose that ![]() $\mathcal {H}\rightrightarrows S$ is a holomorphic stabilizer subgroupoid of a pre-Poisson complex submanifold
$\mathcal {H}\rightrightarrows S$ is a holomorphic stabilizer subgroupoid of a pre-Poisson complex submanifold ![]() $S\subseteq X$ and that
$S\subseteq X$ and that ![]() $N:= \mu ^{-1}(S)$ is reduced. Let us also suppose that
$N:= \mu ^{-1}(S)$ is reduced. Let us also suppose that ![]() $\pi :N\longrightarrow Q$ is a complex analytic quotient of
$\pi :N\longrightarrow Q$ is a complex analytic quotient of ![]() $N$ by
$N$ by ![]() $\mathcal {H}$.
$\mathcal {H}$.
(i) If
 $p\in N$ and
$p\in N$ and  $f\in \mathcal {O}_{Q,\pi (p)}$, then there exists
$f\in \mathcal {O}_{Q,\pi (p)}$, then there exists  $F\in \mathcal {O}_{M,p}$ satisfying
$F\in \mathcal {O}_{M,p}$ satisfying  $\pi ^{*}f=F\vert _N$ and
$\pi ^{*}f=F\vert _N$ and  $dF(TN^{\omega })=0$, where
$dF(TN^{\omega })=0$, where  $TN^{\omega }$ is the annihilator of
$TN^{\omega }$ is the annihilator of  $TN$ with respect to
$TN$ with respect to  $\omega$.
$\omega$.(ii) The complex analytic space
 $Q$ has a unique Poisson structure with the following property: if
$Q$ has a unique Poisson structure with the following property: if  $p\in N$,
$p\in N$,  $f,g\in \mathcal {O}_{Q,\pi (p)}$, and
$f,g\in \mathcal {O}_{Q,\pi (p)}$, and  $F,G\in \mathcal {O}_{M,p}$ satisfy
$F,G\in \mathcal {O}_{M,p}$ satisfy  $\pi ^{*}f=F\vert _N$,
$\pi ^{*}f=F\vert _N$,  $\pi ^{*}g=G\vert _N$, and
$\pi ^{*}g=G\vert _N$, and  $dF(TN^{\omega })=0=dG(TN^{\omega })$, then
$dF(TN^{\omega })=0=dG(TN^{\omega })$, then
 \begin{align*} \pi^{*}\{f,g\}_Q=\{F,G\}_M\vert_N. \end{align*}
\begin{align*} \pi^{*}\{f,g\}_Q=\{F,G\}_M\vert_N. \end{align*}(iii) Assume that there exists
 $p\in N$ such that
$p\in N$ such that  $d\pi _p$ is surjective,
$d\pi _p$ is surjective,  $\pi ^{-1}(\pi (p))$ is an
$\pi ^{-1}(\pi (p))$ is an  $\mathcal {H}$-orbit, and
$\mathcal {H}$-orbit, and  $\pi (p)$ is a smooth point of
$\pi (p)$ is a smooth point of  $Q$. The Poisson structure in part (ii) is then non-degenerate on an open dense subset of the smooth locus of
$Q$. The Poisson structure in part (ii) is then non-degenerate on an open dense subset of the smooth locus of  $Q$ containing
$Q$ containing  $\pi (p)$.
$\pi (p)$.(iv) Suppose that
 $S$ intersects
$S$ intersects  $\mu$ cleanly, and that the topological quotient
$\mu$ cleanly, and that the topological quotient  $Q = N/\mathcal {H}$ has a complex manifold structure such that
$Q = N/\mathcal {H}$ has a complex manifold structure such that  $\pi : N \longrightarrow Q$ is a holomorphic submersion. The Poisson structure on
$\pi : N \longrightarrow Q$ is a holomorphic submersion. The Poisson structure on  $Q$ is then induced by a holomorphic symplectic form
$Q$ is then induced by a holomorphic symplectic form  $\bar {\omega }$ satisfying
where
$\bar {\omega }$ satisfying
where \begin{align*} \pi^{*}\bar{\omega} = i^{*}\omega, \end{align*}
\begin{align*} \pi^{*}\bar{\omega} = i^{*}\omega, \end{align*} $i : N \longrightarrow M$ is the inclusion map.
$i : N \longrightarrow M$ is the inclusion map.(v) If
 $\mathcal {H}$ acts freely on
$\mathcal {H}$ acts freely on  $N$, then
$N$, then  $S$ is transverse to
$S$ is transverse to  $\mu$. The hypotheses of part (iv) are therefore satisfied if
$\mu$. The hypotheses of part (iv) are therefore satisfied if  $\mathcal {H}$ acts freely and properly on
$\mathcal {H}$ acts freely and properly on  $N$.
$N$.(vi) Let
 $\sigma :T^{*}X\longrightarrow TX$ denote the Poisson bivector field on
$\sigma :T^{*}X\longrightarrow TX$ denote the Poisson bivector field on  $X$. If
$X$. If  $\rho : S \longrightarrow R$ is a complex analytic quotient of
$\rho : S \longrightarrow R$ is a complex analytic quotient of  $S$ by
$S$ by  $\mathcal {H}$, then there is a unique holomorphic Poisson structure on
$\mathcal {H}$, then there is a unique holomorphic Poisson structure on  $R$ such that
for all
$R$ such that
for all \begin{align*} \rho^{*}\{f, g\}_R = \{F, G\}_X\vert_S \end{align*}
\begin{align*} \rho^{*}\{f, g\}_R = \{F, G\}_X\vert_S \end{align*} $x \in S$,
$x \in S$,  $f, g \in \mathcal {O}_{R, \rho (x)}$, and
$f, g \in \mathcal {O}_{R, \rho (x)}$, and  $F, G \in \mathcal {O}_{X, x}$ satisfying
$F, G \in \mathcal {O}_{X, x}$ satisfying  $\rho ^{*}f = F\vert _S$,
$\rho ^{*}f = F\vert _S$,  $\rho ^{*}g = G\vert _S$, and
$\rho ^{*}g = G\vert _S$, and  $dF(\sigma (TS^{\circ }))=0=dG(\sigma (TS^{\circ }))$.
$dF(\sigma (TS^{\circ }))=0=dG(\sigma (TS^{\circ }))$.(vii) Assume that the hypothesis of part (vi) holds. If
 $\mu : M \longrightarrow X$ descends to a holomorphic map
$\mu : M \longrightarrow X$ descends to a holomorphic map  $\bar {\mu } : Q \longrightarrow R$, then
$\bar {\mu } : Q \longrightarrow R$, then  $\bar {\mu }$ is Poisson with respect to the Poisson structures in parts (ii) and (vi).
$\bar {\mu }$ is Poisson with respect to the Poisson structures in parts (ii) and (vi).
This result appears in the main text as Theorem 3.10, Propositions 3.14, 3.15, and Theorem 3.16.
Theorem B has incarnations in complex algebraic geometry. The setup is entirely analogous to that outlined in the paragraph preceding Theorem B; one simply replaces each complex analytic notion with its algebro-geometric counterpart, e.g. holomorphic symplectic groupoids with algebraic symplectic groupoids, holomorphic Poisson manifolds with smooth Poisson varieties, and complex analytic quotients with algebraic quotients.Footnote 2 The algebro-geometric definition of ![]() $M\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S,\mathcal {H},\pi }}\mathcal {G}$ is then analogous to that given in the complex analytic setting.
$M\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S,\mathcal {H},\pi }}\mathcal {G}$ is then analogous to that given in the complex analytic setting.
Theorem C (Complex algebraic category)
Let an algebraic symplectic groupoid ![]() $\mathcal {G}\rightrightarrows X$ act on a symplectic variety
$\mathcal {G}\rightrightarrows X$ act on a symplectic variety ![]() $(M,\omega )$ in a Hamiltonian fashion with moment map
$(M,\omega )$ in a Hamiltonian fashion with moment map ![]() $\mu :M\longrightarrow X$. Suppose that
$\mu :M\longrightarrow X$. Suppose that ![]() $\mathcal {H}\rightrightarrows S$ is a stabilizer subgroupoid of a pre-Poisson subvariety
$\mathcal {H}\rightrightarrows S$ is a stabilizer subgroupoid of a pre-Poisson subvariety ![]() $S\subseteq X$ and that
$S\subseteq X$ and that ![]() $N:= \mu ^{-1}(S)$ is reduced. Suppose also that
$N:= \mu ^{-1}(S)$ is reduced. Suppose also that ![]() $\pi :N\longrightarrow Q$ is an algebraic quotient of
$\pi :N\longrightarrow Q$ is an algebraic quotient of ![]() $N$ by
$N$ by ![]() $\mathcal {H}$. Let
$\mathcal {H}$. Let ![]() $\mathcal {O}_M^{{\rm an}}$ denote the structure sheaf of
$\mathcal {O}_M^{{\rm an}}$ denote the structure sheaf of ![]() $M$ as a complex analytic space.
$M$ as a complex analytic space.
(i) If
 $p\in N$ and
$p\in N$ and  $f\in \mathcal {O}_{Q,\pi (p)}$, then there exists
$f\in \mathcal {O}_{Q,\pi (p)}$, then there exists  $F$ in
$F$ in  $\mathcal {O}_{M,p}^{{\rm an}}$ satisfying
$\mathcal {O}_{M,p}^{{\rm an}}$ satisfying  $\pi ^{*}f=F\vert _N$ and
$\pi ^{*}f=F\vert _N$ and  ${dF(TN^{\omega })=0}$.
${dF(TN^{\omega })=0}$.(ii) The variety
 $Q$ has a unique algebraic Poisson structure with the following property: if
$Q$ has a unique algebraic Poisson structure with the following property: if  $p\in N$,
$p\in N$,  $f,g\in \mathcal {O}_{Q,\pi (p)}$, and
$f,g\in \mathcal {O}_{Q,\pi (p)}$, and  $F,G\in \mathcal {O}_{M,p}^{{\rm an}}$ satisfy
$F,G\in \mathcal {O}_{M,p}^{{\rm an}}$ satisfy  $\pi ^{*}f=F\vert _N$,
$\pi ^{*}f=F\vert _N$,  $\pi ^{*}g=G\vert _N$, and
$\pi ^{*}g=G\vert _N$, and  $dF(TN^{\omega })=0=dG(TN^{\omega })$, then
$dF(TN^{\omega })=0=dG(TN^{\omega })$, then
 \begin{align*} \pi^{*}\{f,g\}_Q=\{F,G\}_M\vert_N. \end{align*}
\begin{align*} \pi^{*}\{f,g\}_Q=\{F,G\}_M\vert_N. \end{align*}(iii) Assume that there exists
 $p \in N$ such that
$p \in N$ such that  $d\pi _p$ is surjective,
$d\pi _p$ is surjective,  $\pi ^{-1}(\pi (p))$ is an
$\pi ^{-1}(\pi (p))$ is an  $\mathcal {H}$-orbit, and
$\mathcal {H}$-orbit, and  $\pi (p)$ is a smooth point of
$\pi (p)$ is a smooth point of  $Q$. The Poisson structure in part (ii) is then non-degenerate on a Zariski-open subset of the smooth locus of
$Q$. The Poisson structure in part (ii) is then non-degenerate on a Zariski-open subset of the smooth locus of  $Q$ containing
$Q$ containing  $\pi (p)$.
$\pi (p)$.
1.2.3 Symplectic reduction by a Lie group along a submanifold
Our results have implications for classical Hamiltonian ![]() $G$-spaces in both the smooth and complex analytic categories, where
$G$-spaces in both the smooth and complex analytic categories, where ![]() $G$ is any real or complex Lie group with Lie algebra
$G$ is any real or complex Lie group with Lie algebra ![]() $\mathfrak {g}$. We develop the implications for smooth Hamiltonian
$\mathfrak {g}$. We develop the implications for smooth Hamiltonian ![]() $G$-spaces in parallel with those for holomorphic Hamiltonian
$G$-spaces in parallel with those for holomorphic Hamiltonian ![]() $G$-spaces, allowing context to resolve any ambiguities that this may create.
$G$-spaces, allowing context to resolve any ambiguities that this may create.
Recall the identification of Hamiltonian ![]() $G$-spaces with Hamiltonian spaces for the cotangent groupoid
$G$-spaces with Hamiltonian spaces for the cotangent groupoid ![]() $T^{*}G\rightrightarrows \mathfrak {g}^{*}$ described in [Reference Mikami and WeinsteinMW88] and mentioned in § 1.1. This gives rise to the notation
$T^{*}G\rightrightarrows \mathfrak {g}^{*}$ described in [Reference Mikami and WeinsteinMW88] and mentioned in § 1.1. This gives rise to the notation
for the reduction of a Hamiltonian ![]() $G$-space
$G$-space ![]() $M$ along a pre-Poisson submanifold
$M$ along a pre-Poisson submanifold ![]() $S\subseteq \mathfrak {g}^{*}$ with respect to a stabilizer subgroupoid
$S\subseteq \mathfrak {g}^{*}$ with respect to a stabilizer subgroupoid ![]() $\mathcal {H}\rightrightarrows S$ in
$\mathcal {H}\rightrightarrows S$ in ![]() $T^{*}G$. As per (1.3) and the discussion preceding it, we may write
$T^{*}G$. As per (1.3) and the discussion preceding it, we may write
On the other hand, we call the pair ![]() $(S,\mathcal {H})$ a clean reduction datum if it satisfies the hypotheses of Theorems A(i) or B(iv). Note that
$(S,\mathcal {H})$ a clean reduction datum if it satisfies the hypotheses of Theorems A(i) or B(iv). Note that ![]() $M\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S,\mathcal {H}}}G$ is a symplectic manifold in this case.
$M\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S,\mathcal {H}}}G$ is a symplectic manifold in this case.
One may specialize this discussion to the Hamiltonian ![]() $G$-space
$G$-space ![]() $M=T^{*}G$, where
$M=T^{*}G$, where ![]() $G$ acts on
$G$ acts on ![]() $T^{*}G$ by right translations. Let us begin by considering
$T^{*}G$ by right translations. Let us begin by considering
Note that ![]() $\mathfrak {M}_{G,S,\mathcal {H}}$ is a symplectic manifold if
$\mathfrak {M}_{G,S,\mathcal {H}}$ is a symplectic manifold if ![]() $(S,\mathcal {H})$ is a clean reduction datum for the right translation action of
$(S,\mathcal {H})$ is a clean reduction datum for the right translation action of ![]() $G$ on
$G$ on ![]() $T^{*}G$. In this case, the left translation action descends to a Hamiltonian
$T^{*}G$. In this case, the left translation action descends to a Hamiltonian ![]() $G$-action on
$G$-action on ![]() $\mathfrak {M}_{G,S,\mathcal {H}}$, i.e.
$\mathfrak {M}_{G,S,\mathcal {H}}$, i.e. ![]() $\mathfrak {M}_{G,S,\mathcal {H}}$ is a Hamiltonian
$\mathfrak {M}_{G,S,\mathcal {H}}$ is a Hamiltonian ![]() $G$-space. Part (i) of the following result justifies our calling
$G$-space. Part (i) of the following result justifies our calling ![]() $\mathfrak {M}_{G,S,\mathcal {H}}$ the universal reduced space associated to
$\mathfrak {M}_{G,S,\mathcal {H}}$ the universal reduced space associated to ![]() $(G,S,\mathcal {H})$.
$(G,S,\mathcal {H})$.
Theorem D (Reduction by a Lie group)
Let ![]() $S\subseteq \mathfrak {g}^{*}$ be a pre-Poisson submanifold.
$S\subseteq \mathfrak {g}^{*}$ be a pre-Poisson submanifold.
(i) Suppose that
 $(S,\mathcal {H})$ is a clean reduction datum for both a Hamiltonian
$(S,\mathcal {H})$ is a clean reduction datum for both a Hamiltonian  $G$-space
$G$-space  $M$ and the right translation action of
$M$ and the right translation action of  $G$ on
$G$ on  $T^{*}G$. We then have a canonical symplectomorphism
where
$T^{*}G$. We then have a canonical symplectomorphism
where \begin{align*} M \mkern-4mu\mathbin{/\mkern-5mu/}_{\mkern-4mu{S, \mathcal{H}}} G \cong (M \times \mathfrak{M}_{G, S, \mathcal{H}}^{-}) \mkern-4mu\mathbin{/\mkern-5mu/}_{\mkern-4mu{0}} G, \end{align*}
\begin{align*} M \mkern-4mu\mathbin{/\mkern-5mu/}_{\mkern-4mu{S, \mathcal{H}}} G \cong (M \times \mathfrak{M}_{G, S, \mathcal{H}}^{-}) \mkern-4mu\mathbin{/\mkern-5mu/}_{\mkern-4mu{0}} G, \end{align*} $\mathfrak {M}_{G, S, \mathcal {H}}^{-}$ is
$\mathfrak {M}_{G, S, \mathcal {H}}^{-}$ is  $\mathfrak {M}_{G, S, \mathcal {H}}$ with the negated symplectic form,
$\mathfrak {M}_{G, S, \mathcal {H}}$ with the negated symplectic form,  $G$ acts diagonally on
$G$ acts diagonally on  $M \times \mathfrak {M}_{G, S, \mathcal {H}}^{-}$, and
$M \times \mathfrak {M}_{G, S, \mathcal {H}}^{-}$, and  $\,\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{0}}$ denotes Marsden–Weinstein–Meyer reduction at level
$\,\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{0}}$ denotes Marsden–Weinstein–Meyer reduction at level  $0$.
$0$.(ii) Suppose that the Lie subalgebroid
 $L_S := \sigma ^{-1}(TS) \cap TS^{\circ } \subseteq T^{*}\mathfrak {g}^{*}$ is contained in the kernel of the Kirillov–Kostant–Souriau Poisson structure
$L_S := \sigma ^{-1}(TS) \cap TS^{\circ } \subseteq T^{*}\mathfrak {g}^{*}$ is contained in the kernel of the Kirillov–Kostant–Souriau Poisson structure  $\sigma :T^{*}\mathfrak {g}^{*}\longrightarrow T\mathfrak {g}^{*}$. The subspace
is then a Lie subalgebra of
$\sigma :T^{*}\mathfrak {g}^{*}\longrightarrow T\mathfrak {g}^{*}$. The subspace
is then a Lie subalgebra of \begin{align*} \mathfrak{h}_{\xi}:= (T_{\xi}S)^{\circ}\cap\mathfrak{g}_{\xi} \end{align*}
\begin{align*} \mathfrak{h}_{\xi}:= (T_{\xi}S)^{\circ}\cap\mathfrak{g}_{\xi} \end{align*} $\mathfrak {g}$ for all
$\mathfrak {g}$ for all  $\xi \in S$, where
$\xi \in S$, where  $(T_{\xi }S)^{\circ }\subseteq \mathfrak {g}$ is the annihilator of
$(T_{\xi }S)^{\circ }\subseteq \mathfrak {g}$ is the annihilator of  $T_{\xi }S\subseteq \mathfrak {g}^{*}$ and
$T_{\xi }S\subseteq \mathfrak {g}^{*}$ and  $\mathfrak {g}_{\xi }\subseteq \mathfrak {g}$ is the centralizer of
$\mathfrak {g}_{\xi }\subseteq \mathfrak {g}$ is the centralizer of  $\xi$. Furthermore, we have
$\xi$. Furthermore, we have
 \begin{align*} L_S=\{(x,\xi)\in \mathfrak{g}\times S:x\in\mathfrak{h}_{\xi}\}. \end{align*}
\begin{align*} L_S=\{(x,\xi)\in \mathfrak{g}\times S:x\in\mathfrak{h}_{\xi}\}. \end{align*}(iii) Retain the hypothesis of part (ii). Let
 $H_{\xi }\subseteq G$ be the connected Lie subgroup with Lie algebra
$H_{\xi }\subseteq G$ be the connected Lie subgroup with Lie algebra  $\mathfrak {h}_{\xi }$ for all
$\mathfrak {h}_{\xi }$ for all  $\xi \in S$, and suppose that
is closed in
$\xi \in S$, and suppose that
is closed in \begin{align*} \mathcal{H}:=\{(g,\xi)\in G\times S:g\in H_{\xi}\} \end{align*}
\begin{align*} \mathcal{H}:=\{(g,\xi)\in G\times S:g\in H_{\xi}\} \end{align*} $G\times S$. The subset
$G\times S$. The subset  $\mathcal {H}$ is then a stabilizer subgroupoid of
$\mathcal {H}$ is then a stabilizer subgroupoid of  $S$ in
$S$ in  $T^{*}G\rightrightarrows \mathfrak {g}^{*}$ if one uses the left trivialization to identify
$T^{*}G\rightrightarrows \mathfrak {g}^{*}$ if one uses the left trivialization to identify  $T^{*}G$ with
$T^{*}G$ with  $G\times \mathfrak {g}^{*}$.
$G\times \mathfrak {g}^{*}$.(iv) Suppose that
 $S$ is a
$S$ is a  $G$-invariant submanifold of
$G$-invariant submanifold of  $\mathfrak {g}^{*}$. The hypothesis of part (ii) is then satisfied. Let us also assume that the hypotheses of part (iii) are satisfied. Then
$\mathfrak {g}^{*}$. The hypothesis of part (ii) is then satisfied. Let us also assume that the hypotheses of part (iii) are satisfied. Then  $(S,\mathcal {H})$ is a clean reduction datum for the right translation action of
$(S,\mathcal {H})$ is a clean reduction datum for the right translation action of  $G$ on
$G$ on  $T^{*}G$, and the symplectic manifold
$T^{*}G$, and the symplectic manifold  $\mathfrak {M}_{G,S}$ inherits the structure of a symplectic groupoid integrating
$\mathfrak {M}_{G,S}$ inherits the structure of a symplectic groupoid integrating  $S$.
$S$.
Theorem D appears in the main text as Proposition 4.10 and Theorems 4.11, 4.17, and 4.21.
We proceed to obtain the following specific examples of universal reduced spaces.
Theorem E (Specific examples of universal reduced spaces)
Let ![]() $G$ be a connected complex semisimple Lie group with Lie algebra
$G$ be a connected complex semisimple Lie group with Lie algebra ![]() $\mathfrak {g}$.
$\mathfrak {g}$.
(i) If
 $G$ is of adjoint type,
$G$ is of adjoint type,  $\mathcal {S}\subseteq \mathfrak {g}^{*}$ is a principal Slodowy slice, and
$\mathcal {S}\subseteq \mathfrak {g}^{*}$ is a principal Slodowy slice, and  $\Delta _n\mathcal {S}\subseteq (\mathfrak {g}^{*})^{n}$ is the diagonally embedded copy of
$\Delta _n\mathcal {S}\subseteq (\mathfrak {g}^{*})^{n}$ is the diagonally embedded copy of  $\mathcal {S}$, then
$\mathcal {S}$, then  $\mathfrak {M}_{G^{n},\Delta _n\mathcal {S}}$ is the
$\mathfrak {M}_{G^{n},\Delta _n\mathcal {S}}$ is the  $n$th open Moore–Tachikawa variety. Its affinization is the
$n$th open Moore–Tachikawa variety. Its affinization is the  $n$th Moore–Tachikawa variety constructed by Ginzburg–Kazhdan, and the Poisson structure on this variety can be recovered from Theorem C.
$n$th Moore–Tachikawa variety constructed by Ginzburg–Kazhdan, and the Poisson structure on this variety can be recovered from Theorem C.(ii) If
 $(\mathfrak {g}^{*}_{\mathrm {irr}})^{\circ }$ is the set of subregular semisimple elements in
$(\mathfrak {g}^{*}_{\mathrm {irr}})^{\circ }$ is the set of subregular semisimple elements in  $\mathfrak {g}^{*}$, then
where
$\mathfrak {g}^{*}$, then
where \begin{align*} \mathfrak{M}_{G,(\mathfrak{g}^{*}_{\mathrm{irr}})^{\circ}}=\bigsqcup_{\xi\in (\mathfrak{g}^{*}_{\mathrm{irr}})^{\circ}}G/[G_{\xi},G_{\xi}], \end{align*}
\begin{align*} \mathfrak{M}_{G,(\mathfrak{g}^{*}_{\mathrm{irr}})^{\circ}}=\bigsqcup_{\xi\in (\mathfrak{g}^{*}_{\mathrm{irr}})^{\circ}}G/[G_{\xi},G_{\xi}], \end{align*} $G_{\xi }$ is the
$G_{\xi }$ is the  $G$-stabilizer of
$G$-stabilizer of  $\xi \in \mathfrak {g}^{*}$. Furthermore, this space has the structure of a holomorphic symplectic groupoid integrating
$\xi \in \mathfrak {g}^{*}$. Furthermore, this space has the structure of a holomorphic symplectic groupoid integrating  $(\mathfrak {g}^{*}_{\mathrm {irr}})^{\circ }$. Its symplectic form, Hamiltonian
$(\mathfrak {g}^{*}_{\mathrm {irr}})^{\circ }$. Its symplectic form, Hamiltonian  $G$-action, and groupoid structure are described in Example 4.36.
$G$-action, and groupoid structure are described in Example 4.36.
Theorem E appears in the main text as Example 4.36 and Theorem 5.10.
A few brief comments are warranted. We first note that the stabilizer subgroupoid used to construct ![]() $\mathfrak {M}_{G^{n},\Delta _n\mathcal {S}}$ is a genuine group scheme, i.e. a group scheme whose fibers are not all isomorphic to one another. This contrasts with the more familiar construction of reduced spaces as quotients by Lie group actions. The Ginzburg–Kazhdan construction of Moore–Tachikawa varieties thereby inspired much of the setup in this paper. In particular, this construction was the main motivation for our work.
$\mathfrak {M}_{G^{n},\Delta _n\mathcal {S}}$ is a genuine group scheme, i.e. a group scheme whose fibers are not all isomorphic to one another. This contrasts with the more familiar construction of reduced spaces as quotients by Lie group actions. The Ginzburg–Kazhdan construction of Moore–Tachikawa varieties thereby inspired much of the setup in this paper. In particular, this construction was the main motivation for our work.
Our second comment is that Theorem E(ii) holds in greater generality; one can reduce along any decomposition class ![]() $\mathcal {D}\subseteq \mathfrak {g}^{*}$ (see [Reference Borho and KraftBK79]) and obtain an explicit description of the Hamiltonian
$\mathcal {D}\subseteq \mathfrak {g}^{*}$ (see [Reference Borho and KraftBK79]) and obtain an explicit description of the Hamiltonian ![]() $G$-space
$G$-space ![]() $\mathfrak {M}_{G,\mathcal {D}}$. The Hamiltonian
$\mathfrak {M}_{G,\mathcal {D}}$. The Hamiltonian ![]() $G$-spaces
$G$-spaces ![]() $\mathfrak {M}_{G,\mathcal {D}}$ do not seem to appear in the literature.
$\mathfrak {M}_{G,\mathcal {D}}$ do not seem to appear in the literature.
1.2.4 Examples of symplectic reduction along a submanifold
In addition to Marsden– Weinstein–Meyer reduction, Mikami–Weinstein reduction, and the pre-images of Poisson transversals under moment maps, we realize each of the following as special cases of symplectic reduction along a submanifold. Retain the notation used in § 1.2.3 and identify ![]() $T^{*}G$ with
$T^{*}G$ with ![]() $G\times \mathfrak {g}^{*}$ via the left trivialization as appropriate. Write
$G\times \mathfrak {g}^{*}$ via the left trivialization as appropriate. Write ![]() $G_{\xi }$ for the
$G_{\xi }$ for the ![]() $G$-stabilizer of
$G$-stabilizer of ![]() $\xi \in \mathfrak {g}^{*}$.
$\xi \in \mathfrak {g}^{*}$.
Theorem F (General examples)
Let ![]() $G$ be a Lie group with Lie algebra
$G$ be a Lie group with Lie algebra ![]() $\mathfrak {g}$. Suppose that
$\mathfrak {g}$. Suppose that ![]() $G$ acts on a symplectic manifold
$G$ acts on a symplectic manifold ![]() $M$ in a Hamiltonian fashion and with moment map
$M$ in a Hamiltonian fashion and with moment map ![]() $\mu :M\longrightarrow \mathfrak {g}^{*}$.
$\mu :M\longrightarrow \mathfrak {g}^{*}$.
(i) If
 $\mathcal {O}\subseteq \mathfrak {g}^{*}$ is a coadjoint orbit,
$\mathcal {O}\subseteq \mathfrak {g}^{*}$ is a coadjoint orbit,  $\mathcal {H}=\{(g,\xi )\in G\times \mathcal {O}:g\in G_{\xi }\}$,
$\mathcal {H}=\{(g,\xi )\in G\times \mathcal {O}:g\in G_{\xi }\}$,  $(\mathcal {O},\mathcal {H})$ is a clean reduction datum, and
$(\mathcal {O},\mathcal {H})$ is a clean reduction datum, and  $\mathcal {O}^{-}$ is
$\mathcal {O}^{-}$ is  $\mathcal {O}$ with the negated symplectic form, then
$\mathcal {O}$ with the negated symplectic form, then  $M\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{\mathcal {O},\mathcal {H}}}G=\mu ^{-1}(\mathcal {O})/G\times \mathcal {O}^{-}$.
$M\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{\mathcal {O},\mathcal {H}}}G=\mu ^{-1}(\mathcal {O})/G\times \mathcal {O}^{-}$.(ii) If
 $G$ is compact and connected and
$G$ is compact and connected and  $\mathfrak {t}_+^{*}\subseteq \mathfrak {g}^{*}$ is a closed fundamental Weyl chamber, then
$\mathfrak {t}_+^{*}\subseteq \mathfrak {g}^{*}$ is a closed fundamental Weyl chamber, then  $M\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{\mathfrak {t}_+^{*}}}G$ is the imploded cross-section of
$M\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{\mathfrak {t}_+^{*}}}G$ is the imploded cross-section of  $M$.
$M$.(iii) If
 $G=T$ is a compact torus and
$G=T$ is a compact torus and  $P\subseteq \mathfrak {g}^{*}=\mathfrak {t}^{*}$ is a polyhedral set, then
$P\subseteq \mathfrak {g}^{*}=\mathfrak {t}^{*}$ is a polyhedral set, then  $M\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{P}}T$ is the symplectic cut of
$M\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{P}}T$ is the symplectic cut of  $M$ with respect to
$M$ with respect to  $P$.
$P$.
Although ![]() $\mathfrak {t}_+^{*}$ and
$\mathfrak {t}_+^{*}$ and ![]() $P$ are not submanifolds, each is stratified into pre-Poisson submanifolds. This allows one to form each of
$P$ are not submanifolds, each is stratified into pre-Poisson submanifolds. This allows one to form each of ![]() $M\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{\mathfrak {t}_+^{*}}}G$ and
$M\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{\mathfrak {t}_+^{*}}}G$ and ![]() $M\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{P}}T$ on a stratum-by-stratum basis. We refer the reader to Remark 2.17 for further details.
$M\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{P}}T$ on a stratum-by-stratum basis. We refer the reader to Remark 2.17 for further details.
Theorem F appears in the main text as Propositions 4.26, 4.29, and 4.32.
1.2.5 Shifted symplectic interpretation
The notion of symplectic reduction along a submanifold can be interpreted as a construction in shifted symplectic geometry [Reference Pantev, Toën, Vaquié and VezzosiPTVV13] similar to that for Marsden–Weinstein–Meyer reduction [Reference Calaque, Anel and CatrenCal20, § 2.1.2] and quasi-Hamiltonian reduction [Reference SafronovSaf16]. More precisely, we obtain it as a derived intersection of two Lagrangian morphisms [Reference Pantev, Toën, Vaquié and VezzosiPTVV13, Theorem 2.9] in the ![]() $1$-shifted symplectic stack
$1$-shifted symplectic stack ![]() $[X/\mathcal {G}]$ associated to a symplectic groupoid
$[X/\mathcal {G}]$ associated to a symplectic groupoid ![]() $\mathcal {G} \rightrightarrows X$. One consequence is that most of the assumptions of Theorem C can be dropped at the expense of obtaining a derived stack
$\mathcal {G} \rightrightarrows X$. One consequence is that most of the assumptions of Theorem C can be dropped at the expense of obtaining a derived stack ![]() $[M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S, \mathcal {H}}} \mathcal {G}]$ endowed with a 0-shifted symplectic structure. This picture also explains the definition of a stabilizer subgroupoid, as shown by part (i) of the following theorem.
$[M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S, \mathcal {H}}} \mathcal {G}]$ endowed with a 0-shifted symplectic structure. This picture also explains the definition of a stabilizer subgroupoid, as shown by part (i) of the following theorem.
Theorem G (Shifted symplectic interpretation)
Let ![]() $\mathcal {G} \rightrightarrows X$ be an algebraic symplectic groupoid.
$\mathcal {G} \rightrightarrows X$ be an algebraic symplectic groupoid.
(i) An algebraic subgroupoid
 $\mathcal {H} \rightrightarrows S$ of
$\mathcal {H} \rightrightarrows S$ of  $\mathcal {G} \rightrightarrows X$ is a stabilizer subgroupoid of a pre-Poisson subvariety if and only if the zero
$\mathcal {G} \rightrightarrows X$ is a stabilizer subgroupoid of a pre-Poisson subvariety if and only if the zero  $2$-form on
$2$-form on  $S$ is a Lagrangian structure on the morphism of quotient stacks
$S$ is a Lagrangian structure on the morphism of quotient stacks  $[S/\mathcal {H}] \longrightarrow [X/\mathcal {G}]$.
$[S/\mathcal {H}] \longrightarrow [X/\mathcal {G}]$.(ii) Suppose that
 $\mathcal {G} \rightrightarrows X$ acts on a symplectic variety
$\mathcal {G} \rightrightarrows X$ acts on a symplectic variety  $M$ in a Hamiltonian fashion with moment map
$M$ in a Hamiltonian fashion with moment map  $\mu : M \longrightarrow X$, and let
$\mu : M \longrightarrow X$, and let  $\mathcal {H} \rightrightarrows S$ be a stabilizer subgroupoid of a pre-Poisson subvariety
$\mathcal {H} \rightrightarrows S$ be a stabilizer subgroupoid of a pre-Poisson subvariety  $S$ in
$S$ in  $\mathcal {G} \rightrightarrows X$. We then have two Lagrangian morphisms
$\mathcal {G} \rightrightarrows X$. We then have two Lagrangian morphisms  $[S/\mathcal {H}] \longrightarrow [X/\mathcal {G}]$ and
$[S/\mathcal {H}] \longrightarrow [X/\mathcal {G}]$ and  $[\mu ] : [M/\mathcal {G}] \longrightarrow [X/\mathcal {G}]$ on the
$[\mu ] : [M/\mathcal {G}] \longrightarrow [X/\mathcal {G}]$ on the  $1$-shifted symplectic stack
$1$-shifted symplectic stack  $[X/\mathcal {G}]$, inducing a
$[X/\mathcal {G}]$, inducing a  $0$-shifted symplectic structure on the derived fiber product
$0$-shifted symplectic structure on the derived fiber product
 \begin{align*} [M\mkern-4mu\mathbin{/\mkern-5mu/}_{\mkern-4mu{S, \mathcal{H}}} \mathcal{G}] := [S/\mathcal{H}] \times_{[X/\mathcal{G}]}^{h} [M/\mathcal{G}]. \end{align*}
\begin{align*} [M\mkern-4mu\mathbin{/\mkern-5mu/}_{\mkern-4mu{S, \mathcal{H}}} \mathcal{G}] := [S/\mathcal{H}] \times_{[X/\mathcal{G}]}^{h} [M/\mathcal{G}]. \end{align*}
This result appears in the main text as Proposition 6.1 and Theorem 6.2.
1.3 Organization
Our paper is organized as follows. Sections 2, 3, 4, 5, and 6 are based around the discussions, proofs, and implications of Theorems A, B, D, C, and G, respectively. Theorem E is divided between §§ 4 and 5, whereas Theorem F appears in § 4. Each of the sections in this paper begins with an outline of its content and structure. Section 6 is followed by a list of recurring notation in our paper.
2. Main construction: smooth version
The present section is devoted to the discussion, proof, and implications of Theorem A. We begin with an overview of the Lie groupoid-theoretic preliminaries in § 2.1. This leads to treatment of pre-Poisson submanifolds and stabilizer subgroupoids in § 2.2. The proofs of parts (i), (ii), and (iii) in Theorem A then appear in §§ 2.3, 2.4, and 2.5, respectively. We conclude with § 2.6, which briefly outlines some special cases of Theorem A.
2.1 Preliminaries
We begin by assembling the concepts and conventions needed to define and study symplectic reduction along a submanifold.
2.1.1 Actions of Lie groupoids
Let ![]() $\mathcal {G} \rightrightarrows X$ be a Lie groupoid. We denote the source and target maps by
$\mathcal {G} \rightrightarrows X$ be a Lie groupoid. We denote the source and target maps by ![]() $\mathsf {s}:\mathcal {G}\longrightarrow X$ and
$\mathsf {s}:\mathcal {G}\longrightarrow X$ and ![]() $\mathsf {t}:\mathcal {G}\longrightarrow X$, respectively. Our convention is that, given
$\mathsf {t}:\mathcal {G}\longrightarrow X$, respectively. Our convention is that, given ![]() $g, h \in \mathcal {G}$, the product
$g, h \in \mathcal {G}$, the product ![]() $gh$ is defined if and only if
$gh$ is defined if and only if ![]() $\mathsf {t}(g) = \mathsf {s}(h)$. The base
$\mathsf {t}(g) = \mathsf {s}(h)$. The base ![]() $X$ is identified as a submanifold of
$X$ is identified as a submanifold of ![]() $\mathcal {G}$ via the identity bisection
$\mathcal {G}$ via the identity bisection ![]() $1 : X \hookrightarrow \mathcal {G}$. We say that
$1 : X \hookrightarrow \mathcal {G}$. We say that ![]() $\mathcal {G} \rightrightarrows X$ is an ssc Lie groupoid if every fiber of
$\mathcal {G} \rightrightarrows X$ is an ssc Lie groupoid if every fiber of ![]() $\mathsf {s}$ is connected and simply-connected. The Lie algebroid of
$\mathsf {s}$ is connected and simply-connected. The Lie algebroid of ![]() $\mathcal {G} \rightrightarrows X$ shall be denoted
$\mathcal {G} \rightrightarrows X$ shall be denoted ![]() $\operatorname {Lie}(\mathcal {G})$ and realized as the vector bundle
$\operatorname {Lie}(\mathcal {G})$ and realized as the vector bundle ![]() $(\ker d\mathsf {t})\vert _X \longrightarrow X$ with anchor map
$(\ker d\mathsf {t})\vert _X \longrightarrow X$ with anchor map ![]() $d\mathsf {s} : (\ker d\mathsf {t})\vert _X \longrightarrow TX$.
$d\mathsf {s} : (\ker d\mathsf {t})\vert _X \longrightarrow TX$.
Now consider a smooth manifold ![]() $M$, a smooth map
$M$, a smooth map ![]() $\mu :M\longrightarrow X$, and the fibered product
$\mu :M\longrightarrow X$, and the fibered product
Recall that an action of ![]() $\mathcal {G} \rightrightarrows X$ on
$\mathcal {G} \rightrightarrows X$ on ![]() $M$ with moment map
$M$ with moment map ![]() $\mu$ is a smooth map
$\mu$ is a smooth map
such that ![]() $\mu (g \cdot p) = \mathsf {s}(g)$,
$\mu (g \cdot p) = \mathsf {s}(g)$, ![]() $(g \cdot h) \cdot p = g \cdot (h \cdot p)$, and
$(g \cdot h) \cdot p = g \cdot (h \cdot p)$, and ![]() $1_{\mu (p)} \cdot p = p$ for all
$1_{\mu (p)} \cdot p = p$ for all ![]() $p \in M$ and
$p \in M$ and ![]() $g, h \in \mathcal {G}$ for which these expressions are defined. The
$g, h \in \mathcal {G}$ for which these expressions are defined. The ![]() $\mathcal {G}$-orbit of a point
$\mathcal {G}$-orbit of a point ![]() $p \in M$ is the set
$p \in M$ is the set
an immersed submanifold of ![]() $M$. The quotient of
$M$. The quotient of ![]() $M$ by
$M$ by ![]() $\mathcal {G}$, denoted
$\mathcal {G}$, denoted ![]() $M / \mathcal {G}$, is the space of orbits with the quotient topology. We say that the action is free if
$M / \mathcal {G}$, is the space of orbits with the quotient topology. We say that the action is free if ![]() $g \cdot p = p$ for
$g \cdot p = p$ for ![]() $(g, p) \in \mathcal {G}_{\mathsf {t}}{\times }_\mu M$ implies
$(g, p) \in \mathcal {G}_{\mathsf {t}}{\times }_\mu M$ implies ![]() $g = 1_{\mu (p)}$, and proper if the map
$g = 1_{\mu (p)}$, and proper if the map
is proper. As for Lie group actions, if the action is free and proper, or more generally the image of (2.1) is a closed embedded submanifold, then the quotient ![]() $M / \mathcal {G}$ is a topological manifold with a unique smooth structure such that the quotient map
$M / \mathcal {G}$ is a topological manifold with a unique smooth structure such that the quotient map ![]() $M \longrightarrow M / \mathcal {G}$ is a smooth submersion [Reference MackenzieMac05, Theorem 1.6.20].
$M \longrightarrow M / \mathcal {G}$ is a smooth submersion [Reference MackenzieMac05, Theorem 1.6.20].
2.1.2 Hamiltonian systems
Let us recall the notion of a Hamiltonian action of a symplectic groupoid on a symplectic manifold, following Mikami–Weinstein [Reference Mikami and WeinsteinMW88].
A Poisson bivector field on a smooth manifold ![]() $P$ is a bundle map
$P$ is a bundle map ![]() $\sigma : T^{*}P \longrightarrow TP$ such that the bilinear map
$\sigma : T^{*}P \longrightarrow TP$ such that the bilinear map ![]() $\{f, g\} := \sigma (df)g$ on smooth functions
$\{f, g\} := \sigma (df)g$ on smooth functions ![]() $f, g \in C^{\infty }(P)$ is a Lie bracket. In this case, we call the pair
$f, g \in C^{\infty }(P)$ is a Lie bracket. In this case, we call the pair ![]() $(P, \sigma )$ a Poisson manifold. For a smooth function
$(P, \sigma )$ a Poisson manifold. For a smooth function ![]() $f$ on
$f$ on ![]() $P$, we denote by
$P$, we denote by ![]() $X_f$ the Hamiltonian vector field
$X_f$ the Hamiltonian vector field ![]() $X_f := \sigma (df)$. We denote by
$X_f := \sigma (df)$. We denote by ![]() $P^{-}$ the Poisson manifold with the opposite Poisson structure
$P^{-}$ the Poisson manifold with the opposite Poisson structure ![]() $-\sigma$. We say that a submanifold
$-\sigma$. We say that a submanifold ![]() $Q \subseteq P$ is coisotropic if
$Q \subseteq P$ is coisotropic if ![]() $\sigma (TQ^{\circ }) \subseteq TQ$, where
$\sigma (TQ^{\circ }) \subseteq TQ$, where ![]() $TQ^{\circ }$ is the annihilator of
$TQ^{\circ }$ is the annihilator of ![]() $TQ$ in
$TQ$ in ![]() $T^{*}P$.
$T^{*}P$.
A symplectic groupoid [Reference Costé, Dazord and WeinsteinCDW87, Reference WeinsteinWei87] is a Lie groupoid ![]() $\mathcal {G}\rightrightarrows X$ together with a symplectic form
$\mathcal {G}\rightrightarrows X$ together with a symplectic form ![]() $\Omega$ on
$\Omega$ on ![]() $\mathcal {G}$, such that the graph
$\mathcal {G}$, such that the graph
of multiplication is Lagrangian in ![]() $\mathcal {G} \times \mathcal {G} \times \mathcal {G}^{-}$. In this case, there is a canonical vector bundle isomorphism
$\mathcal {G} \times \mathcal {G} \times \mathcal {G}^{-}$. In this case, there is a canonical vector bundle isomorphism ![]() $\operatorname {Lie}(\mathcal {G}) \cong T^{*}X$ given by
$\operatorname {Lie}(\mathcal {G}) \cong T^{*}X$ given by
for all ![]() $x \in X$, where
$x \in X$, where ![]() $\Omega$ is viewed as a bundle map
$\Omega$ is viewed as a bundle map ![]() $T\mathcal {G} \longrightarrow T^{*}\mathcal {G}$. The anchor map
$T\mathcal {G} \longrightarrow T^{*}\mathcal {G}$. The anchor map ![]() $\sigma : \operatorname {Lie}(\mathcal {G}) \cong T^{*}X \longrightarrow TX$ is then a Poisson bivector field on
$\sigma : \operatorname {Lie}(\mathcal {G}) \cong T^{*}X \longrightarrow TX$ is then a Poisson bivector field on ![]() $X$ such that the source and target maps are Poisson and anti-Poisson, respectively.
$X$ such that the source and target maps are Poisson and anti-Poisson, respectively.
Definition 2.1 (Mikami–Weinstein [Reference Mikami and WeinsteinMW88])
An action of a symplectic groupoid ![]() $\mathcal {G}\rightrightarrows X$ on a Poisson manifold
$\mathcal {G}\rightrightarrows X$ on a Poisson manifold ![]() $M$ with moment map
$M$ with moment map ![]() $\mu : M \longrightarrow X$ is Hamiltonian if its graph
$\mu : M \longrightarrow X$ is Hamiltonian if its graph
is coisotropic in ![]() $\mathcal {G} \times M \times M^{-}$. If the Poisson structure on
$\mathcal {G} \times M \times M^{-}$. If the Poisson structure on ![]() $M$ is induced by a symplectic form
$M$ is induced by a symplectic form ![]() $\omega$, we call
$\omega$, we call ![]() $((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$ a Hamiltonian system.
$((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$ a Hamiltonian system.
Remark 2.2 The moment map ![]() $\mu : M \longrightarrow X$ of a Hamiltonian system is automatically Poisson [Reference Mikami and WeinsteinMW88, Theorem 3.8]. Conversely, any Poisson map
$\mu : M \longrightarrow X$ of a Hamiltonian system is automatically Poisson [Reference Mikami and WeinsteinMW88, Theorem 3.8]. Conversely, any Poisson map ![]() $\mu : M \longrightarrow X$ from a symplectic manifold
$\mu : M \longrightarrow X$ from a symplectic manifold ![]() $M$ to a Poisson manifold
$M$ to a Poisson manifold ![]() $X$ uniquely determines an action of the symplectic local groupoid integrating
$X$ uniquely determines an action of the symplectic local groupoid integrating ![]() $X$ (see [Reference Costé, Dazord and WeinsteinCDW87, Chapitre III, Théorème 1.1]).
$X$ (see [Reference Costé, Dazord and WeinsteinCDW87, Chapitre III, Théorème 1.1]).
Remark 2.3 Each Lie group ![]() $G$ with Lie algebra
$G$ with Lie algebra ![]() $\mathfrak {g}$ has an associated symplectic groupoid
$\mathfrak {g}$ has an associated symplectic groupoid ![]() $T^{*}G\rightrightarrows \mathfrak {g}^{*}$. It has the property that Hamiltonian systems
$T^{*}G\rightrightarrows \mathfrak {g}^{*}$. It has the property that Hamiltonian systems ![]() $((M, \omega ), T^{*}G \rightrightarrows \mathfrak {g}^{*}, \mu )$ are equivalent to the more familiar Hamiltonian
$((M, \omega ), T^{*}G \rightrightarrows \mathfrak {g}^{*}, \mu )$ are equivalent to the more familiar Hamiltonian ![]() $G$-spaces. We refer the reader to § 4.1 for further details.
$G$-spaces. We refer the reader to § 4.1 for further details.
2.2 Pre-Poisson submanifolds and stabilizer subgroupoids
For a submanifold ![]() $S$ of a Poisson manifold
$S$ of a Poisson manifold ![]() $(X, \sigma )$, consider the subset of
$(X, \sigma )$, consider the subset of ![]() $T^{*}X$ given by
$T^{*}X$ given by
where ![]() $TS^{\circ }$ is the annihilator of
$TS^{\circ }$ is the annihilator of ![]() $TS$ in
$TS$ in ![]() $T^{*}X$. Our reduction procedure is based on the following class of submanifolds.
$T^{*}X$. Our reduction procedure is based on the following class of submanifolds.
Definition 2.4 (Cattaneo–Zambon [Reference Cattaneo and ZambonCZ07] and [Reference Cattaneo and ZambonCZ09, Definition 2.2])
A submanifold ![]() $S$ of a Poisson manifold
$S$ of a Poisson manifold ![]() $(X, \sigma )$ is called pre-Poisson if (2.3) has constant rank over
$(X, \sigma )$ is called pre-Poisson if (2.3) has constant rank over ![]() $S$.
$S$.
Remark 2.5 In [Reference Cattaneo and ZambonCZ07, Reference Cattaneo and ZambonCZ09], pre-Poisson submanifolds are defined by the condition that ![]() $\sigma (TS^{\circ }) + TS$ has constant rank. The two definitions are equivalent because
$\sigma (TS^{\circ }) + TS$ has constant rank. The two definitions are equivalent because ![]() $(\sigma (TS^{\circ }) + TS)^{\circ } = \sigma ^{-1}(TS) \cap TS^{\circ }$.
$(\sigma (TS^{\circ }) + TS)^{\circ } = \sigma ^{-1}(TS) \cap TS^{\circ }$.
Note that there is no constraint on the dimension of ![]() $S$. In fact, a generic submanifold is pre-Poisson in the following sense.
$S$. In fact, a generic submanifold is pre-Poisson in the following sense.
Proposition 2.6 For a generic point ![]() $x \in X$, a generic subspace
$x \in X$, a generic subspace ![]() $V \subseteq T_xX$, and an arbitrary submanifold
$V \subseteq T_xX$, and an arbitrary submanifold ![]() $S \subseteq X$ with
$S \subseteq X$ with ![]() $x \in S$ and
$x \in S$ and ![]() $T_xS = V$,
$T_xS = V$, ![]() $S$ is pre-Poisson in a neighborhood of
$S$ is pre-Poisson in a neighborhood of ![]() $x$.
$x$.
Proof. The term ‘generic’ used in this statement refers to an element of some fixed open dense set. The set of ![]() $x \in X$ such that
$x \in X$ such that ![]() $\sigma$ has constant rank in a neighborhood of
$\sigma$ has constant rank in a neighborhood of ![]() $x$ is open and dense, so this reduces to the case of a Poisson vector space
$x$ is open and dense, so this reduces to the case of a Poisson vector space ![]() $(W, \sigma )$. The proposition then follows from the fact that the set of
$(W, \sigma )$. The proposition then follows from the fact that the set of ![]() $k$-dimensional subspaces
$k$-dimensional subspaces ![]() $V \subseteq W$ such that
$V \subseteq W$ such that ![]() $V + \sigma (V^{\circ })$ has maximal dimension is open and dense in the Grassmannian of
$V + \sigma (V^{\circ })$ has maximal dimension is open and dense in the Grassmannian of ![]() $k$-planes in
$k$-planes in ![]() $W$.
$W$.
We have the following important result on pre-Poisson submanifolds.
Theorem 2.7 (Cattaneo–Zambon [Reference Cattaneo and ZambonCZ09, Proposition 3.6 and Proposition 7.2])
Let ![]() $\mathcal {G} \rightrightarrows X$ be a symplectic groupoid and
$\mathcal {G} \rightrightarrows X$ be a symplectic groupoid and ![]() $S \subseteq X$ a pre-Poisson submanifold.
$S \subseteq X$ a pre-Poisson submanifold.
(i) The subset
 $L_S$ of
$L_S$ of  $T^{*}X$ given by (2.3) is a Lie subalgebroid of
$T^{*}X$ given by (2.3) is a Lie subalgebroid of  $\operatorname {Lie}(\mathcal {G}) = T^{*}X$.
$\operatorname {Lie}(\mathcal {G}) = T^{*}X$.(ii) The ssc Lie groupoid
 $\mathcal {G}_S \rightrightarrows S$ with Lie algebroid
$\mathcal {G}_S \rightrightarrows S$ with Lie algebroid  $L_S$ is isotropic in
$L_S$ is isotropic in  $\mathcal {G}$.
$\mathcal {G}$.
Part (ii) requires further explanation. First, recall that a Lie subalgebroid of an integrable Lie algebroid is integrable [Reference Moerdijk and MrčunMM02, Proposition 3.4]. It follows from part (i) that ![]() $L_S$ integrates to an ssc Lie groupoid
$L_S$ integrates to an ssc Lie groupoid ![]() $\mathcal {G}_S \rightrightarrows S$ together with an immersion
$\mathcal {G}_S \rightrightarrows S$ together with an immersion ![]() $\mathcal {G}_S \longrightarrow \mathcal {G}$ (see [Reference Moerdijk and MrčunMM02, Proposition 3.5]). The condition that
$\mathcal {G}_S \longrightarrow \mathcal {G}$ (see [Reference Moerdijk and MrčunMM02, Proposition 3.5]). The condition that ![]() $\mathcal {G}_S$ is isotropic in
$\mathcal {G}_S$ is isotropic in ![]() $\mathcal {G}$ then means that the pullback of the symplectic form on
$\mathcal {G}$ then means that the pullback of the symplectic form on ![]() $\mathcal {G}$ to
$\mathcal {G}$ to ![]() $\mathcal {G}_S$ vanishes.
$\mathcal {G}_S$ vanishes.
In this paper, we follow the convention that a Lie subgroupoid of a Lie groupoid ![]() $\mathcal {G}$ is a Lie groupoid
$\mathcal {G}$ is a Lie groupoid ![]() $\mathcal {H}$ together with a possibly non-injective immersion
$\mathcal {H}$ together with a possibly non-injective immersion ![]() $\mathcal {H} \longrightarrow \mathcal {G}$ that is also a Lie groupoid homomorphism. The groupoid
$\mathcal {H} \longrightarrow \mathcal {G}$ that is also a Lie groupoid homomorphism. The groupoid ![]() $\mathcal {G}_S \rightrightarrows S$ in Theorem 2.7 is therefore an isotropic Lie subgroupoid of
$\mathcal {G}_S \rightrightarrows S$ in Theorem 2.7 is therefore an isotropic Lie subgroupoid of ![]() $\mathcal {G} \rightrightarrows S$. These considerations motivate the following definition.
$\mathcal {G} \rightrightarrows S$. These considerations motivate the following definition.
Definition 2.8 Let ![]() $\mathcal {G} \rightrightarrows X$ be a symplectic groupoid and
$\mathcal {G} \rightrightarrows X$ be a symplectic groupoid and ![]() $S \subseteq X$ a pre-Poisson submanifold. The Lie algebroid
$S \subseteq X$ a pre-Poisson submanifold. The Lie algebroid ![]() $L_S$ defined in (2.3) is called the stabilizer subalgebroid of
$L_S$ defined in (2.3) is called the stabilizer subalgebroid of ![]() $S$. A stabilizer subgroupoid of
$S$. A stabilizer subgroupoid of ![]() $S$ in
$S$ in ![]() $\mathcal {G}$ is any (possibly non-source-connected) isotropic Lie subgroupoid
$\mathcal {G}$ is any (possibly non-source-connected) isotropic Lie subgroupoid ![]() $\mathcal {H} \rightrightarrows S$ of
$\mathcal {H} \rightrightarrows S$ of ![]() $\mathcal {G} \rightrightarrows X$ with Lie algebroid
$\mathcal {G} \rightrightarrows X$ with Lie algebroid ![]() $L_S$. The unique ssc stabilizer subgroupoid of
$L_S$. The unique ssc stabilizer subgroupoid of ![]() $S$ in
$S$ in ![]() $\mathcal {G}$ is denoted
$\mathcal {G}$ is denoted ![]() $\mathcal {G}_S \rightrightarrows S$.
$\mathcal {G}_S \rightrightarrows S$.
Remark 2.9 (i) This terminology is justified by the fact that stabilizer subgroupoids generalize stabilizer subgroups in Marsden–Weinstein–Meyer reduction, which we explain in § 4.2.
(ii) By [Reference Cattaneo and ZambonCZ09, Proposition 7.2], any source-connected Lie subgroupoid ![]() $\mathcal {H} \rightrightarrows S$ of
$\mathcal {H} \rightrightarrows S$ of ![]() $\mathcal {G} \rightrightarrows X$ with Lie algebroid
$\mathcal {G} \rightrightarrows X$ with Lie algebroid ![]() $L_S$ is isotropic, and hence a stabilizer subgroupoid. More generally, if
$L_S$ is isotropic, and hence a stabilizer subgroupoid. More generally, if ![]() $\mathcal {H}$ is source-connected over an open dense subset of
$\mathcal {H}$ is source-connected over an open dense subset of ![]() $S$, then it is isotropic.
$S$, then it is isotropic.
(iii) On the other hand, a non-source-connected Lie subgroupoid ![]() $\mathcal {H} \rightrightarrows S$ with Lie algebroid
$\mathcal {H} \rightrightarrows S$ with Lie algebroid ![]() $L_S$ might not be isotropic. For example,Footnote 3 let
$L_S$ might not be isotropic. For example,Footnote 3 let ![]() $X$ be a smooth manifold with the zero Poisson structure
$X$ be a smooth manifold with the zero Poisson structure ![]() $\sigma = 0$. Then
$\sigma = 0$. Then ![]() $\mathcal {G} = T^{*}X$ with its canonical symplectic form is a symplectic groupoid integrating
$\mathcal {G} = T^{*}X$ with its canonical symplectic form is a symplectic groupoid integrating ![]() $X$ (see [Reference Costé, Dazord and WeinsteinCDW87, Ch. II, Example 3.3]). Consider
$X$ (see [Reference Costé, Dazord and WeinsteinCDW87, Ch. II, Example 3.3]). Consider ![]() $S = X$, so that
$S = X$, so that ![]() $L_S$ is trivial. For any non-vanishing
$L_S$ is trivial. For any non-vanishing ![]() $1$-form
$1$-form ![]() $\alpha$ on
$\alpha$ on ![]() $X$,
$X$,
is a Lie subgroupoid of ![]() $\mathcal {G} = T^{*}X$ with Lie algebroid
$\mathcal {G} = T^{*}X$ with Lie algebroid ![]() $L_S = 0$. However, the pullback of the canonical symplectic form on
$L_S = 0$. However, the pullback of the canonical symplectic form on ![]() $T^{*}X$ by
$T^{*}X$ by ![]() $\alpha : X \longrightarrow T^{*}X$ is
$\alpha : X \longrightarrow T^{*}X$ is ![]() $d\alpha$. It follows that
$d\alpha$. It follows that ![]() $\mathcal {H}$ is isotropic if and only if
$\mathcal {H}$ is isotropic if and only if ![]() $\alpha$ is closed.
$\alpha$ is closed.
(iv) One explanation for the isotropy condition is that stabilizer subgroupoids are precisely the Lie subgroupoids of ![]() $\mathcal {G}$ for which the map of quotient stacks
$\mathcal {G}$ for which the map of quotient stacks ![]() $[S/\mathcal {H}] \longrightarrow [X/\mathcal {G}]$ has a canonical Lagrangian structure. This is explained in § 6.
$[S/\mathcal {H}] \longrightarrow [X/\mathcal {G}]$ has a canonical Lagrangian structure. This is explained in § 6.
Another important result of [Reference Cattaneo and ZambonCZ09] is that pre-Poisson submanifolds can be embedded coisotropically in Poisson transversals, as we now recall.
We begin by recalling that a submanifold ![]() $Y$ of a Poisson manifold
$Y$ of a Poisson manifold ![]() $(X, \sigma )$ is called a Poisson transversal (or sometimes a cosymplectic submanifold) if
$(X, \sigma )$ is called a Poisson transversal (or sometimes a cosymplectic submanifold) if ![]() $Y$ intersects every symplectic leaf transversally and in a symplectic submanifold of the leaf [Reference Frejlich and MarcutFM17]. Equivalently,
$Y$ intersects every symplectic leaf transversally and in a symplectic submanifold of the leaf [Reference Frejlich and MarcutFM17]. Equivalently, ![]() $Y$ is Poisson transversal if
$Y$ is Poisson transversal if
In this case, ![]() $Y$ inherits a canonical Poisson structure from
$Y$ inherits a canonical Poisson structure from ![]() $X$ (see [Reference Frejlich and MarcutFM17, Lemma 3]). To describe this Poisson structure as a bivector field
$X$ (see [Reference Frejlich and MarcutFM17, Lemma 3]). To describe this Poisson structure as a bivector field ![]() $\sigma _Y:T^{*}Y \longrightarrow TY$, note that the restriction of linear functionals defines an isomorphism
$\sigma _Y:T^{*}Y \longrightarrow TY$, note that the restriction of linear functionals defines an isomorphism ![]() $\sigma ^{-1}(TY) \longrightarrow T^{*}Y$. One then defines
$\sigma ^{-1}(TY) \longrightarrow T^{*}Y$. One then defines ![]() $\sigma _Y$ by
$\sigma _Y$ by ![]() $\sigma _Y(\xi ) = \sigma (\hat {\xi })$, where
$\sigma _Y(\xi ) = \sigma (\hat {\xi })$, where ![]() $\hat {\xi }$ is the unique element of
$\hat {\xi }$ is the unique element of ![]() $\sigma ^{-1}(TY)$ mapping to
$\sigma ^{-1}(TY)$ mapping to ![]() $\xi \in T^{*}Y$.
$\xi \in T^{*}Y$.
Cattaneo and Zambon [Reference Cattaneo and ZambonCZ09] prove that every pre-Poisson submanifold ![]() $S$ of a Poisson submanifold
$S$ of a Poisson submanifold ![]() $(X, \sigma )$ can be embedded in a Poisson transversal
$(X, \sigma )$ can be embedded in a Poisson transversal ![]() $Y \subseteq X$ such that
$Y \subseteq X$ such that ![]() $S$ is coisotropic in
$S$ is coisotropic in ![]() $Y$ (see [Reference Cattaneo and ZambonCZ09, Theorem 3.3]).
$Y$ (see [Reference Cattaneo and ZambonCZ09, Theorem 3.3]).
2.3 Symplectic reduction along a submanifold
Let ![]() $\mu : M \longrightarrow X$ be a smooth map between smooth manifolds. We say that a submanifold
$\mu : M \longrightarrow X$ be a smooth map between smooth manifolds. We say that a submanifold ![]() $S \subseteq X$ intersects
$S \subseteq X$ intersects ![]() $\mu$ cleanly if
$\mu$ cleanly if ![]() $\mu ^{-1}(S)$ is a submanifold of
$\mu ^{-1}(S)$ is a submanifold of ![]() $M$ satisfying
$M$ satisfying
for all ![]() $p \in \mu ^{-1}(S)$. Recall that this condition is satisfied if
$p \in \mu ^{-1}(S)$. Recall that this condition is satisfied if ![]() $S$ is transverse to
$S$ is transverse to ![]() $\mu$, i.e. if
$\mu$, i.e. if
for all ![]() $p \in \mu ^{-1}(S)$.
$p \in \mu ^{-1}(S)$.
We are now equipped to begin proving Theorem A from the introduction. The main idea is that for a Hamiltonian system ![]() $((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$, pre-Poisson submanifold
$((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$, pre-Poisson submanifold ![]() $S \subseteq X$, and stabilizer subgroupoid
$S \subseteq X$, and stabilizer subgroupoid ![]() $\mathcal {H} \rightrightarrows S$, the distribution defined by the kernel of the restriction of
$\mathcal {H} \rightrightarrows S$, the distribution defined by the kernel of the restriction of ![]() $\omega$ to
$\omega$ to ![]() $\mu ^{-1}(S)$ coincides with the orbits of the
$\mu ^{-1}(S)$ coincides with the orbits of the ![]() $\mathcal {H}$-action. This result can be stated more generally for Poisson manifolds.
$\mathcal {H}$-action. This result can be stated more generally for Poisson manifolds.
Theorem 2.10 Let ![]() $\mathcal {G} \rightrightarrows X$ be a symplectic groupoid acting on a Poisson manifold
$\mathcal {G} \rightrightarrows X$ be a symplectic groupoid acting on a Poisson manifold ![]() $(M, \tau )$ in a Hamiltonian way with moment map
$(M, \tau )$ in a Hamiltonian way with moment map ![]() $\mu : M \longrightarrow X$. Let
$\mu : M \longrightarrow X$. Let ![]() $S \subseteq X$ be a pre-Poisson submanifold intersecting
$S \subseteq X$ be a pre-Poisson submanifold intersecting ![]() $\mu$ cleanly, let
$\mu$ cleanly, let ![]() $\mathcal {H} \rightrightarrows S$ be a stabilizer subgroupoid of
$\mathcal {H} \rightrightarrows S$ be a stabilizer subgroupoid of ![]() $S$ in
$S$ in ![]() $\mathcal {G}$, and let
$\mathcal {G}$, and let ![]() $N := \mu ^{-1}(S)$. We then have
$N := \mu ^{-1}(S)$. We then have
for all ![]() $p \in N$.
$p \in N$.
To prove this theorem, we begin with a few lemmas. Let ![]() $((M, \tau ), \mathcal {G} \rightrightarrows X, \mu )$,
$((M, \tau ), \mathcal {G} \rightrightarrows X, \mu )$, ![]() $\mathcal {H} \rightrightarrows S$, and
$\mathcal {H} \rightrightarrows S$, and ![]() $N$ be as in Theorem 2.10.
$N$ be as in Theorem 2.10.
Lemma 2.11 We have
for all ![]() $x \in S$, where
$x \in S$, where ![]() $\Omega$ is the symplectic form on
$\Omega$ is the symplectic form on ![]() $\mathcal {G}$.
$\mathcal {G}$.
Proof. Let ![]() $\varphi : (\ker d\mathsf {t})\vert _X \longrightarrow T^{*}X$ be the isomorphism given by (2.2), so that
$\varphi : (\ker d\mathsf {t})\vert _X \longrightarrow T^{*}X$ be the isomorphism given by (2.2), so that
Let ![]() $x \in S$. The definition of
$x \in S$. The definition of ![]() $\mathcal {H}$ then implies that
$\mathcal {H}$ then implies that
It follows that
However, ![]() $T_xS \subseteq T_xS^{\Omega }$ because
$T_xS \subseteq T_xS^{\Omega }$ because ![]() $X$ is Lagrangian in
$X$ is Lagrangian in ![]() $\mathcal {G}$, so
$\mathcal {G}$, so
Denote the action map by ![]() $\psi : \mathcal {G}_{\mathsf {t}}{\times }_\mu M \longrightarrow M$ and the orbit map at a point
$\psi : \mathcal {G}_{\mathsf {t}}{\times }_\mu M \longrightarrow M$ and the orbit map at a point ![]() $p \in M$ over
$p \in M$ over ![]() $x := \mu (p) \in X$ by
$x := \mu (p) \in X$ by
where ![]() $\mathcal {G}_x := \mathsf {t}^{-1}(x)$. If
$\mathcal {G}_x := \mathsf {t}^{-1}(x)$. If ![]() $p \in N$, then
$p \in N$, then ![]() $T_p(\mathcal {H} \cdot p)$ is the image of
$T_p(\mathcal {H} \cdot p)$ is the image of ![]() $T_x\mathcal {H}_x$ under
$T_x\mathcal {H}_x$ under ![]() $d\psi _p$.
$d\psi _p$.
Lemma 2.12 For all ![]() $f \in C^{\infty }(X)$ and
$f \in C^{\infty }(X)$ and ![]() $(g, p) \in \mathcal {G} \times _X M$, we have
$(g, p) \in \mathcal {G} \times _X M$, we have
Proof. Consider the map
The graph ![]() $\Gamma$ of the action is coisotropic and
$\Gamma$ of the action is coisotropic and ![]() $F\vert _\Gamma = 0$, so
$F\vert _\Gamma = 0$, so ![]() $X_F$ is tangent to
$X_F$ is tangent to ![]() $\Gamma$. However,
$\Gamma$. However,
so ![]() $X_F = (X_{\mathsf {s}^{*}f}, 0, X_{\mu ^{*}f})$. Hence,
$X_F = (X_{\mathsf {s}^{*}f}, 0, X_{\mu ^{*}f})$. Hence,
for some ![]() $(u, v) \in T_{(g, p)}(\mathcal {G} \times _X M)$, which implies that
$(u, v) \in T_{(g, p)}(\mathcal {G} \times _X M)$, which implies that ![]() $v = 0$ and
$v = 0$ and ![]() $u = X_{\mathsf {s}^{*}f}(g)$. We conclude that
$u = X_{\mathsf {s}^{*}f}(g)$. We conclude that
Lemma 2.13 Let ![]() $x \in S$ and
$x \in S$ and ![]() $v \in T_x\mathcal {G}$. Then
$v \in T_x\mathcal {G}$. Then ![]() $v \in T_x\mathcal {H}_x$ if and only if
$v \in T_x\mathcal {H}_x$ if and only if ![]() $v = X_{\mathsf {s}^{*}f}(x)$ for some
$v = X_{\mathsf {s}^{*}f}(x)$ for some ![]() $f \in C^{\infty }(X)$ such that
$f \in C^{\infty }(X)$ such that ![]() $f\vert _S = 0$ and
$f\vert _S = 0$ and ![]() $X_f(x) \in T_xS$.
$X_f(x) \in T_xS$.
Proof. By Lemma 2.11, we have
Let ![]() $v = X_{\mathsf {s}^{*}f}(x)$ be as stated. Then
$v = X_{\mathsf {s}^{*}f}(x)$ be as stated. Then ![]() $d\mathsf {t}(v) = 0$ (see [Reference Mikami and WeinsteinMW88, Theorem 1.6(i)]),
$d\mathsf {t}(v) = 0$ (see [Reference Mikami and WeinsteinMW88, Theorem 1.6(i)]), ![]() $d\mathsf {s}(v) = X_f(x) \in T_xS$ because
$d\mathsf {s}(v) = X_f(x) \in T_xS$ because ![]() $\mathsf {s}$ is a Poisson map, and
$\mathsf {s}$ is a Poisson map, and
Hence, ![]() $v \in T_x\mathcal {H}_x$ by (2.4).
$v \in T_x\mathcal {H}_x$ by (2.4).
Conversely, let ![]() $v \in T_x\mathcal {H}_x$. By (2.4), we have
$v \in T_x\mathcal {H}_x$. By (2.4), we have ![]() $d\mathsf {t}(v) = 0$,
$d\mathsf {t}(v) = 0$, ![]() $d\mathsf {s}(v) \in T_xS$ and
$d\mathsf {s}(v) \in T_xS$ and ![]() $\Omega (v)\vert _{T_xX} \in T_xS^{\circ }$. The latter implies that
$\Omega (v)\vert _{T_xX} \in T_xS^{\circ }$. The latter implies that ![]() $\Omega (v)\vert _{T_xX} = df_x$ for some
$\Omega (v)\vert _{T_xX} = df_x$ for some ![]() $f \in C^{\infty }(X)$ such that
$f \in C^{\infty }(X)$ such that ![]() $f\vert _S = 0$. Then
$f\vert _S = 0$. Then ![]() $\Omega (v) = df \circ d\mathsf {s}_x$ because
$\Omega (v) = df \circ d\mathsf {s}_x$ because ![]() $T_x\mathcal {G} = T_xX \oplus \ker d\mathsf {s}_x$ and
$T_x\mathcal {G} = T_xX \oplus \ker d\mathsf {s}_x$ and ![]() $(\ker d\mathsf {s}_x)^{\Omega } = \ker d\mathsf {t}$. It follows that
$(\ker d\mathsf {s}_x)^{\Omega } = \ker d\mathsf {t}$. It follows that ![]() $v = X_{\mathsf {s}^{*}f}(x)$ and
$v = X_{\mathsf {s}^{*}f}(x)$ and ![]() $X_f(x) = d\mathsf {s}(v) \in T_xS$.
$X_f(x) = d\mathsf {s}(v) \in T_xS$.
We now prove Theorem 2.10.
Proof of Theorem 2.10 To show that
let ![]() $x := \mu (p)$ and
$x := \mu (p)$ and ![]() $v \in T_x\mathcal {H}_x$. Note that
$v \in T_x\mathcal {H}_x$. Note that
Then ![]() $u \in T_pN$ because
$u \in T_pN$ because ![]() $\mathcal {H}$ acts on
$\mathcal {H}$ acts on ![]() $N$. By Lemma 2.13, we have
$N$. By Lemma 2.13, we have ![]() $v = X_{\mathsf {s}^{*}f}(x)$ for some
$v = X_{\mathsf {s}^{*}f}(x)$ for some ![]() $f \in C^{\infty }(X)$ with
$f \in C^{\infty }(X)$ with ![]() $f\vert _S = 0$ and
$f\vert _S = 0$ and ![]() $X_f(x) \in T_xS$, and by Lemma 2.12,
$X_f(x) \in T_xS$, and by Lemma 2.12,
However, ![]() $d\mu (X_{\mu ^{*}f}(p)) = X_f(x) \in T_xS$ since
$d\mu (X_{\mu ^{*}f}(p)) = X_f(x) \in T_xS$ since ![]() $\mu$ is a Poisson map; this follows from [Reference Mikami and WeinsteinMW88, Theorem 3.8], as explained in [Reference Bursztyn and CrainicBC05, § 4.2]. Hence,
$\mu$ is a Poisson map; this follows from [Reference Mikami and WeinsteinMW88, Theorem 3.8], as explained in [Reference Bursztyn and CrainicBC05, § 4.2]. Hence, ![]() $u \in T_pN$. We also have
$u \in T_pN$. We also have
so ![]() $u = X_{\mu ^{*}f}(p) \in \tau (T_pN^{\circ })$.
$u = X_{\mu ^{*}f}(p) \in \tau (T_pN^{\circ })$.
Conversely, let ![]() $v \in T_pN \cap \tau (T_pN^{\circ })$. As
$v \in T_pN \cap \tau (T_pN^{\circ })$. As
we have ![]() $v = X_{\mu ^{*}f}(p)$ for some
$v = X_{\mu ^{*}f}(p)$ for some ![]() $f \in C^{\infty }(X)$ with
$f \in C^{\infty }(X)$ with ![]() $f\vert _S = 0$. We also have
$f\vert _S = 0$. We also have
We thus have ![]() $X_{\mathsf {s}^{*}f}(x) \in T_x\mathcal {H}_x$ by Lemma 2.13 and
$X_{\mathsf {s}^{*}f}(x) \in T_x\mathcal {H}_x$ by Lemma 2.13 and ![]() $v = d\psi _p(X_{\mathsf {s}^{*}f}(x))$ by Lemma 2.12, so
$v = d\psi _p(X_{\mathsf {s}^{*}f}(x))$ by Lemma 2.12, so ![]() $v \in T_p(\mathcal {H} \cdot p)$.
$v \in T_p(\mathcal {H} \cdot p)$.
The main theorem of this section is the following generalization of Mikami–Weinstein reduction.
Theorem 2.14 (Theorem A(i))
Let ![]() $((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$ be a Hamiltonian system,
$((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$ be a Hamiltonian system, ![]() $S \subseteq X$ a pre-Poisson submanifold,
$S \subseteq X$ a pre-Poisson submanifold, ![]() $\mathcal {H} \rightrightarrows S$ a stabilizer subgroupoid of
$\mathcal {H} \rightrightarrows S$ a stabilizer subgroupoid of ![]() $S$ in
$S$ in ![]() $\mathcal {G}$, and
$\mathcal {G}$, and ![]() $N := \mu ^{-1}(S)$. Suppose that
$N := \mu ^{-1}(S)$. Suppose that ![]() $S$ intersects
$S$ intersects ![]() $\mu$ cleanly and that
$\mu$ cleanly and that ![]() $N / \mathcal {H}$ has the structure of a smooth manifold for which the quotient map
$N / \mathcal {H}$ has the structure of a smooth manifold for which the quotient map ![]() $\pi : N \longrightarrow N / \mathcal {H}$ is a smooth submersion. Then there is a unique symplectic form
$\pi : N \longrightarrow N / \mathcal {H}$ is a smooth submersion. Then there is a unique symplectic form ![]() $\bar {\omega }$ on
$\bar {\omega }$ on ![]() $N / \mathcal {H}$ satisfying
$N / \mathcal {H}$ satisfying ![]() $\pi ^{*}\bar {\omega } = i^{*}\omega$, where
$\pi ^{*}\bar {\omega } = i^{*}\omega$, where ![]() $i : N \longrightarrow M$ is the inclusion map.
$i : N \longrightarrow M$ is the inclusion map.
Proof. We have ![]() $\ker d\pi _p = T_p(\mathcal {H} \cdot p)$ for all
$\ker d\pi _p = T_p(\mathcal {H} \cdot p)$ for all ![]() $p \in N$ by assumption. Hence, as in standard symplectic reduction [Reference Marsden and WeinsteinMW74, Reference Mikami and WeinsteinMW88], it suffices to show that the distribution
$p \in N$ by assumption. Hence, as in standard symplectic reduction [Reference Marsden and WeinsteinMW74, Reference Mikami and WeinsteinMW88], it suffices to show that the distribution ![]() $\ker (i^{*}\omega ) = TN \cap TN^{\omega }$ on
$\ker (i^{*}\omega ) = TN \cap TN^{\omega }$ on ![]() $N$ coincides with that induced by the
$N$ coincides with that induced by the ![]() $\mathcal {H}$-orbits. This is precisely the content of Theorem 2.10.
$\mathcal {H}$-orbits. This is precisely the content of Theorem 2.10.
Definition 2.15 Let ![]() $((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$ be a Hamiltonian system. A reduction datum is a pair
$((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$ be a Hamiltonian system. A reduction datum is a pair ![]() $(S, \mathcal {H})$, where
$(S, \mathcal {H})$, where ![]() $S$ is a pre-Poisson submanifold of
$S$ is a pre-Poisson submanifold of ![]() $X$ and
$X$ and ![]() $\mathcal {H}\rightrightarrows S$ is a stabilizer subgroupoid of
$\mathcal {H}\rightrightarrows S$ is a stabilizer subgroupoid of ![]() $S$ in
$S$ in ![]() $\mathcal {G}$. The quotient topological space
$\mathcal {G}$. The quotient topological space ![]() $\mu ^{-1}(S) / \mathcal {H}$ is called the symplectic reduction of
$\mu ^{-1}(S) / \mathcal {H}$ is called the symplectic reduction of ![]() $M$ by
$M$ by ![]() $\mathcal {G}$ along
$\mathcal {G}$ along ![]() $S$ with respect to
$S$ with respect to ![]() $\mathcal {H}$ and denoted
$\mathcal {H}$ and denoted
We say that the reduction datum ![]() $(S, \mathcal {H})$ is clean if the assumptions of Theorem 2.14 are satisfied, in which case
$(S, \mathcal {H})$ is clean if the assumptions of Theorem 2.14 are satisfied, in which case ![]() $M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S, \mathcal {H}}} \mathcal {G}$ is a symplectic manifold. If
$M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S, \mathcal {H}}} \mathcal {G}$ is a symplectic manifold. If ![]() $\mathcal {H}$ is source-connected, we use the simplified notation
$\mathcal {H}$ is source-connected, we use the simplified notation
and terminology symplectic reduction of ![]() $M$ by
$M$ by ![]() $\mathcal {G}$ along
$\mathcal {G}$ along ![]() $S$.
$S$.
Remark 2.16 The quotient ![]() $M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S, \mathcal {H}}} \mathcal {G}$ depends on
$M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S, \mathcal {H}}} \mathcal {G}$ depends on ![]() $\mathcal {H}$ only up to its image in
$\mathcal {H}$ only up to its image in ![]() $\mathcal {G}$. In particular,
$\mathcal {G}$. In particular, ![]() $M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S, \mathcal {H}}} \mathcal {G} = M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S, \mathcal {G}_S}} \mathcal {G}$ for any source-connected stabilizer subgroupoid
$M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S, \mathcal {H}}} \mathcal {G} = M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S, \mathcal {G}_S}} \mathcal {G}$ for any source-connected stabilizer subgroupoid ![]() $\mathcal {H}$ of
$\mathcal {H}$ of ![]() $S$ in
$S$ in ![]() $\mathcal {G}$. This explains and justifies the simplified notation
$\mathcal {G}$. This explains and justifies the simplified notation ![]() $M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S}} \mathcal {G}$.
$M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S}} \mathcal {G}$.
Remark 2.17 More generally, let ![]() $S \subseteq X$ be a stratified space whose strata are pre-Poisson submanifolds
$S \subseteq X$ be a stratified space whose strata are pre-Poisson submanifolds ![]() $S_i$ of
$S_i$ of ![]() $X$. For a collection of stabilizer subgroupoids
$X$. For a collection of stabilizer subgroupoids ![]() $\mathcal {H} = (\mathcal {H}_i \rightrightarrows S_i)_i$, we may define
$\mathcal {H} = (\mathcal {H}_i \rightrightarrows S_i)_i$, we may define
and regard it as a topological quotient of ![]() $\mu ^{-1}(S)$. This notion will be useful when discussing symplectic implosion (§ 4.7) and symplectic cutting (§ 4.8).
$\mu ^{-1}(S)$. This notion will be useful when discussing symplectic implosion (§ 4.7) and symplectic cutting (§ 4.8).
Remark 2.18 Suppose that we had assumed ![]() $\mathcal {H}$ to be source-connected in Theorem 2.14. The theorem could then be viewed as a special case reduction along a pre-symplectic submanifold, i.e. a submanifold
$\mathcal {H}$ to be source-connected in Theorem 2.14. The theorem could then be viewed as a special case reduction along a pre-symplectic submanifold, i.e. a submanifold ![]() $i: N \hookrightarrow M$ such that
$i: N \hookrightarrow M$ such that ![]() $i^{*}\omega$ has constant rank. The distribution
$i^{*}\omega$ has constant rank. The distribution ![]() $\ker (i^{*}\omega ) \subseteq TN$ would then necessarily be integrable, so that the leaf space would symplectic when smooth [Reference Guillemin and SternbergGS84, Theorem 25.2]. The essence of Theorem 2.14 is as follows: if
$\ker (i^{*}\omega ) \subseteq TN$ would then necessarily be integrable, so that the leaf space would symplectic when smooth [Reference Guillemin and SternbergGS84, Theorem 25.2]. The essence of Theorem 2.14 is as follows: if ![]() $\mu : M \longrightarrow X$ is a Poisson map, then for any pre-Poisson submanifold
$\mu : M \longrightarrow X$ is a Poisson map, then for any pre-Poisson submanifold ![]() $S \subseteq X$, the leaves in
$S \subseteq X$, the leaves in ![]() $N := \mu ^{-1}(S)$ are explicitly realized as the orbits of a groupoid action.
$N := \mu ^{-1}(S)$ are explicitly realized as the orbits of a groupoid action.
2.4 A sufficient condition for smoothness
In the context of Marsden–Weinstein–Meyer reduction, one knows that zero is a regular value of the moment map if the Hamiltonian action in question is free. The goal of this section is to generalize this classical fact to our setting.
Let ![]() $((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$ be a Hamiltonian system, let
$((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$ be a Hamiltonian system, let ![]() $(S, \mathcal {H})$ be a reduction datum, and let
$(S, \mathcal {H})$ be a reduction datum, and let ![]() $N := \mu ^{-1}(S)$.
$N := \mu ^{-1}(S)$.
Proposition 2.19 Let ![]() $p \in N$, let
$p \in N$, let ![]() $x := \mu (p)$, and let
$x := \mu (p)$, and let ![]() $\varphi _p : \mathcal {H}_x \longrightarrow N$ be the orbit map
$\varphi _p : \mathcal {H}_x \longrightarrow N$ be the orbit map ![]() $\varphi _p(h) = h \cdot x$. We have
$\varphi _p(h) = h \cdot x$. We have
where ![]() $\ker (d\varphi _p)_x$ is viewed as a subspace of
$\ker (d\varphi _p)_x$ is viewed as a subspace of ![]() $T_x^{*}X$ via the isomorphism (2.2).
$T_x^{*}X$ via the isomorphism (2.2).
Proof. Regarding ![]() $\ker (d\varphi _p)_x$ as a subspace of
$\ker (d\varphi _p)_x$ as a subspace of ![]() $T_x\mathcal {H}_x \subseteq T_x\mathcal {G}$, the statement can be reformulated as
$T_x\mathcal {H}_x \subseteq T_x\mathcal {G}$, the statement can be reformulated as
We prove this reformulated version in the following.
Lemma 2.11 tells us that
so
To show that ![]() $\operatorname {im} d\mu _p \subseteq (\ker (d\varphi _p)_x)^{\Omega }$, let
$\operatorname {im} d\mu _p \subseteq (\ker (d\varphi _p)_x)^{\Omega }$, let ![]() $v \in T_pM$ and
$v \in T_pM$ and ![]() $w \in \ker (d\varphi _p)_x$. By Lemma 2.13,
$w \in \ker (d\varphi _p)_x$. By Lemma 2.13, ![]() $w = X_{\mathsf {s}^{*}f}(x)$ for some
$w = X_{\mathsf {s}^{*}f}(x)$ for some ![]() $f \in C^{\infty }(X)$ such that
$f \in C^{\infty }(X)$ such that ![]() $f\vert _S = 0$ and
$f\vert _S = 0$ and ![]() $X_f(x) \in T_xS$. Lemma 2.12 then shows that
$X_f(x) \in T_xS$. Lemma 2.12 then shows that ![]() $X_{\mu ^{*}f}(p) = d\varphi _p(w) = 0$, so
$X_{\mu ^{*}f}(p) = d\varphi _p(w) = 0$, so ![]() $d(\mu ^{*}f)_p = 0$. It follows that
$d(\mu ^{*}f)_p = 0$. It follows that
It remains only to show that
where all annihilators are taken in ![]() $T^{*}_x\mathcal {G}$. To this end, let
$T^{*}_x\mathcal {G}$. To this end, let ![]() $\xi \in T_xS^{\circ } \cap (\operatorname {im} d\mu _p)^{\circ }$ and write
$\xi \in T_xS^{\circ } \cap (\operatorname {im} d\mu _p)^{\circ }$ and write ![]() $\xi \vert _{T_xX} = \Omega (v)\vert _{T_xX}$ with
$\xi \vert _{T_xX} = \Omega (v)\vert _{T_xX}$ with ![]() $v \in \ker d\mathsf {t}_x$. It then suffices to prove that
$v \in \ker d\mathsf {t}_x$. It then suffices to prove that ![]() $v \in T_x\mathcal {H}_x$ and
$v \in T_x\mathcal {H}_x$ and ![]() $d\varphi _p(v) = 0$. We begin by verifying that
$d\varphi _p(v) = 0$. We begin by verifying that ![]() $v \in T_x\mathcal {H}_x$. First note that
$v \in T_x\mathcal {H}_x$. First note that ![]() $v \in \ker d\mathsf {t}_x \cap (T_xS)^{\Omega }$. By Lemma 2.11, showing that
$v \in \ker d\mathsf {t}_x \cap (T_xS)^{\Omega }$. By Lemma 2.11, showing that ![]() $d\mathsf {s}(v) \in T_xS$ would suffice to prove that
$d\mathsf {s}(v) \in T_xS$ would suffice to prove that ![]() $v \in T_x\mathcal {H}_x$. As
$v \in T_x\mathcal {H}_x$. As ![]() $\mu$ is Poisson, we have
$\mu$ is Poisson, we have
and the latter is ![]() $0$ because
$0$ because ![]() $\xi \in (\operatorname {im} d\mu _p)^{\circ }$. It follows that
$\xi \in (\operatorname {im} d\mu _p)^{\circ }$. It follows that ![]() $v \in T_x\mathcal {H}_x$. To show that
$v \in T_x\mathcal {H}_x$. To show that ![]() $d\varphi _p(v) = 0$, first note that Lemma 2.13 implies that
$d\varphi _p(v) = 0$, first note that Lemma 2.13 implies that ![]() $v = X_{\mathsf {s}^{*}f}(x)$ for some
$v = X_{\mathsf {s}^{*}f}(x)$ for some ![]() $f \in C^{\infty }(X)$ such that
$f \in C^{\infty }(X)$ such that ![]() $f\vert _S = 0$ and
$f\vert _S = 0$ and ![]() $X_f(x) \in T_xX$. However,
$X_f(x) \in T_xX$. However,
so ![]() $d(\mu ^{*}f)_p = 0$ and hence
$d(\mu ^{*}f)_p = 0$ and hence ![]() $d\varphi _p(v) = X_{\mu ^{*}f}(p) = 0$ by Lemma 2.12.
$d\varphi _p(v) = X_{\mu ^{*}f}(p) = 0$ by Lemma 2.12.
We then deduce the following sufficient conditions for ![]() $M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S, \mathcal {H}}} \mathcal {G}$ to be smooth.
$M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S, \mathcal {H}}} \mathcal {G}$ to be smooth.
Theorem 2.20 (Theorem A(ii))
If ![]() $\mathcal {H}$ acts freely on
$\mathcal {H}$ acts freely on ![]() $N$, then
$N$, then ![]() $S$ is transverse to
$S$ is transverse to ![]() $\mu$. Hence, if the action of
$\mu$. Hence, if the action of ![]() $\mathcal {H}$ on
$\mathcal {H}$ on ![]() $N$ is also proper, then
$N$ is also proper, then ![]() $(S, \mathcal {H})$ is a clean reduction datum and
$(S, \mathcal {H})$ is a clean reduction datum and ![]() $M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S, \mathcal {H}}} \mathcal {G}$ is a symplectic manifold.
$M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S, \mathcal {H}}} \mathcal {G}$ is a symplectic manifold.
Proof. This follows from Proposition 2.19 using the fact that ![]() $\ker (d\varphi _p)_x = 0$ if
$\ker (d\varphi _p)_x = 0$ if ![]() $\mathcal {H}$ acts freely.
$\mathcal {H}$ acts freely.
Recall that the restriction of ![]() $\mathcal {G}$ to
$\mathcal {G}$ to ![]() $S$ is the topological groupoid
$S$ is the topological groupoid
The following criterion will be useful for investigating the properness of the action of ![]() $\mathcal {H}$ on
$\mathcal {H}$ on ![]() $N$.
$N$.
Proposition 2.21 If ![]() $\mathcal {G}$ acts properly on
$\mathcal {G}$ acts properly on ![]() $M$ and
$M$ and ![]() $\mathcal {H}$ is closed in
$\mathcal {H}$ is closed in ![]() $\mathcal {G}\vert _S$, then
$\mathcal {G}\vert _S$, then ![]() $\mathcal {H}$ acts properly on
$\mathcal {H}$ acts properly on ![]() $N$.
$N$.
Proof. As ![]() $\mathcal {H}$ is closed in
$\mathcal {H}$ is closed in ![]() $\mathcal {G}\vert _S$, it suffices to show that the action of
$\mathcal {G}\vert _S$, it suffices to show that the action of ![]() $\mathcal {G}\vert _S$ on
$\mathcal {G}\vert _S$ on ![]() $N$ is proper. By assumption, the map
$N$ is proper. By assumption, the map ![]() $\theta : \mathcal {G}_{\mathsf {t}}{\times }_\mu M \longrightarrow M \times M$ defined by (2.1) is proper.
$\theta : \mathcal {G}_{\mathsf {t}}{\times }_\mu M \longrightarrow M \times M$ defined by (2.1) is proper.
Consider the pullback of ![]() $\theta$ by the inclusion
$\theta$ by the inclusion ![]() $\iota : N \times N \hookrightarrow M \times M$, i.e.
$\iota : N \times N \hookrightarrow M \times M$, i.e.
As ![]() $(\mathcal {G}_{\mathsf {t}}{\times }_\mu M) \times _{M \times M} (N \times N)$ is closed in
$(\mathcal {G}_{\mathsf {t}}{\times }_\mu M) \times _{M \times M} (N \times N)$ is closed in ![]() $(\mathcal {G}_{\mathsf {t}}{\times }_\mu M) \times N \times N$ and
$(\mathcal {G}_{\mathsf {t}}{\times }_\mu M) \times N \times N$ and ![]() $\theta$ is proper, (2.5) is proper. Note that
$\theta$ is proper, (2.5) is proper. Note that
and that (2.5) is the action map ![]() $(\mathcal {G}\vert _N)_{\mathsf {t}}{\times }_\mu N \longrightarrow N \times N$. This shows that the action of
$(\mathcal {G}\vert _N)_{\mathsf {t}}{\times }_\mu N \longrightarrow N \times N$. This shows that the action of ![]() $\mathcal {G}\vert _S$ on
$\mathcal {G}\vert _S$ on ![]() $N$ is proper, as desired.
$N$ is proper, as desired.
Remark 2.22 The stabilizer subgroupoid ![]() $\mathcal {H}$ may not be closed in
$\mathcal {H}$ may not be closed in ![]() $\mathcal {G}\vert _S$, even when
$\mathcal {G}\vert _S$, even when ![]() $S$ is closed in
$S$ is closed in ![]() $X$. See Remark 4.9 for a specific example. This is in contrast to the case of Hamiltonian group actions, where stabilizer subgroups are always closed.
$X$. See Remark 4.9 for a specific example. This is in contrast to the case of Hamiltonian group actions, where stabilizer subgroups are always closed.
2.5 A Poisson map on the reduced space
Let ![]() $\mathcal {G} \rightrightarrows X$ be a symplectic groupoid and
$\mathcal {G} \rightrightarrows X$ be a symplectic groupoid and ![]() $S \subseteq X$ a pre-Poisson submanifold. Note that the distribution on
$S \subseteq X$ a pre-Poisson submanifold. Note that the distribution on ![]() $S$ induced by the orbits of the ssc stabilizer subgroupoid
$S$ induced by the orbits of the ssc stabilizer subgroupoid ![]() $\mathcal {G}_S \rightrightarrows S$ (i.e. the image of the anchor map) is
$\mathcal {G}_S \rightrightarrows S$ (i.e. the image of the anchor map) is ![]() $TS \cap \sigma (TS^{\circ })$. Hence, if
$TS \cap \sigma (TS^{\circ })$. Hence, if ![]() $S / \mathcal {G}_S$ is smooth, it inherits a Poisson structure via Marsden–Ratiu reduction applied to the triple
$S / \mathcal {G}_S$ is smooth, it inherits a Poisson structure via Marsden–Ratiu reduction applied to the triple ![]() $(X, S, \sigma (TS^{\circ }))$ (see [Reference Marsden and RatiuMR86, Example D]). This holds more generally for any stabilizer subgroupoid, as the following proposition shows.
$(X, S, \sigma (TS^{\circ }))$ (see [Reference Marsden and RatiuMR86, Example D]). This holds more generally for any stabilizer subgroupoid, as the following proposition shows.
Proposition 2.23 Consider a symplectic groupoid ![]() $\mathcal {G}\rightrightarrows X$, pre-Poisson submanifold
$\mathcal {G}\rightrightarrows X$, pre-Poisson submanifold ![]() $S \subseteq X$, and stabilizer subgroupoid
$S \subseteq X$, and stabilizer subgroupoid ![]() $\mathcal {H}\rightrightarrows S$ of
$\mathcal {H}\rightrightarrows S$ of ![]() $S$ in
$S$ in ![]() $\mathcal {G}$. Suppose that
$\mathcal {G}$. Suppose that ![]() $S / \mathcal {H}$ has the structure of a smooth manifold such that the quotient map
$S / \mathcal {H}$ has the structure of a smooth manifold such that the quotient map ![]() $\rho : S \longrightarrow S / \mathcal {H}$ is a smooth submersion. Let
$\rho : S \longrightarrow S / \mathcal {H}$ is a smooth submersion. Let ![]() $i : S \longrightarrow X$ be the inclusion map. Then there is a unique Poisson structure on
$i : S \longrightarrow X$ be the inclusion map. Then there is a unique Poisson structure on ![]() $S / \mathcal {H}$ such that for any locally defined smooth functions
$S / \mathcal {H}$ such that for any locally defined smooth functions ![]() $f, g$ on
$f, g$ on ![]() $S / \mathcal {H}$, and locally defined smooth functions
$S / \mathcal {H}$, and locally defined smooth functions ![]() $F, G$ on
$F, G$ on ![]() $X$ such that
$X$ such that ![]() $\rho ^{*}f = i^{*}F$,
$\rho ^{*}f = i^{*}F$, ![]() $\rho ^{*}g = i^{*}G$, and
$\rho ^{*}g = i^{*}G$, and ![]() $dF(\sigma (TS^{\circ })) = dG(\sigma (TS^{\circ })) = 0$, we have
$dF(\sigma (TS^{\circ })) = dG(\sigma (TS^{\circ })) = 0$, we have
Proof. Recall that if ![]() $\mathcal {H}$ is source-connected, then
$\mathcal {H}$ is source-connected, then ![]() $S / \mathcal {H}$ is the Marsden–Ratiu reduction of the triple
$S / \mathcal {H}$ is the Marsden–Ratiu reduction of the triple ![]() $(X, S, \sigma (TS^{\circ }))$ (see [Reference Marsden and RatiuMR86, Example D]). We are thereby reduced to proving the following claim: if
$(X, S, \sigma (TS^{\circ }))$ (see [Reference Marsden and RatiuMR86, Example D]). We are thereby reduced to proving the following claim: if ![]() $f, g, F, G$ are as in the statement, then
$f, g, F, G$ are as in the statement, then ![]() $\{F, G\}_X$ is
$\{F, G\}_X$ is ![]() $\mathcal {H}$-invariant. In other words, we want to show that
$\mathcal {H}$-invariant. In other words, we want to show that ![]() $j^{*}\mathsf {s}^{*}\{F, G\}_X = j^{*}\mathsf {t}^{*}\{F, G\}_X$, where
$j^{*}\mathsf {s}^{*}\{F, G\}_X = j^{*}\mathsf {t}^{*}\{F, G\}_X$, where ![]() $j : \mathcal {H} \longrightarrow \mathcal {G}$ is the immersion of
$j : \mathcal {H} \longrightarrow \mathcal {G}$ is the immersion of ![]() $\mathcal {H}$ in
$\mathcal {H}$ in ![]() $\mathcal {G}$.
$\mathcal {G}$.
Recall from § 2.2 that there is a Poisson transversal ![]() $Y$ in
$Y$ in ![]() $X$ containing
$X$ containing ![]() $S$ as a coisotropic submanifold. The restriction
$S$ as a coisotropic submanifold. The restriction ![]() $\mathcal {G}\vert _Y := \mathsf {s}^{-1}(Y) \cap \mathsf {t}^{-1}(Y)$ is then a symplectic subgroupoid of
$\mathcal {G}\vert _Y := \mathsf {s}^{-1}(Y) \cap \mathsf {t}^{-1}(Y)$ is then a symplectic subgroupoid of ![]() $\mathcal {G}$ (see [Reference Cattaneo and ZambonCZ09, Lemma 7.1]) and
$\mathcal {G}$ (see [Reference Cattaneo and ZambonCZ09, Lemma 7.1]) and ![]() $\mathcal {H}$ is an isotropic Lie subgroupoid of
$\mathcal {H}$ is an isotropic Lie subgroupoid of ![]() $\mathcal {G}\vert _Y$. By [Reference CattaneoCat04, § 5],
$\mathcal {G}\vert _Y$. By [Reference CattaneoCat04, § 5], ![]() $\mathcal {H}$ is Lagrangian in
$\mathcal {H}$ is Lagrangian in ![]() $\mathcal {G}\vert _Y$. We therefore have
$\mathcal {G}\vert _Y$. We therefore have
for all ![]() $h \in \mathcal {H}$, where
$h \in \mathcal {H}$, where ![]() $\Omega$ is the symplectic form on
$\Omega$ is the symplectic form on ![]() $\mathcal {G}$ and
$\mathcal {G}$ and ![]() $T_h\mathcal {H}$ is identified as subspace of
$T_h\mathcal {H}$ is identified as subspace of ![]() $T_{j(h)}\mathcal {G}$ via the immersion
$T_{j(h)}\mathcal {G}$ via the immersion ![]() $j : \mathcal {H} \longrightarrow \mathcal {G}$.
$j : \mathcal {H} \longrightarrow \mathcal {G}$.
As ![]() $TX\vert _Y = TY \oplus \sigma (TY^{\circ })$, there is a locally defined smooth function
$TX\vert _Y = TY \oplus \sigma (TY^{\circ })$, there is a locally defined smooth function ![]() $\tilde {F}$ on
$\tilde {F}$ on ![]() $X$ such that
$X$ such that ![]() $\rho ^{*}f = i^{*}\tilde {F}$ and
$\rho ^{*}f = i^{*}\tilde {F}$ and ![]() $d\tilde {F}(\sigma (TY^{\circ })) = 0$. Note that
$d\tilde {F}(\sigma (TY^{\circ })) = 0$. Note that ![]() $\sigma (T_xS^{\circ }) \cap T_xY \subseteq T_xS$ for all
$\sigma (T_xS^{\circ }) \cap T_xY \subseteq T_xS$ for all ![]() $x \in S$ because
$x \in S$ because ![]() $S$ is coisotropic in
$S$ is coisotropic in ![]() $Y$. We therefore have
$Y$. We therefore have
so ![]() $d\tilde {F}(\sigma (TS^{\circ })) = 0$. On the other hand, we have
$d\tilde {F}(\sigma (TS^{\circ })) = 0$. On the other hand, we have ![]() $i^{*}\{\tilde {F}, G\}_X = i^{*}\{F, G\}_X$ as
$i^{*}\{\tilde {F}, G\}_X = i^{*}\{F, G\}_X$ as ![]() $i^{*}\tilde {F} = i^{*}F$. We may then assume without loss of generality that
$i^{*}\tilde {F} = i^{*}F$. We may then assume without loss of generality that ![]() $dF(\sigma (TY^{\circ })) = 0$, i.e.
$dF(\sigma (TY^{\circ })) = 0$, i.e. ![]() $X_F$ is tangent to
$X_F$ is tangent to ![]() $Y$.
$Y$.
We claim that ![]() $X_{\mathsf {s}^{*}F} - X_{\mathsf {t}^{*}F}$ is tangent to
$X_{\mathsf {s}^{*}F} - X_{\mathsf {t}^{*}F}$ is tangent to ![]() $\mathcal {H}$. A first observation is that
$\mathcal {H}$. A first observation is that ![]() $j^{*}\mathsf {s}^{*}F = j^{*} \mathsf {t}^{*}F$, because
$j^{*}\mathsf {s}^{*}F = j^{*} \mathsf {t}^{*}F$, because
This implies that
so ![]() $X_{\mathsf {s}^{*}F} - X_{\mathsf {t}^{*}F}$ takes values in
$X_{\mathsf {s}^{*}F} - X_{\mathsf {t}^{*}F}$ takes values in ![]() $T\mathcal {H}^{\Omega }$. Now recall that
$T\mathcal {H}^{\Omega }$. Now recall that ![]() $d\mathsf {s}(X_{\mathsf {t}^{*}F}) = 0 = d\mathsf {t}(X_{\mathsf {s}^{*}F})$ (see e.g. [Reference Mikami and WeinsteinMW88, Theorem 1.6(i)]), so
$d\mathsf {s}(X_{\mathsf {t}^{*}F}) = 0 = d\mathsf {t}(X_{\mathsf {s}^{*}F})$ (see e.g. [Reference Mikami and WeinsteinMW88, Theorem 1.6(i)]), so ![]() $d\mathsf {s}(X_{\mathsf {s}^{*}F} - X_{\mathsf {t}^{*}F}) = X_F$ and
$d\mathsf {s}(X_{\mathsf {s}^{*}F} - X_{\mathsf {t}^{*}F}) = X_F$ and ![]() $d\mathsf {t}(X_{\mathsf {s}^{*}F} - X_{\mathsf {t}^{*}F}) = X_F$ are tangent to
$d\mathsf {t}(X_{\mathsf {s}^{*}F} - X_{\mathsf {t}^{*}F}) = X_F$ are tangent to ![]() $Y$. By combining the last two sentences with (2.6), we obtain
$Y$. By combining the last two sentences with (2.6), we obtain
for all ![]() $h \in \mathcal {H}$.
$h \in \mathcal {H}$.
The identity ![]() $j^{*} \mathsf {s}^{*} G = j^{*} \mathsf {t}^{*} G$ therefore implies that for all
$j^{*} \mathsf {s}^{*} G = j^{*} \mathsf {t}^{*} G$ therefore implies that for all ![]() $h \in \mathcal {H}$ and
$h \in \mathcal {H}$ and ![]() $g := j(h)$,
$g := j(h)$,
 \begin{align*} (j^{*}\mathsf{s}^{*}\{F, G\}_X)(h) &= \{\mathsf{s}^{*}F, \mathsf{s}^{*}G\}_X(g) = d(\mathsf{s}^{*}G)(X_{\mathsf{s}^{*}F}|_g) = d(\mathsf{s}^{*}G)(X_{\mathsf{s}^{*}F}|_g - X_{\mathsf{t}^{*}F}|_g) \\ &= d(\mathsf{t}^{*}G)(X_{\mathsf{s}^{*}F}|_g - X_{\mathsf{t}^{*}F}|_g) = -d(\mathsf{t}^{*}G)(X_{\mathsf{t}^{*}F}|_g) = -\{\mathsf{t}^{*}F, \mathsf{t}^{*}G\}(g) \\ &= (j^{*}\mathsf{t}^{*}\{F, G\}_X)(h).\end{align*}
\begin{align*} (j^{*}\mathsf{s}^{*}\{F, G\}_X)(h) &= \{\mathsf{s}^{*}F, \mathsf{s}^{*}G\}_X(g) = d(\mathsf{s}^{*}G)(X_{\mathsf{s}^{*}F}|_g) = d(\mathsf{s}^{*}G)(X_{\mathsf{s}^{*}F}|_g - X_{\mathsf{t}^{*}F}|_g) \\ &= d(\mathsf{t}^{*}G)(X_{\mathsf{s}^{*}F}|_g - X_{\mathsf{t}^{*}F}|_g) = -d(\mathsf{t}^{*}G)(X_{\mathsf{t}^{*}F}|_g) = -\{\mathsf{t}^{*}F, \mathsf{t}^{*}G\}(g) \\ &= (j^{*}\mathsf{t}^{*}\{F, G\}_X)(h).\end{align*}Theorem 2.24 (Theorem A(iii))
Let ![]() $((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$ be a Hamiltonian system and
$((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$ be a Hamiltonian system and ![]() $(S, \mathcal {H})$ a clean reduction datum. Suppose that
$(S, \mathcal {H})$ a clean reduction datum. Suppose that ![]() $S / \mathcal {H}$ has the structure of a smooth manifold such that the quotient map
$S / \mathcal {H}$ has the structure of a smooth manifold such that the quotient map ![]() $S \longrightarrow S / \mathcal {H}$ is a smooth submersion. Then
$S \longrightarrow S / \mathcal {H}$ is a smooth submersion. Then ![]() $\mu : M \longrightarrow X$ descends to a Poisson map
$\mu : M \longrightarrow X$ descends to a Poisson map ![]() $M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S}} \mathcal {G} \longrightarrow S / \mathcal {H}$.
$M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S}} \mathcal {G} \longrightarrow S / \mathcal {H}$.
Proof. Let ![]() $N := \mu ^{-1}(S)$ and consider the following commutative diagram.
$N := \mu ^{-1}(S)$ and consider the following commutative diagram.

Let ![]() $f, g$ be locally defined smooth functions on
$f, g$ be locally defined smooth functions on ![]() $S / \mathcal {H}$ and
$S / \mathcal {H}$ and ![]() $F, G$ local extensions of
$F, G$ local extensions of ![]() $\rho ^{*}f, \rho ^{*}g$ as in Proposition 2.23. We want to show that
$\rho ^{*}f, \rho ^{*}g$ as in Proposition 2.23. We want to show that ![]() $\bar {\mu }^{*}\{f, g\} = \{\bar {\mu }^{*}f, \bar {\mu }^{*}g\}$ or, equivalently,
$\bar {\mu }^{*}\{f, g\} = \{\bar {\mu }^{*}f, \bar {\mu }^{*}g\}$ or, equivalently,
We have
as ![]() $\mu$ is a Poisson map. As the Poisson structure on
$\mu$ is a Poisson map. As the Poisson structure on ![]() $N / \mathcal {H}$ is also obtained from Poisson reduction, it suffices to show the following:
$N / \mathcal {H}$ is also obtained from Poisson reduction, it suffices to show the following:
(1)
 $\mu ^{*}F$ and
$\mu ^{*}F$ and  $\mu ^{*}G$ vanish on
$\mu ^{*}G$ vanish on  $TN^{\omega }$;
$TN^{\omega }$;(2)
 $\mu ^{*}F$ and
$\mu ^{*}F$ and  $\mu ^{*}G$ restrict to
$\mu ^{*}G$ restrict to  $\pi ^{*}\bar {\mu }^{*}f$ and
$\pi ^{*}\bar {\mu }^{*}f$ and  $\pi ^{*}\bar {\mu }^{*}g$ on
$\pi ^{*}\bar {\mu }^{*}g$ on  $N$.
$N$.
To verify part (1), suppose that ![]() $v \in TN^{\omega }$. We have
$v \in TN^{\omega }$. We have ![]() $v = \omega ^{-1}(d\mu ^{*}(\xi ))$ for
$v = \omega ^{-1}(d\mu ^{*}(\xi ))$ for ![]() $\xi \in TS^{\circ }$. As
$\xi \in TS^{\circ }$. As ![]() $\mu$ is Poisson, we obtain
$\mu$ is Poisson, we obtain ![]() $d\mu (v) = \sigma (\xi ) \in \sigma (TS^{\circ })$. It follows that
$d\mu (v) = \sigma (\xi ) \in \sigma (TS^{\circ })$. It follows that ![]() $d(\mu ^{*}F)(v) = dF(d\mu (v)) = 0$. To show part (2), note that
$d(\mu ^{*}F)(v) = dF(d\mu (v)) = 0$. To show part (2), note that ![]() $i^{*}\mu ^{*}F = \tilde {\mu }^{*}j^{*}F = \tilde {\mu }^{*}\rho ^{*}f = \pi ^{*}\bar {\mu }^{*}f$. One has analogous identities for
$i^{*}\mu ^{*}F = \tilde {\mu }^{*}j^{*}F = \tilde {\mu }^{*}\rho ^{*}f = \pi ^{*}\bar {\mu }^{*}f$. One has analogous identities for ![]() $g$ and
$g$ and ![]() $G$.
$G$.
Remark 2.25 If ![]() $TS \cap \sigma (T^{*}X) \subseteq \sigma (TS^{\circ })$, then the Poisson structure on
$TS \cap \sigma (T^{*}X) \subseteq \sigma (TS^{\circ })$, then the Poisson structure on ![]() $S / \mathcal {H}$ is trivial. The Poisson map
$S / \mathcal {H}$ is trivial. The Poisson map ![]() $\overline {\mu }$ then amounts to an ‘integrable system’ on
$\overline {\mu }$ then amounts to an ‘integrable system’ on ![]() $M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S}} \mathcal {G}$.
$M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S}} \mathcal {G}$.
2.6 Examples
Let ![]() $((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$ be a Hamiltonian system. We observe the following special cases of Theorem A.
$((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$ be a Hamiltonian system. We observe the following special cases of Theorem A.
Example 2.26 (Singletons)
If ![]() $S = \{x\}$ is a singleton in
$S = \{x\}$ is a singleton in ![]() $X$, then the isotropy group at
$X$, then the isotropy group at ![]() $x$ is a stabilizer subgroupoid of
$x$ is a stabilizer subgroupoid of ![]() $S$ in
$S$ in ![]() $\mathcal {G}$. We thereby recover Mikami–Weinstein reduction [Reference Mikami and WeinsteinMW88, Theorem 3.12], of which the more classical Marsden–Weinstein–Meyer reduction [Reference MeyerMey73, Reference Marsden and WeinsteinMW74] is a special case.
$\mathcal {G}$. We thereby recover Mikami–Weinstein reduction [Reference Mikami and WeinsteinMW88, Theorem 3.12], of which the more classical Marsden–Weinstein–Meyer reduction [Reference MeyerMey73, Reference Marsden and WeinsteinMW74] is a special case.
Example 2.27 (Poisson transversals)
If ![]() $S \subseteq X$ is Poisson transversal, then
$S \subseteq X$ is Poisson transversal, then ![]() $S$ is transverse to
$S$ is transverse to ![]() $\mu$ (see [Reference Frejlich and MarcutFM17, Lemma 7(1)]). We also have
$\mu$ (see [Reference Frejlich and MarcutFM17, Lemma 7(1)]). We also have ![]() $L_S=0$ in this case, so that the trivial groupoid over
$L_S=0$ in this case, so that the trivial groupoid over ![]() $S$ is a stabilizer subgroupoid. It follows that
$S$ is a stabilizer subgroupoid. It follows that ![]() $M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S}} \mathcal {G} = \mu ^{-1}(S)$, and we recover the fact that
$M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S}} \mathcal {G} = \mu ^{-1}(S)$, and we recover the fact that ![]() $\mu ^{-1}(S)$ is a symplectic submanifold of
$\mu ^{-1}(S)$ is a symplectic submanifold of ![]() $M$.
$M$.
Example 2.28 (General symplectic reduction)
Let ![]() $(M, \omega )$ be a symplectic manifold. The pair groupoid
$(M, \omega )$ be a symplectic manifold. The pair groupoid ![]() $\mathcal {G} := M \times M^{-}$ is then a symplectic groupoid over
$\mathcal {G} := M \times M^{-}$ is then a symplectic groupoid over ![]() $(M, \omega )$, with source map
$(M, \omega )$, with source map ![]() $\mathsf {s}(p, q) = p$, target map
$\mathsf {s}(p, q) = p$, target map ![]() $\mathsf {t}(p, q) = q$, and multiplication
$\mathsf {t}(p, q) = q$, and multiplication ![]() $(p, q)(q, r) = (p, r)$. The symplectic groupoid
$(p, q)(q, r) = (p, r)$. The symplectic groupoid ![]() $\mathcal {G}$ then acts on
$\mathcal {G}$ then acts on ![]() $(M, \omega )$ in a Hamiltonian way with moment map the identity map and action
$(M, \omega )$ in a Hamiltonian way with moment map the identity map and action ![]() $(p, q) \cdot q = p$.
$(p, q) \cdot q = p$.
A submanifold ![]() $i : S \hookrightarrow M$ is pre-Poisson if and only if it is pre-symplectic. In this case, one has
$i : S \hookrightarrow M$ is pre-Poisson if and only if it is pre-symplectic. In this case, one has ![]() $M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S}} \mathcal {G} = S / {\sim }$, where
$M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S}} \mathcal {G} = S / {\sim }$, where ![]() $\sim$ is the equivalence relation generated by the leaves of the distribution
$\sim$ is the equivalence relation generated by the leaves of the distribution ![]() $\ker i^{*}\omega$. We have therefore recovered the procedure of reduction along a pre-symplectic submanifold (Remark 2.18).
$\ker i^{*}\omega$. We have therefore recovered the procedure of reduction along a pre-symplectic submanifold (Remark 2.18).
3. Main construction: complex analytic version
This section is concerned with Theorem B and its proof. We develop a complex analytic version of Marsden–Ratiu reduction [Reference Marsden and RatiuMR86] in § 3.1, and examine its relation to complex pre-Poisson submanifolds in § 3.2. This creates the context needed to prove Theorem B. Parts (i)–(v) of this theorem are proved in § 3.3, whereas parts (vi)–(vii) are proved in § 3.4.
3.1 Complex analytic Marsden–Ratiu reduction
We begin by observing that the notion of Poisson reduction introduced by Marsden–Ratiu [Reference Marsden and RatiuMR86] adapts to the complex analytic setting.
Let us begin with a brief digression on terminology. A holomorphic Poisson structure on a complex analytic space ![]() $(P, \mathcal {O}_P)$ is an enrichment of the structure sheaf
$(P, \mathcal {O}_P)$ is an enrichment of the structure sheaf ![]() $\mathcal {O}_P$ to a sheaf of Poisson algebras. In this case, we call
$\mathcal {O}_P$ to a sheaf of Poisson algebras. In this case, we call ![]() $(P, \mathcal {O}_P)$ a complex analytic Poisson space. We also often identity a Poisson structure with the corresponding homomorphism Poisson bivector field, i.e. the bundle homomorphism
$(P, \mathcal {O}_P)$ a complex analytic Poisson space. We also often identity a Poisson structure with the corresponding homomorphism Poisson bivector field, i.e. the bundle homomorphism
for all ![]() $p \in P$ and
$p \in P$ and ![]() $f \in \mathcal {O}_{P, p}$, where
$f \in \mathcal {O}_{P, p}$, where ![]() $X_f := \{f, \cdot \}$ is the Hamiltonian vector field associated to
$X_f := \{f, \cdot \}$ is the Hamiltonian vector field associated to ![]() $f$. We call
$f$. We call ![]() $P$ symplectic if it is smooth and
$P$ symplectic if it is smooth and ![]() $\tau = \omega ^{-1}$ for some holomorphic symplectic form
$\tau = \omega ^{-1}$ for some holomorphic symplectic form ![]() $\omega : TP \longrightarrow T^{*}P$.
$\omega : TP \longrightarrow T^{*}P$.
Let ![]() $E$ be a holomorphic vector bundle over a complex analytic space
$E$ be a holomorphic vector bundle over a complex analytic space ![]() $P$, and write
$P$, and write ![]() $E_x$ for the fiber of
$E_x$ for the fiber of ![]() $E$ over
$E$ over ![]() $x\in X$. Our convention is that a subbundle of
$x\in X$. Our convention is that a subbundle of ![]() $E$ is simply a complex analytic subspace
$E$ is simply a complex analytic subspace ![]() $R$ of
$R$ of ![]() $E$ whose fibers
$E$ whose fibers ![]() $R_x := R \cap E_x$ are vector subspaces of
$R_x := R \cap E_x$ are vector subspaces of ![]() $E_x$ for all
$E_x$ for all ![]() $x \in P$. Note that the fibers of
$x \in P$. Note that the fibers of ![]() $R$ may have different dimensions, so that
$R$ may have different dimensions, so that ![]() $R$ is not necessarily a vector bundle. For a complex analytic subspace
$R$ is not necessarily a vector bundle. For a complex analytic subspace ![]() $Y \subseteq P$ and a subbundle
$Y \subseteq P$ and a subbundle ![]() $R$ of
$R$ of ![]() $TP\vert _Y$, we write
$TP\vert _Y$, we write ![]() $\mathcal {O}_P^{R}$ for the subsheaf of
$\mathcal {O}_P^{R}$ for the subsheaf of ![]() $\mathcal {O}_P$ defined by
$\mathcal {O}_P$ defined by
for all open subsets ![]() $U \subseteq P$. The germ of a holomorphic function
$U \subseteq P$. The germ of a holomorphic function ![]() $f \in \mathcal {O}_P(U)$ at a point
$f \in \mathcal {O}_P(U)$ at a point ![]() $p \in U$ is denoted
$p \in U$ is denoted ![]() $f_p \in \mathcal {O}_{P, p}$.
$f_p \in \mathcal {O}_{P, p}$.
The following result is a complex analytic analog of [Reference Marsden and RatiuMR86, Theorem 2.2].
Theorem 3.1 (Complex analytic Marsden–Ratiu reduction)
Let ![]() $(M, \tau )$ be a complex analytic Poisson space,
$(M, \tau )$ be a complex analytic Poisson space, ![]() $N \subseteq M$ a reduced complex analytic subspace,
$N \subseteq M$ a reduced complex analytic subspace, ![]() $E \longrightarrow N$ a subbundle of
$E \longrightarrow N$ a subbundle of ![]() $TM\vert _N$, and
$TM\vert _N$, and ![]() $D := TN \cap E$. Suppose that:
$D := TN \cap E$. Suppose that:
(1)
 $\mathcal {O}_M^{E}$ is closed under the Poisson bracket;
$\mathcal {O}_M^{E}$ is closed under the Poisson bracket;(2)
 $\tau (E^{\circ }) \subseteq TN + E$; and
$\tau (E^{\circ }) \subseteq TN + E$; and(3) for all
 $p \in N$ and
$p \in N$ and  $f \in \mathcal {O}_{N, p}^{D}$, there exists
$f \in \mathcal {O}_{N, p}^{D}$, there exists  $F \in \mathcal {O}_{M, p}^{E}$ such that
$F \in \mathcal {O}_{M, p}^{E}$ such that  $F\vert _N = f$.
$F\vert _N = f$.
One then has a unique Poisson bracket ![]() $\{{\cdot }\,{,}\,{\cdot }\}'$ on
$\{{\cdot }\,{,}\,{\cdot }\}'$ on ![]() $\mathcal {O}_N^{D}$ satisfying
$\mathcal {O}_N^{D}$ satisfying
for all ![]() $p \in N$,
$p \in N$, ![]() $f, g \in \mathcal {O}_{N, p}^{D}$, and
$f, g \in \mathcal {O}_{N, p}^{D}$, and ![]() $F, G \in \mathcal {O}_{M, p}^{E}$ related to
$F, G \in \mathcal {O}_{M, p}^{E}$ related to ![]() $f, g$ as in part (3).
$f, g$ as in part (3).
Proof. To see that (3.1) does not depend on the choice of ![]() $F$ and
$F$ and ![]() $G$, we need to show the following: if
$G$, we need to show the following: if ![]() $p \in N$ and
$p \in N$ and ![]() $F, G \in \mathcal {O}_{M, p}^{E}$ are such that
$F, G \in \mathcal {O}_{M, p}^{E}$ are such that ![]() $F\vert _N = 0$, then
$F\vert _N = 0$, then ![]() $\{F, G\}\vert _N = 0$. Note that
$\{F, G\}\vert _N = 0$. Note that ![]() $X_F\vert _N$ takes values in
$X_F\vert _N$ takes values in ![]() $\tau (TN^{\circ } \cap E^{\circ })$, whereas condition (2) implies that
$\tau (TN^{\circ } \cap E^{\circ })$, whereas condition (2) implies that
It follows that ![]() $\tau (TN^{\circ } \cap E^{\circ }) \subseteq E$ and, hence,
$\tau (TN^{\circ } \cap E^{\circ }) \subseteq E$ and, hence, ![]() $\{F, G\}\vert _N = dG(X_F\vert _N) = 0$.
$\{F, G\}\vert _N = dG(X_F\vert _N) = 0$.
Let ![]() $f, g \in \mathcal {O}_N^{D}(U)$ for some open set
$f, g \in \mathcal {O}_N^{D}(U)$ for some open set ![]() $U \subseteq N$. We then get a well-defined element
$U \subseteq N$. We then get a well-defined element ![]() $\{f, g\}' \in \mathcal {O}_N(U)$ defined by the collection of germs
$\{f, g\}' \in \mathcal {O}_N(U)$ defined by the collection of germs ![]() $\{F, G\}\vert _N \in \mathcal {O}_{N, p}$ for all
$\{F, G\}\vert _N \in \mathcal {O}_{N, p}$ for all ![]() $p \in U$ and
$p \in U$ and ![]() $F, G \in \mathcal {O}_{M, p}^{E}$ satisfying
$F, G \in \mathcal {O}_{M, p}^{E}$ satisfying ![]() $F\vert _N = f_p$ and
$F\vert _N = f_p$ and ![]() $G\vert _N = g_p$. We also have
$G\vert _N = g_p$. We also have ![]() $\{f, g\}' \in \mathcal {O}_N^{D}(U)$, because
$\{f, g\}' \in \mathcal {O}_N^{D}(U)$, because
by condition (1).
The Leibniz identity follows from the fact that ![]() $\{f, gh\}' = \{F, GH\}\vert _N$ if
$\{f, gh\}' = \{F, GH\}\vert _N$ if ![]() $f, g, h \in \mathcal {O}_{N, p}$ are related to
$f, g, h \in \mathcal {O}_{N, p}$ are related to ![]() $F, G, H \in \mathcal {O}_{M, p}$ as in condition (3), which holds because
$F, G, H \in \mathcal {O}_{M, p}$ as in condition (3), which holds because ![]() $d(GH)$ also vanishes on
$d(GH)$ also vanishes on ![]() $E$. For the Jacobi identity, note that
$E$. For the Jacobi identity, note that ![]() $\{f, \{g, h\}'\}' = \{F, \{G, H\}\}\vert _N$, because
$\{f, \{g, h\}'\}' = \{F, \{G, H\}\}\vert _N$, because ![]() $\{g, h\}' = \{G, H\}\vert _N$ by definition and
$\{g, h\}' = \{G, H\}\vert _N$ by definition and ![]() $d\{G, H\}(E) = 0$ by condition (1).
$d\{G, H\}(E) = 0$ by condition (1).
Condition (3) is implicit in Marsden–Ratiu reduction [Reference Marsden and RatiuMR86, Theorem 2.2], as it always holds in the context of smooth manifolds. On the other hand, the same argument works for non-singular complex analytic spaces.
Lemma 3.2 Let ![]() $M$ be a complex manifold,
$M$ be a complex manifold, ![]() $N \subseteq M$ a complex submanifold, and
$N \subseteq M$ a complex submanifold, and ![]() $E \longrightarrow N$ a holomorphic subbundle of
$E \longrightarrow N$ a holomorphic subbundle of ![]() $TM\vert _N$. Assume that
$TM\vert _N$. Assume that ![]() $E$ and
$E$ and ![]() $D := TN \cap E$ are vector bundles. For all
$D := TN \cap E$ are vector bundles. For all ![]() $p \in N$ and
$p \in N$ and ![]() $f \in \mathcal {O}_{N, p}^{D}$, there exists
$f \in \mathcal {O}_{N, p}^{D}$, there exists ![]() $F \in \mathcal {O}_{M, p}^{E}$ such that
$F \in \mathcal {O}_{M, p}^{E}$ such that ![]() $F\vert _N = f$.
$F\vert _N = f$.
Proof. Note that this is a local statement. We may therefore assume that ![]() $E = D \oplus R$ for some holomorphic subbundle
$E = D \oplus R$ for some holomorphic subbundle ![]() $R$ of
$R$ of ![]() $TM\vert _N$, and then extend
$TM\vert _N$, and then extend ![]() $R$ to a holomorphic subbundle
$R$ to a holomorphic subbundle ![]() $S$ containing
$S$ containing ![]() $R$ such that
$R$ such that ![]() $TM\vert _N = TN \oplus S$. Then there exists a tubular neighborhood of
$TM\vert _N = TN \oplus S$. Then there exists a tubular neighborhood of ![]() $N$ in
$N$ in ![]() $S$ that is biholomorphic to a neighborhood of
$S$ that is biholomorphic to a neighborhood of ![]() $p$ in
$p$ in ![]() $M$. We may define
$M$. We may define ![]() $F = f \circ \pi$, where
$F = f \circ \pi$, where ![]() $\pi : S \longrightarrow N$ is the bundle map.
$\pi : S \longrightarrow N$ is the bundle map.
The following example of complex analytic Marsden–Ratiu reduction will be important in the remainder of this section.
Proposition 3.3 (Cf. [Reference Marsden and RatiuMR86, Example D])
Let ![]() $(M, \tau )$ be a complex analytic Poisson space,
$(M, \tau )$ be a complex analytic Poisson space, ![]() $N \subseteq M$ a reduced complex analytic subspace, and
$N \subseteq M$ a reduced complex analytic subspace, and ![]() $E := \tau (TN^{\circ })$.
$E := \tau (TN^{\circ })$.
(i) Conditions (1) and (2) in Theorem 3.1 are satisfied.
(ii) If
 $M$ and
$M$ and  $N$ are smooth and
$N$ are smooth and  $E$ and
$E$ and  $D := TN \cap E$ are vector bundles, then condition (3) is also satisfied.
$D := TN \cap E$ are vector bundles, then condition (3) is also satisfied.
Proof. Note that because ![]() $E^{\circ } = \tau (TN^{\circ })^{\circ } = \tau ^{-1}(TN),$ a local holomorphic function
$E^{\circ } = \tau (TN^{\circ })^{\circ } = \tau ^{-1}(TN),$ a local holomorphic function ![]() $F$ on
$F$ on ![]() $M$ satisfies
$M$ satisfies ![]() $dF(E) = 0$ if and only if
$dF(E) = 0$ if and only if ![]() $X_F$ is tangent to
$X_F$ is tangent to ![]() $N$. Condition (1) therefore follows from the Jacobi identity of
$N$. Condition (1) therefore follows from the Jacobi identity of ![]() $\tau$, which is equivalent to
$\tau$, which is equivalent to ![]() $X_{\{F, G\}} = [X_F, X_G]$ for all holomorphic functions
$X_{\{F, G\}} = [X_F, X_G]$ for all holomorphic functions ![]() $F$ and
$F$ and ![]() $G$. Condition (2) also holds because
$G$. Condition (2) also holds because ![]() $\tau (E^{\circ }) = \tau (\tau ^{-1}(TN)) \subseteq TN$. Part (ii) holds by Lemma 3.2.
$\tau (E^{\circ }) = \tau (\tau ^{-1}(TN)) \subseteq TN$. Part (ii) holds by Lemma 3.2.
3.2 Pre-Poisson complex submanifolds
As in § 2, a complex submanifold ![]() $S$ of a holomorphic Poisson manifold
$S$ of a holomorphic Poisson manifold ![]() $(X, \sigma )$ is called pre-Poisson if
$(X, \sigma )$ is called pre-Poisson if ![]() $\sigma ^{-1}(TS) \cap TS^{\circ }$ has constant rank over
$\sigma ^{-1}(TS) \cap TS^{\circ }$ has constant rank over ![]() $S$.
$S$.
We now discuss a special case of complex analytic Marsden–Ratiu reduction (Theorem 3.1) obtained from a Poisson map ![]() $\mu : M \longrightarrow X$ and a pre-Poisson submanifold
$\mu : M \longrightarrow X$ and a pre-Poisson submanifold ![]() $S \subseteq X$. Despite
$S \subseteq X$. Despite ![]() $\mu ^{-1}(S)$ possibly being singular, we show that the conditions of Theorem 3.1 are satisfied with respect to
$\mu ^{-1}(S)$ possibly being singular, we show that the conditions of Theorem 3.1 are satisfied with respect to ![]() $E := \tau (TN^{\circ })$. This will be the basis for our notion of symplectic reduction along a submanifold, where
$E := \tau (TN^{\circ })$. This will be the basis for our notion of symplectic reduction along a submanifold, where ![]() $\mu$ will be the moment map of a Hamiltonian system.
$\mu$ will be the moment map of a Hamiltonian system.
To this end, we first recall some of the results of Cattaneo–Zambon [Reference Cattaneo and ZambonCZ09] and adapt them to the complex analytic setting. Let ![]() $(X, \sigma )$ be a holomorphic Poisson manifold. As in the
$(X, \sigma )$ be a holomorphic Poisson manifold. As in the ![]() $C^{\infty }$ case (§ 2.2), any Poisson transversal complex submanifold
$C^{\infty }$ case (§ 2.2), any Poisson transversal complex submanifold ![]() $Y \subseteq X$ inherits a canonical holomorphic Poisson structure [Reference Frejlich and MarcutFM17, Lemma 3].
$Y \subseteq X$ inherits a canonical holomorphic Poisson structure [Reference Frejlich and MarcutFM17, Lemma 3].
Proposition 3.4 (Cf. [Reference Cattaneo and ZambonCZ09, Theorem 3.3])
Let ![]() $S\subseteq X$ be a pre-Poisson complex submanifold of a holomorphic Poisson manifold
$S\subseteq X$ be a pre-Poisson complex submanifold of a holomorphic Poisson manifold ![]() $(X, \sigma )$. For all
$(X, \sigma )$. For all ![]() $x \in S$, there is a Poisson transversal complex submanifold
$x \in S$, there is a Poisson transversal complex submanifold ![]() $Y \subseteq X$ which contains a neighborhood of
$Y \subseteq X$ which contains a neighborhood of ![]() $x$ in
$x$ in ![]() $S$ as a coisotropic submanifold.
$S$ as a coisotropic submanifold.
Proof. We simply redo the proof of [Reference Cattaneo and ZambonCZ09, Theorem 3.3] locally. Let ![]() $S_x$ be the germ of
$S_x$ be the germ of ![]() $S$ at
$S$ at ![]() $x$. Choose a subbundle
$x$. Choose a subbundle ![]() $R$ of
$R$ of ![]() $TX\vert _{S_x}$ such that
$TX\vert _{S_x}$ such that
and let ![]() $Y$ be a submanifold germ of
$Y$ be a submanifold germ of ![]() $X$ containing
$X$ containing ![]() $S_x$ with
$S_x$ with ![]() $TY\vert _{S_x} = TS_x \oplus R$. Note that the latter is possible because we can choose a tubular neighborhood of
$TY\vert _{S_x} = TS_x \oplus R$. Note that the latter is possible because we can choose a tubular neighborhood of ![]() $S$ near
$S$ near ![]() $x$.
$x$.
Remark 3.5 If ![]() $X$ is Stein and
$X$ is Stein and ![]() $S$ is closed, then there is a Poisson transversal
$S$ is closed, then there is a Poisson transversal ![]() $Y$ containing
$Y$ containing ![]() $S$ globally. To see this, recall that the positive-degree cohomologies of coherent sheaves on Stein manifolds are trivial. Every short exact sequence of vector bundles therefore splits, so that we may choose a global
$S$ globally. To see this, recall that the positive-degree cohomologies of coherent sheaves on Stein manifolds are trivial. Every short exact sequence of vector bundles therefore splits, so that we may choose a global ![]() $R$ in the proof. As the tubular neighborhood theorem holds for Stein manifolds (see e.g. [Reference ForstneričFor17, Theorem 3.3.3]), we can choose a global
$R$ in the proof. As the tubular neighborhood theorem holds for Stein manifolds (see e.g. [Reference ForstneričFor17, Theorem 3.3.3]), we can choose a global ![]() $Y$ with
$Y$ with ![]() $TY\vert _S = TS \oplus R$.
$TY\vert _S = TS \oplus R$.
The previous result is the main ingredient used to obtain condition (3) in complex analytic Marsden–Ratiu reduction.
Proposition 3.6 Let ![]() $\mu : (M, \tau ) \longrightarrow (X, \sigma )$ be a holomorphic Poisson map between holomorphic Poisson manifolds. Let
$\mu : (M, \tau ) \longrightarrow (X, \sigma )$ be a holomorphic Poisson map between holomorphic Poisson manifolds. Let ![]() $S \subseteq X$ be a pre-Poisson complex submanifold such that
$S \subseteq X$ be a pre-Poisson complex submanifold such that ![]() $N := \mu ^{-1}(S)$ is reduced, let
$N := \mu ^{-1}(S)$ is reduced, let ![]() $E := \tau (TN^{\circ })$, and let
$E := \tau (TN^{\circ })$, and let ![]() $D := TN \cap E$. Conditions (1)–(3) in Theorem 3.1 are then satisfied. In particular, for all
$D := TN \cap E$. Conditions (1)–(3) in Theorem 3.1 are then satisfied. In particular, for all ![]() $p \in N$ and
$p \in N$ and ![]() $f \in \mathcal {O}_{N, p}^{D}$, there exists
$f \in \mathcal {O}_{N, p}^{D}$, there exists ![]() $F \in \mathcal {O}_{M, p}^{E}$ such that
$F \in \mathcal {O}_{M, p}^{E}$ such that ![]() $F\vert _N = f$.
$F\vert _N = f$.
Proof. Conditions (1) and (2) hold by Proposition 3.3(i), so it suffices to verify condition (3). We first observe that this third condition is local. Proposition 3.4 therefore allows us to assume that ![]() $S \subseteq Y \subseteq X$, where
$S \subseteq Y \subseteq X$, where ![]() $Y$ is Poisson transversal in
$Y$ is Poisson transversal in ![]() $X$ and
$X$ and ![]() $S$ is coiostropic in
$S$ is coiostropic in ![]() $Y$. By [Reference Frejlich and MarcutFM17, Lemma 7],
$Y$. By [Reference Frejlich and MarcutFM17, Lemma 7], ![]() $Y$ is transverse to
$Y$ is transverse to ![]() $\mu$,
$\mu$, ![]() $P := \mu ^{-1}(Y)$ is a Poisson transversal submanifold of
$P := \mu ^{-1}(Y)$ is a Poisson transversal submanifold of ![]() $M$, and the restriction map
$M$, and the restriction map ![]() $P \longrightarrow Y$ is Poisson.Footnote 4 As the preimage of a coisotropic subspace under a Poisson map is coisotropic,
$P \longrightarrow Y$ is Poisson.Footnote 4 As the preimage of a coisotropic subspace under a Poisson map is coisotropic, ![]() $N=\mu ^{-1}(S)$ is coisotropic in
$N=\mu ^{-1}(S)$ is coisotropic in ![]() $P$.
$P$.
Now let ![]() $p \in N$ and
$p \in N$ and ![]() $f \in \mathcal {O}_{N, p}^{D}$. Extend
$f \in \mathcal {O}_{N, p}^{D}$. Extend ![]() $f$ to
$f$ to ![]() $\tilde {f} \in \mathcal {O}_{P, p}$. As
$\tilde {f} \in \mathcal {O}_{P, p}$. As ![]() $P$ is smooth and
$P$ is smooth and ![]() $TP \cap \tau (TP^{\circ }) = 0$, Lemma 3.2 implies that there exists
$TP \cap \tau (TP^{\circ }) = 0$, Lemma 3.2 implies that there exists ![]() $F \in \mathcal {O}_{M, p}$ such that
$F \in \mathcal {O}_{M, p}$ such that ![]() $F\vert _P = \tilde {f}\vert _P$ and
$F\vert _P = \tilde {f}\vert _P$ and ![]() $dF(\tau (TP^{\circ })) = 0$. We also have that
$dF(\tau (TP^{\circ })) = 0$. We also have that ![]() $TP\vert _N \cap E \subseteq TN$ as
$TP\vert _N \cap E \subseteq TN$ as ![]() $N$ is coisotropic in
$N$ is coisotropic in ![]() $P$, so
$P$, so ![]() $E = D \oplus \tau (TP^{\circ })\vert _N$. It follows that
$E = D \oplus \tau (TP^{\circ })\vert _N$. It follows that
3.3 Complex analytic symplectic reduction along a submanifold
We now state and prove the main result of this section: a complex analytic version of symplectic reduction along a submanifold.
We begin with a few definitions. A holomorphic Hamiltonian system is a tuple ![]() $((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$, where
$((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$, where ![]() $M$ is a complex manifold endowed with a holomorphic symplectic form
$M$ is a complex manifold endowed with a holomorphic symplectic form ![]() $\omega$, and
$\omega$, and ![]() $\mathcal {G} \rightrightarrows X$ is a holomorphic symplectic groupoid acting on
$\mathcal {G} \rightrightarrows X$ is a holomorphic symplectic groupoid acting on ![]() $M$ in a Hamiltonian way with moment map
$M$ in a Hamiltonian way with moment map ![]() $\mu : M \longrightarrow X$; the definition is the same as in § 2, except that ‘smooth’ has become ‘holomorphic’.
$\mu : M \longrightarrow X$; the definition is the same as in § 2, except that ‘smooth’ has become ‘holomorphic’.
In particular, the base ![]() $X$ of a holomorphic Hamiltonian system inherits a canonical holomorphic Poisson bivector field
$X$ of a holomorphic Hamiltonian system inherits a canonical holomorphic Poisson bivector field ![]() $\sigma : T^{*}X \longrightarrow TX$. For a pre-Poisson complex submanifold
$\sigma : T^{*}X \longrightarrow TX$. For a pre-Poisson complex submanifold ![]() $S \subseteq X$, the stabilizer subalgebroid
$S \subseteq X$, the stabilizer subalgebroid
is a holomorphic Lie subalgebroid of ![]() $T^{*}X = \mathrm {Lie}(\mathcal {G})$. By Laurent-Gengoux–Stiénon–Xu's work on the integration of holomorphic Lie algebroids [Reference Laurent-Gengoux, Stiénon and XuLSX09], the source-connected, ssc Lie subgroupoid
$T^{*}X = \mathrm {Lie}(\mathcal {G})$. By Laurent-Gengoux–Stiénon–Xu's work on the integration of holomorphic Lie algebroids [Reference Laurent-Gengoux, Stiénon and XuLSX09], the source-connected, ssc Lie subgroupoid ![]() $\mathcal {G}_S \rightrightarrows S$ of
$\mathcal {G}_S \rightrightarrows S$ of ![]() $\mathcal {G}$ with Lie algebroid
$\mathcal {G}$ with Lie algebroid ![]() $L_S$ is a holomorphic Lie groupoid and the immersion
$L_S$ is a holomorphic Lie groupoid and the immersion ![]() $\mathcal {G}_S \longrightarrow \mathcal {G}$ is holomorphic [Reference Laurent-Gengoux, Stiénon and XuLSX09, Theorem 3.17 and Proposition 3.20]. The subgroupoid
$\mathcal {G}_S \longrightarrow \mathcal {G}$ is holomorphic [Reference Laurent-Gengoux, Stiénon and XuLSX09, Theorem 3.17 and Proposition 3.20]. The subgroupoid ![]() $\mathcal {G}_S$ is also isotropic in
$\mathcal {G}_S$ is also isotropic in ![]() $\mathcal {G}$ by [Reference Cattaneo and ZambonCZ09, Proposition 7.2]. More generally, we call any isotropic holomorphic subgroupoid
$\mathcal {G}$ by [Reference Cattaneo and ZambonCZ09, Proposition 7.2]. More generally, we call any isotropic holomorphic subgroupoid ![]() $\mathcal {H} \rightrightarrows S$ of
$\mathcal {H} \rightrightarrows S$ of ![]() $\mathcal {G}$ with Lie algebroid
$\mathcal {G}$ with Lie algebroid ![]() $L_S$ a holomorphic stabilizer subgroupoid of
$L_S$ a holomorphic stabilizer subgroupoid of ![]() $S$ in
$S$ in ![]() $\mathcal {G}$.
$\mathcal {G}$.
Let ![]() $((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$ be a holomorphic Hamiltonian system,
$((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$ be a holomorphic Hamiltonian system, ![]() $S \subseteq X$ a pre-Poisson complex submanifold, and
$S \subseteq X$ a pre-Poisson complex submanifold, and ![]() $\mathcal {H} \rightrightarrows S$ a holomorphic stabilizer subgroupoid of
$\mathcal {H} \rightrightarrows S$ a holomorphic stabilizer subgroupoid of ![]() $S$ in
$S$ in ![]() $\mathcal {G}$. Let
$\mathcal {G}$. Let ![]() $N := \mu ^{-1}(S) \subseteq M$ be the complex analytic space defined by the ideal generated by all elements
$N := \mu ^{-1}(S) \subseteq M$ be the complex analytic space defined by the ideal generated by all elements ![]() $\mu ^{*}f$, where
$\mu ^{*}f$, where ![]() $f$ is in the ideal of
$f$ is in the ideal of ![]() $S\subseteq X$. One then has a holomorphic action of
$S\subseteq X$. One then has a holomorphic action of ![]() $\mathcal {H} \rightrightarrows S$ on
$\mathcal {H} \rightrightarrows S$ on ![]() $N$. Given any point
$N$. Given any point ![]() $p \in N$, we have a holomorphic orbit map
$p \in N$, we have a holomorphic orbit map
This enables us to define
as a vector subspace of ![]() $T_pN$.
$T_pN$.
Proposition 3.7 We have
for all ![]() $p \in N$.
$p \in N$.
Proof. By the definition of ![]() $N$, we have
$N$, we have ![]() $T_pN = d\mu _p^{-1}(T_{\mu (p)}S)$. This allows us to repeat the proof of Theorem 2.10 verbatim in the present context.
$T_pN = d\mu _p^{-1}(T_{\mu (p)}S)$. This allows us to repeat the proof of Theorem 2.10 verbatim in the present context.
For an ![]() $\mathcal {H}$-invariant open subset
$\mathcal {H}$-invariant open subset ![]() $U \subseteq N$, we let
$U \subseteq N$, we let ![]() $\mathcal {O}_N(U)^{\mathcal{H}}$ be the set of
$\mathcal {O}_N(U)^{\mathcal{H}}$ be the set of ![]() $\mathcal {H}$-invariant elements of
$\mathcal {H}$-invariant elements of ![]() $\mathcal {O}_N(U)$. The next result gives a Poisson structure on
$\mathcal {O}_N(U)$. The next result gives a Poisson structure on ![]() $\mathcal {O}_N(U)^{\mathcal{H}}$; it is the first step towards the construction of a Poisson structure on a quotient of
$\mathcal {O}_N(U)^{\mathcal{H}}$; it is the first step towards the construction of a Poisson structure on a quotient of ![]() $N$ by
$N$ by ![]() $\mathcal {H}$.
$\mathcal {H}$.
Theorem 3.8 Let ![]() $((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$ be a holomorphic Hamiltonian system,
$((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$ be a holomorphic Hamiltonian system, ![]() $S \subseteq X$ a pre-Poisson complex submanifold such that
$S \subseteq X$ a pre-Poisson complex submanifold such that ![]() $N := \mu ^{-1}(S)$ is reduced, and
$N := \mu ^{-1}(S)$ is reduced, and ![]() $\mathcal {H} \rightrightarrows S$ a holomorphic stabilizer subgroupoid of
$\mathcal {H} \rightrightarrows S$ a holomorphic stabilizer subgroupoid of ![]() $S$ in
$S$ in ![]() $\mathcal {G}$. For every
$\mathcal {G}$. For every ![]() $\mathcal {H}$-invariant open set
$\mathcal {H}$-invariant open set ![]() $U \subseteq N$, there is a unique Poisson bracket
$U \subseteq N$, there is a unique Poisson bracket
with the following property: for all ![]() $f, g \in \mathcal {O}_N(U)^{\mathcal{H}}$ and
$f, g \in \mathcal {O}_N(U)^{\mathcal{H}}$ and ![]() $p \in U$, the germ of
$p \in U$, the germ of ![]() $\{f, g\}'$ at
$\{f, g\}'$ at ![]() $p$ is
$p$ is ![]() $\{F, G\}\vert _N$, where
$\{F, G\}\vert _N$, where ![]() $F, G \in \mathcal {O}_{M, p}$ are any extensions of the germs of
$F, G \in \mathcal {O}_{M, p}$ are any extensions of the germs of ![]() $f, g$ at
$f, g$ at ![]() $p$ such that
$p$ such that ![]() $dF(TN^{\omega }) = dG(TN^{\omega }) = 0$.
$dF(TN^{\omega }) = dG(TN^{\omega }) = 0$.
Proof. Proposition 3.7 implies that ![]() $\mathcal {O}_N(U)^{\mathcal{H}} \subseteq \mathcal {O}_N^{D}(U)$, where
$\mathcal {O}_N(U)^{\mathcal{H}} \subseteq \mathcal {O}_N^{D}(U)$, where ![]() $D := TN \cap TN^{\omega }$. As the moment map
$D := TN \cap TN^{\omega }$. As the moment map ![]() $\mu : M \longrightarrow X$ is Poisson, Proposition 3.6 shows that the complex analytic version of the Marsden–Ratiu theorem (Theorem 3.1) holds, producing a Poisson bracket
$\mu : M \longrightarrow X$ is Poisson, Proposition 3.6 shows that the complex analytic version of the Marsden–Ratiu theorem (Theorem 3.1) holds, producing a Poisson bracket
It suffices to show that ![]() $\mathcal {O}_N(U)^{\mathcal{H}}$ is closed under
$\mathcal {O}_N(U)^{\mathcal{H}}$ is closed under ![]() $\{{\cdot }\,{,}\,{\cdot }\}'$.
$\{{\cdot }\,{,}\,{\cdot }\}'$.
Let ![]() $f, g \in \mathcal {O}_N(U)^{\mathcal{H}}$, let
$f, g \in \mathcal {O}_N(U)^{\mathcal{H}}$, let ![]() $p \in U$, and let
$p \in U$, and let ![]() $h \in \mathcal {H}$ be such that
$h \in \mathcal {H}$ be such that ![]() $\mathsf {t}(h) = \mu (p)$. We want to show that
$\mathsf {t}(h) = \mu (p)$. We want to show that
In other words, we want to show that for any ![]() $F, G \in \mathcal {O}_{M, p}^{TN^{\omega }}$ satisfying
$F, G \in \mathcal {O}_{M, p}^{TN^{\omega }}$ satisfying ![]() $F\vert _N = f_p$,
$F\vert _N = f_p$, ![]() $G\vert _N = g_p$, and any
$G\vert _N = g_p$, and any ![]() $\tilde {F}, \tilde {G} \in \mathcal {O}_{M, h \cdot p}^{TN^{\omega }}$ satisfying
$\tilde {F}, \tilde {G} \in \mathcal {O}_{M, h \cdot p}^{TN^{\omega }}$ satisfying ![]() $\tilde {F}\vert _N = f_{h \cdot p}$,
$\tilde {F}\vert _N = f_{h \cdot p}$, ![]() $\tilde {G}\vert _N = g_{h \cdot p}$, we have
$\tilde {G}\vert _N = g_{h \cdot p}$, we have
As ![]() $\mathsf {t}$ is a submersion, we can find a local holomorphic section
$\mathsf {t}$ is a submersion, we can find a local holomorphic section
of ![]() $\mathsf {t}$ passing through
$\mathsf {t}$ passing through ![]() $h$, i.e.
$h$, i.e. ![]() $V$ is a neighborhood of
$V$ is a neighborhood of ![]() $\mathsf {t}(h)$ in
$\mathsf {t}(h)$ in ![]() $S$,
$S$, ![]() $\mathsf {t} \circ \rho = \mathrm {Id}$, and
$\mathsf {t} \circ \rho = \mathrm {Id}$, and ![]() $\rho (\mathsf {t}(h)) = h$. We then get a biholomorphism
$\rho (\mathsf {t}(h)) = h$. We then get a biholomorphism
such that ![]() $\psi _\rho (p) = h \cdot p$.
$\psi _\rho (p) = h \cdot p$.
To show (3.2), we first claim that
where ![]() $i : N \longrightarrow M$ is the inclusion map. Note that for all
$i : N \longrightarrow M$ is the inclusion map. Note that for all ![]() $q \in N \cap \mu ^{-1}(V)$,
$q \in N \cap \mu ^{-1}(V)$, ![]() $(\rho (\mu (q)), q, \psi _\rho (q))$ is in the graph
$(\rho (\mu (q)), q, \psi _\rho (q))$ is in the graph ![]() $\Gamma$ of the action of
$\Gamma$ of the action of ![]() $\mathcal {G}$ on
$\mathcal {G}$ on ![]() $M$, which is Lagrangian in
$M$, which is Lagrangian in ![]() $\mathcal {G} \times M \times M^{-}$ by definition.Footnote 5 Hence, for all
$\mathcal {G} \times M \times M^{-}$ by definition.Footnote 5 Hence, for all ![]() $u, v \in T_qN$, we have
$u, v \in T_qN$, we have
and the analogous statement is true for ![]() $v$. It follows that
$v$. It follows that
However, ![]() $\mathcal {H}$ is isotropic in
$\mathcal {H}$ is isotropic in ![]() $\mathcal {G}$, so the first term vanishes. This proves (3.3).
$\mathcal {G}$, so the first term vanishes. This proves (3.3).
Now note that ![]() $X_F$ and
$X_F$ and ![]() $X_G$ are tangent to
$X_G$ are tangent to ![]() $N$, as one has
$N$, as one has
and an analogous statement for ![]() $X_G$. In particular, we may evaluate
$X_G$. In particular, we may evaluate ![]() $d\psi _\rho$ at
$d\psi _\rho$ at ![]() $X_F|_p$. We claim that
$X_F|_p$. We claim that
To see this, let ![]() $v \in T_{\psi _\rho (p)}N$ and write
$v \in T_{\psi _\rho (p)}N$ and write ![]() $v = d\psi _\rho (u)$ for
$v = d\psi _\rho (u)$ for ![]() $u \in T_pN$. Then by (3.3), we have
$u \in T_pN$. Then by (3.3), we have
However, ![]() $f$ is
$f$ is ![]() $\mathcal {H}$-invariant, so
$\mathcal {H}$-invariant, so
This proves (3.4).
At the same time, because ![]() $d\tilde {G}(TN^{\omega }) = 0$, (3.4) shows that
$d\tilde {G}(TN^{\omega }) = 0$, (3.4) shows that
 \begin{align*} \{\tilde{F}, \tilde{G}\}(h \cdot p) &= d\tilde{G}(X_{\tilde{F}}|_{h \cdot p}) = d\tilde{G}(d\psi_\rho(X_F|_p)) = dg(d\psi_\rho(X_F|_p)) = dg(X_F|_p) = dG(X_F|_p)\\ &= \{F, G\}(p). \end{align*}
\begin{align*} \{\tilde{F}, \tilde{G}\}(h \cdot p) &= d\tilde{G}(X_{\tilde{F}}|_{h \cdot p}) = d\tilde{G}(d\psi_\rho(X_F|_p)) = dg(d\psi_\rho(X_F|_p)) = dg(X_F|_p) = dG(X_F|_p)\\ &= \{F, G\}(p). \end{align*}
This proves (3.2) and, hence, ![]() $\mathcal {O}_N(U)^{\mathcal{H}}$ is closed under
$\mathcal {O}_N(U)^{\mathcal{H}}$ is closed under ![]() $\{{\cdot }\,{,}\,{\cdot }\}'$.
$\{{\cdot }\,{,}\,{\cdot }\}'$.
To discuss the quotient of ![]() $N$ by
$N$ by ![]() $\mathcal {H}$ in the most general context, we make the following definition.
$\mathcal {H}$ in the most general context, we make the following definition.
Definition 3.9 Let ![]() $\mathcal {H}$ be a holomorphic Lie groupoid acting holomorphically on a complex analytic space
$\mathcal {H}$ be a holomorphic Lie groupoid acting holomorphically on a complex analytic space ![]() $(N, \mathcal {O}_N)$. A complex analytic quotient of
$(N, \mathcal {O}_N)$. A complex analytic quotient of ![]() $N$ by
$N$ by ![]() $\mathcal {H}$ is a complex analytic space
$\mathcal {H}$ is a complex analytic space ![]() $(Q, \mathcal {O}_Q)$ together with an
$(Q, \mathcal {O}_Q)$ together with an ![]() $\mathcal {H}$-invariant holomorphic map
$\mathcal {H}$-invariant holomorphic map ![]() $\pi : N \longrightarrow Q$ such that
$\pi : N \longrightarrow Q$ such that
is a sheaf isomorphism.
Theorem 3.8 then has the following consequence.
Theorem 3.10 (Theorem B(i)–(iv))
Let ![]() $((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$ be a holomorphic Hamiltonian system,
$((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$ be a holomorphic Hamiltonian system, ![]() $S \subseteq X$ a pre-Poisson complex submanifold, and
$S \subseteq X$ a pre-Poisson complex submanifold, and ![]() $\mathcal {H} \rightrightarrows S$ a holomorphic stabilizer subgroupoid of
$\mathcal {H} \rightrightarrows S$ a holomorphic stabilizer subgroupoid of ![]() $S$ in
$S$ in ![]() $\mathcal {G}$. Suppose that
$\mathcal {G}$. Suppose that ![]() $N := \mu ^{-1}(S)$ is reduced and that there is a complex analytic quotient of
$N := \mu ^{-1}(S)$ is reduced and that there is a complex analytic quotient of ![]() $N$ by
$N$ by ![]() $\mathcal {H}$, denoted
$\mathcal {H}$, denoted ![]() $\pi : N \longrightarrow Q$.
$\pi : N \longrightarrow Q$.
(i) For all
 $p \in N$ and
$p \in N$ and  $f \in \mathcal {O}_{Q, \pi (p)}$, there exists
$f \in \mathcal {O}_{Q, \pi (p)}$, there exists  $F \in \mathcal {O}_{M, p}$ such that
$F \in \mathcal {O}_{M, p}$ such that  $\pi ^{*}f = F\vert _N \in \mathcal {O}_{N, p}$ and
$\pi ^{*}f = F\vert _N \in \mathcal {O}_{N, p}$ and  $dF(TN^{\omega }) = 0$.
$dF(TN^{\omega }) = 0$.(ii) There is a unique holomorphic Poisson structure
 $\{{\cdot }\,{,}\,{\cdot }\}_Q$ on
$\{{\cdot }\,{,}\,{\cdot }\}_Q$ on  $Q$ such that
for all
$Q$ such that
for all \begin{align*} \pi^{*}\{f, g\}_Q = \{F, G\}_M\vert_N \end{align*}
\begin{align*} \pi^{*}\{f, g\}_Q = \{F, G\}_M\vert_N \end{align*} $f, g \in \mathcal {O}_{Q, \pi (p)}$ and
$f, g \in \mathcal {O}_{Q, \pi (p)}$ and  $F, G \in \mathcal {O}_{M, p}$ related to
$F, G \in \mathcal {O}_{M, p}$ related to  $f, g$ as in part (i).
$f, g$ as in part (i).(iii) Assume that there exists
 $p \in N$ such that
$p \in N$ such that  $d\pi _p$ is surjective,
$d\pi _p$ is surjective,  $\pi ^{-1}(\pi (p))$ is an
$\pi ^{-1}(\pi (p))$ is an  $\mathcal {H}$-orbit, and
$\mathcal {H}$-orbit, and  $\pi (p)$ is a smooth point of
$\pi (p)$ is a smooth point of  $Q$. The Poisson structure in part (ii) is then symplectic on a neighborhood of
$Q$. The Poisson structure in part (ii) is then symplectic on a neighborhood of  $\pi (p)$.
$\pi (p)$.(iv) Suppose that
 $S$ intersects
$S$ intersects  $\mu$ cleanly and that
$\mu$ cleanly and that  $Q = N/\mathcal {H}$ has a complex-manifold structure such that
$Q = N/\mathcal {H}$ has a complex-manifold structure such that  $\pi : N \longrightarrow Q$ is a holomorphic submersion. The Poisson structure on
$\pi : N \longrightarrow Q$ is a holomorphic submersion. The Poisson structure on  $Q$ is then induced by a holomorphic symplectic form
$Q$ is then induced by a holomorphic symplectic form  $\bar {\omega }$ satisfying
$\bar {\omega }$ satisfying  $\pi ^{*}\bar {\omega } = i^{*}\omega$, where
$\pi ^{*}\bar {\omega } = i^{*}\omega$, where  $i : N\longrightarrow M$ is the inclusion map.
$i : N\longrightarrow M$ is the inclusion map.
Proof. Part (i) follows from Proposition 3.6 and part (ii) follows from Theorem 3.8 using the isomorphisms ![]() $\pi ^{*} : \mathcal {O}_Q(U) \cong \mathcal {O}_N(\pi ^{-1}(U))^{\mathcal{H}}$.
$\pi ^{*} : \mathcal {O}_Q(U) \cong \mathcal {O}_N(\pi ^{-1}(U))^{\mathcal{H}}$.
To prove part (iii), let ![]() $x := \pi (p)$ and let
$x := \pi (p)$ and let ![]() $\tau : T_x^{*}Q \longrightarrow T_xQ$ be the Poisson structure at
$\tau : T_x^{*}Q \longrightarrow T_xQ$ be the Poisson structure at ![]() $x$. It suffices to show that
$x$. It suffices to show that ![]() $\tau$ has an inverse
$\tau$ has an inverse ![]() $\bar {\omega }_x : T_xQ \longrightarrow T_x^{*}Q$.
$\bar {\omega }_x : T_xQ \longrightarrow T_x^{*}Q$.
As ![]() $\pi ^{-1}(x) = \mathcal {H} \cdot p$, Proposition 3.7 shows that
$\pi ^{-1}(x) = \mathcal {H} \cdot p$, Proposition 3.7 shows that ![]() $\ker d\pi _p = T_pN \cap T_pN^{\omega }$, so we have a short exact sequence
$\ker d\pi _p = T_pN \cap T_pN^{\omega }$, so we have a short exact sequence
It follows that the symplectic form ![]() $\omega _x : T_xM \longrightarrow T_x^{*}M$ descends to a map
$\omega _x : T_xM \longrightarrow T_x^{*}M$ descends to a map ![]() $\bar {\omega }_x : T_xQ \longrightarrow T_x^{*}Q$. To show that
$\bar {\omega }_x : T_xQ \longrightarrow T_x^{*}Q$. To show that ![]() $\bar {\omega }_x$ is an inverse of
$\bar {\omega }_x$ is an inverse of ![]() $\tau$, let
$\tau$, let ![]() $f \in \mathcal {O}_{Q, x}$ and
$f \in \mathcal {O}_{Q, x}$ and ![]() $F \in \mathcal {O}_{M, p}$ be such that
$F \in \mathcal {O}_{M, p}$ be such that ![]() $\pi ^{*}f = F\vert _N$ and
$\pi ^{*}f = F\vert _N$ and ![]() $dF(TN^{\omega }) = 0$. By the definition of
$dF(TN^{\omega }) = 0$. By the definition of ![]() $\tau$, we have
$\tau$, we have ![]() $\tau (df_x) = d\pi (X_F|_p)$. Hence, for all
$\tau (df_x) = d\pi (X_F|_p)$. Hence, for all ![]() $v \in T_pN$, we have
$v \in T_pN$, we have
This shows that ![]() $\bar {\omega }_x \circ \tau = \mathrm {Id}$, so that
$\bar {\omega }_x \circ \tau = \mathrm {Id}$, so that ![]() $\bar {\omega }_x$ is indeed an inverse of
$\bar {\omega }_x$ is indeed an inverse of ![]() $\tau$.
$\tau$.
Part (iv) follows immediately from part (iii).
Definition 3.11 The complex analytic Poisson space ![]() $(Q, \mathcal {O}_Q)$ in Theorem 3.10 is called the symplectic reduction of
$(Q, \mathcal {O}_Q)$ in Theorem 3.10 is called the symplectic reduction of ![]() $M$ by
$M$ by ![]() $\mathcal {G}$ along
$\mathcal {G}$ along ![]() $S$ with respect to
$S$ with respect to ![]() $\mathcal {H}$ and
$\mathcal {H}$ and ![]() $\pi$ and denoted
$\pi$ and denoted ![]() $M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S, \mathcal {H}, \pi }} \mathcal {G}$. The pair
$M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S, \mathcal {H}, \pi }} \mathcal {G}$. The pair ![]() $(S, \mathcal {H})$ is called a reduction datum; it is called a clean reduction datum if the conditions of Theorem 3.10(iv) are satisfied, in which case
$(S, \mathcal {H})$ is called a reduction datum; it is called a clean reduction datum if the conditions of Theorem 3.10(iv) are satisfied, in which case
is a complex symplectic manifold. If ![]() $(S, \mathcal {H})$ is clean and
$(S, \mathcal {H})$ is clean and ![]() $\mathcal {H}$ is source-connected, we use the simplified notation
$\mathcal {H}$ is source-connected, we use the simplified notation
and call it the symplectic reduction of ![]() $M$ by
$M$ by ![]() $\mathcal {G}$ along
$\mathcal {G}$ along ![]() $S$.
$S$.
Remark 3.12 We remind the reader that any two choices of source-connected stabilizer subgroupoid ![]() $\mathcal {H}\rightrightarrows S$ yield the same reduced space
$\mathcal {H}\rightrightarrows S$ yield the same reduced space ![]() $M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S, \mathcal {H}}} \mathcal {G}$. This justifies our notation
$M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S, \mathcal {H}}} \mathcal {G}$. This justifies our notation ![]() ${M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S}} \mathcal {G}}$.
${M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S}} \mathcal {G}}$.
Remark 3.13 The reducedness assumption on ![]() $N$ is not always satisfied. To see this, consider the standard representation of
$N$ is not always satisfied. To see this, consider the standard representation of ![]() $\mathrm {SL}(2, \mathbb {C})$ on
$\mathrm {SL}(2, \mathbb {C})$ on ![]() $\mathbb {C}^{2}$ and its lift to a Hamiltonian action on
$\mathbb {C}^{2}$ and its lift to a Hamiltonian action on ![]() $T^{*}\mathbb {C}^{2} = \mathbb {C}^{4}$. In coordinates
$T^{*}\mathbb {C}^{2} = \mathbb {C}^{4}$. In coordinates ![]() $(z_1, z_2, w_1, w_2)$, the components of the moment map are
$(z_1, z_2, w_1, w_2)$, the components of the moment map are ![]() $\mu _1 = z_1 w_2$,
$\mu _1 = z_1 w_2$, ![]() $\mu _2 = z_2 w_1$, and
$\mu _2 = z_2 w_1$, and ![]() $\mu _3 = z_1 w_1 - z_2 w_2$ (see e.g. [Reference Herbig, Schwarz and SeatonHSS20, Example 2.6]). Note that
$\mu _3 = z_1 w_1 - z_2 w_2$ (see e.g. [Reference Herbig, Schwarz and SeatonHSS20, Example 2.6]). Note that ![]() $f := z_1w_1 + z_2w_2$ is not in the ideal generated by
$f := z_1w_1 + z_2w_2$ is not in the ideal generated by ![]() $\mu$, but that
$\mu$, but that ![]() $f^{2} = \mu _3^{2} + 4\mu _1\mu _2$ belongs to this ideal.
$f^{2} = \mu _3^{2} + 4\mu _1\mu _2$ belongs to this ideal.
The next result shows that the sufficient condition for smoothness discussed in § 2.4 adapts to the complex analytic setting.
Proposition 3.14 (Theorem B(v))
Let ![]() $((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$ be a holomorphic Hamiltonian system,
$((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$ be a holomorphic Hamiltonian system, ![]() $S \subseteq X$ a pre-Poisson complex submanifold, and
$S \subseteq X$ a pre-Poisson complex submanifold, and ![]() $\mathcal {H} \rightrightarrows S$ a holomorphic stabilizer subgroupoid of
$\mathcal {H} \rightrightarrows S$ a holomorphic stabilizer subgroupoid of ![]() $S$ in
$S$ in ![]() $\mathcal {G}$. If
$\mathcal {G}$. If ![]() $\mathcal {H}$ acts freely on
$\mathcal {H}$ acts freely on ![]() $N := \mu ^{-1}(S)$, then
$N := \mu ^{-1}(S)$, then ![]() $S$ is transverse to
$S$ is transverse to ![]() $\mu$. If the
$\mu$. If the ![]() $\mathcal {H}$-action is also proper, then
$\mathcal {H}$-action is also proper, then ![]() $(S, \mathcal {H})$ is a clean reduction datum and
$(S, \mathcal {H})$ is a clean reduction datum and ![]() $M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S, \mathcal {H}}} \mathcal {G}$ is a complex symplectic manifold.
$M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S, \mathcal {H}}} \mathcal {G}$ is a complex symplectic manifold.
Proof. The proof of Theorem 2.20 adapts to the complex analytic category, showing that ![]() $S$ is transverse to
$S$ is transverse to ![]() $\mu$. Hence,
$\mu$. Hence, ![]() $N$ is a complex submanifold of
$N$ is a complex submanifold of ![]() $M$ on which
$M$ on which ![]() $\mathcal {H}$ acts freely and properly. By Godement's criterion (see e.g. [Reference SerreSer92, Part II, Chapter III, Theorem 2 on p. 92]),
$\mathcal {H}$ acts freely and properly. By Godement's criterion (see e.g. [Reference SerreSer92, Part II, Chapter III, Theorem 2 on p. 92]), ![]() $N / \mathcal {H}$ has a unique complex manifold structure such that the quotient map
$N / \mathcal {H}$ has a unique complex manifold structure such that the quotient map ![]() $\pi : N \longrightarrow N / \mathcal {H}$ is a holomorphic submersion. This shows that
$\pi : N \longrightarrow N / \mathcal {H}$ is a holomorphic submersion. This shows that ![]() $(S, \mathcal {H})$ is a clean reduction datum. We may therefore apply Theorem 3.10(iv) to complete the proof.
$(S, \mathcal {H})$ is a clean reduction datum. We may therefore apply Theorem 3.10(iv) to complete the proof.
3.4 A Poisson map on the reduced space
We now discuss a complex analytic version of Theorem A(iii). To this end, we first discuss the existence of a Poisson structure on a complex analytic quotient of ![]() $S$ by
$S$ by ![]() $\mathcal {H}$.
$\mathcal {H}$.
Proposition 3.15 (Theorem B(vi))
Let ![]() $\mathcal {G} \rightrightarrows X$ be a holomorphic symplectic groupoid,
$\mathcal {G} \rightrightarrows X$ be a holomorphic symplectic groupoid, ![]() $S \subseteq X$ a pre-Poisson complex submanifold, and
$S \subseteq X$ a pre-Poisson complex submanifold, and ![]() $\mathcal {H} \rightrightarrows S$ a holomorphic stabilizer subgroupoid of
$\mathcal {H} \rightrightarrows S$ a holomorphic stabilizer subgroupoid of ![]() $S$ in
$S$ in ![]() $\mathcal {G}$. Suppose that there is a complex analytic quotient of
$\mathcal {G}$. Suppose that there is a complex analytic quotient of ![]() $S$ by
$S$ by ![]() $\mathcal {H}$, denoted
$\mathcal {H}$, denoted ![]() $\rho : S \longrightarrow R$. Then there is a unique holomorphic Poisson structure on
$\rho : S \longrightarrow R$. Then there is a unique holomorphic Poisson structure on ![]() $R$ such that
$R$ such that
for all ![]() $x \in S$,
$x \in S$, ![]() $f, g \in \mathcal {O}_{R, \rho (x)}$, and
$f, g \in \mathcal {O}_{R, \rho (x)}$, and ![]() $F, G \in \mathcal {O}_{X, x}^{\sigma (TS^{\circ })}$ satisfying
$F, G \in \mathcal {O}_{X, x}^{\sigma (TS^{\circ })}$ satisfying ![]() $\rho ^{*}f = F\vert _S$,
$\rho ^{*}f = F\vert _S$, ![]() $\rho ^{*}g = G\vert _S$.
$\rho ^{*}g = G\vert _S$.
Proof. Proposition 3.6 gives us a Poisson bracket on ![]() $\mathcal {O}_S^{D}$, where
$\mathcal {O}_S^{D}$, where ![]() $D := TS \cap \sigma (TS^{\circ })$. To show that this gives a Poisson bracket on
$D := TS \cap \sigma (TS^{\circ })$. To show that this gives a Poisson bracket on ![]() $\mathcal {O}_{R} = (\rho _*\mathcal {O}_S)^{\mathcal{H}}$, it suffices to show that
$\mathcal {O}_{R} = (\rho _*\mathcal {O}_S)^{\mathcal{H}}$, it suffices to show that ![]() $\mathcal {H}$-invariant functions in
$\mathcal {H}$-invariant functions in ![]() $\mathcal {O}_S^{D}$ are closed under the Poisson bracket. This follows from the same reasoning as in the proof of Proposition 2.23, using Proposition 3.4 in the present case.
$\mathcal {O}_S^{D}$ are closed under the Poisson bracket. This follows from the same reasoning as in the proof of Proposition 2.23, using Proposition 3.4 in the present case.
Theorem 3.16 (Theorem B(vii))
Let ![]() $((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$ be a holomorphic Hamiltonian system,
$((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$ be a holomorphic Hamiltonian system, ![]() $S \subseteq X$ a complex pre-Poisson submanifold, and
$S \subseteq X$ a complex pre-Poisson submanifold, and ![]() $\mathcal {H} \rightrightarrows S$ a holomorphic stabilizer subgroupoid of
$\mathcal {H} \rightrightarrows S$ a holomorphic stabilizer subgroupoid of ![]() $S$ in
$S$ in ![]() $\mathcal {G}$. Suppose that
$\mathcal {G}$. Suppose that ![]() $N := \mu ^{-1}(S)$ is reduced and that there is a complex analytic quotient
$N := \mu ^{-1}(S)$ is reduced and that there is a complex analytic quotient ![]() $\pi : N \longrightarrow M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S, \mathcal {H}, \pi }} \mathcal {H}$ of
$\pi : N \longrightarrow M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S, \mathcal {H}, \pi }} \mathcal {H}$ of ![]() $N$ by
$N$ by ![]() $\mathcal {H}$. Let us also suppose that there is a complex analytic quotient
$\mathcal {H}$. Let us also suppose that there is a complex analytic quotient ![]() $\rho : S \longrightarrow R$ of
$\rho : S \longrightarrow R$ of ![]() $S$ by
$S$ by ![]() $\mathcal {H}$, and that the moment map
$\mathcal {H}$, and that the moment map ![]() $\mu : M \longrightarrow X$ descends to a holomorphic map
$\mu : M \longrightarrow X$ descends to a holomorphic map
Then ![]() $\bar {\mu }$ is a Poisson map with respect to the Poisson structures of Theorem 3.10 and Proposition 3.15.
$\bar {\mu }$ is a Poisson map with respect to the Poisson structures of Theorem 3.10 and Proposition 3.15.
Proof. This follows from the definitions of the Poisson structures using the same reasoning as in the proof of Theorem 2.24.
4. Symplectic reduction by a Lie group along a submanifold
This section examines the implications of §§ 2 and 3 for classical Hamiltonian ![]() $G$-spaces. In § 4.1, we derive some of the Lie-theoretic machinery relevant to reducing by a Lie group along a submanifold. Our first example is Marsden–Weinstein–Meyer reduction, which we address in § 4.2. In § 4.3, we introduce the universal reduced spaces
$G$-spaces. In § 4.1, we derive some of the Lie-theoretic machinery relevant to reducing by a Lie group along a submanifold. Our first example is Marsden–Weinstein–Meyer reduction, which we address in § 4.2. In § 4.3, we introduce the universal reduced spaces ![]() $\mathfrak {M}_{G,S,\mathcal {H}}$ and
$\mathfrak {M}_{G,S,\mathcal {H}}$ and ![]() $\mathfrak {M}_{G,S}$ and prove Theorem D(i). We subsequently define and study the class of stable submanifolds
$\mathfrak {M}_{G,S}$ and prove Theorem D(i). We subsequently define and study the class of stable submanifolds ![]() $S\subseteq \mathfrak {g}^{*}$ in § 4.4; this is a particularly convenient class of submanifolds along which to reduce, and it includes all Poisson transversals and Poisson submanifolds. The proofs of parts (ii) and (iii) in Theorem D are also given in § 4.4. We then devote § 4.5 to the proof of Theorem D(iv). Theorem F is the subject of §§ 4.6–4.8, whereas Theorem E(ii) is proved in § 4.9.
$S\subseteq \mathfrak {g}^{*}$ in § 4.4; this is a particularly convenient class of submanifolds along which to reduce, and it includes all Poisson transversals and Poisson submanifolds. The proofs of parts (ii) and (iii) in Theorem D are also given in § 4.4. We then devote § 4.5 to the proof of Theorem D(iv). Theorem F is the subject of §§ 4.6–4.8, whereas Theorem E(ii) is proved in § 4.9.
Except for those instances in which we explicitly indicate otherwise, all material in this section can be interpreted in both the category of smooth manifolds and the category of complex manifolds. We simply use the terms manifolds and maps for smooth manifolds and smooth maps, or complex manifolds and holomorphic maps. A submanifold will refer to a smooth submanifold or a complex submanifold, and both are assumed to be embedded but not necessarily closed. A Lie group will mean a real Lie group or a complex Lie group, and we proceed analogously for Lie algebras. A symplectic form will mean a symplectic form on smooth manifold or a holomorphic symplectic form on a complex manifold, etc.
4.1 Main construction
The notion of a Hamiltonian system introduced in §§ 2 and 3 generalizes the standard one for Lie group actions [Reference Mikami and WeinsteinMW88, Examples 3.1 and 3.9]. Let us briefly recall the salient details.
Let ![]() $G$ be a Lie group with Lie algebra
$G$ be a Lie group with Lie algebra ![]() $\mathfrak {g}$, adjoint representation
$\mathfrak {g}$, adjoint representation ![]() $\mathrm {Ad} : G \longrightarrow \mathrm {GL}(\mathfrak {g})$, and coadjoint representation
$\mathrm {Ad} : G \longrightarrow \mathrm {GL}(\mathfrak {g})$, and coadjoint representation ![]() $\mathrm {Ad}^{*} : G \longrightarrow \mathrm {GL}(\mathfrak {g}^{*})$. We use the left trivialization
$\mathrm {Ad}^{*} : G \longrightarrow \mathrm {GL}(\mathfrak {g}^{*})$. We use the left trivialization
to freely identify ![]() $T^{*}G$ and
$T^{*}G$ and ![]() $G \times \mathfrak {g}^{*}$ throughout our paper. Let
$G \times \mathfrak {g}^{*}$ throughout our paper. Let ![]() $\Omega := d\Theta$ be the canonical symplectic form on
$\Omega := d\Theta$ be the canonical symplectic form on ![]() $T^{*}G$, where
$T^{*}G$, where ![]() $\Theta$ is the tautological
$\Theta$ is the tautological ![]() $1$-form. We have
$1$-form. We have
for all ![]() $(u_i, \zeta _i) \in \mathfrak {g} \times \mathfrak {g}^{*} = T_gG \times \mathfrak {g}^{*}=T_{(g, \xi )}(G \times \mathfrak {g}^{*})$ and
$(u_i, \zeta _i) \in \mathfrak {g} \times \mathfrak {g}^{*} = T_gG \times \mathfrak {g}^{*}=T_{(g, \xi )}(G \times \mathfrak {g}^{*})$ and ![]() $(g,\xi )\in G\times \mathfrak {g}^{*}=T^{*}G$, where
$(g,\xi )\in G\times \mathfrak {g}^{*}=T^{*}G$, where ![]() $T_gG$ is identified with
$T_gG$ is identified with ![]() $\mathfrak {g}$ by left translations (see e.g. [Reference Abraham and MarsdenAM78, Proposition 4.4.1]).
$\mathfrak {g}$ by left translations (see e.g. [Reference Abraham and MarsdenAM78, Proposition 4.4.1]).
Consider the ![]() $(G \times G)$-action on
$(G \times G)$-action on ![]() $G$ defined by
$G$ defined by
for all ![]() $(a, b) \in G \times G$ and
$(a, b) \in G \times G$ and ![]() $g \in G$. This action lifts to a Hamiltonian action on
$g \in G$. This action lifts to a Hamiltonian action on ![]() $T^{*}G = G \times \mathfrak {g}^{*}$ given by
$T^{*}G = G \times \mathfrak {g}^{*}$ given by
for all ![]() $(a, b) \in G \times G$ and
$(a, b) \in G \times G$ and ![]() $(g, \xi ) \in T^{*}G$, and it admits
$(g, \xi ) \in T^{*}G$, and it admits
as a moment map (see e.g. [Reference Abraham and MarsdenAM78, Theorem 4.4.3]).
The identification ![]() $T^{*}G = G \times \mathfrak {g}^{*}$ also shows that
$T^{*}G = G \times \mathfrak {g}^{*}$ also shows that ![]() $T^{*}G$ has the structure of a Lie groupoid, namely the action groupoid for the coadjoint representation. Explicitly,
$T^{*}G$ has the structure of a Lie groupoid, namely the action groupoid for the coadjoint representation. Explicitly, ![]() $T^{*}G \rightrightarrows \mathfrak {g}^{*}$ is a Lie groupoid with source and target maps
$T^{*}G \rightrightarrows \mathfrak {g}^{*}$ is a Lie groupoid with source and target maps
and multiplication
The canonical symplectic form on ![]() $T^{*}G$ then gives
$T^{*}G$ then gives ![]() $T^{*}G \rightrightarrows \mathfrak {g}^{*}$ the structure of a symplectic groupoid, called the cotangent groupoid of
$T^{*}G \rightrightarrows \mathfrak {g}^{*}$ the structure of a symplectic groupoid, called the cotangent groupoid of ![]() $G$. The Poisson bivector field
$G$. The Poisson bivector field ![]() $\sigma$ on the base
$\sigma$ on the base ![]() $\mathfrak {g}^{*}$ is the Kirillov–Kostant–Souriau structure given by
$\mathfrak {g}^{*}$ is the Kirillov–Kostant–Souriau structure given by
where ![]() $\mathrm {ad}_x : \mathfrak {g} \longrightarrow \mathfrak {g}$ is the adjoint action
$\mathrm {ad}_x : \mathfrak {g} \longrightarrow \mathfrak {g}$ is the adjoint action ![]() $\mathrm {ad}_x y = [x, y]$ of
$\mathrm {ad}_x y = [x, y]$ of ![]() $x\in \mathfrak {g}$ and
$x\in \mathfrak {g}$ and ![]() $\mathrm {ad}_x^{*} : \mathfrak {g}^{*} \longrightarrow \mathfrak {g}^{*}$ is its dual
$\mathrm {ad}_x^{*} : \mathfrak {g}^{*} \longrightarrow \mathfrak {g}^{*}$ is its dual ![]() $\mathrm {ad}_x^{*}\xi := -\xi \circ \mathrm {ad}_x$.
$\mathrm {ad}_x^{*}\xi := -\xi \circ \mathrm {ad}_x$.
A Hamiltonian ![]() $G$-space
$G$-space ![]() $(M, \omega )$ with moment
$(M, \omega )$ with moment ![]() $\mu : M \longrightarrow \mathfrak {g}^{*}$ is then equivalent to a Hamiltonian system (Definition 2.1) with underlying symplectic manifold
$\mu : M \longrightarrow \mathfrak {g}^{*}$ is then equivalent to a Hamiltonian system (Definition 2.1) with underlying symplectic manifold ![]() $(M, \omega )$, moment map
$(M, \omega )$, moment map ![]() $\mu$, and symplectic groupoid
$\mu$, and symplectic groupoid ![]() $T^{*}G \rightrightarrows \mathfrak {g}^{*}$; one simply lets
$T^{*}G \rightrightarrows \mathfrak {g}^{*}$; one simply lets ![]() $T^{*}G \rightrightarrows \mathfrak {g}^{*}$ act on
$T^{*}G \rightrightarrows \mathfrak {g}^{*}$ act on ![]() $M$ by
$M$ by
for all ![]() $(g, \xi ) \in T^{*}G$ and
$(g, \xi ) \in T^{*}G$ and ![]() $p \in M$ (see [Reference Mikami and WeinsteinMW88, Example 3.9]). In this context, we have the following counterpart of Definitions 2.15 and 3.11.
$p \in M$ (see [Reference Mikami and WeinsteinMW88, Example 3.9]). In this context, we have the following counterpart of Definitions 2.15 and 3.11.
Definition 4.1 Let ![]() $M$ be a Hamiltonian
$M$ be a Hamiltonian ![]() $G$-space with moment map
$G$-space with moment map ![]() $\mu : M \longrightarrow \mathfrak {g}^{*}$. A reduction datum for the action of
$\mu : M \longrightarrow \mathfrak {g}^{*}$. A reduction datum for the action of ![]() $G$ on
$G$ on ![]() $M$ is a reduction datum for the action of
$M$ is a reduction datum for the action of ![]() $T^{*}G \rightrightarrows \mathfrak {g}^{*}$ on
$T^{*}G \rightrightarrows \mathfrak {g}^{*}$ on ![]() $M$, i.e. a pair
$M$, i.e. a pair ![]() $(S, \mathcal {H})$ with
$(S, \mathcal {H})$ with ![]() $S \subseteq \mathfrak {g}^{*}$ a pre-Poisson submanifold and
$S \subseteq \mathfrak {g}^{*}$ a pre-Poisson submanifold and ![]() $\mathcal {H} \rightrightarrows S$ a stabilizer subgroupoid of
$\mathcal {H} \rightrightarrows S$ a stabilizer subgroupoid of ![]() $S$ in
$S$ in ![]() $T^{*}G \rightrightarrows \mathfrak {g}^{*}$. We say that
$T^{*}G \rightrightarrows \mathfrak {g}^{*}$. We say that ![]() $(S, \mathcal {H})$ is clean if it is a clean reduction datum for the action of
$(S, \mathcal {H})$ is clean if it is a clean reduction datum for the action of ![]() $T^{*}G \rightrightarrows \mathfrak {g}^{*}$ on
$T^{*}G \rightrightarrows \mathfrak {g}^{*}$ on ![]() $M$. In this case, the symplectic reduction of
$M$. In this case, the symplectic reduction of ![]() $M$ by
$M$ by ![]() $G$ along
$G$ along ![]() $S$ with respect to
$S$ with respect to ![]() $\mathcal {H}$ is defined to be
$\mathcal {H}$ is defined to be
If ![]() $\mathcal {H}$ is source-connected, we use the simplified notation
$\mathcal {H}$ is source-connected, we use the simplified notation
and call it the symplectic reduction of ![]() $M$ by
$M$ by ![]() $G$ along
$G$ along ![]() $S$.
$S$.
Remark 4.2 Although ![]() $G$ is a group,
$G$ is a group, ![]() $\mathcal {H}$ can be a non-trivial groupoid; see Theorem 5.10 and the discussion preceding it. One consequence is that
$\mathcal {H}$ can be a non-trivial groupoid; see Theorem 5.10 and the discussion preceding it. One consequence is that ![]() $M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S}} G$ might not be realizable as a quotient of
$M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S}} G$ might not be realizable as a quotient of ![]() $\mu ^{-1}(S)$ by a Lie group action.
$\mu ^{-1}(S)$ by a Lie group action.
Now recall that ![]() $T^{*}G\vert _S$ denotes the restriction of the cotangent groupoid to
$T^{*}G\vert _S$ denotes the restriction of the cotangent groupoid to ![]() $S\subseteq \mathfrak {g}^{*}$. This features in the following sufficient condition for
$S\subseteq \mathfrak {g}^{*}$. This features in the following sufficient condition for ![]() $M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S, \mathcal {H}}} G$ to be a symplectic manifold, which we state for future reference.
$M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S, \mathcal {H}}} G$ to be a symplectic manifold, which we state for future reference.
Lemma 4.3 Let ![]() $M$ be a Hamiltonian
$M$ be a Hamiltonian ![]() $G$-space with moment map
$G$-space with moment map ![]() $\mu : M \longrightarrow \mathfrak {g}^{*}$ and
$\mu : M \longrightarrow \mathfrak {g}^{*}$ and ![]() $(S, \mathcal {H})$ a reduction datum. If
$(S, \mathcal {H})$ a reduction datum. If ![]() $G$ acts freely and properly on
$G$ acts freely and properly on ![]() $M$ and
$M$ and ![]() $\mathcal {H}$ is closed in
$\mathcal {H}$ is closed in ![]() $T^{*}G\vert _S$, then
$T^{*}G\vert _S$, then ![]() $(S, \mathcal {H})$ is clean and
$(S, \mathcal {H})$ is clean and ![]() $M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S, \mathcal {H}}} G$ is a symplectic manifold.
$M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S, \mathcal {H}}} G$ is a symplectic manifold.
Proof. As the action of ![]() $G$ on
$G$ on ![]() $M$ is free, so is the action of
$M$ is free, so is the action of ![]() $\mathcal {H}$ on
$\mathcal {H}$ on ![]() $N := \mu ^{-1}(S)$. Theorem 2.20 or Proposition 3.14 then show that
$N := \mu ^{-1}(S)$. Theorem 2.20 or Proposition 3.14 then show that ![]() $S$ is transverse to
$S$ is transverse to ![]() $\mu$, and that it suffices to show the action of
$\mu$, and that it suffices to show the action of ![]() $\mathcal {H}$ on
$\mathcal {H}$ on ![]() $N$ to be proper. Note that the action of
$N$ to be proper. Note that the action of ![]() $T^{*}G \rightrightarrows \mathfrak {g}^{*}$ on
$T^{*}G \rightrightarrows \mathfrak {g}^{*}$ on ![]() $M$ is proper; (2.1) reduces to the map
$M$ is proper; (2.1) reduces to the map ![]() $G \times M \longrightarrow M \times M$,
$G \times M \longrightarrow M \times M$, ![]() $(g, p) \mapsto (p, g \cdot p)$, which is proper by assumption. The action of
$(g, p) \mapsto (p, g \cdot p)$, which is proper by assumption. The action of ![]() $\mathcal {H}$ on
$\mathcal {H}$ on ![]() $N$ is then proper by Proposition 2.21.
$N$ is then proper by Proposition 2.21.
We also record the following description of the stabilizer subalgebroid, which will be useful for examples.
Lemma 4.4 Let ![]() $S \subseteq \mathfrak {g}^{*}$ be a submanifold and let
$S \subseteq \mathfrak {g}^{*}$ be a submanifold and let ![]() $\sigma$ be the Kirillov–Kostant–Souriau Poisson structure on
$\sigma$ be the Kirillov–Kostant–Souriau Poisson structure on ![]() $\mathfrak {g}^{*}$. The subset
$\mathfrak {g}^{*}$. The subset ![]() $L_S := \sigma ^{-1}(TS) \cap TS^{\circ }$ of
$L_S := \sigma ^{-1}(TS) \cap TS^{\circ }$ of ![]() $\mathrm {Lie}(T^{*}G) = T^{*}\mathfrak {g}^{*} = \mathfrak {g} \times \mathfrak {g}^{*}$ is given by
$\mathrm {Lie}(T^{*}G) = T^{*}\mathfrak {g}^{*} = \mathfrak {g} \times \mathfrak {g}^{*}$ is given by
Proof. This follows from the expression for ![]() $\sigma$ given by (4.4).
$\sigma$ given by (4.4).
The following observation will be useful for showing that certain subgroupoids are in fact stabilizer subgroupoids.
Lemma 4.5 Let ![]() $\mathcal {H} \rightrightarrows S$ be an embedded Lie subgroupoid of
$\mathcal {H} \rightrightarrows S$ be an embedded Lie subgroupoid of ![]() $T^{*}G \rightrightarrows \mathfrak {g}^{*}$ over any submanifold
$T^{*}G \rightrightarrows \mathfrak {g}^{*}$ over any submanifold ![]() $S \subseteq \mathfrak {g}^{*}$.
$S \subseteq \mathfrak {g}^{*}$.
(i) We have
for some collection of submanifolds \begin{align*} \mathcal{H} = \{(g, \xi) \in G \times S : g \in \mathcal{H}_\xi\} \end{align*}
\begin{align*} \mathcal{H} = \{(g, \xi) \in G \times S : g \in \mathcal{H}_\xi\} \end{align*} $\mathcal {H}_\xi \subseteq G$,
$\mathcal {H}_\xi \subseteq G$,  $\xi \in S$, each containing the identity
$\xi \in S$, each containing the identity  $1 \in G$.
$1 \in G$.(ii) The Lie algebroid of
 $\mathcal {H}$ is the Lie subalgebroid of
$\mathcal {H}$ is the Lie subalgebroid of  $\mathrm {Lie}(T^{*}G) = \mathfrak {g} \times \mathfrak {g}^{*}$ given by
$\mathrm {Lie}(T^{*}G) = \mathfrak {g} \times \mathfrak {g}^{*}$ given by
 \begin{align*} \mathrm{Lie}(\mathcal{H}) = \{(x, \xi) \in \mathfrak{g} \times S : x \in T_1\mathcal{H}_\xi\}. \end{align*}
\begin{align*} \mathrm{Lie}(\mathcal{H}) = \{(x, \xi) \in \mathfrak{g} \times S : x \in T_1\mathcal{H}_\xi\}. \end{align*}
Proof. Let ![]() $\mathsf {s}, \mathsf {t} : T^{*}G \rightrightarrows \mathfrak {g}^{*}$ be the source and target maps (4.3). As
$\mathsf {s}, \mathsf {t} : T^{*}G \rightrightarrows \mathfrak {g}^{*}$ be the source and target maps (4.3). As ![]() $\xi = \mathsf {t}(g, \xi ) \in S$ for all
$\xi = \mathsf {t}(g, \xi ) \in S$ for all ![]() $(g, \xi ) \in \mathcal {H}$, we have
$(g, \xi ) \in \mathcal {H}$, we have
with ![]() $\mathcal {H}_\xi := \{g \in G : (g, \xi ) \in \mathcal {H}\}$. Note that
$\mathcal {H}_\xi := \{g \in G : (g, \xi ) \in \mathcal {H}\}$. Note that ![]() $\mathcal {H}_\xi \times \{\xi \}$ is the target fiber of
$\mathcal {H}_\xi \times \{\xi \}$ is the target fiber of ![]() $\mathcal {H}$ over
$\mathcal {H}$ over ![]() $\xi$, so that
$\xi$, so that ![]() $\mathcal {H}_\xi$ is necessarily smooth. This completes the proof of part (i).
$\mathcal {H}_\xi$ is necessarily smooth. This completes the proof of part (i).
To verify part (ii), note that the restriction ![]() $(\ker d\mathsf {t})\vert _{\{1\} \times \mathfrak {g}^{*}}$ of
$(\ker d\mathsf {t})\vert _{\{1\} \times \mathfrak {g}^{*}}$ of ![]() $\ker d\mathsf {t}$ to the identity section
$\ker d\mathsf {t}$ to the identity section ![]() $\{1\} \times \mathfrak {g}^{*} \subseteq G\times \mathfrak {g}^{*} = T^{*}G$ is the trivial vector bundle
$\{1\} \times \mathfrak {g}^{*} \subseteq G\times \mathfrak {g}^{*} = T^{*}G$ is the trivial vector bundle ![]() $\mathfrak {g} \times \mathfrak {g}^{*}$ over
$\mathfrak {g} \times \mathfrak {g}^{*}$ over ![]() $\mathfrak {g}^{*}$. From (4.1), we see that the canonical isomorphism
$\mathfrak {g}^{*}$. From (4.1), we see that the canonical isomorphism ![]() $(\ker d\mathsf {t})\vert _{\{1\} \times \mathfrak {g}^{*}} \longrightarrow T^{*}\mathfrak {g}^{*} = \mathfrak {g} \times \mathfrak {g}^{*}$ given by (2.2) is
$(\ker d\mathsf {t})\vert _{\{1\} \times \mathfrak {g}^{*}} \longrightarrow T^{*}\mathfrak {g}^{*} = \mathfrak {g} \times \mathfrak {g}^{*}$ given by (2.2) is
It follows that the Lie subalgebroid of ![]() $T^{*}\mathfrak {g}^{*}$ induced by
$T^{*}\mathfrak {g}^{*}$ induced by ![]() $\mathcal {H}$ is as claimed.
$\mathcal {H}$ is as claimed.
4.2 Marsden–Weinstein–Meyer reduction
We now show that Marsden–Weinstein–Meyer reduction can be recovered as symplectic reduction along a singleton.
Let ![]() $G$ be a Lie group acting on a symplectic manifold
$G$ be a Lie group acting on a symplectic manifold ![]() $(M, \omega )$ in a Hamiltonian way with moment map
$(M, \omega )$ in a Hamiltonian way with moment map ![]() $\mu : M \longrightarrow \mathfrak {g}^{*}$. Let
$\mu : M \longrightarrow \mathfrak {g}^{*}$. Let ![]() $H \subseteq G$ be an immersed Lie subgroup with Lie algebra
$H \subseteq G$ be an immersed Lie subgroup with Lie algebra ![]() $\mathfrak {h} \subseteq \mathfrak {g}$ and let
$\mathfrak {h} \subseteq \mathfrak {g}$ and let ![]() $\xi \in \mathfrak {g}^{*}$. Let
$\xi \in \mathfrak {g}^{*}$. Let ![]() $H_\xi$ be the stabilizer subgroup of
$H_\xi$ be the stabilizer subgroup of ![]() $\xi \vert _\mathfrak {h} \in \mathfrak {h}^{*}$ in
$\xi \vert _\mathfrak {h} \in \mathfrak {h}^{*}$ in ![]() $H$, and consider the annihilator
$H$, and consider the annihilator ![]() $\mathfrak {h}^{\circ }\subseteq \mathfrak {g}^{*}$ of
$\mathfrak {h}^{\circ }\subseteq \mathfrak {g}^{*}$ of ![]() $\mathfrak {h}$.
$\mathfrak {h}$.
Lemma 4.6 (Cf. [Reference Cattaneo and ZambonCZ07, Proposition 5.1 and Example 6.2])
The affine linear subspace ![]() $\xi + \mathfrak {h}^{\circ } \subseteq \mathfrak {g}^{*}$ is pre-Poisson and
$\xi + \mathfrak {h}^{\circ } \subseteq \mathfrak {g}^{*}$ is pre-Poisson and
is a stabilizer subgroupoid of ![]() $\xi + \mathfrak {h}^{\circ }$ in
$\xi + \mathfrak {h}^{\circ }$ in ![]() $T^{*}G \rightrightarrows \mathfrak {g}^{*}$.
$T^{*}G \rightrightarrows \mathfrak {g}^{*}$.
Proof. Lemma 4.4 implies that
where ![]() $\mathfrak {h}_\xi := \operatorname {Lie}(H_\xi )$. By Lemma 4.5(ii), the Lie algebroid of
$\mathfrak {h}_\xi := \operatorname {Lie}(H_\xi )$. By Lemma 4.5(ii), the Lie algebroid of ![]() $\mathcal {H}$ is
$\mathcal {H}$ is ![]() $L_{\xi + \mathfrak {h}^{\circ }}$. It then only remains to show that
$L_{\xi + \mathfrak {h}^{\circ }}$. It then only remains to show that ![]() $\mathcal {H}$ is isotropic in
$\mathcal {H}$ is isotropic in ![]() $T^{*}G$. To this end, let
$T^{*}G$. To this end, let ![]() $(h, \xi + \eta ) \in \mathcal {H}$, and let
$(h, \xi + \eta ) \in \mathcal {H}$, and let ![]() $(u_i, \zeta _i) \in T_{(h, \xi + \eta )}\mathcal {H} = \mathfrak {h}_\xi \times \mathfrak {h}^{\circ }$,
$(u_i, \zeta _i) \in T_{(h, \xi + \eta )}\mathcal {H} = \mathfrak {h}_\xi \times \mathfrak {h}^{\circ }$, ![]() $i \in \{1, 2\}$. Equation (4.1) implies that
$i \in \{1, 2\}$. Equation (4.1) implies that
and we see that each term vanishes.
In light of this result, we may consider the symplectic reduction
By viewing ![]() $\xi$ as an element of
$\xi$ as an element of ![]() $\mathfrak {g}^{*} / \mathfrak {h}^{\circ } = \mathfrak {h}^{*}$, we also have the symplectic reduction of
$\mathfrak {g}^{*} / \mathfrak {h}^{\circ } = \mathfrak {h}^{*}$, we also have the symplectic reduction of ![]() $M$ by
$M$ by ![]() $H$ at level
$H$ at level ![]() $\xi$:
$\xi$:
where ![]() $\mu _\mathfrak {h} : M \longrightarrow \mathfrak {h}^{*}$ is the induced moment map for the action of
$\mu _\mathfrak {h} : M \longrightarrow \mathfrak {h}^{*}$ is the induced moment map for the action of ![]() $H$ on
$H$ on ![]() $M$. We have
$M$. We have ![]() $\mu _\mathfrak {h}^{-1}(\xi ) = \mu ^{-1}(\xi + \mathfrak {h}^{\circ })$, so these two symplectic reductions coincide.
$\mu _\mathfrak {h}^{-1}(\xi ) = \mu ^{-1}(\xi + \mathfrak {h}^{\circ })$, so these two symplectic reductions coincide.
Proposition 4.7 We have ![]() $M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{\xi + \mathfrak {h}^{\circ }, \mathcal {H}}} G = M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{\xi }} H$, where
$M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{\xi + \mathfrak {h}^{\circ }, \mathcal {H}}} G = M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{\xi }} H$, where ![]() $\mathcal {H}$ is given by (4.5).
$\mathcal {H}$ is given by (4.5).
Taking ![]() $\mathfrak {h}=\mathfrak {g}$ then yields the following corollary.
$\mathfrak {h}=\mathfrak {g}$ then yields the following corollary.
Corollary 4.8 Let ![]() $\xi \in \mathfrak {g}^{*}$. Then
$\xi \in \mathfrak {g}^{*}$. Then ![]() $\mathcal {H} := G_\xi \times \{\xi \}$ is a stabilizer subgroupoid of
$\mathcal {H} := G_\xi \times \{\xi \}$ is a stabilizer subgroupoid of ![]() $\{\xi \}$ in
$\{\xi \}$ in ![]() $T^{*}G \rightrightarrows \mathfrak {g}^{*}$ and
$T^{*}G \rightrightarrows \mathfrak {g}^{*}$ and
is the Marsden–Weinstein–Meyer reduced space at level ![]() $\xi$.
$\xi$.
Remark 4.9 Let ![]() $\mathcal {G} \rightrightarrows X$ be a symplectic groupoid and
$\mathcal {G} \rightrightarrows X$ be a symplectic groupoid and ![]() $S \subseteq X$ a pre-Poisson submanifold. One consequence of this subsection is that there may not exist any stabilizer subgroupoid
$S \subseteq X$ a pre-Poisson submanifold. One consequence of this subsection is that there may not exist any stabilizer subgroupoid ![]() $\mathcal {H} \rightrightarrows S$ of
$\mathcal {H} \rightrightarrows S$ of ![]() $S$ that is closed in
$S$ that is closed in ![]() $\mathcal {G}\vert _S$. To see this, let
$\mathcal {G}\vert _S$. To see this, let ![]() $\mathfrak {h}\subseteq \mathfrak {g}$ be a Lie subalgebra. Any stabilizer subgroupoid of
$\mathfrak {h}\subseteq \mathfrak {g}$ be a Lie subalgebra. Any stabilizer subgroupoid of ![]() $\mathfrak {h}^{\circ }\subseteq \mathfrak {g}^{*}$ in the cotangent groupoid
$\mathfrak {h}^{\circ }\subseteq \mathfrak {g}^{*}$ in the cotangent groupoid ![]() $T^{*}G\rightrightarrows \mathfrak {g}^{*}$ must take the form
$T^{*}G\rightrightarrows \mathfrak {g}^{*}$ must take the form ![]() $H\times \mathfrak {h}^{\circ }$, where
$H\times \mathfrak {h}^{\circ }$, where ![]() $H$ is a Lie subgroup of
$H$ is a Lie subgroup of ![]() $G$ with Lie algebra
$G$ with Lie algebra ![]() $\mathfrak {h}$. It now just remains to observe that
$\mathfrak {h}$. It now just remains to observe that ![]() $\mathcal {H}$ is closed in
$\mathcal {H}$ is closed in ![]() $\mathcal {G}$ if and only if
$\mathcal {G}$ if and only if ![]() $H$ is closed in
$H$ is closed in ![]() $G$.
$G$.
4.3 The universal reduced spaces
Let ![]() $G$ be a Lie group and recall the Hamiltonian
$G$ be a Lie group and recall the Hamiltonian ![]() $(G\times G)$-action on
$(G\times G)$-action on ![]() $T^{*}G$ and moment map
$T^{*}G$ and moment map ![]() $\mu :T^{*}G \longrightarrow \mathfrak {g}^{*} \times \mathfrak {g}^{*}$ discussed in § 4.1. We refer to the Hamiltonian action of
$\mu :T^{*}G \longrightarrow \mathfrak {g}^{*} \times \mathfrak {g}^{*}$ discussed in § 4.1. We refer to the Hamiltonian action of ![]() $G \cong G \times \{1\} \subseteq G \times G$ on
$G \cong G \times \{1\} \subseteq G \times G$ on ![]() $T^{*}G$ as the action by left translations. Similarly, the action of
$T^{*}G$ as the action by left translations. Similarly, the action of ![]() $G \cong \{1\} \times G$ on
$G \cong \{1\} \times G$ on ![]() $T^{*}G$ is called the action by right translations.
$T^{*}G$ is called the action by right translations.
Let us suppose that ![]() $S \subseteq \mathfrak {g}^{*}$ is a pre-Poisson submanifold, that
$S \subseteq \mathfrak {g}^{*}$ is a pre-Poisson submanifold, that ![]() $\mathcal {H} \rightrightarrows S$ is a stabilizer subgroupoid of
$\mathcal {H} \rightrightarrows S$ is a stabilizer subgroupoid of ![]() $S$ in
$S$ in ![]() $T^{*}G \rightrightarrows \mathfrak {g}^{*}$, and that
$T^{*}G \rightrightarrows \mathfrak {g}^{*}$, and that ![]() $(S, \mathcal {H})$ is a clean reduction datum with respect to the action of
$(S, \mathcal {H})$ is a clean reduction datum with respect to the action of ![]() $G$ on
$G$ on ![]() $T^{*}G$ by right translations. It follows that
$T^{*}G$ by right translations. It follows that
is a symplectic manifold, which we call the universal reduced space associated to ![]() $(G, S, \mathcal {H})$; Theorem 4.11 will elucidate this choice of nomenclature. Remark 3.12 justifies using the simplified notation
$(G, S, \mathcal {H})$; Theorem 4.11 will elucidate this choice of nomenclature. Remark 3.12 justifies using the simplified notation
where ![]() $\mathcal {H}\rightrightarrows S$ is any source-connected stabilizer subgroupoid of
$\mathcal {H}\rightrightarrows S$ is any source-connected stabilizer subgroupoid of ![]() $S$ in
$S$ in ![]() $T^{*}G$. As the action of
$T^{*}G$. As the action of ![]() $G$ on
$G$ on ![]() $T^{*}G$ is proper, we observe that
$T^{*}G$ is proper, we observe that ![]() $(S, \mathcal {H})$ is clean if
$(S, \mathcal {H})$ is clean if ![]() $\mathcal {H}$ is closed in
$\mathcal {H}$ is closed in ![]() $T^{*}G\vert _S$ (Lemma 4.3). We also observe that the action of
$T^{*}G\vert _S$ (Lemma 4.3). We also observe that the action of ![]() $G$ on
$G$ on ![]() $T^{*}G$ by left translations descends to a Hamiltonian
$T^{*}G$ by left translations descends to a Hamiltonian ![]() $G$-action on
$G$-action on ![]() $\mathfrak {M}_{G, S,\mathcal {H}} = (G \times S) / \mathcal {H}$ given by
$\mathfrak {M}_{G, S,\mathcal {H}} = (G \times S) / \mathcal {H}$ given by
for all ![]() $a, g \in G$ and
$a, g \in G$ and ![]() $\xi \in S$. The corresponding moment map is induced by the first component of
$\xi \in S$. The corresponding moment map is induced by the first component of ![]() $\mu :T^{*}G\longrightarrow \mathfrak {g}^{*}\oplus \mathfrak {g}^{*}$, i.e. it is given by
$\mu :T^{*}G\longrightarrow \mathfrak {g}^{*}\oplus \mathfrak {g}^{*}$, i.e. it is given by
We may summarize the previous discussion as follows.
Proposition 4.10 Let ![]() $S \subseteq \mathfrak {g}^{*}$ be a pre-Poisson submanifold and
$S \subseteq \mathfrak {g}^{*}$ be a pre-Poisson submanifold and ![]() $\mathcal {H} \rightrightarrows S$ a stabilizer subgroupoid of
$\mathcal {H} \rightrightarrows S$ a stabilizer subgroupoid of ![]() $S$ in
$S$ in ![]() $T^{*}G \rightrightarrows \mathfrak {g}^{*}$.
$T^{*}G \rightrightarrows \mathfrak {g}^{*}$.
(i) Suppose that
 $(S, \mathcal {H})$ is a clean reduction datum for the action of
$(S, \mathcal {H})$ is a clean reduction datum for the action of  $G$ on
$G$ on  $T^{*}G$ by right translations. The universal reduced space
$T^{*}G$ by right translations. The universal reduced space  $\mathfrak {M}_{G, S, \mathcal {H}}$ is then a Hamiltonian
$\mathfrak {M}_{G, S, \mathcal {H}}$ is then a Hamiltonian  $G$-space with action (4.6) and moment map (4.7). It has dimension
$G$-space with action (4.6) and moment map (4.7). It has dimension
 \begin{align*} \dim \mathfrak{M}_{G, S, \mathcal{H}} = \dim \mathfrak{g} + \dim S - \operatorname{rk} L_S. \end{align*}
\begin{align*} \dim \mathfrak{M}_{G, S, \mathcal{H}} = \dim \mathfrak{g} + \dim S - \operatorname{rk} L_S. \end{align*}(ii) The hypothesis of part (i) is satisfied if
 $\mathcal {H}$ is closed in
$\mathcal {H}$ is closed in  $T^{*}G\vert _S$.
$T^{*}G\vert _S$.
Proof. It only remains to prove the formula for the dimension; this is simply a result of ![]() $\mathcal {H}$ acting freely on
$\mathcal {H}$ acting freely on ![]() $G\times S$ and the fact that
$G\times S$ and the fact that ![]() $\mathfrak {M}_{G, S, \mathcal {H}} = (G \times S) / \mathcal {H}$.
$\mathfrak {M}_{G, S, \mathcal {H}} = (G \times S) / \mathcal {H}$.
The following result is analogous to the universal property of symplectic implosion [Reference Guillemin, Jeffrey and SjamaarGJS02, § 4].
Theorem 4.11 (Universality; Theorem D(i))
Let ![]() $G$ be a Lie group acting on a symplectic manifold
$G$ be a Lie group acting on a symplectic manifold ![]() $M$ in a Hamiltonian way with moment map
$M$ in a Hamiltonian way with moment map ![]() $\mu : M \longrightarrow \mathfrak {g}^{*}$. Let
$\mu : M \longrightarrow \mathfrak {g}^{*}$. Let ![]() $(S, \mathcal {H})$ be a clean reduction datum for both the action of
$(S, \mathcal {H})$ be a clean reduction datum for both the action of ![]() $G$ on
$G$ on ![]() $M$ and the action of
$M$ and the action of ![]() $G$ on
$G$ on ![]() $T^{*}G$ by right translations. We then have a canonical symplectomorphism
$T^{*}G$ by right translations. We then have a canonical symplectomorphism
where ![]() $G$ acts on
$G$ acts on ![]() $M \times \mathfrak {M}_{G, S, \mathcal {H}}^{-}$ diagonally and
$M \times \mathfrak {M}_{G, S, \mathcal {H}}^{-}$ diagonally and ![]() $\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{0}}$ denotes Marsden–Weinstein–Meyer reduction at level
$\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{0}}$ denotes Marsden–Weinstein–Meyer reduction at level ![]() $0$.
$0$.
Proof. The map
descends to a diffeomorphism
where ![]() $\nu$ is the moment map (4.7). It then remains to show that
$\nu$ is the moment map (4.7). It then remains to show that ![]() $\psi ^{*}(\omega, -\Omega ) = i^{*}\omega$, where
$\psi ^{*}(\omega, -\Omega ) = i^{*}\omega$, where ![]() $i : \mu ^{-1}(S) \longrightarrow M$ is the inclusion map. However,
$i : \mu ^{-1}(S) \longrightarrow M$ is the inclusion map. However, ![]() $d\psi (u) = (u, 0, d\mu (u))$ for
$d\psi (u) = (u, 0, d\mu (u))$ for ![]() $u \in T\mu ^{-1}(S)$, so
$u \in T\mu ^{-1}(S)$, so
for all ![]() $p \in \mu ^{-1}(S)$ and
$p \in \mu ^{-1}(S)$ and ![]() $u, v \in T_p\mu ^{-1}(S)$.
$u, v \in T_p\mu ^{-1}(S)$.
Remark 4.12 (Kähler quotients)
The following remark only applies in the smooth category. Let ![]() $G$ be a compact Lie group and
$G$ be a compact Lie group and ![]() $(M, \omega )$ a Hamiltonian
$(M, \omega )$ a Hamiltonian ![]() $G$-space with moment map
$G$-space with moment map ![]() $\mu : M \longrightarrow \mathfrak {g}^{*}$. Suppose that
$\mu : M \longrightarrow \mathfrak {g}^{*}$. Suppose that ![]() $M$ has a
$M$ has a ![]() $G$-invariant Kähler metric compatible with
$G$-invariant Kähler metric compatible with ![]() $\omega$. The symplectic reduction
$\omega$. The symplectic reduction ![]() $M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{\xi }} G := \mu ^{-1}(\xi ) / G_\xi$ at level
$M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{\xi }} G := \mu ^{-1}(\xi ) / G_\xi$ at level ![]() $\xi \in \mathfrak {g}^{*}$ is then also Kähler if it is smooth [Reference Hitchin, Karlhede, Lindström and RočekHKLR87, § 3(C)]. It is natural to ask whether the same holds for a general symplectic reduction
$\xi \in \mathfrak {g}^{*}$ is then also Kähler if it is smooth [Reference Hitchin, Karlhede, Lindström and RočekHKLR87, § 3(C)]. It is natural to ask whether the same holds for a general symplectic reduction ![]() $M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S}} G$ along a pre-Poisson submanifold
$M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S}} G$ along a pre-Poisson submanifold ![]() $S \subseteq \mathfrak {g}^{*}$. An immediate corollary of universality (Theorem 4.11) is that it suffices to ask this question for the universal reduced space; if
$S \subseteq \mathfrak {g}^{*}$. An immediate corollary of universality (Theorem 4.11) is that it suffices to ask this question for the universal reduced space; if ![]() $\mathfrak {M}_{G, S, \mathcal {H}}$ has a compatible
$\mathfrak {M}_{G, S, \mathcal {H}}$ has a compatible ![]() $G$-invariant Kähler structure, then
$G$-invariant Kähler structure, then ![]() $M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S, \mathcal {H}}} G$ is also Kähler.
$M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S, \mathcal {H}}} G$ is also Kähler.
One might then expect the Kähler structure on ![]() $T^{*}G \cong G_\mathbb {C}$ to induce a Kähler structure on
$T^{*}G \cong G_\mathbb {C}$ to induce a Kähler structure on ![]() $\mathfrak {M}_{G, S, \mathcal {H}}$. However, the standard methods for showing that
$\mathfrak {M}_{G, S, \mathcal {H}}$. However, the standard methods for showing that ![]() $M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{\xi }} G$ is Kähler (e.g. [Reference Hitchin, Karlhede, Lindström and RočekHKLR87, § 3(C)] or [Reference KirwanKir84]) do not generalize to the case of symplectic reduction along a submanifold. For instance, suppose that
$M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{\xi }} G$ is Kähler (e.g. [Reference Hitchin, Karlhede, Lindström and RočekHKLR87, § 3(C)] or [Reference KirwanKir84]) do not generalize to the case of symplectic reduction along a submanifold. For instance, suppose that ![]() $S$ is a Poisson transversal in
$S$ is a Poisson transversal in ![]() $\mathfrak {g}^{*}$. We then have
$\mathfrak {g}^{*}$. We then have ![]() $\mathfrak {M}_{G, S} = G \times S$ (Example 2.27), which is a complex submanifold of
$\mathfrak {M}_{G, S} = G \times S$ (Example 2.27), which is a complex submanifold of ![]() $G_\mathbb {C}$ if and only if
$G_\mathbb {C}$ if and only if ![]() $S$ is open in
$S$ is open in ![]() $\mathfrak {g}^{*}$. On the other hand, there are special cases in which it is possible to define a Kähler structure on
$\mathfrak {g}^{*}$. On the other hand, there are special cases in which it is possible to define a Kähler structure on ![]() $\mathfrak {M}_{G, S, \mathcal {H}}$ indirectly; symplectic implosion [Reference Guillemin, Jeffrey and SjamaarGJS02, § 6] is a noteworthy example (see § 4.7).
$\mathfrak {M}_{G, S, \mathcal {H}}$ indirectly; symplectic implosion [Reference Guillemin, Jeffrey and SjamaarGJS02, § 6] is a noteworthy example (see § 4.7).
4.4 Symplectic reduction along stable submanifolds
We now study a large class of pre-Poisson submanifolds that encompasses most of the examples in this paper. The principal advantage of working with these submanifolds is that their stabilizer subgroupoids can be readily computed as Lie group fibrations (also known as group schemes).
Definition 4.13 Let ![]() $(X, \sigma )$ be a Poisson manifold. A submanifold
$(X, \sigma )$ be a Poisson manifold. A submanifold ![]() $S \subseteq X$ is called stable if it is pre-Poisson and its stabilizer subalgebroid
$S \subseteq X$ is called stable if it is pre-Poisson and its stabilizer subalgebroid ![]() $L_S$ is contained in
$L_S$ is contained in ![]() $\ker \sigma$.
$\ker \sigma$.
Lemma 4.14 Poisson submanifolds are stable.
Proof. A submanifold ![]() $S \subseteq X$ is Poisson if and only if
$S \subseteq X$ is Poisson if and only if ![]() $\sigma (TS^{\circ }) = 0$. In this case,
$\sigma (TS^{\circ }) = 0$. In this case,
so ![]() $L_S$ has constant rank. The condition
$L_S$ has constant rank. The condition ![]() $\sigma (TS^{\circ }) = 0$ also implies that
$\sigma (TS^{\circ }) = 0$ also implies that ![]() $L_S \subseteq \ker \sigma$.
$L_S \subseteq \ker \sigma$.
Lemma 4.15 Poisson transversals are stable.
Proof. By Example 2.27, a Poisson transversal ![]() $S$ satisfies
$S$ satisfies ![]() $L_S = 0$.
$L_S = 0$.
Let ![]() $G$ be a Lie group with Lie algebra
$G$ be a Lie group with Lie algebra ![]() $\mathfrak {g}$. We specialize to the case of
$\mathfrak {g}$. We specialize to the case of ![]() $X = \mathfrak {g}^{*}$ with its Kirillov–Kostant–Souriau Poisson structure
$X = \mathfrak {g}^{*}$ with its Kirillov–Kostant–Souriau Poisson structure ![]() $\sigma$ in (4.4). A pre-Poisson submanifold
$\sigma$ in (4.4). A pre-Poisson submanifold ![]() $S \subseteq \mathfrak {g}^{*}$ is then stable if and only if
$S \subseteq \mathfrak {g}^{*}$ is then stable if and only if ![]() $(L_S)_\xi \subseteq \mathfrak {g}_\xi$ for all
$(L_S)_\xi \subseteq \mathfrak {g}_\xi$ for all ![]() $\xi \in S$, where
$\xi \in S$, where ![]() $(L_S)_\xi$ is given by Lemma 4.4 and
$(L_S)_\xi$ is given by Lemma 4.4 and
Lemma 4.16 A ![]() $G$-invariant submanifold
$G$-invariant submanifold ![]() $S \subseteq \mathfrak {g}^{*}$ is Poisson and, hence, stable.
$S \subseteq \mathfrak {g}^{*}$ is Poisson and, hence, stable.
Proof. For all ![]() $\xi \in S$ and
$\xi \in S$ and ![]() $x \in T^{*}_\xi \mathfrak {g}^{*} = \mathfrak {g}$, we have
$x \in T^{*}_\xi \mathfrak {g}^{*} = \mathfrak {g}$, we have ![]() $\sigma _\xi (x) = -\mathrm {ad}_x^{*}\xi \in T_\xi S$.
$\sigma _\xi (x) = -\mathrm {ad}_x^{*}\xi \in T_\xi S$.
We now show that the stabilizer subgroupoids of stable submanifolds take a particularly simple form.
Theorem 4.17 (Theorem D(ii) and (iii))
Let ![]() $S \subseteq \mathfrak {g}^{*}$ be a stable submanifold. For each
$S \subseteq \mathfrak {g}^{*}$ be a stable submanifold. For each ![]() $\xi \in S$, let
$\xi \in S$, let ![]() $H_\xi \subseteq G$ be a Lie subgroup with Lie algebra
$H_\xi \subseteq G$ be a Lie subgroup with Lie algebra ![]() $\mathfrak {h}_\xi$. Consider the set
$\mathfrak {h}_\xi$. Consider the set
(i) The subspace
(4.8)is a Lie subalgebra of \begin{equation} \mathfrak{h}_\xi := (T_\xi S)^{\circ} \cap \mathfrak{g}_\xi \end{equation}
\begin{equation} \mathfrak{h}_\xi := (T_\xi S)^{\circ} \cap \mathfrak{g}_\xi \end{equation} $\mathfrak {g}$ for all
$\mathfrak {g}$ for all  $\xi \in S$, and the stabilizer subalgebroid of
$\xi \in S$, and the stabilizer subalgebroid of  $S$ is
$S$ is
 \begin{align*} L_S = \{(x, \xi) \in \mathfrak{g} \times S : x \in \mathfrak{h}_\xi\}. \end{align*}
\begin{align*} L_S = \{(x, \xi) \in \mathfrak{g} \times S : x \in \mathfrak{h}_\xi\}. \end{align*}(ii) Suppose that the following two conditions hold:
(C1)
 $\mathcal {H}$ is a submanifold of
$\mathcal {H}$ is a submanifold of  $T^{*}G$;
$T^{*}G$;(C2)
 $\mathcal {H}$ is isotropic in
$\mathcal {H}$ is isotropic in  $T^{*}G$.
$T^{*}G$.
 $\mathcal {H}$ is a stabilizer subgroupoid of
$\mathcal {H}$ is a stabilizer subgroupoid of  $S$ in
$S$ in  $T^{*}G \rightrightarrows \mathfrak {g}^{*}$.
$T^{*}G \rightrightarrows \mathfrak {g}^{*}$.(iii) If (C1) holds and there is an open dense subset
 $U$ of
$U$ of  $S$ such that
$S$ such that  $H_\xi$ is connected for all
$H_\xi$ is connected for all  $\xi \in U$, then (C2) also holds.
$\xi \in U$, then (C2) also holds.(iv) If
 $\mathcal {H}$ is closed in
$\mathcal {H}$ is closed in  $G \times S$ and each
$G \times S$ and each  $H_\xi$ is connected, then both (C1) and (C2) hold.
$H_\xi$ is connected, then both (C1) and (C2) hold.
Proof. As ![]() $L_S \subseteq \ker \sigma$, the anchor map of
$L_S \subseteq \ker \sigma$, the anchor map of ![]() $L_S$ is trivial. It follows that
$L_S$ is trivial. It follows that ![]() $L_S$ is a bundle of Lie subalgebras. We have
$L_S$ is a bundle of Lie subalgebras. We have
because ![]() $(L_S)_\xi \subseteq \ker \sigma _\xi$. This verifies part (i). Parts (ii) and (iii) follow from Lemma 4.5(ii) and Remark 2.9(ii). Part (iv) results from the following generalization of the closed subgroup theorem.
$(L_S)_\xi \subseteq \ker \sigma _\xi$. This verifies part (i). Parts (ii) and (iii) follow from Lemma 4.5(ii) and Remark 2.9(ii). Part (iv) results from the following generalization of the closed subgroup theorem.
Theorem 4.18 Let ![]() $G$ be a Lie group with Lie algebra
$G$ be a Lie group with Lie algebra ![]() $\mathfrak {g}$ and let
$\mathfrak {g}$ and let ![]() $S$ be a manifold. Suppose that
$S$ be a manifold. Suppose that ![]() $E$ is a subbundle of the trivial vector bundle
$E$ is a subbundle of the trivial vector bundle ![]() $\mathfrak {g} \times S \longrightarrow S$ such that the fiber
$\mathfrak {g} \times S \longrightarrow S$ such that the fiber ![]() $E_{\xi }$ over each
$E_{\xi }$ over each ![]() $\xi \in S$ is a Lie subalgebra of
$\xi \in S$ is a Lie subalgebra of ![]() $\mathfrak {g}$. Let
$\mathfrak {g}$. Let ![]() $H_\xi$ be the connected Lie subgroup of
$H_\xi$ be the connected Lie subgroup of ![]() $G$ with Lie algebra
$G$ with Lie algebra ![]() $E_\xi$ for each
$E_\xi$ for each ![]() $\xi \in S$, and set
$\xi \in S$, and set
If ![]() $\mathcal {H}$ is a closed subset of
$\mathcal {H}$ is a closed subset of ![]() $G \times S$, then it is a submanifold of
$G \times S$, then it is a submanifold of ![]() $G \times S$.
$G \times S$.
Proof. As this is a local statement, we may assume that there is a complement ![]() $F \subseteq \mathfrak {g} \times S$ to
$F \subseteq \mathfrak {g} \times S$ to ![]() $E$, so that
$E$, so that ![]() $\mathfrak {g} \times S = E \oplus F$. Consider the exponential map
$\mathfrak {g} \times S = E \oplus F$. Consider the exponential map ![]() $\mathfrak {g}\longrightarrow G$,
$\mathfrak {g}\longrightarrow G$, ![]() $x\longmapsto e^{x}$, and define
$x\longmapsto e^{x}$, and define
Let us also fix ![]() $\xi _0 \in S$. We claim that there exists a neighborhood
$\xi _0 \in S$. We claim that there exists a neighborhood ![]() $U$ of
$U$ of ![]() $(0, \xi _0)$ in
$(0, \xi _0)$ in ![]() $\mathfrak {g} \times S$ such that
$\mathfrak {g} \times S$ such that ![]() $\Phi$ restricts to a diffeomorphism (or biholomorphism)
$\Phi$ restricts to a diffeomorphism (or biholomorphism) ![]() $U \longrightarrow \Phi (U)$ and
$U \longrightarrow \Phi (U)$ and
This will establish that ![]() $\mathcal {H}$ is a submanifold in a neighborhood of
$\mathcal {H}$ is a submanifold in a neighborhood of ![]() $(1, \xi _0)$. The case of a general point
$(1, \xi _0)$. The case of a general point ![]() $(h_0, \xi _0)$ will be shown to follow from this special case.
$(h_0, \xi _0)$ will be shown to follow from this special case.
To prove the above-mentioned claim, let ![]() $\{U_n\}_{n \in \mathbb {N}}$ be a neighborhood basis for
$\{U_n\}_{n \in \mathbb {N}}$ be a neighborhood basis for ![]() $\mathfrak {g} \times S$ at
$\mathfrak {g} \times S$ at ![]() $(0, \xi _0)$. The differential
$(0, \xi _0)$. The differential ![]() $d\Phi _{(0, \xi _0)} : \mathfrak {g} \times T_{\xi _0} S \longrightarrow \mathfrak {g} \times T_{\xi _0} S$ is the identity map, so we may assume that
$d\Phi _{(0, \xi _0)} : \mathfrak {g} \times T_{\xi _0} S \longrightarrow \mathfrak {g} \times T_{\xi _0} S$ is the identity map, so we may assume that ![]() $\Phi$ restricts to a diffeomorphism (or biholomorphism) on each
$\Phi$ restricts to a diffeomorphism (or biholomorphism) on each ![]() $U_n$. We claim that there exists
$U_n$. We claim that there exists ![]() $n$ large enough so that
$n$ large enough so that ![]() $\Phi (U_n \cap E) = \Phi (U_n) \cap \mathcal {H}$.
$\Phi (U_n \cap E) = \Phi (U_n) \cap \mathcal {H}$.
Suppose that this is not the case. We have ![]() $\Phi (U_n \cap E) \subseteq \Phi (U_n) \cap \mathcal {H}$, so there exists
$\Phi (U_n \cap E) \subseteq \Phi (U_n) \cap \mathcal {H}$, so there exists
for all ![]() $n$. In particular,
$n$. In particular,
for some ![]() $x_n \in E_{\xi _n}$ and
$x_n \in E_{\xi _n}$ and ![]() $y_n \in F_{\xi _n}$ such that
$y_n \in F_{\xi _n}$ such that ![]() $(x_n + y_n, \xi _n) \in U_n$. As
$(x_n + y_n, \xi _n) \in U_n$. As ![]() $U_n$ is a neighborhood basis at
$U_n$ is a neighborhood basis at ![]() $(0, \xi _0)$, the sequence
$(0, \xi _0)$, the sequence ![]() $(x_n + y_n, \xi _n)$ converges to
$(x_n + y_n, \xi _n)$ converges to ![]() $(0, \xi _0)$ as
$(0, \xi _0)$ as ![]() $n \longrightarrow \infty$.
$n \longrightarrow \infty$.
Note that ![]() $y_n \neq 0$ for all
$y_n \neq 0$ for all ![]() $n$, because
$n$, because ![]() $(g_n, \xi _n) \notin \Phi (U_n \cap E)$. Fix a norm
$(g_n, \xi _n) \notin \Phi (U_n \cap E)$. Fix a norm ![]() $\|\cdot \|$ on
$\|\cdot \|$ on ![]() $\mathfrak {g}$ and set
$\mathfrak {g}$ and set ![]() $c_n = \|y_n\| > 0$. Then
$c_n = \|y_n\| > 0$. Then ![]() $c_n^{-1}y_n$ lies on the unit sphere of
$c_n^{-1}y_n$ lies on the unit sphere of ![]() $\mathfrak {g}$, so by passing to a subsequence we may assume that
$\mathfrak {g}$, so by passing to a subsequence we may assume that ![]() $c_n^{-1}y_n \longrightarrow y_0$ for some
$c_n^{-1}y_n \longrightarrow y_0$ for some ![]() $y_0 \in \mathfrak {g}$ with
$y_0 \in \mathfrak {g}$ with ![]() $\|y_0\| = 1$. Moreover,
$\|y_0\| = 1$. Moreover, ![]() $(c_n^{-1}y_n, \xi _n) \in F$ for all
$(c_n^{-1}y_n, \xi _n) \in F$ for all ![]() $n$, so
$n$, so ![]() $(y_0, \xi _0) \in F$.
$(y_0, \xi _0) \in F$.
Let ![]() $t \in \mathbb {R}$. Let
$t \in \mathbb {R}$. Let ![]() $k_n$ be the largest integer such that
$k_n$ be the largest integer such that ![]() $k_n \le t/c_n$. Then
$k_n \le t/c_n$. Then ![]() $|k_nc_n - t| \le c_n \longrightarrow 0$ and so
$|k_nc_n - t| \le c_n \longrightarrow 0$ and so ![]() $k_nc_n\longrightarrow t$. We also have
$k_nc_n\longrightarrow t$. We also have ![]() $e^{y_n} = e^{-x_n}g_n \in H_{\xi _n}$, so
$e^{y_n} = e^{-x_n}g_n \in H_{\xi _n}$, so ![]() $(e^{y_n}, \xi _n) \in \mathcal {H}$ and, hence,
$(e^{y_n}, \xi _n) \in \mathcal {H}$ and, hence,
for all ![]() $n$. As
$n$. As ![]() $\mathcal {H}$ is closed in
$\mathcal {H}$ is closed in ![]() $G \times S$, taking the limit as
$G \times S$, taking the limit as ![]() $n \longrightarrow \infty$ shows that
$n \longrightarrow \infty$ shows that ![]() $(e^{ty_0}, \xi _0) \in \mathcal {H}$, i.e.
$(e^{ty_0}, \xi _0) \in \mathcal {H}$, i.e. ![]() $e^{ty_0} \in H_{\xi _0}$. However,
$e^{ty_0} \in H_{\xi _0}$. However, ![]() $t$ is arbitrary, so we have
$t$ is arbitrary, so we have ![]() $y_0 \in E_{\xi _0}$. It follows that
$y_0 \in E_{\xi _0}$. It follows that ![]() $y_0 \in E_{\xi _0} \cap F_{\xi _0} = 0$, contradicting the fact that
$y_0 \in E_{\xi _0} \cap F_{\xi _0} = 0$, contradicting the fact that ![]() $\|y_0\| = 1$. This proves the claim, implying that
$\|y_0\| = 1$. This proves the claim, implying that ![]() $\mathcal {H}$ is a submanifold of
$\mathcal {H}$ is a submanifold of ![]() $G \times S$ in a neighborhood of
$G \times S$ in a neighborhood of ![]() $(1, \xi _0)$.
$(1, \xi _0)$.
Now let ![]() $(h_0, \xi _0) \in \mathcal {H}$ be arbitrary. Let
$(h_0, \xi _0) \in \mathcal {H}$ be arbitrary. Let ![]() $U$ be a neighborhood of
$U$ be a neighborhood of ![]() $(0, \xi _0)$ in
$(0, \xi _0)$ in ![]() $\mathfrak {g} \times S$ such that
$\mathfrak {g} \times S$ such that ![]() $\Phi$ restricts to a diffeomorphism (or biholomorphism)
$\Phi$ restricts to a diffeomorphism (or biholomorphism) ![]() $U \longrightarrow \Phi (U)$ and
$U \longrightarrow \Phi (U)$ and ![]() $\Phi (U \cap E) = \Phi (U) \cap \mathcal {H}$. As
$\Phi (U \cap E) = \Phi (U) \cap \mathcal {H}$. As ![]() $H_{\xi _0}$ is connected, we can write
$H_{\xi _0}$ is connected, we can write ![]() $h_0 = e^{x_1} \cdots e^{x_m}$ for some
$h_0 = e^{x_1} \cdots e^{x_m}$ for some ![]() $x_i \in E_{\xi _0}$. By further shrinking
$x_i \in E_{\xi _0}$. By further shrinking ![]() $S$ if necessary, we may assume that there are sections
$S$ if necessary, we may assume that there are sections ![]() $s_i : S \longrightarrow E$ for
$s_i : S \longrightarrow E$ for ![]() $i = 1, \ldots, m$ of the form
$i = 1, \ldots, m$ of the form ![]() $s_i(\xi ) = (y_i(\xi ), \xi )$, where
$s_i(\xi ) = (y_i(\xi ), \xi )$, where ![]() $y_i(\xi _0) = x_i$. Then
$y_i(\xi _0) = x_i$. Then ![]() $h(\xi ) := e^{y_1(\xi )} \cdots e^{y_m(\xi )}$ is a map
$h(\xi ) := e^{y_1(\xi )} \cdots e^{y_m(\xi )}$ is a map ![]() $S \longrightarrow G$ such that
$S \longrightarrow G$ such that ![]() $(h(\xi ), \xi ) \in \mathcal {H}$ for all
$(h(\xi ), \xi ) \in \mathcal {H}$ for all ![]() $\xi \in S$ and
$\xi \in S$ and ![]() $h(\xi _0) = h_0$. Define
$h(\xi _0) = h_0$. Define ![]() $\Psi : \mathfrak {g} \times S \longrightarrow G \times S$ to be the composition of
$\Psi : \mathfrak {g} \times S \longrightarrow G \times S$ to be the composition of ![]() $\Phi$ and the diffeomorphism (or biholomorphism)
$\Phi$ and the diffeomorphism (or biholomorphism) ![]() $G \times S \longrightarrow G \times S$ given by
$G \times S \longrightarrow G \times S$ given by ![]() $(g, \xi ) \longmapsto (h(\xi )g, \xi )$, i.e.
$(g, \xi ) \longmapsto (h(\xi )g, \xi )$, i.e.
Note that ![]() $\Psi$ is a diffeomorphism (or biholomorphism) onto its image,
$\Psi$ is a diffeomorphism (or biholomorphism) onto its image, ![]() $\Psi (U \cap E) = \Psi (U) \cap \mathcal {H}$, and
$\Psi (U \cap E) = \Psi (U) \cap \mathcal {H}$, and ![]() $\Psi (0, \xi _0) = (h_0, \xi _0)$. We conclude that
$\Psi (0, \xi _0) = (h_0, \xi _0)$. We conclude that ![]() $\mathcal {H}$ is a submanifold in a neighborhood of
$\mathcal {H}$ is a submanifold in a neighborhood of ![]() $(h_0, \xi _0)$.
$(h_0, \xi _0)$.
Remark 4.19 The assumption in Theorem 4.18 that the groups ![]() $H_\xi$ are connected can be replaced by the following more general condition: for each
$H_\xi$ are connected can be replaced by the following more general condition: for each ![]() $\xi _0 \in S$ and
$\xi _0 \in S$ and ![]() $h_0 \in H_{\xi _0}$, there is a map
$h_0 \in H_{\xi _0}$, there is a map ![]() $s$ (smooth or holomorphic) from a neighborhood of
$s$ (smooth or holomorphic) from a neighborhood of ![]() $\xi _0$ in
$\xi _0$ in ![]() $S$ to
$S$ to ![]() $G$ such that
$G$ such that ![]() $s(\xi _0) = h_0$ and
$s(\xi _0) = h_0$ and ![]() $s(\xi ) \in H_\xi$ for all
$s(\xi ) \in H_\xi$ for all ![]() $\xi$. In this case, the proof shows that
$\xi$. In this case, the proof shows that ![]() $\mathcal {H}$ is a submanifold of
$\mathcal {H}$ is a submanifold of ![]() $G \times S$ if it is closed.
$G \times S$ if it is closed.
4.5 Integration of  $G$-invariant submanifolds
$G$-invariant submanifolds
Let ![]() $G$ be a Lie group with Lie algebra
$G$ be a Lie group with Lie algebra ![]() $\mathfrak {g}$ and let
$\mathfrak {g}$ and let ![]() $S \subseteq \mathfrak {g}^{*}$ be a
$S \subseteq \mathfrak {g}^{*}$ be a ![]() $G$-invariant submanifold. Lemma 4.16 tells us that
$G$-invariant submanifold. Lemma 4.16 tells us that ![]() $S$ is a Poisson submanifold of
$S$ is a Poisson submanifold of ![]() $\mathfrak {g}^{*}$, and we let
$\mathfrak {g}^{*}$, and we let ![]() $\sigma _S:T^{*}S\longrightarrow TS$ denote the Poisson bivector field that it inherits as such. One may then attempt to find a symplectic groupoid that integrates
$\sigma _S:T^{*}S\longrightarrow TS$ denote the Poisson bivector field that it inherits as such. One may then attempt to find a symplectic groupoid that integrates ![]() $(S,\sigma _S)$, i.e. a symplectic groupoid with Lie algebroid
$(S,\sigma _S)$, i.e. a symplectic groupoid with Lie algebroid ![]() $(T^{*}S,\sigma _S:T^{*}S\longrightarrow TS)$. In what follows, we relate symplectic reduction along
$(T^{*}S,\sigma _S:T^{*}S\longrightarrow TS)$. In what follows, we relate symplectic reduction along ![]() $S$ to the process of integrating
$S$ to the process of integrating ![]() $(S, \sigma _S)$.
$(S, \sigma _S)$.
As ![]() $S$ is a Poisson submanifold, its stabilizer subalgebroid is given by
$S$ is a Poisson submanifold, its stabilizer subalgebroid is given by ![]() $L_S = TS^{\circ }$. We also know Poisson submanifolds to be stable (Lemma 4.14), so that
$L_S = TS^{\circ }$. We also know Poisson submanifolds to be stable (Lemma 4.14), so that
is a Lie subalgebra of ![]() $\mathfrak {g}$ for all
$\mathfrak {g}$ for all ![]() $\xi \in S$. Let
$\xi \in S$. Let ![]() $H_\xi \subseteq G$ be the connected Lie subgroup of
$H_\xi \subseteq G$ be the connected Lie subgroup of ![]() $G$ with Lie algebra
$G$ with Lie algebra ![]() $\mathfrak {h}_\xi$ and suppose that
$\mathfrak {h}_\xi$ and suppose that
is a submanifold of ![]() $T^{*}G$. It follows from Theorem 4.17(iii) that
$T^{*}G$. It follows from Theorem 4.17(iii) that ![]() $\mathcal {H}$ is a source-connected stabilizer subgroupoid of
$\mathcal {H}$ is a source-connected stabilizer subgroupoid of ![]() $S$ in
$S$ in ![]() $T^{*}G \rightrightarrows \mathfrak {g}^{*}$. Suppose also that
$T^{*}G \rightrightarrows \mathfrak {g}^{*}$. Suppose also that ![]() $(S, \mathcal {H})$ is a clean reduction datum for the action of
$(S, \mathcal {H})$ is a clean reduction datum for the action of ![]() $G$ on
$G$ on ![]() $T^{*}G$ by right translations, so that the universal reduced space
$T^{*}G$ by right translations, so that the universal reduced space
described in § 4.3 is a Hamiltonian ![]() $G$-space. Note that if
$G$-space. Note that if ![]() $\mathcal {H}$ is closed in
$\mathcal {H}$ is closed in ![]() $G \times S$, then
$G \times S$, then ![]() $\mathcal {H}$ is a submanifold of
$\mathcal {H}$ is a submanifold of ![]() $T^{*}G$ (Theorem 4.17(iv)) and
$T^{*}G$ (Theorem 4.17(iv)) and ![]() $(S,\mathcal {H})$ is clean (Lemma 4.3).
$(S,\mathcal {H})$ is clean (Lemma 4.3).
Remark 4.20 The stabilizer subgroupoid (4.9) of a ![]() $G$-invariant submanifold
$G$-invariant submanifold ![]() $S \subseteq \mathfrak {g}^{*}$ has been studied as a so-called character Lagrangian. We refer the reader to [Reference WeinsteinWei82], [Reference Guillemin and SternbergGS82b, Eq. (4.5)], [Reference Guillemin and SternbergGS83], and [Reference Guillemin and SternbergGS13, § 12.5] for further details.
$S \subseteq \mathfrak {g}^{*}$ has been studied as a so-called character Lagrangian. We refer the reader to [Reference WeinsteinWei82], [Reference Guillemin and SternbergGS82b, Eq. (4.5)], [Reference Guillemin and SternbergGS83], and [Reference Guillemin and SternbergGS13, § 12.5] for further details.
Theorem 4.21 (Theorem D(iv))
Let ![]() $S\subseteq \mathfrak {g}^{*}$ be a
$S\subseteq \mathfrak {g}^{*}$ be a ![]() $G$-invariant submanifold. Assume that (4.9) is a submanifold of
$G$-invariant submanifold. Assume that (4.9) is a submanifold of ![]() $T^{*}G$ and that
$T^{*}G$ and that ![]() $(S,\mathcal {H})$ is a clean reduction datum for the action of
$(S,\mathcal {H})$ is a clean reduction datum for the action of ![]() $G$ on
$G$ on ![]() $T^{*}G$ by right translations. The symplectic manifold
$T^{*}G$ by right translations. The symplectic manifold ![]() $\mathfrak {M}_{G, S}$ then has the structure of a symplectic groupoid integrating
$\mathfrak {M}_{G, S}$ then has the structure of a symplectic groupoid integrating ![]() $(S, \sigma _S)$. The underlying source and target maps are given by
$(S, \sigma _S)$. The underlying source and target maps are given by
Proof. Note that ![]() $\mathcal {H}$ is a Lie subgroupoid of
$\mathcal {H}$ is a Lie subgroupoid of ![]() $G \times S = (T^{*}G)\vert _S$. Hence, to give
$G \times S = (T^{*}G)\vert _S$. Hence, to give
the structure of a Lie groupoid over ![]() $S$, it suffices to show that
$S$, it suffices to show that ![]() $\mathcal {H}$ is normal in
$\mathcal {H}$ is normal in ![]() $G \times S$. This amounts to checking that
$G \times S$. This amounts to checking that ![]() $(ghg^{-1}, \mathrm {Ad}_g^{*}\xi ) \in \mathcal {H}$ for all
$(ghg^{-1}, \mathrm {Ad}_g^{*}\xi ) \in \mathcal {H}$ for all ![]() $g \in G$ and
$g \in G$ and ![]() $(h, \xi ) \in \mathcal {H}$. In other words, we want to show that
$(h, \xi ) \in \mathcal {H}$. In other words, we want to show that
Note that ![]() $G$-invariance of
$G$-invariance of ![]() $S$ yields
$S$ yields ![]() $\mathrm {Ad}_g^{*}(T_\xi S) = T_{\mathrm {Ad}_g^{*}\xi } S$, so
$\mathrm {Ad}_g^{*}(T_\xi S) = T_{\mathrm {Ad}_g^{*}\xi } S$, so
We conclude that ![]() $\mathrm {Ad}_g \mathfrak {h}_\xi = \mathfrak {h}_{\mathrm {Ad}_g^{*}\xi }$, and (4.11) now results from connectedness of
$\mathrm {Ad}_g \mathfrak {h}_\xi = \mathfrak {h}_{\mathrm {Ad}_g^{*}\xi }$, and (4.11) now results from connectedness of ![]() $H_\xi$. It follows that
$H_\xi$. It follows that ![]() $\mathfrak {M}$ is a Lie groupoid with source and target maps given by (4.10).
$\mathfrak {M}$ is a Lie groupoid with source and target maps given by (4.10).
Let ![]() $\Gamma _{\mathfrak {M}} \subseteq \mathfrak {M} \times \mathfrak {M} \times \mathfrak {M}$ be the graph of multiplication in
$\Gamma _{\mathfrak {M}} \subseteq \mathfrak {M} \times \mathfrak {M} \times \mathfrak {M}$ be the graph of multiplication in ![]() $\mathfrak {M}$. Similarly, let
$\mathfrak {M}$. Similarly, let ![]() $\mathcal {G} := T^{*}G$ and let
$\mathcal {G} := T^{*}G$ and let ![]() $\Gamma _\mathcal {G}$ be its graph of multiplication. Recall that
$\Gamma _\mathcal {G}$ be its graph of multiplication. Recall that ![]() $\Gamma _\mathcal {G}$ is Lagrangian in
$\Gamma _\mathcal {G}$ is Lagrangian in ![]() $\mathcal {G} \times \mathcal {G} \times \mathcal {G}^{-}$ by assumption. We have
$\mathcal {G} \times \mathcal {G} \times \mathcal {G}^{-}$ by assumption. We have
where ![]() $\pi : G \times S \longrightarrow {\mathfrak {M}}$ is the quotient map. On the other hand, let
$\pi : G \times S \longrightarrow {\mathfrak {M}}$ is the quotient map. On the other hand, let ![]() $\bar {\omega }$ and
$\bar {\omega }$ and ![]() $\omega$ be the symplectic forms on
$\omega$ be the symplectic forms on ![]() ${\mathfrak {M}} \times {\mathfrak {M}} \times {\mathfrak {M}}^{-}$ and
${\mathfrak {M}} \times {\mathfrak {M}} \times {\mathfrak {M}}^{-}$ and ![]() $\mathcal {G} \times \mathcal {G} \times \mathcal {G}^{-}$, respectively. Note that for all
$\mathcal {G} \times \mathcal {G} \times \mathcal {G}^{-}$, respectively. Note that for all ![]() $u_1, u_2 \in T\Gamma _{\mathfrak {M}}$, we have
$u_1, u_2 \in T\Gamma _{\mathfrak {M}}$, we have ![]() $u_i = d\pi (v_i)$ for some
$u_i = d\pi (v_i)$ for some ![]() $v_i \in T\Gamma _\mathcal {G}$ and, hence,
$v_i \in T\Gamma _\mathcal {G}$ and, hence,
It follows that ![]() $\Gamma _{\mathfrak {M}}$ is Lagrangian in
$\Gamma _{\mathfrak {M}}$ is Lagrangian in ![]() $\mathfrak {M} \times \mathfrak {M} \times \mathfrak {M}^{-}$, so that
$\mathfrak {M} \times \mathfrak {M} \times \mathfrak {M}^{-}$, so that ![]() $\mathfrak {M}$ is a symplectic groupoid.
$\mathfrak {M}$ is a symplectic groupoid.
Note also that ![]() $\mathcal {H}$ acts trivially on
$\mathcal {H}$ acts trivially on ![]() $S$, as
$S$, as ![]() $H_\xi$ is contained in the
$H_\xi$ is contained in the ![]() $G$-stabilizer of
$G$-stabilizer of ![]() $\xi$ for all
$\xi$ for all ![]() $\xi \in S$. Theorem 2.24 or Theorem 3.16 then implies that the source map
$\xi \in S$. Theorem 2.24 or Theorem 3.16 then implies that the source map ![]() $\mathsf {s} : T^{*}G \longrightarrow \mathfrak {g}^{*}$ descends to a Poisson map
$\mathsf {s} : T^{*}G \longrightarrow \mathfrak {g}^{*}$ descends to a Poisson map ![]() ${\mathfrak {M}} \longrightarrow S$. We conclude that
${\mathfrak {M}} \longrightarrow S$. We conclude that ![]() ${\mathfrak {M}}$ integrates
${\mathfrak {M}}$ integrates ![]() $(S, \sigma _S)$.
$(S, \sigma _S)$.
Remark 4.22 The assumption that the groups ![]() $H_\xi$ are connected can be omitted if (4.11) holds.
$H_\xi$ are connected can be omitted if (4.11) holds.
Example 4.23 Let ![]() $G$ be a compact Lie group with Lie algebra
$G$ be a compact Lie group with Lie algebra ![]() $\mathfrak {g}$ and choose a
$\mathfrak {g}$ and choose a ![]() $G$-invariant inner product
$G$-invariant inner product ![]() $\langle {\cdot }\,{,}\,{\cdot }\rangle :\mathfrak {g}\otimes _{\mathbb {R}}\mathfrak {g}\longrightarrow \mathbb {R}$. This induces an inner product on
$\langle {\cdot }\,{,}\,{\cdot }\rangle :\mathfrak {g}\otimes _{\mathbb {R}}\mathfrak {g}\longrightarrow \mathbb {R}$. This induces an inner product on ![]() $\mathfrak {g}^{*}$, in which context one has the Lie–Poisson sphere [Reference MarcutMar14]
$\mathfrak {g}^{*}$, in which context one has the Lie–Poisson sphere [Reference MarcutMar14]
Note that ![]() $(T_\xi \mathbb {S}(\mathfrak {g}^{*}))^{\circ } = \mathbb {R} \xi _*$ for all
$(T_\xi \mathbb {S}(\mathfrak {g}^{*}))^{\circ } = \mathbb {R} \xi _*$ for all ![]() $\xi \in \mathbb {S}(\mathfrak {g}^{*})$, where
$\xi \in \mathbb {S}(\mathfrak {g}^{*})$, where ![]() $\xi _*$ is the unique element of
$\xi _*$ is the unique element of ![]() $\mathfrak {g}$ satisfying
$\mathfrak {g}$ satisfying ![]() $\langle \xi _*, \cdot \rangle = \xi$. It follows that the stabilizer subgroupoid (4.9) of
$\langle \xi _*, \cdot \rangle = \xi$. It follows that the stabilizer subgroupoid (4.9) of ![]() $\mathbb {S}(\mathfrak {g}^{*})$ is of the form
$\mathbb {S}(\mathfrak {g}^{*})$ is of the form
Note that ![]() $\mathcal {H}$ is closed in
$\mathcal {H}$ is closed in ![]() $T^{*}G|_{\mathbb {S}(\mathfrak {g}^{*})}$ if and only if
$T^{*}G|_{\mathbb {S}(\mathfrak {g}^{*})}$ if and only if ![]() $\mathfrak {g} = \mathfrak {su}(2)$. Indeed, in rank higher than one, almost all fibers of
$\mathfrak {g} = \mathfrak {su}(2)$. Indeed, in rank higher than one, almost all fibers of ![]() $\mathcal {H}$ are dense lines on tori. This is consistent with the fact that
$\mathcal {H}$ are dense lines on tori. This is consistent with the fact that ![]() $\mathbb {S}(\mathfrak {g}^{*})$ is integrable to a symplectic groupoid if and only if
$\mathbb {S}(\mathfrak {g}^{*})$ is integrable to a symplectic groupoid if and only if ![]() $\mathfrak {g} = \mathfrak {su}(2)$ (see [Reference MarcutMar14]). If
$\mathfrak {g} = \mathfrak {su}(2)$ (see [Reference MarcutMar14]). If ![]() $G = \mathrm {SU}(2)$, then
$G = \mathrm {SU}(2)$, then ![]() $\mathbb {S}(\mathfrak {g}^{*}) = S^{2}$ is a symplectic leaf and
$\mathbb {S}(\mathfrak {g}^{*}) = S^{2}$ is a symplectic leaf and
is its canonical integration. This is a straightforward consequence of Lemma 4.25 in the next subsection.
4.6 Symplectic reduction along a coadjoint orbit
Let ![]() $(M, \omega )$ be symplectic manifold and
$(M, \omega )$ be symplectic manifold and ![]() $G$ a Lie group acting on
$G$ a Lie group acting on ![]() $M$ in a Hamiltonian way with moment map
$M$ in a Hamiltonian way with moment map ![]() $\mu : M \longrightarrow \mathfrak {g}^{*}$. We now describe the symplectic reduction of
$\mu : M \longrightarrow \mathfrak {g}^{*}$. We now describe the symplectic reduction of ![]() $M$ by
$M$ by ![]() $G$ along a coadjoint orbit
$G$ along a coadjoint orbit ![]() $\mathcal {O} \subseteq \mathfrak {g}^{*}$.
$\mathcal {O} \subseteq \mathfrak {g}^{*}$.
Lemma 4.24 The coadjoint orbit ![]() $\mathcal {O}\subseteq \mathfrak {g}^{*}$ is pre-Poisson and
$\mathcal {O}\subseteq \mathfrak {g}^{*}$ is pre-Poisson and
is a stabilizer subgroupoid of ![]() $\mathcal {O}$ in
$\mathcal {O}$ in ![]() $T^{*}G$.
$T^{*}G$.
Proof. Lemma 4.16 implies that ![]() $\mathcal {O}$ is a stable pre-Poisson submanifold of
$\mathcal {O}$ is a stable pre-Poisson submanifold of ![]() $\mathfrak {g}^{*}$. Note that for all
$\mathfrak {g}^{*}$. Note that for all ![]() $\xi \in \mathcal {O}$ we have
$\xi \in \mathcal {O}$ we have ![]() $(T_\xi \mathcal {O})^{\circ } = \mathfrak {g}_\xi$, so the Lie subalgebra
$(T_\xi \mathcal {O})^{\circ } = \mathfrak {g}_\xi$, so the Lie subalgebra ![]() $\mathfrak {h}_\xi := (T_\xi \mathcal {O})^{\circ } \cap \mathfrak {g}_\xi$ of
$\mathfrak {h}_\xi := (T_\xi \mathcal {O})^{\circ } \cap \mathfrak {g}_\xi$ of ![]() $\mathfrak {g}$ considered in (4.8) is
$\mathfrak {g}$ considered in (4.8) is ![]() $\mathfrak {g}_\xi$. By Theorem 4.17(ii), it suffices to check that
$\mathfrak {g}_\xi$. By Theorem 4.17(ii), it suffices to check that ![]() $\mathcal {H}$ is isotropic in
$\mathcal {H}$ is isotropic in ![]() $T^{*}G$. To this end, we first compute the tangent space of
$T^{*}G$. To this end, we first compute the tangent space of ![]() $\mathcal {H}$ at a general point. Consider the map
$\mathcal {H}$ at a general point. Consider the map
noting that ![]() $T_{(g, \xi )}\mathcal {H} = \ker d\varphi _{(g, \xi )}$. Note also that any vector in
$T_{(g, \xi )}\mathcal {H} = \ker d\varphi _{(g, \xi )}$. Note also that any vector in ![]() $T_{(g, \xi )}(G \times \mathcal {O})$ is of the form
$T_{(g, \xi )}(G \times \mathcal {O})$ is of the form ![]() $(u, \mathrm {ad}_v^{*}\xi )$ for some
$(u, \mathrm {ad}_v^{*}\xi )$ for some ![]() $u, v \in \mathfrak {g}$. We then have
$u, v \in \mathfrak {g}$. We then have
so that
Let ![]() $(u_i, \mathrm {ad}_{v_i}^{*}\xi )$ for
$(u_i, \mathrm {ad}_{v_i}^{*}\xi )$ for ![]() $i \in \{1, 2\}$ be two such vectors. By (4.1), we have
$i \in \{1, 2\}$ be two such vectors. By (4.1), we have
The first term of (4.13) is
and a similar computation shows that the second term is
The third term of (4.13) is
 \begin{align*} -\xi([u_1, u_2]) &= (\mathrm{ad}_{u_1}^{*}\xi)(u_2) \\ &= (\mathrm{Ad}_{g^{-1}}^{*} - 1)(\mathrm{ad}_{v_1}^{*}\xi)(u_2) \\ &= \xi([\mathrm{Ad}_g u_2, v_1]) + \xi([v_1, u_2]) \\ &= \xi([u_2, \mathrm{Ad}_{g^{-1}}v_1]) - \xi([u_2, v_1]) \\ &= (\mathrm{ad}_{u_2}^{*}\xi)(-\mathrm{Ad}_{g^{-1}}v_1 + v_1) \\ &= (\mathrm{Ad}_{g^{-1}}^{*} - 1)(\mathrm{ad}_{v_2}^{*}\xi)(-\mathrm{Ad}_{g^{-1}}v_1 + v_1) \\ &= -\xi([v_1, v_2] + [v_2, \mathrm{Ad}_g v_1] + [v_2, \mathrm{Ad}_{g^{-1}}v_1] + [v_1, v_2]) \\ &= -\xi(2[v_1, v_2] + [v_2, \mathrm{Ad}_g v_1] + [\mathrm{Ad}_g v_2, v_1]). \end{align*}
\begin{align*} -\xi([u_1, u_2]) &= (\mathrm{ad}_{u_1}^{*}\xi)(u_2) \\ &= (\mathrm{Ad}_{g^{-1}}^{*} - 1)(\mathrm{ad}_{v_1}^{*}\xi)(u_2) \\ &= \xi([\mathrm{Ad}_g u_2, v_1]) + \xi([v_1, u_2]) \\ &= \xi([u_2, \mathrm{Ad}_{g^{-1}}v_1]) - \xi([u_2, v_1]) \\ &= (\mathrm{ad}_{u_2}^{*}\xi)(-\mathrm{Ad}_{g^{-1}}v_1 + v_1) \\ &= (\mathrm{Ad}_{g^{-1}}^{*} - 1)(\mathrm{ad}_{v_2}^{*}\xi)(-\mathrm{Ad}_{g^{-1}}v_1 + v_1) \\ &= -\xi([v_1, v_2] + [v_2, \mathrm{Ad}_g v_1] + [v_2, \mathrm{Ad}_{g^{-1}}v_1] + [v_1, v_2]) \\ &= -\xi(2[v_1, v_2] + [v_2, \mathrm{Ad}_g v_1] + [\mathrm{Ad}_g v_2, v_1]). \end{align*}By combining the last three expressions with (4.13), we obtain
Note that ![]() $\mathcal {H}$ is closed in
$\mathcal {H}$ is closed in ![]() $T^{*}G\vert _\mathcal {O}$. Proposition 4.10 therefore implies that
$T^{*}G\vert _\mathcal {O}$. Proposition 4.10 therefore implies that
is a Hamiltonian ![]() $G$-space.
$G$-space.
Lemma 4.25 There is a canonical symplectomorphism
and it is equivariant for the Hamiltonian ![]() $G$-action on
$G$-action on ![]() $\mathfrak {M}_{G, \mathcal {O}, \mathcal {H}}$ and the
$\mathfrak {M}_{G, \mathcal {O}, \mathcal {H}}$ and the ![]() $G$-action on the first factor of
$G$-action on the first factor of ![]() $\mathcal {O} \times \mathcal {O}^{-}$.
$\mathcal {O} \times \mathcal {O}^{-}$.
Proof. We have ![]() $\mathfrak {M}_{G, \mathcal {O}, \mathcal {H}} = (G \times \mathcal {O}) / {\sim }$, where
$\mathfrak {M}_{G, \mathcal {O}, \mathcal {H}} = (G \times \mathcal {O}) / {\sim }$, where ![]() $(g, \xi ) \sim (gh^{-1}, \xi )$ for all
$(g, \xi ) \sim (gh^{-1}, \xi )$ for all ![]() $(g, \xi ) \in G \times \mathcal {O}$ and
$(g, \xi ) \in G \times \mathcal {O}$ and ![]() ${h \in G_\xi}$. This implies that the map
${h \in G_\xi}$. This implies that the map
descends to a diffeomorphism ![]() $\mathfrak {M}_{G, \mathcal {O}, \mathcal {H}} \cong \mathcal {O} \times \mathcal {O}^{-}$. To show that it is a symplectomorphism, we need to show that
$\mathfrak {M}_{G, \mathcal {O}, \mathcal {H}} \cong \mathcal {O} \times \mathcal {O}^{-}$. To show that it is a symplectomorphism, we need to show that ![]() $\psi ^{*}(\beta, -\beta ) = i^{*}\Omega,$ where
$\psi ^{*}(\beta, -\beta ) = i^{*}\Omega,$ where ![]() $\beta \in \Omega _{\mathcal {O}}^{2}$ is the Kirillov–Kostant–Souriau symplectic form on
$\beta \in \Omega _{\mathcal {O}}^{2}$ is the Kirillov–Kostant–Souriau symplectic form on ![]() $\mathcal {O}$,
$\mathcal {O}$, ![]() $i$ is the inclusion
$i$ is the inclusion ![]() $G \times \mathcal {O} \hookrightarrow T^{*}G = G \times \mathfrak {g}^{*}$, and
$G \times \mathcal {O} \hookrightarrow T^{*}G = G \times \mathfrak {g}^{*}$, and ![]() $\Omega$ is the canonical symplectic form on
$\Omega$ is the canonical symplectic form on ![]() $T^{*}G$.
$T^{*}G$.
Observe that we have a short exact sequence
where the map ![]() $\mathfrak {g} \longrightarrow T_\xi \mathcal {O}$ is given by
$\mathfrak {g} \longrightarrow T_\xi \mathcal {O}$ is given by ![]() $x \longmapsto \mathrm {ad}_x^{*}\xi$. Observe also that
$x \longmapsto \mathrm {ad}_x^{*}\xi$. Observe also that ![]() $\beta$ is characterized by the condition
$\beta$ is characterized by the condition
for all ![]() $x,y\in \mathfrak {g}$. We then find that
$x,y\in \mathfrak {g}$. We then find that
so
 \begin{align*} \psi^{*}(\beta, -\beta)_{(g, \xi)}((x, \mathrm{ad}_y^{*}\xi), (u, \mathrm{ad}_v^{*}\xi)) &= -(\mathrm{Ad}_g^{*}\xi)([\mathrm{Ad}_g(x+y), \mathrm{Ad}_g(u+v)]) + \xi([y, u])\\ &= -\xi([x+y,u+v]) + \xi([y,v]) \\ &= -\xi([x, u] + [x, v] + [y, u]). \end{align*}
\begin{align*} \psi^{*}(\beta, -\beta)_{(g, \xi)}((x, \mathrm{ad}_y^{*}\xi), (u, \mathrm{ad}_v^{*}\xi)) &= -(\mathrm{Ad}_g^{*}\xi)([\mathrm{Ad}_g(x+y), \mathrm{Ad}_g(u+v)]) + \xi([y, u])\\ &= -\xi([x+y,u+v]) + \xi([y,v]) \\ &= -\xi([x, u] + [x, v] + [y, u]). \end{align*}On the other hand,
 \begin{align*} \Omega_{(g, \xi)}((x, \mathrm{ad}_y^{*}\xi), (u, \mathrm{ad}_v^{*}\xi)) &= -\mathrm{ad}_v^{*}\xi(x) + \mathrm{ad}_y^{*}\xi(u) - \xi([x, u]) \\ &= -\xi([x, u] + [x, v] + [y, u]). \end{align*}
\begin{align*} \Omega_{(g, \xi)}((x, \mathrm{ad}_y^{*}\xi), (u, \mathrm{ad}_v^{*}\xi)) &= -\mathrm{ad}_v^{*}\xi(x) + \mathrm{ad}_y^{*}\xi(u) - \xi([x, u]) \\ &= -\xi([x, u] + [x, v] + [y, u]). \end{align*}
It follows that ![]() $\psi ^{*}(\beta, -\beta ) = i^{*}\Omega$.
$\psi ^{*}(\beta, -\beta ) = i^{*}\Omega$.
The symplectic reduction ![]() $M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{\mathcal {O}, \mathcal {H}}} G$ of
$M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{\mathcal {O}, \mathcal {H}}} G$ of ![]() $M$ by
$M$ by ![]() $G$ along
$G$ along ![]() $\mathcal {O}$ with respect to (4.12) is not necessarily
$\mathcal {O}$ with respect to (4.12) is not necessarily ![]() $\mu ^{-1}(\mathcal {O}) / G$ (see [Reference Kazhdan, Kostant and SternbergKKS78]), but the two are closely related.
$\mu ^{-1}(\mathcal {O}) / G$ (see [Reference Kazhdan, Kostant and SternbergKKS78]), but the two are closely related.
Proposition 4.26 (Theorem F(i))
Let ![]() $\mathcal {H}$ be defined by (4.12) and suppose that
$\mathcal {H}$ be defined by (4.12) and suppose that ![]() $(\mathcal {O}, \mathcal {H})$ is a clean reduction datum for the action of
$(\mathcal {O}, \mathcal {H})$ is a clean reduction datum for the action of ![]() $G$ on
$G$ on ![]() $M$. Then there is a canonical symplectomorphism
$M$. Then there is a canonical symplectomorphism
Proof. By Theorem 4.11, this is a consequence of Lemma 4.25 and the ‘shifting trick’ ![]() $(M \times \mathcal {O}) \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{0}} G \cong \mu ^{-1}(\mathcal {O}) / G$.
$(M \times \mathcal {O}) \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{0}} G \cong \mu ^{-1}(\mathcal {O}) / G$.
Remark 4.27 As will be explained in forthcoming work of Bălibanu and Mayrand, one can obtain the usual Hamiltonian reduction ![]() $\mu ^{-1}(\mathcal {O})/G$ directly by taking the quotient by the action groupoid
$\mu ^{-1}(\mathcal {O})/G$ directly by taking the quotient by the action groupoid ![]() $G \times \mathcal {O} \rightrightarrows \mathcal {O}$ instead of
$G \times \mathcal {O} \rightrightarrows \mathcal {O}$ instead of ![]() $\mathcal {H}$.
$\mathcal {H}$.
4.7 Symplectic implosion
The following subsection only applies to the smooth category.
Let ![]() $K$ be a compact connected Lie group with Lie algebra
$K$ be a compact connected Lie group with Lie algebra ![]() $\mathfrak {k}$. Let us also fix a maximal torus
$\mathfrak {k}$. Let us also fix a maximal torus ![]() $T\subseteq K$ with Lie algebra
$T\subseteq K$ with Lie algebra ![]() $\mathfrak {t}\subseteq \mathfrak {k}$. Write
$\mathfrak {t}\subseteq \mathfrak {k}$. Write ![]() $\Phi \subseteq (i\mathfrak {t})^{*}$ for the associated set of roots and let
$\Phi \subseteq (i\mathfrak {t})^{*}$ for the associated set of roots and let ![]() $\alpha ^{\vee }\in i\mathfrak {t}$ denote the coroot determined by
$\alpha ^{\vee }\in i\mathfrak {t}$ denote the coroot determined by ![]() $\alpha \in \Phi$. Choose a closed fundamental Weyl chamber
$\alpha \in \Phi$. Choose a closed fundamental Weyl chamber ![]() $\mathfrak {t}_+^{*} \subseteq \mathfrak {t}^{*}$ and let
$\mathfrak {t}_+^{*} \subseteq \mathfrak {t}^{*}$ and let ![]() $\Delta \subseteq \Phi$ be the induced set of simple roots, i.e.
$\Delta \subseteq \Phi$ be the induced set of simple roots, i.e.
The faces of ![]() $\mathfrak {t}_+^{*}$ are in one-to-one correspondence with the subsets
$\mathfrak {t}_+^{*}$ are in one-to-one correspondence with the subsets ![]() $\sigma$ of
$\sigma$ of ![]() $\Delta$ via
$\Delta$ via
If ![]() $S \subseteq \mathfrak {t}_+^{*}$ is a face, then the
$S \subseteq \mathfrak {t}_+^{*}$ is a face, then the ![]() $K$-stabilizers
$K$-stabilizers ![]() $K_{\xi }$ and
$K_{\xi }$ and ![]() $K_{\eta }$ coincide for all
$K_{\eta }$ coincide for all ![]() $\xi,\eta \in S$; we write
$\xi,\eta \in S$; we write ![]() $K_S$ for this common stabilizer.
$K_S$ for this common stabilizer.
Lemma 4.28 Let ![]() $S \subseteq \mathfrak {t}_+^{*}$ be a face. Then
$S \subseteq \mathfrak {t}_+^{*}$ be a face. Then ![]() $S$ is a pre-Poisson submanifold of
$S$ is a pre-Poisson submanifold of ![]() $\mathfrak {k}^{*}$ and
$\mathfrak {k}^{*}$ and
is a stabilizer subgroupoid of ![]() $S$ in
$S$ in ![]() $T^{*}K = K \times \mathfrak {k}^{*}$.
$T^{*}K = K \times \mathfrak {k}^{*}$.
Proof. Note that ![]() $[K_S, K_S]$ is the connected Lie subgroup of
$[K_S, K_S]$ is the connected Lie subgroup of ![]() $G$ with Lie algebra
$G$ with Lie algebra ![]() $[\mathfrak {k}_S, \mathfrak {k}_S]$. This combines with Lemma 4.5(iii) and reduces us to showing the following: for all
$[\mathfrak {k}_S, \mathfrak {k}_S]$. This combines with Lemma 4.5(iii) and reduces us to showing the following: for all ![]() $\xi \in S$, the Lie algebroid fiber
$\xi \in S$, the Lie algebroid fiber
is equal to ![]() $[\mathfrak {k}_\xi, \mathfrak {k}_\xi ]$.
$[\mathfrak {k}_\xi, \mathfrak {k}_\xi ]$.
Identify ![]() $\mathfrak {k}$ with
$\mathfrak {k}$ with ![]() $\mathfrak {k}^{*}$ via a
$\mathfrak {k}^{*}$ via a ![]() $K$-invariant inner product
$K$-invariant inner product ![]() $\langle {\cdot }\,{,}\,{\cdot }\rangle :\mathfrak {k}\otimes _{\mathbb {R}}\mathfrak {k}\longrightarrow \mathbb {R}$, and let
$\langle {\cdot }\,{,}\,{\cdot }\rangle :\mathfrak {k}\otimes _{\mathbb {R}}\mathfrak {k}\longrightarrow \mathbb {R}$, and let ![]() $y \in \mathfrak {k}$ be the element corresponding to
$y \in \mathfrak {k}$ be the element corresponding to ![]() $\xi \in S$. Then
$\xi \in S$. Then ![]() $T_\xi S$ corresponds to the intersection of all root hyperplanes containing
$T_\xi S$ corresponds to the intersection of all root hyperplanes containing ![]() $y$, i.e. to
$y$, i.e. to
 \begin{align*} V_y := \bigcap_{\substack{\alpha \in \Phi \\ \alpha(y) = 0}} \ker \alpha. \end{align*}
\begin{align*} V_y := \bigcap_{\substack{\alpha \in \Phi \\ \alpha(y) = 0}} \ker \alpha. \end{align*}It therefore suffices to show that
is equal to ![]() $[\mathfrak {k}_y, \mathfrak {k}_y]$.
$[\mathfrak {k}_y, \mathfrak {k}_y]$.
Note that if ![]() $x \in L_y$, then
$x \in L_y$, then
so, in fact, ![]() $L_y = V_y^{\perp } \cap \mathfrak {k}_y$. On the other hand, consider the complexifications
$L_y = V_y^{\perp } \cap \mathfrak {k}_y$. On the other hand, consider the complexifications ![]() $\mathfrak {g} := \mathfrak {k}_\mathbb {C}$ and
$\mathfrak {g} := \mathfrak {k}_\mathbb {C}$ and ![]() $\mathfrak {h} := \mathfrak {t}_\mathbb {C}$ of
$\mathfrak {h} := \mathfrak {t}_\mathbb {C}$ of ![]() $\mathfrak {k}$ and
$\mathfrak {k}$ and ![]() $\mathfrak {t}$, respectively. Then
$\mathfrak {t}$, respectively. Then ![]() $(V_y)_\mathbb {C}$ is the intersection of
$(V_y)_\mathbb {C}$ is the intersection of ![]() $\ker \alpha$ for all roots
$\ker \alpha$ for all roots ![]() $\alpha : \mathfrak {h} \longrightarrow \mathbb {C}$ such that
$\alpha : \mathfrak {h} \longrightarrow \mathbb {C}$ such that ![]() $\alpha (y) = 0$. In light of this, it suffices to show that
$\alpha (y) = 0$. In light of this, it suffices to show that
Let
One sees that ![]() $\Psi$ is a closed root subsystem of
$\Psi$ is a closed root subsystem of ![]() $\Phi$. It therefore determines a semisimple subalgebra [Reference DynkinDyn52]:
$\Phi$. It therefore determines a semisimple subalgebra [Reference DynkinDyn52]:
where ![]() $\mathfrak {h}_\Psi$ is the span of the coroots
$\mathfrak {h}_\Psi$ is the span of the coroots ![]() $\alpha ^{\vee }$ for all
$\alpha ^{\vee }$ for all ![]() $\alpha \in \Psi$ (see e.g. [Reference Vinberg, Gorbatsevich and OnishchikVGO90, Chapter 6, § 1]). Note that
$\alpha \in \Psi$ (see e.g. [Reference Vinberg, Gorbatsevich and OnishchikVGO90, Chapter 6, § 1]). Note that
so ![]() $[\mathfrak {g}_y, \mathfrak {g}_y] = \mathfrak {g}_\Psi$. We also have
$[\mathfrak {g}_y, \mathfrak {g}_y] = \mathfrak {g}_\Psi$. We also have
so ![]() $(V_y)_\mathbb {C}^{\perp } \cap \mathfrak {g}_y = \mathfrak {g}_\Psi = [\mathfrak {g}_y, \mathfrak {g}_y]$. Our proof is therefore complete.
$(V_y)_\mathbb {C}^{\perp } \cap \mathfrak {g}_y = \mathfrak {g}_\Psi = [\mathfrak {g}_y, \mathfrak {g}_y]$. Our proof is therefore complete.
Now let ![]() $K$ act on a symplectic manifold
$K$ act on a symplectic manifold ![]() $(M, \omega )$ in a Hamiltonian way with moment map
$(M, \omega )$ in a Hamiltonian way with moment map ![]() $\mu : M \longrightarrow \mathfrak {k}^{*}$. Recall that the imploded cross-section of
$\mu : M \longrightarrow \mathfrak {k}^{*}$. Recall that the imploded cross-section of ![]() $M$ (see [Reference Guillemin, Jeffrey and SjamaarGJS02]) is the quotient topological space
$M$ (see [Reference Guillemin, Jeffrey and SjamaarGJS02]) is the quotient topological space
where ![]() $p \sim q$ if
$p \sim q$ if ![]() $p = k \cdot q$ for some
$p = k \cdot q$ for some ![]() $k \in [K_{\mu (p)}, K_{\mu (p)}]$. This space can also be written as the disjoint union
$k \in [K_{\mu (p)}, K_{\mu (p)}]$. This space can also be written as the disjoint union
where each piece ![]() $\mu ^{-1}(S_\sigma ) / [K_{S_\sigma }, K_{S_\sigma }]$ is a symplectic manifold. By Lemma 4.28 and the fact that the groups
$\mu ^{-1}(S_\sigma ) / [K_{S_\sigma }, K_{S_\sigma }]$ is a symplectic manifold. By Lemma 4.28 and the fact that the groups ![]() $[K_S, K_S]$ in (4.14) are connected, we obtain the following result.
$[K_S, K_S]$ in (4.14) are connected, we obtain the following result.
Proposition 4.29 (Theorem F(ii))
The symplectic reduction of ![]() $M$ by
$M$ by ![]() $K$ along
$K$ along ![]() $\mathfrak {t}_+^{*}$ is the imploded cross-section of
$\mathfrak {t}_+^{*}$ is the imploded cross-section of ![]() $M$ by
$M$ by ![]() $K$, i.e.
$K$, i.e.
Remark 4.30 Although the subset ![]() $\mathfrak {t}_+^{*} \subseteq \mathfrak {k}^{*}$ is not a submanifold, we define the quotient as in Remark 2.17.
$\mathfrak {t}_+^{*} \subseteq \mathfrak {k}^{*}$ is not a submanifold, we define the quotient as in Remark 2.17.
Remark 4.31 Proposition 4.29 shows that the universal reduced space ![]() $\mathfrak {M}_{K, \mathfrak {t}_+^{*}}$ is the universal imploded cross-section
$\mathfrak {M}_{K, \mathfrak {t}_+^{*}}$ is the universal imploded cross-section ![]() $(T^{*}K)_{\mathrm {impl}}$ (see [Reference Guillemin, Jeffrey and SjamaarGJS02, § 4]). The universal property of
$(T^{*}K)_{\mathrm {impl}}$ (see [Reference Guillemin, Jeffrey and SjamaarGJS02, § 4]). The universal property of ![]() $(T^{*}K)_{\mathrm {impl}}$ (see [Reference Guillemin, Jeffrey and SjamaarGJS02, Theorem 4.9]) is then a special case of Theorem 4.11.
$(T^{*}K)_{\mathrm {impl}}$ (see [Reference Guillemin, Jeffrey and SjamaarGJS02, Theorem 4.9]) is then a special case of Theorem 4.11.
4.8 Symplectic cutting
The following subsection only applies to the smooth category.
The symplectic cut construction of Lerman [Reference LermanLer95] and its generalization to torus actions [Reference Lerman, Meinrenken, Tolman and WoodwardLMTW98] can be viewed as symplectic reduction along a polyhedral set, as we now explain.
Let ![]() $(M, \omega )$ be a symplectic manifold with an effective action of a compact torus
$(M, \omega )$ be a symplectic manifold with an effective action of a compact torus ![]() $T$ with moment map
$T$ with moment map ![]() $\mu : M \longrightarrow \mathfrak {t}^{*}$. Following [Reference Lerman, Meinrenken, Tolman and WoodwardLMTW98, § 2], let
$\mu : M \longrightarrow \mathfrak {t}^{*}$. Following [Reference Lerman, Meinrenken, Tolman and WoodwardLMTW98, § 2], let ![]() $P \subseteq \mathfrak {t}^{*}$ be a convex rational polyhedral set of the form
$P \subseteq \mathfrak {t}^{*}$ be a convex rational polyhedral set of the form
for some ![]() $N \in \mathbb {N}$,
$N \in \mathbb {N}$, ![]() $v_1, \ldots, v_N \in \mathfrak {t}$ in the integral lattice of
$v_1, \ldots, v_N \in \mathfrak {t}$ in the integral lattice of ![]() $T$, and
$T$, and ![]() $b=(b_1,\ldots,b_N) \in \mathbb {R}^{N}$. The vectors
$b=(b_1,\ldots,b_N) \in \mathbb {R}^{N}$. The vectors ![]() $v_i$ define a Hamiltonian action of
$v_i$ define a Hamiltonian action of ![]() $(S^{1})^{N}$ on
$(S^{1})^{N}$ on ![]() $M \times \mathbb {C}^{N}$ with moment map
$M \times \mathbb {C}^{N}$ with moment map ![]() $\nu : M \times \mathbb {C}^{N} \longrightarrow \mathbb {R}^{N}$, where the
$\nu : M \times \mathbb {C}^{N} \longrightarrow \mathbb {R}^{N}$, where the ![]() $i$th component of
$i$th component of ![]() $\nu$ is
$\nu$ is ![]() $\nu _i(p, z) = \mu (p)(v_i) - |z_i|^{2}$. The symplectic cut of
$\nu _i(p, z) = \mu (p)(v_i) - |z_i|^{2}$. The symplectic cut of ![]() $M$ with respect to
$M$ with respect to ![]() $P$ is the Marsden–Weinstein–Meyer reduction of
$P$ is the Marsden–Weinstein–Meyer reduction of ![]() $M \times \mathbb {C}^{N}$ by
$M \times \mathbb {C}^{N}$ by ![]() $(S^{1})^{N}$ at level
$(S^{1})^{N}$ at level ![]() $b$. We denote this reduced space by
$b$. We denote this reduced space by ![]() $M_P$.
$M_P$.
Although ![]() $M_P$ is singular in general, it is stratified into symplectic manifolds. A more precise statement is that
$M_P$ is singular in general, it is stratified into symplectic manifolds. A more precise statement is that
where the union ranges over the open faces ![]() $F$ of
$F$ of ![]() $P$ and
$P$ and ![]() $T_F \subseteq T$ is the torus whose Lie algebra is
$T_F \subseteq T$ is the torus whose Lie algebra is ![]() $(T_\xi F)^{\circ } \subseteq \mathfrak {t}$ for any
$(T_\xi F)^{\circ } \subseteq \mathfrak {t}$ for any ![]() $\xi \in F$. Each manifold
$\xi \in F$. Each manifold ![]() $\mu ^{-1}(F) / T_F$ is given a symplectic structure
$\mu ^{-1}(F) / T_F$ is given a symplectic structure ![]() $\omega _F$ characterized by
$\omega _F$ characterized by
where ![]() $\pi _F : \mu ^{-1}(F) \longrightarrow \mu ^{-1}(F) / T_F$ is the quotient map and
$\pi _F : \mu ^{-1}(F) \longrightarrow \mu ^{-1}(F) / T_F$ is the quotient map and ![]() $i_F : \mu ^{-1}(F) \longrightarrow M$ the inclusion map.
$i_F : \mu ^{-1}(F) \longrightarrow M$ the inclusion map.
As the Poisson structure on ![]() $\mathfrak {t}^{*}$ is trivial, every face
$\mathfrak {t}^{*}$ is trivial, every face ![]() $F$ is Poisson and, hence, stable (Lemma 4.14). Theorem 4.17(ii) then shows that
$F$ is Poisson and, hence, stable (Lemma 4.14). Theorem 4.17(ii) then shows that ![]() $T_F \times F$ is a source-connected stabilizer subgroupoid of
$T_F \times F$ is a source-connected stabilizer subgroupoid of ![]() $F$ in
$F$ in ![]() $T^{*}T$. The symplectic manifold
$T^{*}T$. The symplectic manifold ![]() $\mu ^{-1}(F) / T_F$ is then the symplectic reduction
$\mu ^{-1}(F) / T_F$ is then the symplectic reduction ![]() $M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{F}} T$ of
$M \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{F}} T$ of ![]() $M$ by
$M$ by ![]() $T$ along
$T$ along ![]() $F$. These considerations allow us to deduce the following result.
$F$. These considerations allow us to deduce the following result.
Proposition 4.32 (Theorem F(iii))
The symplectic reduction of ![]() $M$ by
$M$ by ![]() $T$ along a polyhedral set
$T$ along a polyhedral set ![]() $P$ is the symplectic cut of
$P$ is the symplectic cut of ![]() $M$ with respect to
$M$ with respect to ![]() $P$, i.e.
$P$, i.e.
4.9 Symplectic reduction along a decomposition class
Let ![]() $G$ be a connected complex semisimple linear algebraic group with Lie algebra
$G$ be a connected complex semisimple linear algebraic group with Lie algebra ![]() $\mathfrak {g}$, and let
$\mathfrak {g}$, and let ![]() $\mathfrak {g}_x$ denote the
$\mathfrak {g}_x$ denote the ![]() $\mathfrak {g}$-centralizer of
$\mathfrak {g}$-centralizer of ![]() $x\in \mathfrak {g}$. Write
$x\in \mathfrak {g}$. Write ![]() $x=x_s+x_n$ for the Jordan decomposition of any
$x=x_s+x_n$ for the Jordan decomposition of any ![]() $x\in \mathfrak {g}$ into a semisimple element
$x\in \mathfrak {g}$ into a semisimple element ![]() $x_s\in \mathfrak {g}$ and a nilpotent element
$x_s\in \mathfrak {g}$ and a nilpotent element ![]() $x_n\in \mathfrak {g}$. This gives rise to an equivalence relation
$x_n\in \mathfrak {g}$. This gives rise to an equivalence relation ![]() $\sim$ on
$\sim$ on ![]() $\mathfrak {g}$, in which
$\mathfrak {g}$, in which ![]() $x\sim y$ if and only if
$x\sim y$ if and only if ![]() $\mathfrak {g}_{x_s}=\mathrm {Ad}_g(\mathfrak {g}_{y_s})$ and
$\mathfrak {g}_{x_s}=\mathrm {Ad}_g(\mathfrak {g}_{y_s})$ and ![]() $x_n=\mathrm {Ad}_g y_n$ for some
$x_n=\mathrm {Ad}_g y_n$ for some ![]() $g\in G$. The resulting equivalence classes are called decomposition classes (also known as Jordan classes) and play an important role in Lie-theoretic geometry [Reference Borho and KraftBK79, Reference BroerBro98a, Reference BroerBro98b, Reference SpaltensteinSpa82, Reference Im HofImH05, Reference MoreauMor08, Reference PopovPop08]. Among other things, each decomposition class
$g\in G$. The resulting equivalence classes are called decomposition classes (also known as Jordan classes) and play an important role in Lie-theoretic geometry [Reference Borho and KraftBK79, Reference BroerBro98a, Reference BroerBro98b, Reference SpaltensteinSpa82, Reference Im HofImH05, Reference MoreauMor08, Reference PopovPop08]. Among other things, each decomposition class ![]() $\mathcal {D}\subseteq \mathfrak {g}$ is a smooth [Reference BroerBro98b, Corollary 3.8.1(i)], locally closed [Reference Tauvel and YuTY05, Corollary 39.1.7(ii)],
$\mathcal {D}\subseteq \mathfrak {g}$ is a smooth [Reference BroerBro98b, Corollary 3.8.1(i)], locally closed [Reference Tauvel and YuTY05, Corollary 39.1.7(ii)], ![]() $G$-invariant subvariety of
$G$-invariant subvariety of ![]() $\mathfrak {g}$. It follows from Lemma 4.16 that
$\mathfrak {g}$. It follows from Lemma 4.16 that ![]() $\mathcal {D}$ is a stable subvariety of
$\mathcal {D}$ is a stable subvariety of ![]() $\mathfrak {g}$, allowing us to concretely study stabilizer subgroupoids of
$\mathfrak {g}$, allowing us to concretely study stabilizer subgroupoids of ![]() $\mathcal {D}$ in the cotangent groupoid
$\mathcal {D}$ in the cotangent groupoid ![]() $T^{*}G\rightrightarrows \mathfrak {g}$. On the other hand, suppose that
$T^{*}G\rightrightarrows \mathfrak {g}$. On the other hand, suppose that ![]() $x\in \mathcal {D}$ and consider the
$x\in \mathcal {D}$ and consider the ![]() $[G_{x_s},G_{x_s}]$-stabilizer
$[G_{x_s},G_{x_s}]$-stabilizer ![]() $[G_{x_s},G_{x_s}]_{x_n}$ and
$[G_{x_s},G_{x_s}]_{x_n}$ and ![]() $[\mathfrak {g}_{x_s},\mathfrak {g}_{x_s}]$-centralizer
$[\mathfrak {g}_{x_s},\mathfrak {g}_{x_s}]$-centralizer ![]() $[\mathfrak {g}_{x_s},\mathfrak {g}_{x_s}]_{x_n}$ of the nilpotent part
$[\mathfrak {g}_{x_s},\mathfrak {g}_{x_s}]_{x_n}$ of the nilpotent part ![]() $x_n\in [\mathfrak {g}_{x_s},\mathfrak {g}_{x_s}]$. Let us also consider the identity component
$x_n\in [\mathfrak {g}_{x_s},\mathfrak {g}_{x_s}]$. Let us also consider the identity component ![]() $[G_{x_s},G_{x_s}]_{x_n}^{\circ }$ of
$[G_{x_s},G_{x_s}]_{x_n}^{\circ }$ of ![]() $[G_{x_s},G_{x_s}]_{x_n}$ for each
$[G_{x_s},G_{x_s}]_{x_n}$ for each ![]() $x\in \mathcal {D}$. The group scheme
$x\in \mathcal {D}$. The group scheme
is a subgroupoid of ![]() $T^{*}G\rightrightarrows \mathfrak {g}$ if we use the Killing form and left trivialization to identity
$T^{*}G\rightrightarrows \mathfrak {g}$ if we use the Killing form and left trivialization to identity ![]() $T^{*}G$ with
$T^{*}G$ with ![]() $G\times \mathfrak {g}$.
$G\times \mathfrak {g}$.
Remark 4.33 The conjugacy classes of ![]() $[G_{x_s},G_{x_s}]_{x_n}$ in
$[G_{x_s},G_{x_s}]_{x_n}$ in ![]() $G$ and
$G$ and ![]() $[\mathfrak {g}_{x_s},\mathfrak {g}_{x_s}]_{x_n}$ in
$[\mathfrak {g}_{x_s},\mathfrak {g}_{x_s}]_{x_n}$ in ![]() $\mathfrak {g}$ are easily seen to be independent of
$\mathfrak {g}$ are easily seen to be independent of ![]() $x\in \mathcal {D}$. It follows that any two fibers of (4.15) are isomorphic as algebraic groups.
$x\in \mathcal {D}$. It follows that any two fibers of (4.15) are isomorphic as algebraic groups.
Remark 4.34 If ![]() $x\in \mathfrak {g}$ is semisimple, then
$x\in \mathfrak {g}$ is semisimple, then ![]() $[G_{x_s},G_{x_s}]_{x_n}^{\circ }=[G_x,G_x]$. The stabilizer subgroupoid (4.15) thereby takes a simpler form if
$[G_{x_s},G_{x_s}]_{x_n}^{\circ }=[G_x,G_x]$. The stabilizer subgroupoid (4.15) thereby takes a simpler form if ![]() $\mathcal {D}$ consists of semisimple elements.
$\mathcal {D}$ consists of semisimple elements.
Proposition 4.35 If ![]() $\mathcal {D}\subseteq \mathfrak {g}$ is a decomposition class, then
$\mathcal {D}\subseteq \mathfrak {g}$ is a decomposition class, then ![]() $\pi :\mathcal {H}\longrightarrow \mathcal {D}$ is a stabilizer subgroupoid of
$\pi :\mathcal {H}\longrightarrow \mathcal {D}$ is a stabilizer subgroupoid of ![]() $\mathcal {D}$ in
$\mathcal {D}$ in ![]() $T^{*}G\rightrightarrows \mathfrak {g}$. Furthermore,
$T^{*}G\rightrightarrows \mathfrak {g}$. Furthermore, ![]() $(\mathcal {D},\mathcal {H})$ is a clean reduction datum for the action of
$(\mathcal {D},\mathcal {H})$ is a clean reduction datum for the action of ![]() $G$ on
$G$ on ![]() $T^{*}G$ by right translations.
$T^{*}G$ by right translations.
Proof. We begin by verifying that ![]() $\mathcal {H}$ is closed in
$\mathcal {H}$ is closed in ![]() $G\times \mathcal {D}$. To this end, fix any
$G\times \mathcal {D}$. To this end, fix any ![]() $y\in \mathcal {D}$, set
$y\in \mathcal {D}$, set ![]() $Q:= [G_{y_s},G_{y_s}]_{y_n}^{\circ }$, and let
$Q:= [G_{y_s},G_{y_s}]_{y_n}^{\circ }$, and let ![]() $R$ be the normalizer of
$R$ be the normalizer of ![]() $Q$ in
$Q$ in ![]() $G$. We may
$G$. We may ![]() $G$-equivariantly identify
$G$-equivariantly identify ![]() $G/R$ with the set of closed subgroups in
$G/R$ with the set of closed subgroups in ![]() $G$ conjugate to
$G$ conjugate to ![]() $Q$, i.e. via the unique
$Q$, i.e. via the unique ![]() $G$-equivariant bijection sending the identity coset
$G$-equivariant bijection sending the identity coset ![]() $[1]\in G/R$ to
$[1]\in G/R$ to ![]() $Q$. Associating the subgroup
$Q$. Associating the subgroup ![]() $[G_{x_s},G_{x_s}]_{x_n}^{\circ }$ to each
$[G_{x_s},G_{x_s}]_{x_n}^{\circ }$ to each ![]() $x\in \mathcal {D}$ then defines a continuous map
$x\in \mathcal {D}$ then defines a continuous map ![]() $\phi :\mathcal {D}\longrightarrow G/R$. On the other hand, we may choose an open neighborhood
$\phi :\mathcal {D}\longrightarrow G/R$. On the other hand, we may choose an open neighborhood ![]() $U\subseteq G/R$ of
$U\subseteq G/R$ of ![]() $[1]$ and a holomorphic section
$[1]$ and a holomorphic section ![]() $s:U\longrightarrow G$ of
$s:U\longrightarrow G$ of ![]() $G\longrightarrow G/R$ satisfying
$G\longrightarrow G/R$ satisfying ![]() $s([1])=1$. Now set
$s([1])=1$. Now set ![]() $V:= \phi ^{-1}(U)\subseteq \mathcal {D}$ and note that
$V:= \phi ^{-1}(U)\subseteq \mathcal {D}$ and note that
is a holomorphic map satisfying
for all ![]() $x\in V$. The map
$x\in V$. The map
then defines a trivialization of ![]() $\pi :\mathcal {H}\longrightarrow \mathcal {D}$ over
$\pi :\mathcal {H}\longrightarrow \mathcal {D}$ over ![]() $V$. As
$V$. As ![]() $Q$ is closed in
$Q$ is closed in ![]() $G$, we conclude that
$G$, we conclude that ![]() $\mathcal {H}$ is closed in
$\mathcal {H}$ is closed in ![]() $G\times \mathcal {D}$.
$G\times \mathcal {D}$.
We now note that
where
is the locus of elements in ![]() $\mathfrak {z}(\mathfrak {g}_{x_s})$ having
$\mathfrak {z}(\mathfrak {g}_{x_s})$ having ![]() $\mathfrak {g}$-centralizers of minimal dimension [Reference Tauvel and YuTY05, Corollary 39.1.7]. This description of
$\mathfrak {g}$-centralizers of minimal dimension [Reference Tauvel and YuTY05, Corollary 39.1.7]. This description of ![]() $\mathcal {D}$ implies that
$\mathcal {D}$ implies that
for all ![]() $x\in \mathcal {D}$. Writing
$x\in \mathcal {D}$. Writing ![]() $V^{\perp }\subseteq \mathfrak {g}$ for the annihilator of any subspace
$V^{\perp }\subseteq \mathfrak {g}$ for the annihilator of any subspace ![]() $V\subseteq \mathfrak {g}$ under the Killing form, we conclude that
$V\subseteq \mathfrak {g}$ under the Killing form, we conclude that
 \begin{align*} (T_x\mathcal{D})^{\perp} & = \mathfrak{z}(\mathfrak{g}_{x_s})^{\perp}\cap[\mathfrak{g},x]^{\perp}\\ & = \mathfrak{z}(\mathfrak{g}_{x_s})^{\perp} \cap\mathfrak{g}_x\\ & = (\mathfrak{z}(\mathfrak{g}_{x_s})^{\perp}\cap\mathfrak{g}_{x_s})\cap\mathfrak{g}_{x_n}\\ & = [\mathfrak{g}_{x_s},\mathfrak{g}_{x_s}]\cap\mathfrak{g}_{x_n}\\ & = [\mathfrak{g}_{x_s},\mathfrak{g}_{x_s}]_{x_n} \end{align*}
\begin{align*} (T_x\mathcal{D})^{\perp} & = \mathfrak{z}(\mathfrak{g}_{x_s})^{\perp}\cap[\mathfrak{g},x]^{\perp}\\ & = \mathfrak{z}(\mathfrak{g}_{x_s})^{\perp} \cap\mathfrak{g}_x\\ & = (\mathfrak{z}(\mathfrak{g}_{x_s})^{\perp}\cap\mathfrak{g}_{x_s})\cap\mathfrak{g}_{x_n}\\ & = [\mathfrak{g}_{x_s},\mathfrak{g}_{x_s}]\cap\mathfrak{g}_{x_n}\\ & = [\mathfrak{g}_{x_s},\mathfrak{g}_{x_s}]_{x_n} \end{align*}
for all ![]() $x\in \mathcal {D}$. This combines with the source-connectedness of
$x\in \mathcal {D}$. This combines with the source-connectedness of ![]() $\mathcal {H}\longrightarrow \mathcal {D}$, the closedness of
$\mathcal {H}\longrightarrow \mathcal {D}$, the closedness of ![]() $\mathcal {H}$ in
$\mathcal {H}$ in ![]() $G\times \mathcal {D}$, and Theorem 4.17 to imply that
$G\times \mathcal {D}$, and Theorem 4.17 to imply that ![]() $\mathcal {H}$ is a stabilizer subgroupoid of
$\mathcal {H}$ is a stabilizer subgroupoid of ![]() $\mathcal {D}$ in
$\mathcal {D}$ in ![]() $T^{*}G\rightrightarrows \mathfrak {g}^{*}$.
$T^{*}G\rightrightarrows \mathfrak {g}^{*}$.
It remains only to prove that ![]() $(\mathcal {D},\mathcal {H})$ is a clean reduction datum. However, this is an immediate consequence of Proposition 4.10(ii).
$(\mathcal {D},\mathcal {H})$ is a clean reduction datum. However, this is an immediate consequence of Proposition 4.10(ii).
The clean reduction datum ![]() $(\mathcal {D},\mathcal {H})$ in Proposition 4.35 determines a universal reduced space
$(\mathcal {D},\mathcal {H})$ in Proposition 4.35 determines a universal reduced space ![]() $\mathfrak {M}_{G,\mathcal {D},\mathcal {H}}=\mathfrak {M}_{G,\mathcal {D}}$. An examination of (4.15) reveals that
$\mathfrak {M}_{G,\mathcal {D},\mathcal {H}}=\mathfrak {M}_{G,\mathcal {D}}$. An examination of (4.15) reveals that
where ![]() $G$ acts on the third space via left multiplication on each factor. Given any
$G$ acts on the third space via left multiplication on each factor. Given any ![]() $x\in \mathcal {D}$, this observation and the proof of Proposition 4.35 allow us to describe the tangent space of
$x\in \mathcal {D}$, this observation and the proof of Proposition 4.35 allow us to describe the tangent space of ![]() $([1],x)\in \mathfrak {M}_{G,\mathcal {D}}$ as
$([1],x)\in \mathfrak {M}_{G,\mathcal {D}}$ as
One immediate consequence is that
for all ![]() $x\in \mathcal {D}$. Another consequence is that the symplectic form
$x\in \mathcal {D}$. Another consequence is that the symplectic form ![]() $\omega$ on
$\omega$ on ![]() $\mathfrak {M}_{G,\mathcal {D}}$ is characterized by being
$\mathfrak {M}_{G,\mathcal {D}}$ is characterized by being ![]() $G$-invariant and defined as follows on
$G$-invariant and defined as follows on ![]() $T_{(x,[1])}\mathfrak {M}_{G,\mathcal {D}}=\mathfrak {g}/[\mathfrak {g}_{x_s},\mathfrak {g}_{x_s}]_{x_n}\oplus [\mathfrak {g}_{x_s},\mathfrak {g}_{x_s}]_{x_n}^{\perp }$ for all
$T_{(x,[1])}\mathfrak {M}_{G,\mathcal {D}}=\mathfrak {g}/[\mathfrak {g}_{x_s},\mathfrak {g}_{x_s}]_{x_n}\oplus [\mathfrak {g}_{x_s},\mathfrak {g}_{x_s}]_{x_n}^{\perp }$ for all ![]() $x\in \mathcal {D}$:
$x\in \mathcal {D}$:
for all ![]() $[u_1],[u_2]\in \mathfrak {g}/[\mathfrak {g}_{x_s},\mathfrak {g}_{x_s}]_{x_n}$ and
$[u_1],[u_2]\in \mathfrak {g}/[\mathfrak {g}_{x_s},\mathfrak {g}_{x_s}]_{x_n}$ and ![]() $\zeta _1,\zeta _2\in [\mathfrak {g}_{x_s},\mathfrak {g}_{x_s}]_{x_n}^{\perp }$, where
$\zeta _1,\zeta _2\in [\mathfrak {g}_{x_s},\mathfrak {g}_{x_s}]_{x_n}^{\perp }$, where ![]() $\langle {\cdot }\,{,}\,{\cdot }\rangle$ denotes the Killing form on
$\langle {\cdot }\,{,}\,{\cdot }\rangle$ denotes the Killing form on ![]() $\mathfrak {g}$; this formula is a consequence of (4.1) and Theorem 3.10(iv). We also know that
$\mathfrak {g}$; this formula is a consequence of (4.1) and Theorem 3.10(iv). We also know that ![]() $\mathfrak {M}_{G,\mathcal {D}}$ has the structure of a holomorphic symplectic groupoid integrating
$\mathfrak {M}_{G,\mathcal {D}}$ has the structure of a holomorphic symplectic groupoid integrating ![]() $\mathcal {D}$, as follows from Theorem 4.21 and Proposition 4.35.
$\mathcal {D}$, as follows from Theorem 4.21 and Proposition 4.35.
Example 4.36 (Theorem E(ii))
We now discuss a curious application of this discussion. Consider the subsets
of irregular, semisimple, and subregular elements in ![]() $\mathfrak {g}$, respectively. The intersection
$\mathfrak {g}$, respectively. The intersection
is an open dense subset of ![]() $\mathfrak {g}_{\text {irr}}$ equal to the disjoint union of finitely many decomposition classes [Reference PopovPop08, Remark 3.7(a)]. Each of these decomposition classes consists of semisimple elements and has codimension three in
$\mathfrak {g}_{\text {irr}}$ equal to the disjoint union of finitely many decomposition classes [Reference PopovPop08, Remark 3.7(a)]. Each of these decomposition classes consists of semisimple elements and has codimension three in ![]() $\mathfrak {g}$ (see [Reference PopovPop08, Lemma 3.6]). These considerations and Proposition 4.35 imply that
$\mathfrak {g}$ (see [Reference PopovPop08, Lemma 3.6]). These considerations and Proposition 4.35 imply that ![]() $\mathfrak {g}_{\text {irr}}^{\circ }\subseteq \mathfrak {g}$ is a smooth,
$\mathfrak {g}_{\text {irr}}^{\circ }\subseteq \mathfrak {g}$ is a smooth, ![]() $G$-invariant, stable subvariety of
$G$-invariant, stable subvariety of ![]() $\mathfrak {g}$ admitting
$\mathfrak {g}$ admitting
as a source-connected stabilizer subgroupoid. It follows that
where ![]() $G$ acts on the right-hand side by left multiplication on each factor. Each of the subgroups
$G$ acts on the right-hand side by left multiplication on each factor. Each of the subgroups ![]() $[G_x,G_x]$ appearing above is three-dimensional and has Lie algebra
$[G_x,G_x]$ appearing above is three-dimensional and has Lie algebra ![]() $[\mathfrak {g}_x,\mathfrak {g}_x]\cong \mathfrak {sl}_2$. This combines with (4.16) to yield
$[\mathfrak {g}_x,\mathfrak {g}_x]\cong \mathfrak {sl}_2$. This combines with (4.16) to yield
The symplectic form and symplectic groupoid structure on ![]() $\mathfrak {M}_{G,\mathfrak {g}_{\text {irr}}^{\circ }}$ are described analogously to those on
$\mathfrak {M}_{G,\mathfrak {g}_{\text {irr}}^{\circ }}$ are described analogously to those on ![]() $\mathfrak {M}_{G,\mathcal {D}}$ in the previous paragraph.
$\mathfrak {M}_{G,\mathcal {D}}$ in the previous paragraph.
5. Main construction: algebraic version
We now develop, prove, and explore the consequences of Theorem C, a counterpart of Theorems A and B in complex algebraic geometry. This undertaking begins with some algebro-geometric preliminaries in § 5.1. Theorem C is proved in § 5.2 and followed by examples in § 5.3 and § 5.4. The last of these sections uses Theorem C to derive the Ginzburg–Kazhdan construction of Moore–Tachikawa varieties.
5.1 Algebro-geometric preliminaries
In the interest of clarity, we now briefly outline the algebro-geometric counterparts of some definitions in § 3. We work exclusively with algebraic varieties over ![]() $\mathbb {C}$.
$\mathbb {C}$.
5.1.1 Quotients
Suppose that an algebraic groupoid ![]() $\mathcal {H} \rightrightarrows S$ acts algebraically on a variety
$\mathcal {H} \rightrightarrows S$ acts algebraically on a variety ![]() $N$. An
$N$. An ![]() $\mathcal {H}$-invariant variety morphism
$\mathcal {H}$-invariant variety morphism ![]() $\pi :N \longrightarrow Q$ then determines a sheaf
$\pi :N \longrightarrow Q$ then determines a sheaf ![]() $(\pi _*\mathcal {O}_N)^{\mathcal {H}}$ on
$(\pi _*\mathcal {O}_N)^{\mathcal {H}}$ on ![]() $Q$, i.e.
$Q$, i.e. ![]() $(\pi _*\mathcal {O}_N)^{\mathcal {H}}(U)$ is the algebra of
$(\pi _*\mathcal {O}_N)^{\mathcal {H}}(U)$ is the algebra of ![]() $\mathcal {H}$-invariant elements of
$\mathcal {H}$-invariant elements of ![]() $\mathcal {O}_N(\pi ^{-1}(U))$ for each open subset
$\mathcal {O}_N(\pi ^{-1}(U))$ for each open subset ![]() $U \subseteq Q$. Observe that pulling back along
$U \subseteq Q$. Observe that pulling back along ![]() $\pi$ defines a sheaf morphism
$\pi$ defines a sheaf morphism
Definition 5.1 Suppose that an algebraic groupoid ![]() $\mathcal {H}\rightrightarrows S$ acts algebraically on an algebraic variety
$\mathcal {H}\rightrightarrows S$ acts algebraically on an algebraic variety ![]() $N$. We define an algebraic quotient of
$N$. We define an algebraic quotient of ![]() $N$ by
$N$ by ![]() $\mathcal {H}$ to be an
$\mathcal {H}$ to be an ![]() $\mathcal {H}$-invariant morphism
$\mathcal {H}$-invariant morphism ![]() $\pi :N\longrightarrow Q$ for which (5.1) is an isomorphism.
$\pi :N\longrightarrow Q$ for which (5.1) is an isomorphism.
Example 5.2 If ![]() $N$ is an affine variety and the algebra
$N$ is an affine variety and the algebra ![]() $\mathbb {C}[N]^{\mathbb {\mathcal {H}}}$ of
$\mathbb {C}[N]^{\mathbb {\mathcal {H}}}$ of ![]() $\mathcal {H}$-invariant regular functions is finitely generated, then the morphism
$\mathcal {H}$-invariant regular functions is finitely generated, then the morphism ![]() $N \longrightarrow \operatorname {Spec}\mathbb {C}[N]^{\mathcal {\mathcal {H}}}$ is an algebraic quotient.
$N \longrightarrow \operatorname {Spec}\mathbb {C}[N]^{\mathcal {\mathcal {H}}}$ is an algebraic quotient.
5.1.2 Stabilizer subgroupoids
We shall use the term symplectic variety in reference to a smooth algebraic variety endowed with an algebraic symplectic form. The term Poisson variety shall be used for a potentially singular algebraic variety ![]() $X$ whose structure sheaf
$X$ whose structure sheaf ![]() $\mathcal {O}_X$ is a sheaf of Poisson algebras. Now suppose that
$\mathcal {O}_X$ is a sheaf of Poisson algebras. Now suppose that ![]() $X$ is a smooth Poisson variety. The Poisson bracket can then be encoded by a Poisson bivector field
$X$ is a smooth Poisson variety. The Poisson bracket can then be encoded by a Poisson bivector field ![]() $\sigma :T^{*}X\longrightarrow TX$. A smooth locally-closed subvariety
$\sigma :T^{*}X\longrightarrow TX$. A smooth locally-closed subvariety ![]() $S\subseteq X$ shall be called pre-Poisson if
$S\subseteq X$ shall be called pre-Poisson if ![]() $\sigma ^{-1}(TS) \cap TS^{\circ }$ has constant rank over
$\sigma ^{-1}(TS) \cap TS^{\circ }$ has constant rank over ![]() $S$.
$S$.
Now let ![]() $\mathcal {G}\rightrightarrows X$ be an algebraic groupoid for which
$\mathcal {G}\rightrightarrows X$ be an algebraic groupoid for which ![]() $\mathcal {G}$ and
$\mathcal {G}$ and ![]() $X$ are smooth varieties. If
$X$ are smooth varieties. If ![]() $\mathcal {G}$ comes equipped with an algebraic symplectic form
$\mathcal {G}$ comes equipped with an algebraic symplectic form ![]() $\Omega$ such that the graph of multiplication is Lagrangian in
$\Omega$ such that the graph of multiplication is Lagrangian in ![]() $\mathcal {G} \times \mathcal {G} \times \mathcal {G}^{-}$, then
$\mathcal {G} \times \mathcal {G} \times \mathcal {G}^{-}$, then ![]() $\mathcal {G}\rightrightarrows X$ shall be called an algebraic symplectic groupoid. Each pre-Poisson subvariety
$\mathcal {G}\rightrightarrows X$ shall be called an algebraic symplectic groupoid. Each pre-Poisson subvariety ![]() $S\subseteq X$ then determines a Lie subalgebroid
$S\subseteq X$ then determines a Lie subalgebroid
of ![]() $T^{*}X\cong \mathrm {Lie}(\mathcal {G})$, to be called the stabilizer subalgebroid of
$T^{*}X\cong \mathrm {Lie}(\mathcal {G})$, to be called the stabilizer subalgebroid of ![]() $S$. We define a stabilizer subgroupoid of
$S$. We define a stabilizer subgroupoid of ![]() $S$ in
$S$ in ![]() $\mathcal {G}$ to be any smooth algebraic groupoid
$\mathcal {G}$ to be any smooth algebraic groupoid ![]() $\mathcal {H}\rightrightarrows S$ integrating
$\mathcal {H}\rightrightarrows S$ integrating ![]() $L_S$, together with an algebraic Lie groupoid homomorphism
$L_S$, together with an algebraic Lie groupoid homomorphism ![]() $j : \mathcal {H} \longrightarrow \mathcal {G}$ such that
$j : \mathcal {H} \longrightarrow \mathcal {G}$ such that ![]() $j^{*}\Omega = 0$.
$j^{*}\Omega = 0$.
5.1.3 Algebraic Hamiltonian systems
Definition 2.1 has an obvious algebro-geometric analog, i.e. a notion of an algebraic Hamiltonian action of an algebraic symplectic groupoid on a symplectic variety. In turn, this gives rise to the definition of an algebraic Hamiltonian system.
5.2 Complex algebraic symplectic reduction along a subvariety
Given any algebraic variety ![]() $(Z,\mathcal {O}_Z)$, let
$(Z,\mathcal {O}_Z)$, let ![]() $\mathcal {O}^{\text {an}}_Z$ denote the structure sheaf that realizes
$\mathcal {O}^{\text {an}}_Z$ denote the structure sheaf that realizes ![]() $Z$ as a complex analytic space. For a point
$Z$ as a complex analytic space. For a point ![]() $z \in Z$, we may identify the stalk
$z \in Z$, we may identify the stalk ![]() $\mathcal {O}_{Z,z}$ with a subalgebra of
$\mathcal {O}_{Z,z}$ with a subalgebra of ![]() $\mathcal {O}_{Z, z}^{\text {an}}$.
$\mathcal {O}_{Z, z}^{\text {an}}$.
Theorem 5.3 (Theorem C)
Let ![]() $((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$ be an algebraic Hamiltonian system and
$((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$ be an algebraic Hamiltonian system and ![]() $S\subseteq X$ a pre-Poisson subvariety for which
$S\subseteq X$ a pre-Poisson subvariety for which ![]() $N:= \mu ^{-1}(S)$ is reduced. Suppose that
$N:= \mu ^{-1}(S)$ is reduced. Suppose that ![]() $\pi : N \longrightarrow Q$ is an algebraic quotient of
$\pi : N \longrightarrow Q$ is an algebraic quotient of ![]() $N$ by a stabilizer subgroupoid
$N$ by a stabilizer subgroupoid ![]() $\mathcal {H}\rightrightarrows S$ of
$\mathcal {H}\rightrightarrows S$ of ![]() $S$.
$S$.
(i) For all
 $p \in N$ and
$p \in N$ and  $f \in \mathcal {O}_{Q, \pi (p)}$, there exists
$f \in \mathcal {O}_{Q, \pi (p)}$, there exists  $F \in \mathcal {O}_{M, p}^{\mathrm {an}}$ such that
$F \in \mathcal {O}_{M, p}^{\mathrm {an}}$ such that  $\pi ^{*}f = F\vert _N \in \mathcal {O}_{N, p}^{\mathrm {an}}$ and
$\pi ^{*}f = F\vert _N \in \mathcal {O}_{N, p}^{\mathrm {an}}$ and  $dF(TN^{\omega }) = 0$.
$dF(TN^{\omega }) = 0$.(ii) There is a unique algebraic Poisson structure
 $\{{\cdot }\,{,}\,{\cdot }\}_Q$ on
$\{{\cdot }\,{,}\,{\cdot }\}_Q$ on  $Q$ such that
for all
$Q$ such that
for all \begin{align*} \pi^{*}\{f, g\}_Q = \{F, G\}\vert_N \end{align*}
\begin{align*} \pi^{*}\{f, g\}_Q = \{F, G\}\vert_N \end{align*} $f, g \in \mathcal {O}_{Q, \pi (p)}$ and
$f, g \in \mathcal {O}_{Q, \pi (p)}$ and  $F, G \in \mathcal {O}_{M, p}^{\mathrm {an}}$ related to
$F, G \in \mathcal {O}_{M, p}^{\mathrm {an}}$ related to  $f, g$ as in part (i).
$f, g$ as in part (i).(iii) Assume that there exists
 $p \in N$ such that
$p \in N$ such that  $d\pi _p$ is surjective,
$d\pi _p$ is surjective,  $\pi ^{-1}(\pi (p))$ is an
$\pi ^{-1}(\pi (p))$ is an  $\mathcal {H}$-orbit, and
$\mathcal {H}$-orbit, and  $\pi (p)$ is a smooth point of
$\pi (p)$ is a smooth point of  $Q$. The Poisson structure in part (ii) is then non-degenerate on a Zariski-open subset of the smooth locus of
$Q$. The Poisson structure in part (ii) is then non-degenerate on a Zariski-open subset of the smooth locus of  $Q$ containing
$Q$ containing  $\pi (p)$.
$\pi (p)$.
Proof. To prove part (i), let ![]() $D := TN \cap TN^{\omega }$. By Proposition 3.7, we have
$D := TN \cap TN^{\omega }$. By Proposition 3.7, we have ![]() $D_q = T_q(\mathcal {H} \cdot q)$ for all
$D_q = T_q(\mathcal {H} \cdot q)$ for all ![]() $q \in N$. It follows that
$q \in N$. It follows that
and ![]() $d(\pi ^{*}f)(D) = 0$, so we can find such an
$d(\pi ^{*}f)(D) = 0$, so we can find such an ![]() $F$ by Proposition 3.6.
$F$ by Proposition 3.6.
To prove part (ii), let ![]() $U \subseteq Q$ be Zariski-open. Theorem 3.8 provides a Poisson bracket
$U \subseteq Q$ be Zariski-open. Theorem 3.8 provides a Poisson bracket ![]() $\{{\cdot }\,{,}\,{\cdot }\}'$ on
$\{{\cdot }\,{,}\,{\cdot }\}'$ on ![]() $\mathcal {O}_N^{\mathrm {an}}(\pi ^{-1}(U))^{\mathcal{H}}$. It suffices to show that the subalgebra
$\mathcal {O}_N^{\mathrm {an}}(\pi ^{-1}(U))^{\mathcal{H}}$. It suffices to show that the subalgebra ![]() $\mathcal {O}_N(\pi ^{-1}(U))^{\mathcal{H}} \cong \mathcal {O}_Q(U)$ of algebraic functions is closed under this bracket.
$\mathcal {O}_N(\pi ^{-1}(U))^{\mathcal{H}} \cong \mathcal {O}_Q(U)$ of algebraic functions is closed under this bracket.
Let ![]() $f, g \in \mathcal {O}_Q(U)$, let
$f, g \in \mathcal {O}_Q(U)$, let ![]() $p \in \pi ^{-1}(U)$, and let
$p \in \pi ^{-1}(U)$, and let ![]() $F, G \in \mathcal {O}_{M, p}^{\text {an}}$ be related to the germs
$F, G \in \mathcal {O}_{M, p}^{\text {an}}$ be related to the germs ![]() $f_{\pi (p)}, g_{\pi (p)} \in \mathcal {O}_{Q,\pi (p)}$ as in part (i). By definition, the germ of
$f_{\pi (p)}, g_{\pi (p)} \in \mathcal {O}_{Q,\pi (p)}$ as in part (i). By definition, the germ of ![]() $\{\pi ^{*}f, \pi ^{*}g\}'$ at
$\{\pi ^{*}f, \pi ^{*}g\}'$ at ![]() $p$ is
$p$ is ![]() $\{F, G\}\vert _N \in \mathcal {O}_{N, p}^{\mathrm {an}}$. It therefore suffices to show that
$\{F, G\}\vert _N \in \mathcal {O}_{N, p}^{\mathrm {an}}$. It therefore suffices to show that ![]() $\{F, G\}\vert _N$ is algebraic, i.e. that it lies in the image of the map
$\{F, G\}\vert _N$ is algebraic, i.e. that it lies in the image of the map ![]() $\mathcal {O}_{N, p} \longrightarrow \mathcal {O}_{N, p}^{\mathrm {an}}$.
$\mathcal {O}_{N, p} \longrightarrow \mathcal {O}_{N, p}^{\mathrm {an}}$.
Suppose that ![]() $X$ is affine for the moment. As
$X$ is affine for the moment. As ![]() $TS + \sigma (TS^{\circ })$ has constant rank, one may choose an algebraic subbundle
$TS + \sigma (TS^{\circ })$ has constant rank, one may choose an algebraic subbundle ![]() $R \subseteq TX\vert _{S}$ such that
$R \subseteq TX\vert _{S}$ such that
Remark 3.5 and the proof of Proposition 3.4 imply that there is a complex analytic Poisson transversal ![]() $Y \subseteq X$ such that
$Y \subseteq X$ such that
By [Reference Frejlich and MarcutFM17, Lemma 7], ![]() $Y$ and
$Y$ and ![]() $\mu$ are transverse and
$\mu$ are transverse and ![]() $P := \mu ^{-1}(Y)$ is a complex symplectic submanifold of
$P := \mu ^{-1}(Y)$ is a complex symplectic submanifold of ![]() $M$. It follows that
$M$. It follows that
is an algebraic subbundle of ![]() $TM\vert _N$ satisfying
$TM\vert _N$ satisfying
As ![]() $E$ is locally trivial, we may extend the projection
$E$ is locally trivial, we may extend the projection ![]() $E \oplus E^{\omega } \longrightarrow E$ to an algebraic section
$E \oplus E^{\omega } \longrightarrow E$ to an algebraic section ![]() $\theta$ of
$\theta$ of ![]() $\mathrm {End}(TM\vert _W)$ for some affine-open neighborhood
$\mathrm {End}(TM\vert _W)$ for some affine-open neighborhood ![]() $W$ of
$W$ of ![]() $p$.
$p$.
Noting that ![]() $F\vert _N = \pi ^{*}f$ and
$F\vert _N = \pi ^{*}f$ and ![]() $G\vert _N = \pi ^{*}g$ are algebraic, we may choose
$G\vert _N = \pi ^{*}g$ are algebraic, we may choose ![]() $\tilde {F}, \tilde {G} \in \mathcal {O}_{M, p}$ satisfying
$\tilde {F}, \tilde {G} \in \mathcal {O}_{M, p}$ satisfying ![]() $\tilde {F}\vert _N = F\vert _N$ and
$\tilde {F}\vert _N = F\vert _N$ and ![]() $\tilde {G}\vert _N = G\vert _N$. We claim that
$\tilde {G}\vert _N = G\vert _N$. We claim that
as germs in ![]() $\mathcal {O}_{N, p}^{\mathrm {an}}$. As the right-hand side is in
$\mathcal {O}_{N, p}^{\mathrm {an}}$. As the right-hand side is in ![]() $\mathcal {O}_{N, p}$, this would prove part (ii) in the case of an affine
$\mathcal {O}_{N, p}$, this would prove part (ii) in the case of an affine ![]() $X$.
$X$.
To verify (5.4), note that ![]() $N$ is coisotropic in
$N$ is coisotropic in ![]() $P$. We therefore have
$P$. We therefore have ![]() $TN^{\omega } \cap E \subseteq TN$, which in turn forces
$TN^{\omega } \cap E \subseteq TN$, which in turn forces ![]() $TN^{\omega } = D \oplus E^{\omega }$ to hold. It follows that
$TN^{\omega } = D \oplus E^{\omega }$ to hold. It follows that
i.e. ![]() $\theta (X_{\tilde {F}})$ is tangent to
$\theta (X_{\tilde {F}})$ is tangent to ![]() $N$. As
$N$. As ![]() $dF(TN^{\omega }) = 0$, we get that
$dF(TN^{\omega }) = 0$, we get that ![]() $\theta (X_{\tilde {F}}) - X_F$ is also tangent to
$\theta (X_{\tilde {F}}) - X_F$ is also tangent to ![]() $N$. On the other hand, the inclusion
$N$. On the other hand, the inclusion ![]() $TN \subseteq E$ tells us that
$TN \subseteq E$ tells us that
We conclude that ![]() $\theta (X_{\tilde {F}}) - X_F$ takes values in
$\theta (X_{\tilde {F}}) - X_F$ takes values in ![]() $TN \cap TN^{\omega } = D$ and, hence,
$TN \cap TN^{\omega } = D$ and, hence,
One then deduces that
 \begin{align*} \{F, G\}\vert_N &= \omega(X_{F}, X_{G})\vert_N = -dG(X_F)\vert_N = -d\tilde{G}(X_F)\vert_N = -d\tilde{G}(\theta(X_{\tilde{F}}))\vert_N = \omega(\theta(X_{\tilde{F}}), X_{\tilde{G}})\vert_N\\ &= \omega(\theta(X_{\tilde{F}}),\theta(X_{\tilde{G}}))\vert_N. \end{align*}
\begin{align*} \{F, G\}\vert_N &= \omega(X_{F}, X_{G})\vert_N = -dG(X_F)\vert_N = -d\tilde{G}(X_F)\vert_N = -d\tilde{G}(\theta(X_{\tilde{F}}))\vert_N = \omega(\theta(X_{\tilde{F}}), X_{\tilde{G}})\vert_N\\ &= \omega(\theta(X_{\tilde{F}}),\theta(X_{\tilde{G}}))\vert_N. \end{align*}
This proves part (ii) if ![]() $X$ is affine. For the general case, one simply chooses an affine-open neighborhood
$X$ is affine. For the general case, one simply chooses an affine-open neighborhood ![]() $V$ of
$V$ of ![]() $\mu (p)$ in
$\mu (p)$ in ![]() $X$ and repeats the argument with
$X$ and repeats the argument with ![]() $S$ and
$S$ and ![]() $X$ replaced by
$X$ replaced by ![]() $S \cap V$ and
$S \cap V$ and ![]() $V$, respectively.
$V$, respectively.
The proof of part (iii) is entirely analogous to that of Theorem 3.10(iii).
Definition 5.4 The Poisson variety ![]() $Q$ in Theorem 5.3 is called the symplectic reduction of
$Q$ in Theorem 5.3 is called the symplectic reduction of ![]() $M$ by
$M$ by ![]() $\mathcal {G}$ along
$\mathcal {G}$ along ![]() $S$ with respect to
$S$ with respect to ![]() $\mathcal {H}$ and
$\mathcal {H}$ and ![]() $\pi$. In this case, we denote
$\pi$. In this case, we denote ![]() $Q$ by
$Q$ by ![]() $M\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S,\mathcal {H},\pi }}\mathcal {G}$.
$M\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{S,\mathcal {H},\pi }}\mathcal {G}$.
Remark 5.5 Although the Poisson structure on ![]() $Q$ is algebraic, it may not always be possible to write
$Q$ is algebraic, it may not always be possible to write ![]() $\pi ^{*}\{f, g\}_Q = \{F, G\}\vert _N$ for algebraic functions
$\pi ^{*}\{f, g\}_Q = \{F, G\}\vert _N$ for algebraic functions ![]() $F, G$ satisfying part (i). To be more explicit, let
$F, G$ satisfying part (i). To be more explicit, let ![]() $((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$,
$((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$, ![]() $(S, \mathcal {H})$, and
$(S, \mathcal {H})$, and ![]() $\pi : N \longrightarrow Q$ be as in Theorem 5.3. Part (i) tells us that for all
$\pi : N \longrightarrow Q$ be as in Theorem 5.3. Part (i) tells us that for all ![]() $p \in N$ and
$p \in N$ and ![]() $f \in \mathcal {O}_{Q, \pi (p)}$, there exists an analytic germ
$f \in \mathcal {O}_{Q, \pi (p)}$, there exists an analytic germ ![]() $F \in \mathcal {O}_{M, p}^{\mathrm {an}}$ such that
$F \in \mathcal {O}_{M, p}^{\mathrm {an}}$ such that ![]() $\pi ^{*}f = F\vert _N$ and
$\pi ^{*}f = F\vert _N$ and ![]() $dF(TN^{\omega }) = 0$. It is natural to ask whether
$dF(TN^{\omega }) = 0$. It is natural to ask whether ![]() $F$ can be taken to be algebraic. This would certainly afford a more direct proof of the algebraicity of the Poisson bracket in part (ii) (cf. Remark 5.5). Although this approach works if
$F$ can be taken to be algebraic. This would certainly afford a more direct proof of the algebraicity of the Poisson bracket in part (ii) (cf. Remark 5.5). Although this approach works if ![]() $N$ is coisotropic, it fails in the general case. Indeed, finding
$N$ is coisotropic, it fails in the general case. Indeed, finding ![]() $F$ such that
$F$ such that ![]() $dF(TN^{\omega }) = 0$ is essentially solving a first-order partial differential equation; its solutions have no reason to be algebraic. To see this, consider the following example.
$dF(TN^{\omega }) = 0$ is essentially solving a first-order partial differential equation; its solutions have no reason to be algebraic. To see this, consider the following example.
Take ![]() $M=\mathbb {C}^{4}$ with coordinates
$M=\mathbb {C}^{4}$ with coordinates ![]() $(x, y, u, v)$ and symplectic form
$(x, y, u, v)$ and symplectic form ![]() $\omega = dx \wedge dy + du \wedge dv$. Consider the pair groupoid
$\omega = dx \wedge dy + du \wedge dv$. Consider the pair groupoid ![]() $\mathcal {G} := M \times M^{-}$ acting on
$\mathcal {G} := M \times M^{-}$ acting on ![]() $M$ with moment map the identity
$M$ with moment map the identity ![]() $M \longrightarrow M$ (cf. Example 2.28). Then
$M \longrightarrow M$ (cf. Example 2.28). Then ![]() $((M, \omega ), \mathcal {G} \rightrightarrows M, \mathrm {Id})$ is an algebraic Hamiltonian system. We claim that the subvariety
$((M, \omega ), \mathcal {G} \rightrightarrows M, \mathrm {Id})$ is an algebraic Hamiltonian system. We claim that the subvariety
is pre-Poisson.
Observe that ![]() $TS$ is spanned by
$TS$ is spanned by ![]() $\partial _x + 2x \partial _u$ and
$\partial _x + 2x \partial _u$ and ![]() $\partial _v$. We then find that
$\partial _v$. We then find that ![]() $TS^{\circ }$ is spanned by
$TS^{\circ }$ is spanned by ![]() $du - 2x\, dx$ and
$du - 2x\, dx$ and ![]() $dy$, and
$dy$, and ![]() $\omega (TS)$ is spanned by
$\omega (TS)$ is spanned by ![]() $dx + 2x\,dv$ and
$dx + 2x\,dv$ and ![]() $du$. It follows that the stabilizer subalgebroid
$du$. It follows that the stabilizer subalgebroid ![]() $L_S := \omega (TS) \cap TS^{\circ }$ of
$L_S := \omega (TS) \cap TS^{\circ }$ of ![]() $S$ is trivial, so that
$S$ is trivial, so that ![]() $S$ is pre-Poisson. The trivial groupoid
$S$ is pre-Poisson. The trivial groupoid ![]() $\mathcal {H}$ over
$\mathcal {H}$ over ![]() $S$ is then a stabilizer subgroupoid of
$S$ is then a stabilizer subgroupoid of ![]() $S$ in
$S$ in ![]() $\mathcal {G}$, and the identity map
$\mathcal {G}$, and the identity map ![]() $S \longrightarrow S$ is an algebraic quotient of
$S \longrightarrow S$ is an algebraic quotient of ![]() $S$ by
$S$ by ![]() $\mathcal {H}$. We are therefore in the context of Theorem 5.3.
$\mathcal {H}$. We are therefore in the context of Theorem 5.3.
On the other hand, we claim that there exist ![]() $p \in S$ and
$p \in S$ and ![]() $f \in \mathcal {O}_{S, p}$ such that there is no algebraic germ
$f \in \mathcal {O}_{S, p}$ such that there is no algebraic germ ![]() $F \in \mathcal {O}_{M, p}$ with
$F \in \mathcal {O}_{M, p}$ with ![]() $F\vert _S = f$ and
$F\vert _S = f$ and ![]() $dF(TS^{\omega }) = 0$. To this end, let
$dF(TS^{\omega }) = 0$. To this end, let ![]() $f : S \longrightarrow \mathbb {C}$ be given by
$f : S \longrightarrow \mathbb {C}$ be given by ![]() $f(x, y, u, v) = x$. Note that
$f(x, y, u, v) = x$. Note that ![]() $TS^{\omega }$ is spanned by
$TS^{\omega }$ is spanned by ![]() $2x \partial _y - \partial _v$ and
$2x \partial _y - \partial _v$ and ![]() $\partial _x$. It follows that a germ
$\partial _x$. It follows that a germ ![]() $F \in \mathcal {O}_{M, p}$ for
$F \in \mathcal {O}_{M, p}$ for ![]() $p \in S$ satisfies
$p \in S$ satisfies ![]() $dF(TS^{\omega }) = 0$ if and only if
$dF(TS^{\omega }) = 0$ if and only if
on ![]() $S$. Solving this partial differential equation with the constraint
$S$. Solving this partial differential equation with the constraint ![]() $F\vert _S = f$, e.g. by the method of characteristics, we find that
$F\vert _S = f$, e.g. by the method of characteristics, we find that
for any ![]() $g \in \mathcal {I}_S^{2}$, where
$g \in \mathcal {I}_S^{2}$, where ![]() $\mathcal {I}_S$ is the analytic ideal of
$\mathcal {I}_S$ is the analytic ideal of ![]() $S$ and the square root is defined by a branch of the logarithm such that
$S$ and the square root is defined by a branch of the logarithm such that ![]() $\sqrt {x^{2}} = x$ near
$\sqrt {x^{2}} = x$ near ![]() $p$. Note that
$p$. Note that ![]() $u \ne 0$ on
$u \ne 0$ on ![]() $S$, so
$S$, so ![]() $F$ is well-defined as a germ at
$F$ is well-defined as a germ at ![]() $p$. However, there is no
$p$. However, there is no ![]() $g \in \mathcal {I}_S^{2}$ such that
$g \in \mathcal {I}_S^{2}$ such that ![]() $\sqrt {u} + g$ is algebraic.
$\sqrt {u} + g$ is algebraic.
5.3 Poisson and hyperkähler slices
Suppose that ![]() $G$ is a connected complex semisimple linear algebraic group with Lie algebra
$G$ is a connected complex semisimple linear algebraic group with Lie algebra ![]() $\mathfrak {g}$. Use the Killing form to freely identify
$\mathfrak {g}$. Use the Killing form to freely identify ![]() $\mathfrak {g}$ and
$\mathfrak {g}$ and ![]() $\mathfrak {g}^{*}$ as
$\mathfrak {g}^{*}$ as ![]() $G$-modules. The Lie algebra
$G$-modules. The Lie algebra ![]() $\mathfrak {g}$ thereby inherits a Poisson variety structure from
$\mathfrak {g}$ thereby inherits a Poisson variety structure from ![]() $\mathfrak {g}^{*}$. At the same time, recall that
$\mathfrak {g}^{*}$. At the same time, recall that ![]() $\tau =(e,h,f)\in \mathfrak {g}^{3}$ is called an
$\tau =(e,h,f)\in \mathfrak {g}^{3}$ is called an ![]() $\mathfrak {sl}_2$-triple if the identities
$\mathfrak {sl}_2$-triple if the identities
hold in ![]() $\mathfrak {g}$. One then has an associated Slodowy slice
$\mathfrak {g}$. One then has an associated Slodowy slice
which is known to be a Poisson transversal in ![]() $\mathfrak {g}$ (see [Reference Gan and GinzburgGG02, Section 3.1]).
$\mathfrak {g}$ (see [Reference Gan and GinzburgGG02, Section 3.1]).
Fix an ![]() $\mathfrak {sl}_2$-triple
$\mathfrak {sl}_2$-triple ![]() $\tau \in \mathfrak {g}^{3}$ and suppose that
$\tau \in \mathfrak {g}^{3}$ and suppose that ![]() $\mu :M\longrightarrow \mathfrak {g}$ is a Hamiltonian
$\mu :M\longrightarrow \mathfrak {g}$ is a Hamiltonian ![]() $G$-variety, i.e. an algebraic Hamiltonian system
$G$-variety, i.e. an algebraic Hamiltonian system ![]() $((M, \omega ), \mathcal {G}\rightrightarrows X, \mu )$ with
$((M, \omega ), \mathcal {G}\rightrightarrows X, \mu )$ with ![]() $(\mathcal {G}\rightrightarrows X)=(T^{*}G\rightrightarrows \mathfrak {g})$. The previous paragraph and Example 2.27 tell us that
$(\mathcal {G}\rightrightarrows X)=(T^{*}G\rightrightarrows \mathfrak {g})$. The previous paragraph and Example 2.27 tell us that
is a symplectic subvariety of ![]() $M$, and that the trivial groupoid is a stabilizer subgroupoid of
$M$, and that the trivial groupoid is a stabilizer subgroupoid of ![]() $\mathcal {S}_{\tau }$. It follows that
$\mathcal {S}_{\tau }$. It follows that ![]() $M_{\tau }$ is the symplectic reduction of
$M_{\tau }$ is the symplectic reduction of ![]() $M$ by
$M$ by ![]() $T^{*}G\rightrightarrows \mathfrak {g}^{*}$ with respect to
$T^{*}G\rightrightarrows \mathfrak {g}^{*}$ with respect to ![]() $S_{\tau }$ and the trivial stabilizer subgroupoid
$S_{\tau }$ and the trivial stabilizer subgroupoid ![]() $\mathcal {H}\rightrightarrows \mathcal {S}_{\tau }$.
$\mathcal {H}\rightrightarrows \mathcal {S}_{\tau }$.
The symplectic variety ![]() $M\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{\mathcal {S}_{\tau }}}\mathcal {G}=M_{\tau }$ has been studied in each of the following contexts.
$M\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{\mathcal {S}_{\tau }}}\mathcal {G}=M_{\tau }$ has been studied in each of the following contexts.
(i) One obtains
 $M_{\tau }$ as a special case of the Poisson slice construction in [Reference Crooks and RöserCR20].
$M_{\tau }$ as a special case of the Poisson slice construction in [Reference Crooks and RöserCR20].(ii) If
 $M$ is hyperkähler and satisfies a mild condition, then
$M$ is hyperkähler and satisfies a mild condition, then  $M_{\tau }$ is hyperkähler [Reference BielawskiBie97, Theorem 1] and called a hyperkähler slice [Reference BielawskiBie17]. The study of hyperkähler slices originates in Bielawski's works [Reference BielawskiBie97, Reference BielawskiBie17] and occurs in the subsequent papers [Reference Crooks and RayanCR19, Reference Crooks and van PruijssenCP21].
$M_{\tau }$ is hyperkähler [Reference BielawskiBie97, Theorem 1] and called a hyperkähler slice [Reference BielawskiBie17]. The study of hyperkähler slices originates in Bielawski's works [Reference BielawskiBie97, Reference BielawskiBie17] and occurs in the subsequent papers [Reference Crooks and RayanCR19, Reference Crooks and van PruijssenCP21].(iii) Consider the symplectic manifold
 $T^{*}G$ equipped with the action of
$T^{*}G$ equipped with the action of  $G$ by right translations. One then finds that
$G$ by right translations. One then finds that  $(T^{*}G)_\tau = \mathfrak {M}_{G, \mathcal {S}_\tau } = G \times \mathcal {S}_\tau$. This symplectic subvariety of
$(T^{*}G)_\tau = \mathfrak {M}_{G, \mathcal {S}_\tau } = G \times \mathcal {S}_\tau$. This symplectic subvariety of  $T^{*}G$ is sometimes called a Nahm pole, and it receives considerable attention in [Reference BielawskiBie97, Reference Moore and TachikawaMT12, Reference BielawskiBie17, Reference Crooks and RayanCR19]. It enjoys a universal property, i.e.
$T^{*}G$ is sometimes called a Nahm pole, and it receives considerable attention in [Reference BielawskiBie97, Reference Moore and TachikawaMT12, Reference BielawskiBie17, Reference Crooks and RayanCR19]. It enjoys a universal property, i.e.  $M_\tau \cong (M \times (G \times \mathcal {S}_\tau ) \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{0}} G$ under certain hypotheses (see [Reference BielawskiBie17, Theorem 1(ii)] and [Reference Crooks and van PruijssenCP21, Proposition 4.2]). This can now be viewed as a special case of Theorem 4.11.
$M_\tau \cong (M \times (G \times \mathcal {S}_\tau ) \mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{0}} G$ under certain hypotheses (see [Reference BielawskiBie17, Theorem 1(ii)] and [Reference Crooks and van PruijssenCP21, Proposition 4.2]). This can now be viewed as a special case of Theorem 4.11.
5.4 The Moore–Tachikawa TQFT
Retain the Lie-theoretic objects and conventions established in the first paragraph of § 5.3. Consider the locus of regular elements
where ![]() $\ell$ is the rank of
$\ell$ is the rank of ![]() $\mathfrak {g}$ and
$\mathfrak {g}$ and ![]() $\mathfrak {g}_x\subseteq \mathfrak {g}$ denotes the
$\mathfrak {g}_x\subseteq \mathfrak {g}$ denotes the ![]() $\mathfrak {g}$-centralizer of
$\mathfrak {g}$-centralizer of ![]() $x\in \mathfrak {g}$. Let us also fix a principal
$x\in \mathfrak {g}$. Let us also fix a principal ![]() $\mathfrak {sl}_2$-triple, i.e. an
$\mathfrak {sl}_2$-triple, i.e. an ![]() $\mathfrak {sl}_2$-triple
$\mathfrak {sl}_2$-triple ![]() $\tau =(e, h, f)\in \mathfrak {g}^{3}$ for which
$\tau =(e, h, f)\in \mathfrak {g}^{3}$ for which ![]() $e,h,f\in \mathfrak {g}_{\text {reg}}$. The Slodowy slice
$e,h,f\in \mathfrak {g}_{\text {reg}}$. The Slodowy slice
is a fundamental domain for the action of ![]() $G$ on
$G$ on ![]() $\mathfrak {g}_{\text {reg}}$ (see [Reference KostantKos63, Theorem 8]), and it is a section of the adjoint quotient
$\mathfrak {g}_{\text {reg}}$ (see [Reference KostantKos63, Theorem 8]), and it is a section of the adjoint quotient
[Reference KostantKos63, Theorem 7]. This gives context for a conjecture of Moore–Tachikawa [Reference Moore and TachikawaMT12] and its appearances in the literature [Reference CalaqueCal15, Reference ArakawaAra19, Reference Braverman, Finkelberg and NakajimaBFN19, Reference BielawskiBie21].
Moore and Tachikawa [Reference Moore and TachikawaMT12] have conjectured the existence of certain topological quantum field theories (TQFTs) valued in ![]() $\mathrm {HS}$, the category of affine symplectic varieties with Hamiltonian actions. This category has complex semisimple linear algebraic groups as its objects. A morphism
$\mathrm {HS}$, the category of affine symplectic varieties with Hamiltonian actions. This category has complex semisimple linear algebraic groups as its objects. A morphism ![]() $H_1\longrightarrow H_2$ is an equivalence class of an affine symplectic
$H_1\longrightarrow H_2$ is an equivalence class of an affine symplectic ![]() $(H_1\times H_2\times \mathbb {C}^{\times })$-varietyFootnote 6 for which the symplectic form has
$(H_1\times H_2\times \mathbb {C}^{\times })$-varietyFootnote 6 for which the symplectic form has ![]() $\mathbb {C}^{\times }$-weight
$\mathbb {C}^{\times }$-weight ![]() $-2$ and the action of
$-2$ and the action of ![]() $H_1\times H_2$ is Hamiltonian; two such varieties are declared to be equivalent if they are
$H_1\times H_2$ is Hamiltonian; two such varieties are declared to be equivalent if they are ![]() $(H_1\times H_2\times \mathbb {C}^{\times })$-equivariantly symplectomorphic. In this context, one defines morphism composition as follows:
$(H_1\times H_2\times \mathbb {C}^{\times })$-equivariantly symplectomorphic. In this context, one defines morphism composition as follows:
for all ![]() $X_1\in \mathrm {Hom}_{\mathrm {HS}}(H_1,H_2)$ and
$X_1\in \mathrm {Hom}_{\mathrm {HS}}(H_1,H_2)$ and ![]() $X_2\in \mathrm {Hom}_{\mathrm {HS}}(H_2,H_3)$, where
$X_2\in \mathrm {Hom}_{\mathrm {HS}}(H_2,H_3)$, where ![]() $(X_1\times X_2)\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{}} H_2$ is the affine geometric invariant theory (GIT) quotient by
$(X_1\times X_2)\mkern -4mu\mathbin {/\mkern -5mu/}_{\mkern -4mu{}} H_2$ is the affine geometric invariant theory (GIT) quotient by ![]() $H_2$ of the zero-level set of the
$H_2$ of the zero-level set of the ![]() $H_2$-moment map on
$H_2$-moment map on ![]() $X_1\times X_2$. The identity object in
$X_1\times X_2$. The identity object in ![]() $\mathrm {Hom}_{\mathrm {HS}}(H,H)$ is then
$\mathrm {Hom}_{\mathrm {HS}}(H,H)$ is then ![]() $T^{*}H$, equipped with its usual Hamiltonian (
$T^{*}H$, equipped with its usual Hamiltonian (![]() $H\times H$)-action and its fiberwise dilation action of
$H\times H$)-action and its fiberwise dilation action of ![]() $\mathbb {C}^{\times }$.
$\mathbb {C}^{\times }$.
It turns out that ![]() $\mathrm {HS}$ is a symmetric monoidal category with duality; the symmetric monoidal structure is with respect to the usual products of linear algebraic groups and the usual products of affine symplectic varieties. The dual of
$\mathrm {HS}$ is a symmetric monoidal category with duality; the symmetric monoidal structure is with respect to the usual products of linear algebraic groups and the usual products of affine symplectic varieties. The dual of ![]() $H\in \mathrm {Ob}(\mathrm {HS})$ is defined to be
$H\in \mathrm {Ob}(\mathrm {HS})$ is defined to be ![]() $H$ itself, whereas the corresponding evaluation and coevaluation morphism are
$H$ itself, whereas the corresponding evaluation and coevaluation morphism are
respectively. On the other hand, one knows that two-dimensional cobordisms form a symmetric monoidal category ![]() $\mathrm {BO}_2$ with duality. These considerations lead to the following definition of Moore–Tachikawa [Reference Moore and TachikawaMT12].
$\mathrm {BO}_2$ with duality. These considerations lead to the following definition of Moore–Tachikawa [Reference Moore and TachikawaMT12].
Definition 5.6 A two-dimensional ![]() $\mathrm {HS}$-valued TQFT is a symmetric monoidal functor
$\mathrm {HS}$-valued TQFT is a symmetric monoidal functor ![]() $\eta :\mathrm {BO}_2\longrightarrow \mathrm {HS}$ that respects duality.
$\eta :\mathrm {BO}_2\longrightarrow \mathrm {HS}$ that respects duality.
Given a positive integer ![]() $n$, let
$n$, let
denote basic two-dimensional cobordism with ![]() $n$ incoming circles. The Moore–Tachikawa conjecture [Reference Moore and TachikawaMT12] is then formulated as follows.
$n$ incoming circles. The Moore–Tachikawa conjecture [Reference Moore and TachikawaMT12] is then formulated as follows.
Conjecture 5.7 If ![]() $G$ is a connected complex simple linear algebraic group, then there exists a two-dimensional
$G$ is a connected complex simple linear algebraic group, then there exists a two-dimensional ![]() $\mathrm {HS}$-valued TQFT
$\mathrm {HS}$-valued TQFT ![]() $\eta _G:\mathrm {BO}_2\longrightarrow \mathrm {HS}$ satisfying
$\eta _G:\mathrm {BO}_2\longrightarrow \mathrm {HS}$ satisfying ![]() $\eta _G(S^{1})=G$ and
$\eta _G(S^{1})=G$ and ![]() $\eta _G(C_1)=G\times \mathcal {S}$.
$\eta _G(C_1)=G\times \mathcal {S}$.
Remark 5.8 The condition ![]() $\eta _G(C_1)=G\times \mathcal {S}$ is imposed for physical reasons, as is explained in [Reference Moore and TachikawaMT12, Section 3.3].
$\eta _G(C_1)=G\times \mathcal {S}$ is imposed for physical reasons, as is explained in [Reference Moore and TachikawaMT12, Section 3.3].
Let ![]() $G$ be a connected complex simple linear algebraic group and
$G$ be a connected complex simple linear algebraic group and ![]() $\eta _G:\mathrm {BO}_2\longrightarrow \mathrm {HS}$ a TQFT satisfying Conjecture 5.7. The Hamiltonian
$\eta _G:\mathrm {BO}_2\longrightarrow \mathrm {HS}$ a TQFT satisfying Conjecture 5.7. The Hamiltonian ![]() $G^{n}$-varieties
$G^{n}$-varieties
are sometimes called Moore–Tachikawa varieties. Examples include ![]() $\eta _G(C_1)=G\times \mathcal {S}$ and
$\eta _G(C_1)=G\times \mathcal {S}$ and ![]() $\eta _G(C_2)=T^{*}G$, the second assertion being a straightforward consequence of Definition 5.6 and Conjecture 5.7. One also knows that the third Moore–Tachikawa variety
$\eta _G(C_2)=T^{*}G$, the second assertion being a straightforward consequence of Definition 5.6 and Conjecture 5.7. One also knows that the third Moore–Tachikawa variety ![]() $\eta _G(C_3)$ determines
$\eta _G(C_3)$ determines ![]() $\eta _G$ (see [Reference Moore and TachikawaMT12, Section 3.2]). Proving Conjecture 5.7 thereby amounts to finding a suitable candidate for
$\eta _G$ (see [Reference Moore and TachikawaMT12, Section 3.2]). Proving Conjecture 5.7 thereby amounts to finding a suitable candidate for ![]() $\eta _G(C_3)$.
$\eta _G(C_3)$.
Remark 5.9 The conjecture is known to be true for ![]() $G = \mathrm {SL}(2, \mathbb {C})$ and
$G = \mathrm {SL}(2, \mathbb {C})$ and ![]() $G = \mathrm {SL}(3, \mathbb {C})$ (see [Reference Moore and TachikawaMT12]). One has
$G = \mathrm {SL}(3, \mathbb {C})$ (see [Reference Moore and TachikawaMT12]). One has ![]() $\eta _{\mathrm {SL}(2, \mathbb {C})}(C_3) = \mathbb {C}^{2} \otimes \mathbb {C}^{2} \otimes \mathbb {C}^{2}$, whereas
$\eta _{\mathrm {SL}(2, \mathbb {C})}(C_3) = \mathbb {C}^{2} \otimes \mathbb {C}^{2} \otimes \mathbb {C}^{2}$, whereas ![]() $\eta _{\mathrm {SL}(3, \mathbb {C})}(C_3)$ is the closure of the minimal nilpotent orbit in the exceptional Lie algebra
$\eta _{\mathrm {SL}(3, \mathbb {C})}(C_3)$ is the closure of the minimal nilpotent orbit in the exceptional Lie algebra ![]() $E_6$.
$E_6$.
Ginzburg and Kazhdan [Reference Ginzburg and KazhdanGK] construct candidates for the Moore–Tachikawa varieties as follows. Recall our discussion in § 5.3(iii) of the symplectic subvariety
and adjoint quotient morphism ![]() $\chi :\mathfrak {g}\longrightarrow \mathfrak {c}$. One then defines the universal centralizer of
$\chi :\mathfrak {g}\longrightarrow \mathfrak {c}$. One then defines the universal centralizer of ![]() $G$ to be the closed subvariety
$G$ to be the closed subvariety
where ![]() $G_x\subseteq G$ denotes the
$G_x\subseteq G$ denotes the ![]() $G$-stabilizer of
$G$-stabilizer of ![]() $x\in \mathfrak {g}$. We have the morphism
$x\in \mathfrak {g}$. We have the morphism
and its restriction
to ![]() $\mathcal {J}$. The latter is an abelian group scheme over
$\mathcal {J}$. The latter is an abelian group scheme over ![]() $\mathfrak {c}$, and it acts on
$\mathfrak {c}$, and it acts on ![]() $\mathcal {N}$ via the map
$\mathcal {N}$ via the map
The kernel
of multiplication is then a group scheme over ![]() $\mathfrak {c}$ acting on
$\mathfrak {c}$ acting on
Ginzburg–Kazhdan [Reference Ginzburg and KazhdanGK] prove that ![]() $\mathcal {N} \times _\mathfrak {c} \cdots \times _\mathfrak {c} \mathcal {N}$ is coisotropic in
$\mathcal {N} \times _\mathfrak {c} \cdots \times _\mathfrak {c} \mathcal {N}$ is coisotropic in ![]() $\mathcal {N}^{n}$, and that the corresponding null-foliation is formed by the
$\mathcal {N}^{n}$, and that the corresponding null-foliation is formed by the ![]() $\mathcal {J}_n$-orbits. They also show the geometric quotient
$\mathcal {J}_n$-orbits. They also show the geometric quotient
to be a smooth algebraic variety, so that ![]() $\mathcal {Z}_n^{\circ }$ is necessarily symplectic. The left translation action of
$\mathcal {Z}_n^{\circ }$ is necessarily symplectic. The left translation action of ![]() $G^{n}$ on
$G^{n}$ on ![]() $T^{*}G^{n}$ then descends to a Hamiltonian
$T^{*}G^{n}$ then descends to a Hamiltonian ![]() $G^{n}$-action on
$G^{n}$-action on ![]() $\mathcal {Z}_n^{\circ }$.
$\mathcal {Z}_n^{\circ }$.
Ginzburg and Kazhdan subsequently define ![]() $\mathcal {Z}_n$ to be the affinization of
$\mathcal {Z}_n$ to be the affinization of ![]() $\mathcal {Z}_n^{\circ }$, i.e. the
$\mathcal {Z}_n^{\circ }$, i.e. the ![]() $G^{n}$-scheme
$G^{n}$-scheme
If ![]() $\mathbb {C}[\mathcal {N}_n]^{\mathcal {J}_n}$ is finitely generated for all
$\mathbb {C}[\mathcal {N}_n]^{\mathcal {J}_n}$ is finitely generated for all ![]() $n\geq 1$, then the
$n\geq 1$, then the ![]() $\mathcal {Z}_n$ are Moore–Tachikawa varieties that verify Conjecture 5.7 [Reference Ginzburg and KazhdanGK].
$\mathcal {Z}_n$ are Moore–Tachikawa varieties that verify Conjecture 5.7 [Reference Ginzburg and KazhdanGK].
Fix an integer ![]() $n\geq 1$ and let
$n\geq 1$ and let
denote the diagonally embedded copy of ![]() $\mathcal {S}$ in
$\mathcal {S}$ in ![]() $\mathfrak {g}^{n}$. We may identify
$\mathfrak {g}^{n}$. We may identify ![]() $\mathfrak {c}$ with
$\mathfrak {c}$ with ![]() $\mathcal {S}$ via the restricted adjoint quotient
$\mathcal {S}$ via the restricted adjoint quotient
and ![]() $\mathcal {S}$ with
$\mathcal {S}$ with ![]() $\Delta _n\mathcal {S}$ in the obvious way. The three varieties
$\Delta _n\mathcal {S}$ in the obvious way. The three varieties ![]() $\mathfrak {c}$,
$\mathfrak {c}$, ![]() $\mathcal {S}$, and
$\mathcal {S}$, and ![]() $\Delta _n\mathcal {S}$ are thereby treated interchangeably in what follows. One immediate consequence is our ability to view
$\Delta _n\mathcal {S}$ are thereby treated interchangeably in what follows. One immediate consequence is our ability to view ![]() $\mathcal {J}_n$ as a group scheme over
$\mathcal {J}_n$ as a group scheme over ![]() $\Delta _n\mathcal {S}$. At the same time, our identification
$\Delta _n\mathcal {S}$. At the same time, our identification ![]() $T^{*}G=G\times \mathfrak {g}$ induces a further identification
$T^{*}G=G\times \mathfrak {g}$ induces a further identification ![]() $T^{*}G^{n}=(G\times \mathfrak {g})^{n}$. The set-theoretic inclusion
$T^{*}G^{n}=(G\times \mathfrak {g})^{n}$. The set-theoretic inclusion ![]() $\mathcal {J}_n\subseteq (G\times \mathfrak {g})^{n}$ then renders
$\mathcal {J}_n\subseteq (G\times \mathfrak {g})^{n}$ then renders ![]() $\mathcal {J}_n\longrightarrow \Delta _n\mathcal {S}$ a subgroupoid of
$\mathcal {J}_n\longrightarrow \Delta _n\mathcal {S}$ a subgroupoid of ![]() $T^{*}G^{n}\rightrightarrows \mathfrak {g}^{n}$.
$T^{*}G^{n}\rightrightarrows \mathfrak {g}^{n}$.
Theorem 5.10 (Theorem E(i))
The following statements hold for all integers ![]() $n\geq 1$.
$n\geq 1$.
(i) The diagonal
 $\Delta _n\mathcal {S}\subseteq \mathfrak {g}^{n}$ is stableFootnote 7 and admits
$\Delta _n\mathcal {S}\subseteq \mathfrak {g}^{n}$ is stableFootnote 7 and admits  $\mathcal {J}_n$ as a stabilizer subgroupoid in
$\mathcal {J}_n$ as a stabilizer subgroupoid in  $T^{*}G^{n}\rightrightarrows \mathfrak {g}^{n}$.
$T^{*}G^{n}\rightrightarrows \mathfrak {g}^{n}$.(ii) We have
where \begin{align*} \mathcal{Z}_n^{\circ} = T^{*}G^{n} \mkern-4mu\mathbin{/\mkern-5mu/}_{\mkern-4mu{(\Delta_n\mathcal{S},\mathcal{J}_n,\pi_n)}} G^{n}, \end{align*}
\begin{align*} \mathcal{Z}_n^{\circ} = T^{*}G^{n} \mkern-4mu\mathbin{/\mkern-5mu/}_{\mkern-4mu{(\Delta_n\mathcal{S},\mathcal{J}_n,\pi_n)}} G^{n}, \end{align*} $\pi _n:\mathcal {N}_n\longrightarrow \mathcal {Z}_n^{\circ }$ is the geometric quotient map and
$\pi _n:\mathcal {N}_n\longrightarrow \mathcal {Z}_n^{\circ }$ is the geometric quotient map and  $G^{n}$ acts on
$G^{n}$ acts on  $T^{*}G^{n}$ by right translations.
$T^{*}G^{n}$ by right translations.(iii) Assume that
 $\mathbb {C}[\mathcal {N}_n]^{\mathcal {J}_n}$ is finitely generated. We have
where
$\mathbb {C}[\mathcal {N}_n]^{\mathcal {J}_n}$ is finitely generated. We have
where \begin{align*} \mathcal{Z}_n = T^{*}G^{n} \mkern-4mu\mathbin{/\mkern-5mu/}_{\mkern-4mu{(\Delta_n\mathcal{S},\mathcal{J}_n,\bar{\pi}_n)}} G^{n}, \end{align*}
\begin{align*} \mathcal{Z}_n = T^{*}G^{n} \mkern-4mu\mathbin{/\mkern-5mu/}_{\mkern-4mu{(\Delta_n\mathcal{S},\mathcal{J}_n,\bar{\pi}_n)}} G^{n}, \end{align*} $\bar {\pi }_n:\mathcal {N}_n\longrightarrow \mathcal {Z}_n$ is the affine GIT quotient map,
$\bar {\pi }_n:\mathcal {N}_n\longrightarrow \mathcal {Z}_n$ is the affine GIT quotient map,  $G^{n}$ acts on
$G^{n}$ acts on  $T^{*}G^{n}$ by right translations.
$T^{*}G^{n}$ by right translations.
Proof. Our arguments make extensive use of the fact that ![]() $\mathcal {S}$ is a transverse slice to the adjoint action [Reference Gan and GinzburgGG02, Section 3.1]. This amounts to the statement that
$\mathcal {S}$ is a transverse slice to the adjoint action [Reference Gan and GinzburgGG02, Section 3.1]. This amounts to the statement that
where we have identified ![]() $T_x\mathcal {S}$ with
$T_x\mathcal {S}$ with ![]() $\mathfrak {g}_f$ and
$\mathfrak {g}_f$ and ![]() $T_x(G \cdot x)$ with
$T_x(G \cdot x)$ with ![]() $[\mathfrak {g}, x]$.
$[\mathfrak {g}, x]$.
Lemma 4.4 implies that
for all ![]() $\underline {x} = (x, \ldots, x) \in \Delta _n \mathcal {S}$, where
$\underline {x} = (x, \ldots, x) \in \Delta _n \mathcal {S}$, where ![]() $\mathfrak {g}_f^{\perp }$ is the annihilator of
$\mathfrak {g}_f^{\perp }$ is the annihilator of ![]() $\mathfrak {g}_f$ under the Killing form. On the other hand (5.5) tells us that
$\mathfrak {g}_f$ under the Killing form. On the other hand (5.5) tells us that ![]() $\mathfrak {g}_f \cap [\mathfrak {g}, x] = 0$ for all
$\mathfrak {g}_f \cap [\mathfrak {g}, x] = 0$ for all ![]() $x\in \mathcal {S}$. One consequence is as follows: if
$x\in \mathcal {S}$. One consequence is as follows: if ![]() $[x, y_i] \in \mathfrak {g}_f$, then
$[x, y_i] \in \mathfrak {g}_f$, then ![]() $[x, y_i] = 0$, i.e.
$[x, y_i] = 0$, i.e. ![]() $y_i \in \mathfrak {g}_x$. Equation (5.5) also implies that
$y_i \in \mathfrak {g}_x$. Equation (5.5) also implies that ![]() $\mathfrak {g}_f^{\perp } \cap \mathfrak {g}_x = (\mathfrak {g}_f + [\mathfrak {g}, x])^{\perp } = 0$. These considerations and the observation that
$\mathfrak {g}_f^{\perp } \cap \mathfrak {g}_x = (\mathfrak {g}_f + [\mathfrak {g}, x])^{\perp } = 0$. These considerations and the observation that
give
for all ![]() $x \in \mathcal {S}$, where
$x \in \mathcal {S}$, where ![]() $(\mathcal {J}_n)_{\underline {x}}$ is the fiber of
$(\mathcal {J}_n)_{\underline {x}}$ is the fiber of ![]() $\mathcal {J}_n$ over
$\mathcal {J}_n$ over ![]() $\underline {x} \in \Delta _n\mathcal {S}$. We also know that
$\underline {x} \in \Delta _n\mathcal {S}$. We also know that ![]() $\dim \mathfrak {g}_x = \dim \mathfrak {g}_y$ for all
$\dim \mathfrak {g}_x = \dim \mathfrak {g}_y$ for all ![]() $x, y \in \mathcal {S}$, as
$x, y \in \mathcal {S}$, as ![]() $\mathcal {S} \subseteq \mathfrak {g}_{\mathrm {reg}}$. It follows that
$\mathcal {S} \subseteq \mathfrak {g}_{\mathrm {reg}}$. It follows that ![]() $\dim (L_{\Delta _n\mathcal {S}})_{\underline {x}}$ is independent of
$\dim (L_{\Delta _n\mathcal {S}})_{\underline {x}}$ is independent of ![]() $x \in \mathcal {S}$, i.e.
$x \in \mathcal {S}$, i.e. ![]() $\Delta _n\mathcal {S}$ is pre-Poisson. We also see that
$\Delta _n\mathcal {S}$ is pre-Poisson. We also see that ![]() $(L_{\Delta _n\mathcal {S}})_{\underline {x}} \subseteq (\mathfrak {g}_x)^{n}$ for all
$(L_{\Delta _n\mathcal {S}})_{\underline {x}} \subseteq (\mathfrak {g}_x)^{n}$ for all ![]() $x \in \mathcal {S}$, so that
$x \in \mathcal {S}$, so that ![]() $\Delta _n\mathcal {S}$ is stable.
$\Delta _n\mathcal {S}$ is stable.
In light of (5.7) and Theorem 4.17(i)–(iii), showing ![]() $(\mathcal {J}_n)_{\underline {x}}$ to be connected for all
$(\mathcal {J}_n)_{\underline {x}}$ to be connected for all ![]() $x$ in an open dense subset of
$x$ in an open dense subset of ![]() $\mathcal {S}$ will force
$\mathcal {S}$ will force ![]() $\mathcal {J}_n$ to be a stabilizer subgroupoid of
$\mathcal {J}_n$ to be a stabilizer subgroupoid of ![]() $\Delta _n\mathcal {S}$. To this end, (5.6) tells us that
$\Delta _n\mathcal {S}$. To this end, (5.6) tells us that ![]() $(\mathcal {J}_n)_{\underline {x}} \cong (G_x)^{n - 1}$ for all
$(\mathcal {J}_n)_{\underline {x}} \cong (G_x)^{n - 1}$ for all ![]() $x\in \mathcal {S}$. We also know
$x\in \mathcal {S}$. We also know ![]() $G_x$ to be a maximal torus if
$G_x$ to be a maximal torus if ![]() $x\in \mathcal {S}$ is semisimple. It follows that
$x\in \mathcal {S}$ is semisimple. It follows that ![]() $(\mathcal {J}_n)_{\underline {x}}$ is indeed connected for all
$(\mathcal {J}_n)_{\underline {x}}$ is indeed connected for all ![]() $x$ in an open dense subset of
$x$ in an open dense subset of ![]() $x$, completing the proof of part (i).
$x$, completing the proof of part (i).
To establish the remaining parts, consider (4.2). This implies that the moment map for the action of ![]() $G^{n}$ on
$G^{n}$ on ![]() $T^{*}G^{n}$ by right translations is
$T^{*}G^{n}$ by right translations is
A further observation is that
Parts (ii) and (iii) then follow immediately from the definitions of ![]() $\mathcal {Z}_n^{\circ }$ and
$\mathcal {Z}_n^{\circ }$ and ![]() $\mathcal {Z}_n$, respectively.
$\mathcal {Z}_n$, respectively.
Remark 5.11 If ![]() $G$ is of adjoint type, then the
$G$ is of adjoint type, then the ![]() $G$-stabilizers of regular elements are connected. It follows that
$G$-stabilizers of regular elements are connected. It follows that ![]() $\mathcal {J}_n$ is a source-connected stabilizer subgroupoid of
$\mathcal {J}_n$ is a source-connected stabilizer subgroupoid of ![]() $\Delta _n\mathcal {S}$ in
$\Delta _n\mathcal {S}$ in ![]() $T^{*}G^{n} \rightrightarrows \mathfrak {g}^{n}$. We thereby obtain the simplified expressions
$T^{*}G^{n} \rightrightarrows \mathfrak {g}^{n}$. We thereby obtain the simplified expressions
where ![]() $(\mathfrak {M}_{G^{n}, \Delta _n\mathcal {S}})^{\mathrm {aff}}$ is the affinization of
$(\mathfrak {M}_{G^{n}, \Delta _n\mathcal {S}})^{\mathrm {aff}}$ is the affinization of ![]() $\mathfrak {M}_{G^{n}, \Delta _n\mathcal {S}}$.
$\mathfrak {M}_{G^{n}, \Delta _n\mathcal {S}}$.
6. Shifted symplectic interpretation
We now interpret the notion of symplectic reduction along a submanifold in the context of shifted symplectic geometry [Reference Pantev, Toën, Vaquié and VezzosiPTVV13]. More precisely, we view our construction as a derived intersection of two Lagrangians in a 1-shifted symplectic stack and obtain a ![]() $0$-shifted symplectic structure from [Reference Pantev, Toën, Vaquié and VezzosiPTVV13, Theorem 2.9]. There are similar statements in the literature for Marsden–Weinstein–Meyer reduction [Reference Calaque, Anel and CatrenCal20, § 2.1.2] and quasi-Hamiltonian reduction [Reference SafronovSaf16]. We refer the reader to [Reference Pantev, Toën, Vaquié and VezzosiPTVV13, Reference GetzlerGet14, Reference Calaque, Anel and CatrenCal20, Reference Pym and SafronovPS20] for the relevant background on shifted symplectic geometry.
$0$-shifted symplectic structure from [Reference Pantev, Toën, Vaquié and VezzosiPTVV13, Theorem 2.9]. There are similar statements in the literature for Marsden–Weinstein–Meyer reduction [Reference Calaque, Anel and CatrenCal20, § 2.1.2] and quasi-Hamiltonian reduction [Reference SafronovSaf16]. We refer the reader to [Reference Pantev, Toën, Vaquié and VezzosiPTVV13, Reference GetzlerGet14, Reference Calaque, Anel and CatrenCal20, Reference Pym and SafronovPS20] for the relevant background on shifted symplectic geometry.
Given an algebraic symplectic groupoid ![]() $\mathcal {G} \rightrightarrows X$, recall that the quotient stack
$\mathcal {G} \rightrightarrows X$, recall that the quotient stack ![]() $[X/\mathcal {G}]$ inherits a
$[X/\mathcal {G}]$ inherits a ![]() $1$-shifted symplectic structure (see e.g. [Reference Calaque, Anel and CatrenCal20, § 1.2.3], [Reference GetzlerGet14], and [Reference SafronovSaf21, Proposition 3.31]). Recall also that a Hamiltonian action of
$1$-shifted symplectic structure (see e.g. [Reference Calaque, Anel and CatrenCal20, § 1.2.3], [Reference GetzlerGet14], and [Reference SafronovSaf21, Proposition 3.31]). Recall also that a Hamiltonian action of ![]() $\mathcal {G} \rightrightarrows X$ on a smooth symplectic variety
$\mathcal {G} \rightrightarrows X$ on a smooth symplectic variety ![]() $(M, \omega )$ with moment map
$(M, \omega )$ with moment map ![]() $\mu : M \longrightarrow X$ gives rise to a Lagrangian structure on the map
$\mu : M \longrightarrow X$ gives rise to a Lagrangian structure on the map ![]() $[\mu ] : [M/\mathcal {G}] \longrightarrow [X/\mathcal {G}]$ (see [Reference Calaque, Anel and CatrenCal20, Example 1.31]).
$[\mu ] : [M/\mathcal {G}] \longrightarrow [X/\mathcal {G}]$ (see [Reference Calaque, Anel and CatrenCal20, Example 1.31]).
Consider a Lie subgroupoid ![]() $\mathcal {H} \rightrightarrows S$ of
$\mathcal {H} \rightrightarrows S$ of ![]() $\mathcal {G} \rightrightarrows X$ with morphism
$\mathcal {G} \rightrightarrows X$ with morphism ![]() $f : \mathcal {H} \longrightarrow \mathcal {G}$. An isotropic structure on
$f : \mathcal {H} \longrightarrow \mathcal {G}$. An isotropic structure on ![]() $[f] : [S / \mathcal {H}] \longrightarrow [X/\mathcal {G}]$ is a closed 2-form
$[f] : [S / \mathcal {H}] \longrightarrow [X/\mathcal {G}]$ is a closed 2-form ![]() $\beta$ on
$\beta$ on ![]() $S$ such that
$S$ such that ![]() $f^{*}\Omega = \mathsf {s}^{*}\beta - \mathsf {t}^{*}\beta,$ where
$f^{*}\Omega = \mathsf {s}^{*}\beta - \mathsf {t}^{*}\beta,$ where ![]() $\Omega$ is the symplectic form on
$\Omega$ is the symplectic form on ![]() $\mathcal {G}$ (see [Reference Pantev, Toën, Vaquié and VezzosiPTVV13, Definition 2.7] or [Reference Calaque, Anel and CatrenCal20, § 1.3.2]). The isotropic structure
$\mathcal {G}$ (see [Reference Pantev, Toën, Vaquié and VezzosiPTVV13, Definition 2.7] or [Reference Calaque, Anel and CatrenCal20, § 1.3.2]). The isotropic structure ![]() $\beta$ is called Lagrangian if the induced morphism
$\beta$ is called Lagrangian if the induced morphism ![]() $\mathbb {T}_f \longrightarrow \mathbb {L}_{[S/\mathcal {H}]}$ is a quasi-isomorphism [Reference Pantev, Toën, Vaquié and VezzosiPTVV13, Definition 2.8], where
$\mathbb {T}_f \longrightarrow \mathbb {L}_{[S/\mathcal {H}]}$ is a quasi-isomorphism [Reference Pantev, Toën, Vaquié and VezzosiPTVV13, Definition 2.8], where ![]() $\mathbb {T}$ and
$\mathbb {T}$ and ![]() $\mathbb {L}$ denote the tangent and cotangent complexes, respectively, and
$\mathbb {L}$ denote the tangent and cotangent complexes, respectively, and
is the relative tangent complex with the differential given by the map ![]() $\mathbb {T}_{[S/\mathcal {H}]} \to f^{*}\mathbb {T}_{[X/\mathcal {G}]}$.
$\mathbb {T}_{[S/\mathcal {H}]} \to f^{*}\mathbb {T}_{[X/\mathcal {G}]}$.
Proposition 6.1 (Theorem G(i))
Let ![]() $\mathcal {H} \rightrightarrows S$ be a Lie subgroupoid of an algebraic symplectic groupoid
$\mathcal {H} \rightrightarrows S$ be a Lie subgroupoid of an algebraic symplectic groupoid ![]() $\mathcal {G} \rightrightarrows X$. The zero 2-form on
$\mathcal {G} \rightrightarrows X$. The zero 2-form on ![]() $S$ is a Lagrangian structure on
$S$ is a Lagrangian structure on ![]() $[S / \mathcal {H}] \longrightarrow [X / \mathcal {G}]$ if and only if
$[S / \mathcal {H}] \longrightarrow [X / \mathcal {G}]$ if and only if ![]() $\mathcal {H}$ is the stabilizer subgroupoid of a pre-Poisson submanifold.
$\mathcal {H}$ is the stabilizer subgroupoid of a pre-Poisson submanifold.
Proof. Note that ![]() $\beta = 0$ is an isotropic structure if and only if
$\beta = 0$ is an isotropic structure if and only if ![]() $\mathcal {H}$ is isotropic in
$\mathcal {H}$ is isotropic in ![]() $\mathcal {G}$. We may therefore assume that
$\mathcal {G}$. We may therefore assume that ![]() $\mathcal {H}$ is isotropic, and aim to show that the trivial isotropic structure on
$\mathcal {H}$ is isotropic, and aim to show that the trivial isotropic structure on ![]() $[f] : [S/\mathcal {H}] \longrightarrow [X/\mathcal {G}]$ is Lagrangian if and only if the Lie algebroid
$[f] : [S/\mathcal {H}] \longrightarrow [X/\mathcal {G}]$ is Lagrangian if and only if the Lie algebroid ![]() $L$ of
$L$ of ![]() $\mathcal {H}$, viewed as a subalgebroid of
$\mathcal {H}$, viewed as a subalgebroid of ![]() $T^{*}X = \operatorname {Lie}(\mathcal {G})$, is equal to
$T^{*}X = \operatorname {Lie}(\mathcal {G})$, is equal to ![]() $\sigma ^{-1}(TS) \cap TS^{\circ }$, where
$\sigma ^{-1}(TS) \cap TS^{\circ }$, where ![]() $\sigma : T^{*}X \longrightarrow TX$ is the Poisson structure.
$\sigma : T^{*}X \longrightarrow TX$ is the Poisson structure.
Recall that the tangent complex of the quotient stack of a groupoid is the two-term complex given by the anchor map in degrees ![]() $-1$ and
$-1$ and ![]() $0$ (see e.g. [Reference Calaque, Anel and CatrenCal20, § 1.2.3]). It follows that the map of complexes
$0$ (see e.g. [Reference Calaque, Anel and CatrenCal20, § 1.2.3]). It follows that the map of complexes ![]() $\mathbb {T}_f \longrightarrow \mathbb {L}_{[S/\mathcal {H}]}$ is given by
$\mathbb {T}_f \longrightarrow \mathbb {L}_{[S/\mathcal {H}]}$ is given by

where the maps are defined as follows:
–
 $\alpha$ is the sum of the inclusion
$\alpha$ is the sum of the inclusion  $L \longrightarrow T^{*}X\vert _S$ and the anchor map
$L \longrightarrow T^{*}X\vert _S$ and the anchor map  $\sigma _L : L \longrightarrow TS$;
$\sigma _L : L \longrightarrow TS$;–
 $\beta$ is the sum of
$\beta$ is the sum of  $\sigma$ and the inclusion
$\sigma$ and the inclusion  $TS \longrightarrow TX\vert _S$;
$TS \longrightarrow TX\vert _S$;–
 $\gamma$ is the sum of the restriction map
$\gamma$ is the sum of the restriction map  $T^{*}X\vert _S \longrightarrow T^{*}S$ and the map
$T^{*}X\vert _S \longrightarrow T^{*}S$ and the map  $TS \longrightarrow T^{*}S$ given by the isotropic structure (which is zero in this case);
$TS \longrightarrow T^{*}S$ given by the isotropic structure (which is zero in this case);–
 $\delta$ is the restriction map;
$\delta$ is the restriction map;–
 $\varepsilon$ is the dual of the anchor map
$\varepsilon$ is the dual of the anchor map  $\sigma _L$ of
$\sigma _L$ of  $L$.
$L$.
As ![]() $\mathcal {H}$ is isotropic in
$\mathcal {H}$ is isotropic in ![]() $\mathcal {G}$, we have
$\mathcal {G}$, we have ![]() $L \subseteq TS^{\circ }$ and this diagram commutes.
$L \subseteq TS^{\circ }$ and this diagram commutes.
Passing to the map on cohomologies, we obtain

The trivial isotropic structure is Lagrangian if and only if ![]() $\varphi$ and
$\varphi$ and ![]() $\psi$ are isomorphisms. Note that
$\psi$ are isomorphisms. Note that
Hence, if the isotropic structure is Lagrangian, then ![]() $L = \sigma ^{-1}(TS) \cap TS$. Conversely, suppose that
$L = \sigma ^{-1}(TS) \cap TS$. Conversely, suppose that ![]() $L = \sigma ^{-1}(TS) \cap TS^{\circ }$. We then have
$L = \sigma ^{-1}(TS) \cap TS^{\circ }$. We then have ![]() $\ker \varphi = 0$ by (6.1). By identifying
$\ker \varphi = 0$ by (6.1). By identifying ![]() $\mathrm {Ann}_{T^{*}S}(\sigma (L))$ with
$\mathrm {Ann}_{T^{*}S}(\sigma (L))$ with ![]() $\sigma (L)^{\circ } / TS^{\circ }$, the image of
$\sigma (L)^{\circ } / TS^{\circ }$, the image of ![]() $\varphi$ is
$\varphi$ is ![]() $\sigma ^{-1}(TS) / TS^{\circ }$. However,
$\sigma ^{-1}(TS) / TS^{\circ }$. However,
so ![]() $\sigma (L)^{\circ } / TS^{\circ } = \sigma ^{-1}(TS) / TS^{\circ }$ and, hence,
$\sigma (L)^{\circ } / TS^{\circ } = \sigma ^{-1}(TS) / TS^{\circ }$ and, hence, ![]() $\varphi$ is surjective. On the other hand, note that
$\varphi$ is surjective. On the other hand, note that
It follows that ![]() $\psi$ is an isomorphism if and only if
$\psi$ is an isomorphism if and only if
The latter equality holds because ![]() $L^{\circ } = (\sigma ^{-1}(TS) \cap TS^{\circ })^{\circ } = \sigma (TS^{\circ }) + TS$.
$L^{\circ } = (\sigma ^{-1}(TS) \cap TS^{\circ })^{\circ } = \sigma (TS^{\circ }) + TS$.
By combining Proposition 6.1 and [Reference Pantev, Toën, Vaquié and VezzosiPTVV13, Theorem 2.9], we obtain the following result.
Theorem 6.2 (Theorem G(ii))
Let ![]() $((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$ be an algebraic Hamiltonian system,
$((M, \omega ), \mathcal {G} \rightrightarrows X, \mu )$ be an algebraic Hamiltonian system, ![]() $S \subseteq X$ a pre-Poisson subvariety, and
$S \subseteq X$ a pre-Poisson subvariety, and ![]() $\mathcal {H} \rightrightarrows S$ a stabilizer subgroupoid of
$\mathcal {H} \rightrightarrows S$ a stabilizer subgroupoid of ![]() $S$ in
$S$ in ![]() $\mathcal {G}$. Then the derived fiber product
$\mathcal {G}$. Then the derived fiber product
has a canonical ![]() $0$-shifted symplectic structure.
$0$-shifted symplectic structure.
Example 6.3 If ![]() $\mathcal {G} \rightrightarrows X$ in Theorem 6.2 is a cotangent groupoid
$\mathcal {G} \rightrightarrows X$ in Theorem 6.2 is a cotangent groupoid ![]() $T^{*}G \rightrightarrows \mathfrak {g}^{*}$ and
$T^{*}G \rightrightarrows \mathfrak {g}^{*}$ and ![]() $S = \{0\}$, we recover the derived version of Marsden–Weinstein–Meyer reduction at level zero [Reference Calaque, Anel and CatrenCal20, § 2.1.2].
$S = \{0\}$, we recover the derived version of Marsden–Weinstein–Meyer reduction at level zero [Reference Calaque, Anel and CatrenCal20, § 2.1.2].
Notation

Acknowledgements
We gratefully acknowledge Victor Ginzburg for sending us a draft of joint work with David Kazhdan [Reference Ginzburg and KazhdanGK]. We also thank Justin Hilburn, Steven Rayan, and Marco Zambon for fruitful conversations, as well as the referees for extremely constructive and substantive feedback.