Article contents
Serre weights for quaternion algebras
Published online by Cambridge University Press: 09 February 2011
Abstract
We study the possible weights of an irreducible two-dimensional mod p representation of 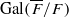 which is modular in the sense that it comes from an automorphic form on a definite quaternion algebra with centre F which is ramified at all places dividing p, where F is a totally real field. In most cases we determine the precise list of possible weights; in the remaining cases we determine the possible weights up to a short and explicit list of exceptions.
which is modular in the sense that it comes from an automorphic form on a definite quaternion algebra with centre F which is ramified at all places dividing p, where F is a totally real field. In most cases we determine the precise list of possible weights; in the remaining cases we determine the possible weights up to a short and explicit list of exceptions.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © Foundation Compositio Mathematica 2011
References
- 6
- Cited by


