Hostname: page-component-76fb5796d-x4r87 Total loading time: 0 Render date: 2024-04-25T11:33:45.285Z Has data issue: false hasContentIssue false
  • English
  • Français

Self-dual integral normal bases and Galois module structure

Part of: Algebraic number theory: local and $p$-adic fields Algebraic number theory: global fields

Published online by Cambridge University Press:  10 May 2013

Erik Jarl Pickett  and
Stéphane Vinatier
Erik Jarl Pickett
Affiliation:
53 Parkfield Crescent, Kimpton, Herts, SG4 8EQ, UK email erik_pickett@hotmail.com
Stéphane Vinatier
Affiliation:
XLIM-DMI, 123 avenue Albert Thomas, 87060 Limoges, France email stephane.vinatier@unilim.fr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 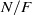$N/ F$ be an odd-degree Galois extension of number fields with Galois group 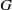$G$ and rings of integers 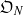${\mathfrak{O}}_{N} $ and 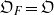${\mathfrak{O}}_{F} = \mathfrak{O}$. Let 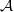$ \mathcal{A} $ be the unique fractional 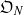${\mathfrak{O}}_{N} $-ideal with square equal to the inverse different of 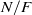$N/ F$. B. Erez showed that 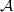$ \mathcal{A} $ is a locally free 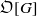$\mathfrak{O}[G] $-module if and only if 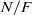$N/ F$ is a so-called weakly ramified extension. Although a number of results have been proved regarding the freeness of 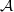$ \mathcal{A} $ as a 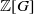$ \mathbb{Z} [G] $-module, the question remains open. In this paper we prove that 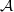$ \mathcal{A} $ is free as a 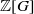$ \mathbb{Z} [G] $-module provided that 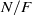$N/ F$ is weakly ramified and under the hypothesis that for every prime 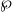$\wp $ of 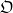$\mathfrak{O}$ which ramifies wildly in 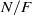$N/ F$, the decomposition group is abelian, the ramification group is cyclic and 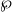$\wp $ is unramified in 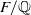$F/ \mathbb{Q} $. We make crucial use of a construction due to the first author which uses Dwork’s exponential power series to describe self-dual integral normal bases in Lubin–Tate extensions of local fields. This yields a new and striking relationship between the local norm-resolvent and the Galois Gauss sum involved. Our results generalise work of the second author concerning the case of base field 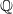$ \mathbb{Q} $.

Keywords

Galois modulesquare root of the inverse differentweakly ramified extensionsDwork’s power seriesself-dual integral normal basisGalois Gauss sum

MSC classification

Secondary: 11R04: Algebraic numbers; rings of algebraic integers 11R33: Integral representations related to algebraic numbers; Galois module structure of rings of integers 11S31: Class field theory; $p$-adic formal groups 11R20: Other abelian and metabelian extensions 11R29: Class numbers, class groups, discriminants 11R32: Galois theory 11S15: Ramification and extension theory 11S20: Galois theory 11S80: Other analytic theory (analogues of beta and gamma functions, $p$-adic integration, etc.)
Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 7 , July 2013 , pp. 1175 - 1202
Copyright
© The Author(s) 2013 

References

Cassou-Noguès, P. and Taylor, M. J., Opérations d’Adams et groupe des classes d’algèbre de groupe, J. Algebra 95 (1985), 125–152.Google Scholar
Dwork, B., On the zeta functions of a hypersurface. II, Ann. of Math. (2) 80 (1964), 227–299.Google Scholar
Erez, B., The Galois structure of the square root of the inverse different, Math. Z. 208 (1991), 239–255.Google Scholar
Fesenko, I. B. and Vostokov, S. V., Local fields and their extensions, second edition (American Mathematical Society, Providence, RI, 2002).Google Scholar
Fröhlich, A., Galois module structure of algebraic integers (Springer, Berlin, 1983).Google Scholar
Iwasawa, K., Local class field theory (Oxford University Press, Oxford, 1986).Google Scholar
Koblitz, N., p-adic numbers, p-adic analysis, and zeta-functions, Graduate Texts in Mathematics, vol. 58 (Springer, New York, 1977).Google Scholar
Lang, S., Cyclotomic fields II (Springer, New York, 1980).Google Scholar
Martinet, J., Character theory and Artin $L$-functions, in Algebraic number fields: L-functions and Galois properties, Proceedings of a Symposium at the University of Durham, 1975 (Academic Press, London, 1977), 1–87.Google Scholar
Pickett, E. J., Explicit construction of self-dual integral normal bases for the square-root of the inverse different, J. Number Theory 129 (2009), 1773–1785.Google Scholar
Pickett, E. J., Construction of self-dual integral normal bases in abelian extensions of finite and local fields, Int. J. Number Theory 6 (2010), 1565–1588.Google Scholar
Serre, J. P., Local class field theory, in Algebraic number theory, eds Cassels, J. W. S. and Fröhlich, A. (Academic Press, London, 1967).Google Scholar
Serre, J. P., Corps locaux (Hermann, Paris, 1968).Google Scholar
Tate, J. T., Local constants, in Algebraic number fields: L-functions and Galois properties, Proceedings of a Symposium at the University of Durham, 1975 (Academic Press, London, 1977), 89–131, Prepared in collaboration with C. J. Bushnell and M. J. Taylor.Google Scholar
Taylor, M. J., On Fröhlich’s conjecture for rings of integers of tame extensions, Invent. Math. 63 (1981), 41–79.Google Scholar
Vinatier, S., Structure galoisienne dans les extensions faiblement ramifiées de $ \mathbb{Q} $, J. Number Theory 91 (2001), 126–152.Google Scholar
Vinatier, S., Galois module structure in weakly ramified 3-extensions, Acta Arith. 119 (2005), 171–186.CrossRefGoogle Scholar