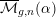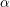1 Introduction
This is the second paper in a trilogy in which we construct the second flip in the log minimal model program for
![]() $\overline{M}_{g,n}$
. In this paper, we prove that the moduli stacks
$\overline{M}_{g,n}$
. In this paper, we prove that the moduli stacks
 $\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC})$
parameterizing
$\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC})$
parameterizing
![]() $\unicode[STIX]{x1D6FC}$
-stable curves introduced in [Reference Alper, Fedorchuk, Smyth and van der WyckAFSvdW17, § 2] admit good moduli spaces. Namely, we prove the following result.
$\unicode[STIX]{x1D6FC}$
-stable curves introduced in [Reference Alper, Fedorchuk, Smyth and van der WyckAFSvdW17, § 2] admit good moduli spaces. Namely, we prove the following result.
Theorem 1.1. For every
 $\unicode[STIX]{x1D6FC}\in (2/3-\unicode[STIX]{x1D716},1]$
,
$\unicode[STIX]{x1D6FC}\in (2/3-\unicode[STIX]{x1D716},1]$
,
 $\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC})$
admits a good moduli space
$\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC})$
admits a good moduli space
 $\overline{\mathbb{M}}_{g,n}(\unicode[STIX]{x1D6FC})$
which is a proper algebraic space over
$\overline{\mathbb{M}}_{g,n}(\unicode[STIX]{x1D6FC})$
which is a proper algebraic space over
![]() $\mathbb{C}$
. Furthermore, for each critical value
$\mathbb{C}$
. Furthermore, for each critical value
 $\unicode[STIX]{x1D6FC}_{c}\in \{2/3,7/10,9/11\}$
, there exists a diagram
$\unicode[STIX]{x1D6FC}_{c}\in \{2/3,7/10,9/11\}$
, there exists a diagram

where
 $\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})\rightarrow \overline{\mathbb{M}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
,
$\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})\rightarrow \overline{\mathbb{M}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
,
 $\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c}+\unicode[STIX]{x1D716})\rightarrow \overline{\mathbb{M}}_{g,n}(\unicode[STIX]{x1D6FC}_{c}+\unicode[STIX]{x1D716})$
, and
$\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c}+\unicode[STIX]{x1D716})\rightarrow \overline{\mathbb{M}}_{g,n}(\unicode[STIX]{x1D6FC}_{c}+\unicode[STIX]{x1D716})$
, and
 $\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c}-\unicode[STIX]{x1D716})\rightarrow \overline{\mathbb{M}}_{g,n}(\unicode[STIX]{x1D6FC}_{c}-\unicode[STIX]{x1D716})$
are good moduli spaces, and where
$\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c}-\unicode[STIX]{x1D716})\rightarrow \overline{\mathbb{M}}_{g,n}(\unicode[STIX]{x1D6FC}_{c}-\unicode[STIX]{x1D716})$
are good moduli spaces, and where
 $\overline{\mathbb{M}}_{g,n}(\unicode[STIX]{x1D6FC}_{c}+\unicode[STIX]{x1D716})\rightarrow \overline{\mathbb{M}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
and
$\overline{\mathbb{M}}_{g,n}(\unicode[STIX]{x1D6FC}_{c}+\unicode[STIX]{x1D716})\rightarrow \overline{\mathbb{M}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
and
 $\overline{\mathbb{M}}_{g,n}(\unicode[STIX]{x1D6FC}_{c}-\unicode[STIX]{x1D716})\rightarrow \overline{\mathbb{M}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
are proper morphisms of algebraic spaces.
$\overline{\mathbb{M}}_{g,n}(\unicode[STIX]{x1D6FC}_{c}-\unicode[STIX]{x1D716})\rightarrow \overline{\mathbb{M}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
are proper morphisms of algebraic spaces.
The goal of the final paper in the trilogy [Reference Alper, Fedorchuk and SmythAFS16] is to establish an isomorphism between
 $\overline{\mathbb{M}}_{g,n}(\unicode[STIX]{x1D6FC})$
and the projective variety
$\overline{\mathbb{M}}_{g,n}(\unicode[STIX]{x1D6FC})$
and the projective variety
 $$\begin{eqnarray}\displaystyle \overline{M}_{g,n}(\unicode[STIX]{x1D6FC}):=\operatorname{Proj}\bigoplus _{m\geqslant 0}\text{H}^{0}(\overline{{\mathcal{M}}}_{g,n},\lfloor m(K_{\overline{{\mathcal{M}}}_{g,n}}+\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FF}+(1-\unicode[STIX]{x1D6FC})\unicode[STIX]{x1D713})\rfloor ), & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \overline{M}_{g,n}(\unicode[STIX]{x1D6FC}):=\operatorname{Proj}\bigoplus _{m\geqslant 0}\text{H}^{0}(\overline{{\mathcal{M}}}_{g,n},\lfloor m(K_{\overline{{\mathcal{M}}}_{g,n}}+\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FF}+(1-\unicode[STIX]{x1D6FC})\unicode[STIX]{x1D713})\rfloor ), & & \displaystyle\end{eqnarray}$$
which thereby proves that the good moduli spaces of
 $\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC})$
are indeed the log canonical models defined in (1.1).
$\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC})$
are indeed the log canonical models defined in (1.1).
In the case where
 $\unicode[STIX]{x1D6FC}\in (2/3,7/10]$
and
$\unicode[STIX]{x1D6FC}\in (2/3,7/10]$
and
![]() $n=0$
, the spaces
$n=0$
, the spaces
 $\overline{\mathbb{M}}_{g,n}(\unicode[STIX]{x1D6FC})$
have been constructed using geometric invariant theory (GIT) by Hassett and Hyeon in [Reference Hassett and HyeonHH09, Reference Hassett and HyeonHH13]. There is no known GIT construction of the moduli spaces corresponding to
$\overline{\mathbb{M}}_{g,n}(\unicode[STIX]{x1D6FC})$
have been constructed using geometric invariant theory (GIT) by Hassett and Hyeon in [Reference Hassett and HyeonHH09, Reference Hassett and HyeonHH13]. There is no known GIT construction of the moduli spaces corresponding to
 $\unicode[STIX]{x1D6FC}\leqslant 2/3$
. Thus, this paper gives the first intrinsic construction of a moduli space associated to an algebraic stack parameterizing objects with infinite automorphism groups.
$\unicode[STIX]{x1D6FC}\leqslant 2/3$
. Thus, this paper gives the first intrinsic construction of a moduli space associated to an algebraic stack parameterizing objects with infinite automorphism groups.
In order to prove Theorem 1.1, we establish three general existence results for good moduli spaces. These existence results make essential use of the notions of local quotient presentation and variation of geometric invariant theory (VGIT) chambers of a local quotient presentation, introduced in Definitions 2.1 and 2.4, respectively. Our first existence result gives conditions under which one may use a local quotient presentation to construct a good moduli space.
Theorem 1.2. Let
![]() ${\mathcal{X}}$
be an algebraic stack of finite type over an algebraically closed field
${\mathcal{X}}$
be an algebraic stack of finite type over an algebraically closed field
![]() $k$
. Suppose that:
$k$
. Suppose that:
-
(1) for every closed point
 $x\in {\mathcal{X}}$
, there exists a local quotient presentation
$x\in {\mathcal{X}}$
, there exists a local quotient presentation
 $f:{\mathcal{W}}\rightarrow {\mathcal{X}}$
around
$f:{\mathcal{W}}\rightarrow {\mathcal{X}}$
around
 $x$
such that:
$x$
such that:-
(a) the morphism
 $f$
is stabilizer preserving at closed points of
$f$
is stabilizer preserving at closed points of
 ${\mathcal{W}}$
; and
${\mathcal{W}}$
; and -
(b) the morphism
 $f$
sends closed points to closed points; and
$f$
sends closed points to closed points; and
-
-
(2) for any point
 $x\in {\mathcal{X}}(k)$
, the closed substack
$x\in {\mathcal{X}}(k)$
, the closed substack
 $\overline{\{x\}}$
admits a good moduli space.
$\overline{\{x\}}$
admits a good moduli space.
Then
![]() ${\mathcal{X}}$
admits a good moduli space.
${\mathcal{X}}$
admits a good moduli space.
As we explain below, this result may be considered as an analog of the Keel–Mori theorem [Reference Keel and MoriKM97] for algebraic stacks, but in practice the hypotheses of Theorem 1.2 are harder to verify than those of the Keel–Mori theorem. Nevertheless, we believe that the above theorem should be applicable to many additional moduli problems. In fact, it has come to our attention that it has already been applied to construct a good moduli space of Kähler–Einstein Fano varieties in [Reference Li, Wang and XuLWX14, Reference OdakaOda15].
Our second existence result, Theorem 1.3, gives one situation in which the hypotheses of Theorem 1.2 are satisfied. It says that if
![]() ${\mathcal{X}}$
is an algebraic stack and
${\mathcal{X}}$
is an algebraic stack and
 ${\mathcal{X}}^{+}{\hookrightarrow}{\mathcal{X}}{\hookleftarrow}{\mathcal{X}}^{-}$
is a pair of open immersions locally cut out by VGIT chambers of a local quotient presentation, then
${\mathcal{X}}^{+}{\hookrightarrow}{\mathcal{X}}{\hookleftarrow}{\mathcal{X}}^{-}$
is a pair of open immersions locally cut out by VGIT chambers of a local quotient presentation, then
![]() ${\mathcal{X}}$
admits a good moduli space if
${\mathcal{X}}$
admits a good moduli space if
![]() ${\mathcal{X}}^{+}$
,
${\mathcal{X}}^{+}$
,
 ${\mathcal{X}}\smallsetminus {\mathcal{X}}^{+}$
, and
${\mathcal{X}}\smallsetminus {\mathcal{X}}^{+}$
, and
 ${\mathcal{X}}\smallsetminus {\mathcal{X}}^{-}$
do.
${\mathcal{X}}\smallsetminus {\mathcal{X}}^{-}$
do.
Theorem 1.3. Let
![]() ${\mathcal{X}}$
be an algebraic stack of finite type over an algebraically closed field
${\mathcal{X}}$
be an algebraic stack of finite type over an algebraically closed field
![]() $k$
and let
$k$
and let
![]() ${\mathcal{L}}$
be a line bundle on
${\mathcal{L}}$
be a line bundle on
![]() ${\mathcal{X}}$
. Let
${\mathcal{X}}$
. Let
 ${\mathcal{X}}^{+},{\mathcal{X}}^{-}\subset {\mathcal{X}}$
be open substacks, and let
${\mathcal{X}}^{+},{\mathcal{X}}^{-}\subset {\mathcal{X}}$
be open substacks, and let
 ${\mathcal{Z}}^{+}={\mathcal{X}}\smallsetminus {\mathcal{X}}^{+}$
,
${\mathcal{Z}}^{+}={\mathcal{X}}\smallsetminus {\mathcal{X}}^{+}$
,
 ${\mathcal{Z}}^{-}={\mathcal{X}}\smallsetminus {\mathcal{X}}^{-}$
be their reduced complements. Suppose that:
${\mathcal{Z}}^{-}={\mathcal{X}}\smallsetminus {\mathcal{X}}^{-}$
be their reduced complements. Suppose that:
-
(i) the algebraic stacks
 ${\mathcal{X}}^{+}$
,
${\mathcal{X}}^{+}$
,
 ${\mathcal{Z}}^{+}$
,
${\mathcal{Z}}^{+}$
,
 ${\mathcal{Z}}^{-}$
admit good moduli spaces; and
${\mathcal{Z}}^{-}$
admit good moduli spaces; and -
(ii) for all closed points
 $x\in {\mathcal{Z}}^{+}\cap {\mathcal{Z}}^{-}$
, there exist a local quotient presentation
$x\in {\mathcal{Z}}^{+}\cap {\mathcal{Z}}^{-}$
, there exist a local quotient presentation
 $f:{\mathcal{W}}\rightarrow {\mathcal{X}}$
around
$f:{\mathcal{W}}\rightarrow {\mathcal{X}}$
around
 $x$
and a Cartesian diagram(1.2)where
$x$
and a Cartesian diagram(1.2)where
 ${\mathcal{W}}_{{\mathcal{L}}}^{+},{\mathcal{W}}_{{\mathcal{L}}}^{-}$
are the VGIT chambers of
${\mathcal{W}}_{{\mathcal{L}}}^{+},{\mathcal{W}}_{{\mathcal{L}}}^{-}$
are the VGIT chambers of
 ${\mathcal{W}}$
with respect to
${\mathcal{W}}$
with respect to
 ${\mathcal{L}}$
.
${\mathcal{L}}$
.
Then there exist good moduli spaces
 ${\mathcal{X}}\rightarrow X$
and
${\mathcal{X}}\rightarrow X$
and
 ${\mathcal{X}}^{-}\rightarrow X^{-}$
such that
${\mathcal{X}}^{-}\rightarrow X^{-}$
such that
 $X^{+}\rightarrow X$
and
$X^{+}\rightarrow X$
and
 $X^{-}\rightarrow X$
are proper and surjective. In particular, if
$X^{-}\rightarrow X$
are proper and surjective. In particular, if
![]() $X^{+}$
is proper over
$X^{+}$
is proper over
![]() $k$
, then
$k$
, then
![]() $X$
and
$X$
and
![]() $X^{-}$
are also proper over
$X^{-}$
are also proper over
![]() $k$
.
$k$
.
The third existence result, Proposition 1.4, proves that one can check existence of a good moduli space after passing to a finite cover by a quotient stack. Recall that an algebraic stack
![]() ${\mathcal{X}}$
is called a global quotient stack if
${\mathcal{X}}$
is called a global quotient stack if
 ${\mathcal{Z}}\simeq [Z/\text{GL}_{n}]$
, where
${\mathcal{Z}}\simeq [Z/\text{GL}_{n}]$
, where
![]() $Z$
is an algebraic space with an action of
$Z$
is an algebraic space with an action of
![]() $\operatorname{GL}_{n}$
.
$\operatorname{GL}_{n}$
.
Proposition 1.4. Let
 $f:{\mathcal{X}}\rightarrow {\mathcal{Y}}$
be a morphism of algebraic stacks of finite type over an algebraically closed field
$f:{\mathcal{X}}\rightarrow {\mathcal{Y}}$
be a morphism of algebraic stacks of finite type over an algebraically closed field
![]() $k$
of characteristic
$k$
of characteristic
![]() $0$
. Suppose that:
$0$
. Suppose that:
-
(i) the morphism
 $f:{\mathcal{X}}\rightarrow {\mathcal{Y}}$
is finite and surjective;
$f:{\mathcal{X}}\rightarrow {\mathcal{Y}}$
is finite and surjective; -
(ii) there exists a good moduli space
 ${\mathcal{X}}\rightarrow X$
with
${\mathcal{X}}\rightarrow X$
with
 $X$
separated; and
$X$
separated; and -
(iii) the algebraic stack
 ${\mathcal{Y}}$
is a global quotient stack and admits local quotient presentations.
${\mathcal{Y}}$
is a global quotient stack and admits local quotient presentations.
Then there exists a good moduli space
![]() ${\mathcal{Y}}\rightarrow Y$
with
${\mathcal{Y}}\rightarrow Y$
with
![]() $Y$
separated. Moreover, if
$Y$
separated. Moreover, if
![]() $X$
is proper, so is
$X$
is proper, so is
![]() $Y$
.
$Y$
.
Both Theorem 1.3 and Proposition 1.4 are proved using Theorem 1.2.
1.1 Motivation and sketch of proof of Theorem 1.2
In order to motivate the statement of Theorem 1.2, let us give an informal sketch of the proof. If
![]() ${\mathcal{X}}$
admits local quotient presentations, then every closed point
${\mathcal{X}}$
admits local quotient presentations, then every closed point
![]() $x\in {\mathcal{X}}$
admits an étale and affine neighborhood of the form
$x\in {\mathcal{X}}$
admits an étale and affine neighborhood of the form
 $$\begin{eqnarray}[\operatorname{Spec}A_{x}/G_{x}]\rightarrow {\mathcal{X}},\end{eqnarray}$$
$$\begin{eqnarray}[\operatorname{Spec}A_{x}/G_{x}]\rightarrow {\mathcal{X}},\end{eqnarray}$$
where
![]() $A_{x}$
is a
$A_{x}$
is a
![]() $k$
-algebra of finite type and
$k$
-algebra of finite type and
![]() $G_{x}$
is the stabilizer of
$G_{x}$
is the stabilizer of
![]() $x$
. The union
$x$
. The union
 $$\begin{eqnarray}\coprod _{x\in {\mathcal{X}}}[\operatorname{Spec}A_{x}/G_{x}]\end{eqnarray}$$
$$\begin{eqnarray}\coprod _{x\in {\mathcal{X}}}[\operatorname{Spec}A_{x}/G_{x}]\end{eqnarray}$$
defines an étale cover of
![]() ${\mathcal{X}}$
; reducing to a finite subcover, we obtain an atlas
${\mathcal{X}}$
; reducing to a finite subcover, we obtain an atlas
 $f:{\mathcal{W}}\rightarrow {\mathcal{X}}$
with the following properties:
$f:{\mathcal{W}}\rightarrow {\mathcal{X}}$
with the following properties:
-
(i)
 $f$
is étale and affine; and
$f$
is étale and affine; and -
(ii)
 ${\mathcal{W}}$
admits a good moduli space
${\mathcal{W}}$
admits a good moduli space
 $W$
.
$W$
.
Indeed, (ii) follows simply by taking invariants
 $[\operatorname{Spec}A_{x}/G_{x}]\rightarrow \operatorname{Spec}A_{x}^{G_{x}}$
. Since
$[\operatorname{Spec}A_{x}/G_{x}]\rightarrow \operatorname{Spec}A_{x}^{G_{x}}$
. Since
![]() $f$
is affine, the fiber product
$f$
is affine, the fiber product
 ${\mathcal{R}}:={\mathcal{W}}\times _{{\mathcal{X}}}{\mathcal{W}}$
admits a good moduli space
${\mathcal{R}}:={\mathcal{W}}\times _{{\mathcal{X}}}{\mathcal{W}}$
admits a good moduli space
![]() $R$
. We may thus consider the following diagram:
$R$
. We may thus consider the following diagram:

The crucial question is: can we choose
 $f:{\mathcal{W}}\rightarrow {\mathcal{X}}$
to guarantee that the projections
$f:{\mathcal{W}}\rightarrow {\mathcal{X}}$
to guarantee that the projections
 $q_{1},q_{2}:R\rightrightarrows W$
define an étale equivalence relation? If so, then the algebraic space quotient
$q_{1},q_{2}:R\rightrightarrows W$
define an étale equivalence relation? If so, then the algebraic space quotient
 $X=W/R$
gives a good moduli space for
$X=W/R$
gives a good moduli space for
![]() ${\mathcal{X}}$
.
${\mathcal{X}}$
.
If
![]() ${\mathcal{X}}$
is a separated Deligne–Mumford stack, we can always do this. Indeed, the atlas
${\mathcal{X}}$
is a separated Deligne–Mumford stack, we can always do this. Indeed, the atlas
![]() $f$
may be chosen to be stabilizer preserving.Footnote
1
Thus, we may take the projections
$f$
may be chosen to be stabilizer preserving.Footnote
1
Thus, we may take the projections
 ${\mathcal{R}}\rightrightarrows {\mathcal{W}}$
to be stabilizer preserving and étale, and this implies that the projections
${\mathcal{R}}\rightrightarrows {\mathcal{W}}$
to be stabilizer preserving and étale, and this implies that the projections
 $R\rightrightarrows W$
are étale.Footnote
2
This leads to a direct proof of the Keel–Mori theorem for separated Deligne–Mumford stacks of finite type over
$R\rightrightarrows W$
are étale.Footnote
2
This leads to a direct proof of the Keel–Mori theorem for separated Deligne–Mumford stacks of finite type over
![]() $\operatorname{Spec}k$
(one can show directly that such stacks always admit local quotient presentations). In general, of course, algebraic stacks need not be separated so we must find weaker conditions which ensure that the projections
$\operatorname{Spec}k$
(one can show directly that such stacks always admit local quotient presentations). In general, of course, algebraic stacks need not be separated so we must find weaker conditions which ensure that the projections
![]() $q_{1},q_{2}$
are étale. In particular, we must identify a set of sufficient conditions that can be directly verified for geometrically defined stacks such as
$q_{1},q_{2}$
are étale. In particular, we must identify a set of sufficient conditions that can be directly verified for geometrically defined stacks such as
 $\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC})$
.
$\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC})$
.
Our result gives at least one plausible answer to this problem. To begin, note that if
![]() $\unicode[STIX]{x1D714}\in {\mathcal{W}}$
is a closed
$\unicode[STIX]{x1D714}\in {\mathcal{W}}$
is a closed
![]() $k$
-point with image
$k$
-point with image
![]() $w\in W$
, then the formal neighborhood
$w\in W$
, then the formal neighborhood
![]() $\widehat{{\mathcal{O}}}_{W,w}$
can be identified with the
$\widehat{{\mathcal{O}}}_{W,w}$
can be identified with the
![]() $G_{\unicode[STIX]{x1D714}}$
-invariants
$G_{\unicode[STIX]{x1D714}}$
-invariants
![]() $D_{\unicode[STIX]{x1D714}}^{G_{\unicode[STIX]{x1D714}}}$
of the miniversal deformation space
$D_{\unicode[STIX]{x1D714}}^{G_{\unicode[STIX]{x1D714}}}$
of the miniversal deformation space
![]() $D_{\unicode[STIX]{x1D714}}$
of
$D_{\unicode[STIX]{x1D714}}$
of
![]() $\unicode[STIX]{x1D714}$
. Thus, we may ensure that
$\unicode[STIX]{x1D714}$
. Thus, we may ensure that
![]() $q_{i}$
is étale at a
$q_{i}$
is étale at a
![]() $k$
-point
$k$
-point
![]() $r\in R$
, or equivalently that the induced map
$r\in R$
, or equivalently that the induced map
 $\widehat{{\mathcal{O}}}_{W,q_{i}(r)}\rightarrow \widehat{{\mathcal{O}}}_{R,r}$
is an isomorphism, by manually imposing the following conditions:
$\widehat{{\mathcal{O}}}_{W,q_{i}(r)}\rightarrow \widehat{{\mathcal{O}}}_{R,r}$
is an isomorphism, by manually imposing the following conditions:
![]() $p_{i}(\unicode[STIX]{x1D70C})$
should be a closed point, where
$p_{i}(\unicode[STIX]{x1D70C})$
should be a closed point, where
![]() $\unicode[STIX]{x1D70C}\in {\mathcal{R}}$
is the unique closed point in the preimage of
$\unicode[STIX]{x1D70C}\in {\mathcal{R}}$
is the unique closed point in the preimage of
![]() $r\in R$
, and
$r\in R$
, and
![]() $p_{i}$
should induce an isomorphism of stabilizer groups
$p_{i}$
should induce an isomorphism of stabilizer groups
 $G_{\unicode[STIX]{x1D70C}}\simeq G_{p_{i}(\unicode[STIX]{x1D70C})}$
. Indeed, we then have
$G_{\unicode[STIX]{x1D70C}}\simeq G_{p_{i}(\unicode[STIX]{x1D70C})}$
. Indeed, we then have
 $\widehat{{\mathcal{O}}}_{W,q_{i}(r)}=D_{p_{i}(\unicode[STIX]{x1D70C})}^{G_{p_{i}(\unicode[STIX]{x1D70C})}}\simeq D_{\unicode[STIX]{x1D70C}}^{G_{\unicode[STIX]{x1D70C}}}=\widehat{{\mathcal{O}}}_{R,r}$
, where the middle isomorphism follows from the hypothesis that
$\widehat{{\mathcal{O}}}_{W,q_{i}(r)}=D_{p_{i}(\unicode[STIX]{x1D70C})}^{G_{p_{i}(\unicode[STIX]{x1D70C})}}\simeq D_{\unicode[STIX]{x1D70C}}^{G_{\unicode[STIX]{x1D70C}}}=\widehat{{\mathcal{O}}}_{R,r}$
, where the middle isomorphism follows from the hypothesis that
![]() $p_{i}$
is étale and stabilizer preserving. In sum, we have identified two key conditions that will imply that
$p_{i}$
is étale and stabilizer preserving. In sum, we have identified two key conditions that will imply that
 $R\rightrightarrows W$
is an étale equivalence relation:
$R\rightrightarrows W$
is an étale equivalence relation:
-
 $(\star )$
$(\star )$
-
the morphism
 $f:{\mathcal{W}}\rightarrow {\mathcal{X}}$
is stabilizer preserving at closed points;
$f:{\mathcal{W}}\rightarrow {\mathcal{X}}$
is stabilizer preserving at closed points; -
 $(\star \star )$
$(\star \star )$
-
the projections
 $p_{1},p_{2}:{\mathcal{W}}\times _{{\mathcal{X}}}{\mathcal{W}}\rightrightarrows {\mathcal{W}}$
send closed points to closed points.
$p_{1},p_{2}:{\mathcal{W}}\times _{{\mathcal{X}}}{\mathcal{W}}\rightrightarrows {\mathcal{W}}$
send closed points to closed points.
Condition (
![]() $\star$
) is precisely hypothesis (1a) of Theorem 1.2. In practice, it is difficult to directly verify condition (
$\star$
) is precisely hypothesis (1a) of Theorem 1.2. In practice, it is difficult to directly verify condition (
![]() $\star \star$
), but it turns out that it is implied by conditions (1b) and (2) of Theorem 1.2, which are often easier to verify.
$\star \star$
), but it turns out that it is implied by conditions (1b) and (2) of Theorem 1.2, which are often easier to verify.
1.2 Roadmap
In § 2, we recall the necessary terminology and results from [Reference Alper, Fedorchuk, Smyth and van der WyckAFSvdW17]. We also prove some preliminary lemmas concerning strongly étale morphisms. In § 3, we prove Theorems 1.2 and 1.3 and Proposition 1.4. Namely, in § 3.1, we prove Theorem 1.2 along the lines described in § 1.1. Then we prove Theorem 1.3 and Proposition 1.4 in §§ 3.2 and 3.3, respectively, by showing that after suitable reductions, their hypotheses imply that conditions (1a), (1b), and (2) of Theorem 1.2 are satisfied. In § 4, we apply Theorem 1.3 to prove Theorem 1.1. Appendix A provides various examples of algebraic stacks highlighting the necessity of conditions (1a), (1b), and (2) in Theorem 1.2.
Notation
Theorem 1.1 holds over an arbitrary algebraically closed field
![]() $\mathbb{C}$
of characteristic
$\mathbb{C}$
of characteristic
![]() $0$
. In §§ 2 and 3, we work over an algebraically closed field
$0$
. In §§ 2 and 3, we work over an algebraically closed field
![]() $k$
of arbitrary characteristic unless when stated otherwise. A linearly reductive group scheme over a field
$k$
of arbitrary characteristic unless when stated otherwise. A linearly reductive group scheme over a field
![]() $k$
is, by definition, an affine group scheme of finite type over
$k$
is, by definition, an affine group scheme of finite type over
![]() $k$
such that every representation is completely reducible.
$k$
such that every representation is completely reducible.
2 Background and preliminary results
2.1 Local quotient presentations
Definition 2.1. Let
![]() ${\mathcal{X}}$
be an algebraic stack of finite type over an algebraically closed field
${\mathcal{X}}$
be an algebraic stack of finite type over an algebraically closed field
![]() $k$
and let
$k$
and let
 $x\in {\mathcal{X}}(k)$
be a closed point. We say that
$x\in {\mathcal{X}}(k)$
be a closed point. We say that
 $f:{\mathcal{W}}\rightarrow {\mathcal{X}}$
is a local quotient presentation around
$f:{\mathcal{W}}\rightarrow {\mathcal{X}}$
is a local quotient presentation around
![]() $x$
if:
$x$
if:
-
(i) the stabilizer
 $G_{x}$
of
$G_{x}$
of
 $x$
is linearly reductive;
$x$
is linearly reductive; -
(ii) there is an isomorphism
 ${\mathcal{W}}\simeq [\operatorname{Spec}A/G_{x}]$
, where
${\mathcal{W}}\simeq [\operatorname{Spec}A/G_{x}]$
, where
 $A$
is a
$A$
is a
 $k$
-algebra of finite type;
$k$
-algebra of finite type; -
(iii) the morphism
 $f$
is étale and affine; and
$f$
is étale and affine; and -
(iv) there exists a point
 $w\in {\mathcal{W}}(k)$
such that
$w\in {\mathcal{W}}(k)$
such that
 $f(w)=x$
and
$f(w)=x$
and
 $f$
induces an isomorphism of stabilizer group schemes at
$f$
induces an isomorphism of stabilizer group schemes at
 $x$
.
$x$
.
We sometimes write
 $f:({\mathcal{W}},w)\rightarrow ({\mathcal{X}},x)$
as a local quotient presentation to indicate the chosen preimage of
$f:({\mathcal{W}},w)\rightarrow ({\mathcal{X}},x)$
as a local quotient presentation to indicate the chosen preimage of
![]() $x$
. We say that
$x$
. We say that
![]() ${\mathcal{X}}$
admits local quotient presentations if there exist local quotient presentations around all closed points
${\mathcal{X}}$
admits local quotient presentations if there exist local quotient presentations around all closed points
 $x\in {\mathcal{X}}(k)$
.
$x\in {\mathcal{X}}(k)$
.
Remark 2.2. Note that if
![]() ${\mathcal{X}}$
admits local quotient presentations, then
${\mathcal{X}}$
admits local quotient presentations, then
![]() ${\mathcal{X}}$
necessarily has affine diagonal and every closed point necessarily has a linearly reductive stabilizer group.
${\mathcal{X}}$
necessarily has affine diagonal and every closed point necessarily has a linearly reductive stabilizer group.
For our purpose of applying Theorem 1.3 to the moduli stacks
 $\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC})$
, the following result suffices to guarantee the existence of local quotient presentations.
$\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC})$
, the following result suffices to guarantee the existence of local quotient presentations.
Proposition 2.3 [Reference Alper and KreschAK16, § 3.3].
Let
![]() $k$
be an algebraically closed field. Let
$k$
be an algebraically closed field. Let
![]() ${\mathcal{X}}$
be a quotient stack
${\mathcal{X}}$
be a quotient stack
![]() $[U/G]$
, where
$[U/G]$
, where
![]() $U$
is a normal and separated scheme of finite type over
$U$
is a normal and separated scheme of finite type over
![]() $k$
and
$k$
and
![]() $G$
is a smooth linear algebraic group over
$G$
is a smooth linear algebraic group over
![]() $k$
. If
$k$
. If
 $x\in {\mathcal{X}}(k)$
is a point with linearly reductive stabilizer, then there exists a local quotient presentation
$x\in {\mathcal{X}}(k)$
is a point with linearly reductive stabilizer, then there exists a local quotient presentation
 $f:{\mathcal{W}}\rightarrow {\mathcal{X}}$
around
$f:{\mathcal{W}}\rightarrow {\mathcal{X}}$
around
![]() $x$
.
$x$
.
2.2 Local VGIT chambers
Let
![]() $G$
be a linearly reductive group scheme over an algebraically closed field
$G$
be a linearly reductive group scheme over an algebraically closed field
![]() $k$
. Let
$k$
. Let
![]() $X$
be a
$X$
be a
![]() $k$
-scheme with an action of
$k$
-scheme with an action of
![]() $G$
via
$G$
via
 $\unicode[STIX]{x1D70E}:G\times X\rightarrow X$
. Let
$\unicode[STIX]{x1D70E}:G\times X\rightarrow X$
. Let
 $\unicode[STIX]{x1D712}:G\rightarrow \mathbb{G}_{m}=\operatorname{Spec}k[t]_{t}$
be a character. Set
$\unicode[STIX]{x1D712}:G\rightarrow \mathbb{G}_{m}=\operatorname{Spec}k[t]_{t}$
be a character. Set
 $A_{n}:=\{f\in A\mid \unicode[STIX]{x1D70E}^{\ast }(f)=\unicode[STIX]{x1D712}^{\ast }(t)^{-n}f\}$
. We define the VGIT ideals with respect to
$A_{n}:=\{f\in A\mid \unicode[STIX]{x1D70E}^{\ast }(f)=\unicode[STIX]{x1D712}^{\ast }(t)^{-n}f\}$
. We define the VGIT ideals with respect to
![]() $\unicode[STIX]{x1D712}$
to be
$\unicode[STIX]{x1D712}$
to be
 $$\begin{eqnarray}\displaystyle & \displaystyle I_{\unicode[STIX]{x1D712}}^{+}:=(f\in A\mid f\in A_{n}\text{ for some }n>0), & \displaystyle \nonumber\\ \displaystyle & \displaystyle I_{\unicode[STIX]{x1D712}}^{-}:=(f\in A\mid f\in A_{n}\text{ for some }n<0). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle I_{\unicode[STIX]{x1D712}}^{+}:=(f\in A\mid f\in A_{n}\text{ for some }n>0), & \displaystyle \nonumber\\ \displaystyle & \displaystyle I_{\unicode[STIX]{x1D712}}^{-}:=(f\in A\mid f\in A_{n}\text{ for some }n<0). & \displaystyle \nonumber\end{eqnarray}$$
The VGIT
![]() $(+)$
-chamber and
$(+)$
-chamber and
![]() $(-)$
-chamber of
$(-)$
-chamber of
![]() $X$
with respect to
$X$
with respect to
![]() $\unicode[STIX]{x1D712}$
are the open subschemes
$\unicode[STIX]{x1D712}$
are the open subschemes
 $$\begin{eqnarray}X_{\unicode[STIX]{x1D712}}^{+}:=X\setminus \mathbb{V}(I_{\unicode[STIX]{x1D712}}^{+}){\hookrightarrow}X,\quad X_{\unicode[STIX]{x1D712}}^{-}:=X\setminus \mathbb{V}(I_{\unicode[STIX]{x1D712}}^{-}){\hookrightarrow}X\end{eqnarray}$$
$$\begin{eqnarray}X_{\unicode[STIX]{x1D712}}^{+}:=X\setminus \mathbb{V}(I_{\unicode[STIX]{x1D712}}^{+}){\hookrightarrow}X,\quad X_{\unicode[STIX]{x1D712}}^{-}:=X\setminus \mathbb{V}(I_{\unicode[STIX]{x1D712}}^{-}){\hookrightarrow}X\end{eqnarray}$$
and, since the open subschemes
![]() $X_{\unicode[STIX]{x1D712}}^{+}$
,
$X_{\unicode[STIX]{x1D712}}^{+}$
,
![]() $X_{\unicode[STIX]{x1D712}}^{-}$
are
$X_{\unicode[STIX]{x1D712}}^{-}$
are
![]() $G$
-invariant, we also have stack-theoretic open immersions
$G$
-invariant, we also have stack-theoretic open immersions
 $$\begin{eqnarray}[X_{\unicode[STIX]{x1D712}}^{+}/G]{\hookrightarrow}[X/G]{\hookleftarrow}[X_{\unicode[STIX]{x1D712}}^{-}/G].\end{eqnarray}$$
$$\begin{eqnarray}[X_{\unicode[STIX]{x1D712}}^{+}/G]{\hookrightarrow}[X/G]{\hookleftarrow}[X_{\unicode[STIX]{x1D712}}^{-}/G].\end{eqnarray}$$
We will refer to these open immersions as the VGIT
 $(+)/(-)$
-chambers of
$(+)/(-)$
-chambers of
![]() $[X/G]$
with respect to
$[X/G]$
with respect to
![]() $\unicode[STIX]{x1D712}$
.
$\unicode[STIX]{x1D712}$
.
Finally, given the data of an algebraic stack
![]() ${\mathcal{X}}$
and a line bundle
${\mathcal{X}}$
and a line bundle
![]() ${\mathcal{L}}$
on
${\mathcal{L}}$
on
![]() ${\mathcal{X}}$
, we can define the VGIT chambers of a local quotient presentation. In this situation, note that if
${\mathcal{X}}$
, we can define the VGIT chambers of a local quotient presentation. In this situation, note that if
 $x\in {\mathcal{X}}(k)$
is any point, then there is a natural action of the automorphism group
$x\in {\mathcal{X}}(k)$
is any point, then there is a natural action of the automorphism group
![]() $G_{x}$
on the fiber
$G_{x}$
on the fiber
![]() ${\mathcal{L}}|_{BG_{x}}$
that induces a character
${\mathcal{L}}|_{BG_{x}}$
that induces a character
 $\unicode[STIX]{x1D712}_{{\mathcal{L}}}:G_{x}\rightarrow \mathbb{G}_{m}$
.
$\unicode[STIX]{x1D712}_{{\mathcal{L}}}:G_{x}\rightarrow \mathbb{G}_{m}$
.
Definition 2.4 (VGIT chambers of a local quotient presentation).
Let
![]() ${\mathcal{X}}$
be an algebraic stack of finite type over an algebraically closed field
${\mathcal{X}}$
be an algebraic stack of finite type over an algebraically closed field
![]() $k$
. Let
$k$
. Let
![]() ${\mathcal{L}}$
be a line bundle on
${\mathcal{L}}$
be a line bundle on
![]() ${\mathcal{X}}$
. Let
${\mathcal{X}}$
. Let
![]() $x\in {\mathcal{X}}$
be a closed point. If
$x\in {\mathcal{X}}$
be a closed point. If
 $f:{\mathcal{W}}\rightarrow {\mathcal{X}}$
is a local quotient presentation around
$f:{\mathcal{W}}\rightarrow {\mathcal{X}}$
is a local quotient presentation around
![]() $x$
, we define the chambers of
$x$
, we define the chambers of
![]() ${\mathcal{W}}$
with respect to
${\mathcal{W}}$
with respect to
![]() ${\mathcal{L}}$
to be the VGIT
${\mathcal{L}}$
to be the VGIT
 $(+)/(-)$
-chambers
$(+)/(-)$
-chambers
 $$\begin{eqnarray}{\mathcal{W}}_{{\mathcal{L}}}^{+}{\hookrightarrow}{\mathcal{W}}{\hookleftarrow}{\mathcal{W}}_{{\mathcal{L}}}^{-}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{W}}_{{\mathcal{L}}}^{+}{\hookrightarrow}{\mathcal{W}}{\hookleftarrow}{\mathcal{W}}_{{\mathcal{L}}}^{-}\end{eqnarray}$$
of
![]() ${\mathcal{W}}$
with respect to the character
${\mathcal{W}}$
with respect to the character
 $\unicode[STIX]{x1D712}_{{\mathcal{L}}}:G_{x}\rightarrow \mathbb{G}_{m}$
.
$\unicode[STIX]{x1D712}_{{\mathcal{L}}}:G_{x}\rightarrow \mathbb{G}_{m}$
.
2.3 Strongly étale morphisms
Definition 2.5. Let
 $f:{\mathcal{X}}\rightarrow {\mathcal{Y}}$
be a morphism of algebraic stacks of finite type over an algebraically closed field
$f:{\mathcal{X}}\rightarrow {\mathcal{Y}}$
be a morphism of algebraic stacks of finite type over an algebraically closed field
![]() $k$
. Assume that
$k$
. Assume that
![]() ${\mathcal{X}}$
and
${\mathcal{X}}$
and
![]() ${\mathcal{Y}}$
have affine diagonal. We say that:
${\mathcal{Y}}$
have affine diagonal. We say that:
-
– the morphism
 $f$
sends closed points to closed points if for every closed point
$f$
sends closed points to closed points if for every closed point
 $x\in {\mathcal{X}}$
, the point
$x\in {\mathcal{X}}$
, the point
 $f(x)\in {\mathcal{Y}}$
is closed;
$f(x)\in {\mathcal{Y}}$
is closed; -
– the morphism
 $f$
is stabilizer preserving at
$f$
is stabilizer preserving at
 $x\in {\mathcal{X}}(k)$
if
$x\in {\mathcal{X}}(k)$
if
 $\operatorname{Aut}_{{\mathcal{X}}(k)}(x)\rightarrow \operatorname{Aut}_{{\mathcal{Y}}(k)}(f(x))$
is an isomorphism;
$\operatorname{Aut}_{{\mathcal{X}}(k)}(x)\rightarrow \operatorname{Aut}_{{\mathcal{Y}}(k)}(f(x))$
is an isomorphism; -
– for a closed point
 $x\in {\mathcal{X}}$
, the morphism
$x\in {\mathcal{X}}$
, the morphism
 $f$
is strongly étale at
$f$
is strongly étale at
 $x$
if
$x$
if
 $f$
is étale at
$f$
is étale at
 $x$
,
$x$
,
 $f$
is stabilizer preserving at
$f$
is stabilizer preserving at
 $x$
, and
$x$
, and
 $f(x)\in {\mathcal{Y}}$
is closed;
$f(x)\in {\mathcal{Y}}$
is closed; -
– the morphism
 $f$
is strongly étale if
$f$
is strongly étale if
 $f$
is strongly étale at all closed points of
$f$
is strongly étale at all closed points of
 ${\mathcal{X}}$
.
${\mathcal{X}}$
.
Definition 2.6. Let
 $\unicode[STIX]{x1D719}:{\mathcal{X}}\rightarrow X$
be a good moduli space. We say that an open substack
$\unicode[STIX]{x1D719}:{\mathcal{X}}\rightarrow X$
be a good moduli space. We say that an open substack
![]() ${\mathcal{U}}\subset {\mathcal{X}}$
is saturated if
${\mathcal{U}}\subset {\mathcal{X}}$
is saturated if
 $\unicode[STIX]{x1D719}^{-1}(\unicode[STIX]{x1D719}({\mathcal{U}}))={\mathcal{U}}$
.
$\unicode[STIX]{x1D719}^{-1}(\unicode[STIX]{x1D719}({\mathcal{U}}))={\mathcal{U}}$
.
The following proposition is simply a stack-theoretic formulation of Luna’s well-known results in invariant theory [Reference LunaLun73, Chapitre II] often referred to as Luna’s fundamental lemma. It justifies the terminology strongly étale by showing that strongly étale morphisms induce étale morphisms of good moduli spaces. It also shows that for a morphism of algebraic stacks admitting good moduli spaces, strong étaleness is an open condition.
Proposition 2.7. Let
![]() ${\mathcal{W}}$
and
${\mathcal{W}}$
and
![]() ${\mathcal{X}}$
be algebraic stacks of finite type over an algebraically closed field
${\mathcal{X}}$
be algebraic stacks of finite type over an algebraically closed field
![]() $k$
. Assume that
$k$
. Assume that
![]() ${\mathcal{W}}$
and
${\mathcal{W}}$
and
![]() ${\mathcal{X}}$
have affine diagonal. Consider a commutative diagram
${\mathcal{X}}$
have affine diagonal. Consider a commutative diagram

where
![]() $f$
is representable and separated, and both
$f$
is representable and separated, and both
![]() $\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D711}$
and
![]() $\unicode[STIX]{x1D719}$
are good moduli spaces. Then:
$\unicode[STIX]{x1D719}$
are good moduli spaces. Then:
-
(i) if
 $f$
is strongly étale at
$f$
is strongly étale at
 $w\in {\mathcal{W}}$
, then
$w\in {\mathcal{W}}$
, then
 $g$
is étale at
$g$
is étale at
 $\unicode[STIX]{x1D711}(w)$
;
$\unicode[STIX]{x1D711}(w)$
; -
(ii) if
 $f$
is strongly étale, then
$f$
is strongly étale, then
 $g$
is étale and Diagram (2.1) is Cartesian; and
$g$
is étale and Diagram (2.1) is Cartesian; and -
(iii) there exists a saturated open substack
 ${\mathcal{U}}\subset {\mathcal{W}}$
such that:
${\mathcal{U}}\subset {\mathcal{W}}$
such that:-
(a) the morphism
 $f|_{{\mathcal{U}}}:{\mathcal{U}}\rightarrow {\mathcal{X}}$
is strongly étale and
$f|_{{\mathcal{U}}}:{\mathcal{U}}\rightarrow {\mathcal{X}}$
is strongly étale and
 $f({\mathcal{U}})\subset {\mathcal{X}}$
is saturated; and
$f({\mathcal{U}})\subset {\mathcal{X}}$
is saturated; and -
(b) if
 $w\in {\mathcal{W}}$
is a closed point such that
$w\in {\mathcal{W}}$
is a closed point such that
 $f$
is strongly étale at
$f$
is strongly étale at
 $w$
, then
$w$
, then
 $w\in {\mathcal{U}}$
.
$w\in {\mathcal{U}}$
.
-
Proof. Alper [Reference AlperAlp13, Theorem 5.1] gives part (i) and that
![]() $g$
is étale in (ii). The hypotheses in (ii) imply that the induced morphism
$g$
is étale in (ii). The hypotheses in (ii) imply that the induced morphism
 $\unicode[STIX]{x1D6F9}:{\mathcal{W}}\rightarrow W\times _{X}{\mathcal{X}}$
is representable, separated, quasi-finite, and sends closed points to closed points. Alper [Reference AlperAlp13, Proposition 6.4] implies that
$\unicode[STIX]{x1D6F9}:{\mathcal{W}}\rightarrow W\times _{X}{\mathcal{X}}$
is representable, separated, quasi-finite, and sends closed points to closed points. Alper [Reference AlperAlp13, Proposition 6.4] implies that
![]() $\unicode[STIX]{x1D6F9}$
is finite. Moreover, since
$\unicode[STIX]{x1D6F9}$
is finite. Moreover, since
![]() $f$
and
$f$
and
![]() $g$
are étale, so is
$g$
are étale, so is
![]() $\unicode[STIX]{x1D6F9}$
. But since
$\unicode[STIX]{x1D6F9}$
. But since
![]() ${\mathcal{W}}$
and
${\mathcal{W}}$
and
 $W\times _{X}{\mathcal{X}}$
both have
$W\times _{X}{\mathcal{X}}$
both have
![]() $W$
as a good moduli space, it follows that a closed point in
$W$
as a good moduli space, it follows that a closed point in
 $W\times _{X}{\mathcal{X}}$
has a unique preimage under
$W\times _{X}{\mathcal{X}}$
has a unique preimage under
![]() $\unicode[STIX]{x1D6F9}$
. Therefore,
$\unicode[STIX]{x1D6F9}$
. Therefore,
![]() $\unicode[STIX]{x1D6F9}$
is an isomorphism and the diagram is Cartesian. Statement (iii) follows from [Reference AlperAlp10, Theorem 6.10].◻
$\unicode[STIX]{x1D6F9}$
is an isomorphism and the diagram is Cartesian. Statement (iii) follows from [Reference AlperAlp10, Theorem 6.10].◻
Lemma 2.8. Let
![]() ${\mathcal{X}}$
be an algebraic stack of finite type over an algebraically closed field
${\mathcal{X}}$
be an algebraic stack of finite type over an algebraically closed field
![]() $k$
. Suppose that
$k$
. Suppose that
![]() ${\mathcal{X}}$
has affine diagonal and that there exists a good moduli space
${\mathcal{X}}$
has affine diagonal and that there exists a good moduli space
 $\unicode[STIX]{x1D719}:{\mathcal{X}}\rightarrow X$
. Let
$\unicode[STIX]{x1D719}:{\mathcal{X}}\rightarrow X$
. Let
![]() $x\in {\mathcal{X}}$
be a closed point and
$x\in {\mathcal{X}}$
be a closed point and
![]() ${\mathcal{U}}\subset {\mathcal{X}}$
be an open substack containing
${\mathcal{U}}\subset {\mathcal{X}}$
be an open substack containing
![]() $x$
. Then there exists a saturated open substack
$x$
. Then there exists a saturated open substack
![]() ${\mathcal{U}}_{1}\subset {\mathcal{U}}$
containing
${\mathcal{U}}_{1}\subset {\mathcal{U}}$
containing
![]() $x$
. Moreover, if
$x$
. Moreover, if
 ${\mathcal{X}}\simeq [\operatorname{Spec}A/G]$
with
${\mathcal{X}}\simeq [\operatorname{Spec}A/G]$
with
![]() $G$
linearly reductive, then
$G$
linearly reductive, then
![]() ${\mathcal{U}}_{1}$
can be chosen to be of the form
${\mathcal{U}}_{1}$
can be chosen to be of the form
 $[\operatorname{Spec}B/G]$
for a
$[\operatorname{Spec}B/G]$
for a
![]() $G$
-invariant open affine subscheme
$G$
-invariant open affine subscheme
 $\operatorname{Spec}B\subset \operatorname{Spec}A$
.
$\operatorname{Spec}B\subset \operatorname{Spec}A$
.
Proof. The substacks
![]() $\{x\}$
and
$\{x\}$
and
![]() ${\mathcal{X}}\setminus {\mathcal{U}}$
are closed and disjoint. By [Reference AlperAlp13, Theorem 4.16],
${\mathcal{X}}\setminus {\mathcal{U}}$
are closed and disjoint. By [Reference AlperAlp13, Theorem 4.16],
![]() $\unicode[STIX]{x1D719}(\{x\})$
and
$\unicode[STIX]{x1D719}(\{x\})$
and
 $Z:=\unicode[STIX]{x1D719}({\mathcal{X}}\setminus {\mathcal{U}})$
are closed and disjoint. For the first statement, take
$Z:=\unicode[STIX]{x1D719}({\mathcal{X}}\setminus {\mathcal{U}})$
are closed and disjoint. For the first statement, take
 ${\mathcal{U}}_{1}=\unicode[STIX]{x1D719}^{-1}(X\setminus Z)$
. For the second statement, take
${\mathcal{U}}_{1}=\unicode[STIX]{x1D719}^{-1}(X\setminus Z)$
. For the second statement, take
 ${\mathcal{U}}_{1}=\unicode[STIX]{x1D719}^{-1}(U_{1})$
for an affine open subscheme
${\mathcal{U}}_{1}=\unicode[STIX]{x1D719}^{-1}(U_{1})$
for an affine open subscheme
 $U_{1}\subset X\setminus Z$
.◻
$U_{1}\subset X\setminus Z$
.◻
Lemma 2.9. Let
![]() ${\mathcal{X}}$
and
${\mathcal{X}}$
and
![]() ${\mathcal{Y}}$
be algebraic stacks of finite type over an algebraically closed field
${\mathcal{Y}}$
be algebraic stacks of finite type over an algebraically closed field
![]() $k$
. Suppose that
$k$
. Suppose that
![]() ${\mathcal{X}}$
and
${\mathcal{X}}$
and
![]() ${\mathcal{Y}}$
have affine diagonal. Let
${\mathcal{Y}}$
have affine diagonal. Let
 $f:{\mathcal{X}}\rightarrow {\mathcal{Y}}$
be a strongly étale morphism. Suppose that for points
$f:{\mathcal{X}}\rightarrow {\mathcal{Y}}$
be a strongly étale morphism. Suppose that for points
 $x\in {\mathcal{X}}(k)$
and
$x\in {\mathcal{X}}(k)$
and
 $y\in {\mathcal{Y}}(k)$
, the closed substacks
$y\in {\mathcal{Y}}(k)$
, the closed substacks
 $\overline{\{x\}}\subset {\mathcal{X}}$
and
$\overline{\{x\}}\subset {\mathcal{X}}$
and
 $\overline{\{y\}}\subset {\mathcal{Y}}$
admit good moduli spaces. Then, for any morphism of finite type
$\overline{\{y\}}\subset {\mathcal{Y}}$
admit good moduli spaces. Then, for any morphism of finite type
 $g:{\mathcal{Y}}^{\prime }\rightarrow {\mathcal{Y}}$
with affine diagonal, the base change
$g:{\mathcal{Y}}^{\prime }\rightarrow {\mathcal{Y}}$
with affine diagonal, the base change
 $f^{\prime }:{\mathcal{X}}\times _{{\mathcal{Y}}}{\mathcal{Y}}^{\prime }\rightarrow {\mathcal{Y}}^{\prime }$
is strongly étale.
$f^{\prime }:{\mathcal{X}}\times _{{\mathcal{Y}}}{\mathcal{Y}}^{\prime }\rightarrow {\mathcal{Y}}^{\prime }$
is strongly étale.
Proof. Clearly, the morphism
![]() $f^{\prime }$
is étale. Let
$f^{\prime }$
is étale. Let
 $x^{\prime }\in {\mathcal{X}}\times _{{\mathcal{Y}}}{\mathcal{Y}}^{\prime }$
be a closed point. To check that
$x^{\prime }\in {\mathcal{X}}\times _{{\mathcal{Y}}}{\mathcal{Y}}^{\prime }$
be a closed point. To check that
![]() $f^{\prime }$
is stabilizer preserving at
$f^{\prime }$
is stabilizer preserving at
![]() $x^{\prime }$
and
$x^{\prime }$
and
 $f^{\prime }(x^{\prime })\in {\mathcal{Y}}^{\prime }$
is closed, we may replace
$f^{\prime }(x^{\prime })\in {\mathcal{Y}}^{\prime }$
is closed, we may replace
![]() ${\mathcal{Y}}$
with
${\mathcal{Y}}$
with
 $\overline{\{g(f^{\prime }(x^{\prime }))\}}$
and
$\overline{\{g(f^{\prime }(x^{\prime }))\}}$
and
![]() ${\mathcal{X}}$
with
${\mathcal{X}}$
with
 $\overline{\{g^{\prime }(x^{\prime })\}}$
, where
$\overline{\{g^{\prime }(x^{\prime })\}}$
, where
 $g^{\prime }:{\mathcal{X}}\times _{{\mathcal{Y}}}{\mathcal{Y}}^{\prime }\rightarrow {\mathcal{X}}$
. Since
$g^{\prime }:{\mathcal{X}}\times _{{\mathcal{Y}}}{\mathcal{Y}}^{\prime }\rightarrow {\mathcal{X}}$
. Since
![]() $f$
is strongly étale, Proposition 2.7(ii) implies that
$f$
is strongly étale, Proposition 2.7(ii) implies that
![]() $f$
is in fact an isomorphism, and the desired properties of
$f$
is in fact an isomorphism, and the desired properties of
![]() $f^{\prime }$
are immediate.◻
$f^{\prime }$
are immediate.◻
3 General existence results
In this section, we prove Theorems 1.2 and 1.3 and Proposition 1.4.
3.1 Existence via local quotient presentations
Proposition 3.1. Let
![]() ${\mathcal{X}}$
be an algebraic stack of finite type over an algebraically closed field
${\mathcal{X}}$
be an algebraic stack of finite type over an algebraically closed field
![]() $k$
. Suppose that
$k$
. Suppose that
![]() ${\mathcal{X}}$
has affine diagonal. Suppose that:
${\mathcal{X}}$
has affine diagonal. Suppose that:
-
(i) there exists an affine, strongly étale, and surjective morphism
 $f:{\mathcal{X}}_{1}\rightarrow {\mathcal{X}}$
from an algebraic stack
$f:{\mathcal{X}}_{1}\rightarrow {\mathcal{X}}$
from an algebraic stack
 ${\mathcal{X}}_{1}$
admitting a good moduli space
${\mathcal{X}}_{1}$
admitting a good moduli space
 $\unicode[STIX]{x1D719}_{1}:{\mathcal{X}}_{1}\rightarrow X_{1}$
; and
$\unicode[STIX]{x1D719}_{1}:{\mathcal{X}}_{1}\rightarrow X_{1}$
; and -
(ii) for any point
 $x\in {\mathcal{X}}(k)$
, the closed substack
$x\in {\mathcal{X}}(k)$
, the closed substack
 $\overline{\{x\}}$
admits a good moduli space.
$\overline{\{x\}}$
admits a good moduli space.
Then
![]() ${\mathcal{X}}$
admits a good moduli space
${\mathcal{X}}$
admits a good moduli space
 $\unicode[STIX]{x1D719}:{\mathcal{X}}\rightarrow X$
.
$\unicode[STIX]{x1D719}:{\mathcal{X}}\rightarrow X$
.
Proof. Set
 ${\mathcal{X}}_{2}={\mathcal{X}}_{1}\times _{{\mathcal{X}}}{\mathcal{X}}_{1}$
. By Lemma 2.9, the projections
${\mathcal{X}}_{2}={\mathcal{X}}_{1}\times _{{\mathcal{X}}}{\mathcal{X}}_{1}$
. By Lemma 2.9, the projections
 $p_{1},p_{2}:{\mathcal{X}}_{2}\rightarrow {\mathcal{X}}_{1}$
are strongly étale. As
$p_{1},p_{2}:{\mathcal{X}}_{2}\rightarrow {\mathcal{X}}_{1}$
are strongly étale. As
![]() $f$
is affine, there exists a good moduli space
$f$
is affine, there exists a good moduli space
 $\unicode[STIX]{x1D719}_{2}:{\mathcal{X}}_{2}\rightarrow X_{2}$
with projections
$\unicode[STIX]{x1D719}_{2}:{\mathcal{X}}_{2}\rightarrow X_{2}$
with projections
 $q_{1},q_{2}:X_{2}\rightarrow X_{1}$
. Similarly, the algebraic stack
$q_{1},q_{2}:X_{2}\rightarrow X_{1}$
. Similarly, the algebraic stack
 ${\mathcal{X}}_{3}:={\mathcal{X}}_{1}\times _{{\mathcal{X}}}{\mathcal{X}}_{1}\times _{{\mathcal{X}}}{\mathcal{X}}_{1}$
admits a good moduli space
${\mathcal{X}}_{3}:={\mathcal{X}}_{1}\times _{{\mathcal{X}}}{\mathcal{X}}_{1}\times _{{\mathcal{X}}}{\mathcal{X}}_{1}$
admits a good moduli space
 $\unicode[STIX]{x1D719}_{3}:{\mathcal{X}}_{3}\rightarrow X_{3}$
and the three projections
$\unicode[STIX]{x1D719}_{3}:{\mathcal{X}}_{3}\rightarrow X_{3}$
and the three projections
 ${\mathcal{X}}_{3}\rightarrow {\mathcal{X}}_{2}$
are strongly étale. By Proposition 2.7(ii), the induced diagram
${\mathcal{X}}_{3}\rightarrow {\mathcal{X}}_{2}$
are strongly étale. By Proposition 2.7(ii), the induced diagram

is Cartesian. Moreover, by the universality of good moduli spaces, there are an induced identity map
 $X_{1}\rightarrow X_{2}$
, an inverse
$X_{1}\rightarrow X_{2}$
, an inverse
 $X_{2}\rightarrow X_{2}$
, and a composition
$X_{2}\rightarrow X_{2}$
, and a composition
 $X_{2}\times _{q_{1},X_{1},q_{2}}X_{2}\rightarrow X_{2}$
giving
$X_{2}\times _{q_{1},X_{1},q_{2}}X_{2}\rightarrow X_{2}$
giving
 $X_{2}\rightrightarrows X_{1}$
an étale groupoid structure.
$X_{2}\rightrightarrows X_{1}$
an étale groupoid structure.
To check that
 $(q_{1},q_{2}):X_{2}\rightarrow X_{1}\times X_{1}$
is a monomorphism, it suffices to check that there is a unique preimage of
$(q_{1},q_{2}):X_{2}\rightarrow X_{1}\times X_{1}$
is a monomorphism, it suffices to check that there is a unique preimage of
 $(x_{1},x_{1})\in X_{1}\times X_{1}$
, where
$(x_{1},x_{1})\in X_{1}\times X_{1}$
, where
 $x_{1}\in X_{1}(k)$
. Let
$x_{1}\in X_{1}(k)$
. Let
![]() $\unicode[STIX]{x1D709}_{1}\in {\mathcal{X}}_{1}$
be the unique closed point in
$\unicode[STIX]{x1D709}_{1}\in {\mathcal{X}}_{1}$
be the unique closed point in
 $\unicode[STIX]{x1D719}_{1}^{-1}(x_{1})$
. Since
$\unicode[STIX]{x1D719}_{1}^{-1}(x_{1})$
. Since
 ${\mathcal{X}}_{1}\rightarrow {\mathcal{X}}$
is stabilizer preserving at
${\mathcal{X}}_{1}\rightarrow {\mathcal{X}}$
is stabilizer preserving at
![]() $\unicode[STIX]{x1D709}_{1}$
, we can set
$\unicode[STIX]{x1D709}_{1}$
, we can set
 $G:=\operatorname{Aut}_{{\mathcal{X}}_{1}(k)}(\unicode[STIX]{x1D709}_{1})\simeq \operatorname{Aut}_{{\mathcal{X}}(k)}(f(\unicode[STIX]{x1D709}_{1}))$
. There are diagrams
$G:=\operatorname{Aut}_{{\mathcal{X}}_{1}(k)}(\unicode[STIX]{x1D709}_{1})\simeq \operatorname{Aut}_{{\mathcal{X}}(k)}(f(\unicode[STIX]{x1D709}_{1}))$
. There are diagrams

where the squares in the left-hand diagram are Cartesian. Suppose that
 $x_{2}\in X_{2}(k)$
is a preimage of
$x_{2}\in X_{2}(k)$
is a preimage of
![]() $(x_{1},x_{1})$
under
$(x_{1},x_{1})$
under
 $X_{2}\rightarrow X_{1}\times X_{1}$
. Let
$X_{2}\rightarrow X_{1}\times X_{1}$
. Let
![]() $\unicode[STIX]{x1D709}_{2}\in {\mathcal{X}}_{2}$
be the unique closed point in
$\unicode[STIX]{x1D709}_{2}\in {\mathcal{X}}_{2}$
be the unique closed point in
 $\unicode[STIX]{x1D719}_{2}^{-1}(x_{2})$
. Then
$\unicode[STIX]{x1D719}_{2}^{-1}(x_{2})$
. Then
 $(p_{1}(\unicode[STIX]{x1D709}_{2}),p_{2}(\unicode[STIX]{x1D709}_{2}))\in {\mathcal{X}}_{1}\times {\mathcal{X}}_{1}$
is closed and is therefore the unique closed point
$(p_{1}(\unicode[STIX]{x1D709}_{2}),p_{2}(\unicode[STIX]{x1D709}_{2}))\in {\mathcal{X}}_{1}\times {\mathcal{X}}_{1}$
is closed and is therefore the unique closed point
![]() $(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{1})$
in
$(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{1})$
in
 $(\unicode[STIX]{x1D719}_{1}\times \unicode[STIX]{x1D719}_{1})^{-1}(x_{1},x_{1})$
. But, by Cartesianness of the left-hand diagram, the point
$(\unicode[STIX]{x1D719}_{1}\times \unicode[STIX]{x1D719}_{1})^{-1}(x_{1},x_{1})$
. But, by Cartesianness of the left-hand diagram, the point
![]() $\unicode[STIX]{x1D709}_{2}$
is the unique preimage of
$\unicode[STIX]{x1D709}_{2}$
is the unique preimage of
![]() $(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{1})$
under
$(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{1})$
under
 ${\mathcal{X}}_{2}\rightarrow {\mathcal{X}}_{1}\times {\mathcal{X}}_{1}$
. It follows that the point
${\mathcal{X}}_{2}\rightarrow {\mathcal{X}}_{1}\times {\mathcal{X}}_{1}$
. It follows that the point
![]() $x_{2}$
is the unique preimage of
$x_{2}$
is the unique preimage of
![]() $(x_{1},x_{1})$
.
$(x_{1},x_{1})$
.
Since
 $X_{2}\times _{q_{1},X_{1},q_{2}}X_{2}\rightarrow X_{2}$
is an étale equivalence relation, there exist an algebraic space quotient
$X_{2}\times _{q_{1},X_{1},q_{2}}X_{2}\rightarrow X_{2}$
is an étale equivalence relation, there exist an algebraic space quotient
![]() $X$
and induced maps
$X$
and induced maps
 $\unicode[STIX]{x1D719}:{\mathcal{X}}\rightarrow X$
and
$\unicode[STIX]{x1D719}:{\mathcal{X}}\rightarrow X$
and
 $X_{1}\rightarrow X$
. Consider
$X_{1}\rightarrow X$
. Consider

Since
 ${\mathcal{X}}_{2}\simeq {\mathcal{X}}_{1}\times _{X_{1}}X_{2}$
and
${\mathcal{X}}_{2}\simeq {\mathcal{X}}_{1}\times _{X_{1}}X_{2}$
and
 $X_{2}\simeq X_{1}\times _{X}X_{1}$
, the left-hand and outer squares above are Cartesian. Since
$X_{2}\simeq X_{1}\times _{X}X_{1}$
, the left-hand and outer squares above are Cartesian. Since
 ${\mathcal{X}}_{1}\rightarrow {\mathcal{X}}$
is étale and surjective, it follows that the right-hand square is Cartesian. By descent [Reference AlperAlp13, Proposition 4.7],
${\mathcal{X}}_{1}\rightarrow {\mathcal{X}}$
is étale and surjective, it follows that the right-hand square is Cartesian. By descent [Reference AlperAlp13, Proposition 4.7],
 $\unicode[STIX]{x1D719}:{\mathcal{X}}\rightarrow X$
is a good moduli space.◻
$\unicode[STIX]{x1D719}:{\mathcal{X}}\rightarrow X$
is a good moduli space.◻
Proof of Theorem 1.2.
After taking a disjoint union of finitely many local quotient presentations, there exists a strongly étale, affine, and surjective morphism
 $f:{\mathcal{W}}\rightarrow {\mathcal{X}}$
, where
$f:{\mathcal{W}}\rightarrow {\mathcal{X}}$
, where
![]() ${\mathcal{W}}$
admits a good moduli space. The theorem now follows from Proposition 3.1.◻
${\mathcal{W}}$
admits a good moduli space. The theorem now follows from Proposition 3.1.◻
3.2 Existence via local VGIT
To prove Theorem 1.3, we will need some preliminary lemmas.
Lemma 3.2. Let
![]() $G$
be a linearly reductive group scheme over an algebraically closed field
$G$
be a linearly reductive group scheme over an algebraically closed field
![]() $k$
acting on an affine scheme
$k$
acting on an affine scheme
![]() $X$
of finite type over
$X$
of finite type over
![]() $k$
. Let
$k$
. Let
 $\unicode[STIX]{x1D712}:G\rightarrow \mathbb{G}_{m}$
be a non-trivial character. Let
$\unicode[STIX]{x1D712}:G\rightarrow \mathbb{G}_{m}$
be a non-trivial character. Let
 $\unicode[STIX]{x1D706}:\mathbb{G}_{m}\rightarrow G$
be a one-parameter subgroup and
$\unicode[STIX]{x1D706}:\mathbb{G}_{m}\rightarrow G$
be a one-parameter subgroup and
 $x\in X_{\unicode[STIX]{x1D712}}^{-}(k)$
such that
$x\in X_{\unicode[STIX]{x1D712}}^{-}(k)$
such that
 $x_{0}=\lim _{t\rightarrow 0}\unicode[STIX]{x1D706}(t)\cdot x\in X^{G}$
is fixed by
$x_{0}=\lim _{t\rightarrow 0}\unicode[STIX]{x1D706}(t)\cdot x\in X^{G}$
is fixed by
![]() $G$
. Then
$G$
. Then
 $\langle \unicode[STIX]{x1D712},\unicode[STIX]{x1D706}\rangle >0$
.
$\langle \unicode[STIX]{x1D712},\unicode[STIX]{x1D706}\rangle >0$
.
Proof. As
 $x\in X_{\unicode[STIX]{x1D712}}^{-}$
, we have
$x\in X_{\unicode[STIX]{x1D712}}^{-}$
, we have
 $\langle \unicode[STIX]{x1D712},\unicode[STIX]{x1D706}\rangle \geqslant 0$
by the Hilbert–Mumford criterion (cf. [Reference Alper, Fedorchuk, Smyth and van der WyckAFSvdW17, Proposition 3.5]). Suppose that
$\langle \unicode[STIX]{x1D712},\unicode[STIX]{x1D706}\rangle \geqslant 0$
by the Hilbert–Mumford criterion (cf. [Reference Alper, Fedorchuk, Smyth and van der WyckAFSvdW17, Proposition 3.5]). Suppose that
 $\langle \unicode[STIX]{x1D712},\unicode[STIX]{x1D706}\rangle =0$
. Considering the action of
$\langle \unicode[STIX]{x1D712},\unicode[STIX]{x1D706}\rangle =0$
. Considering the action of
![]() $G$
on
$G$
on
![]() $X\times \mathbb{A}^{1}$
induced by
$X\times \mathbb{A}^{1}$
induced by
![]() $\unicode[STIX]{x1D712}^{-1}$
via
$\unicode[STIX]{x1D712}^{-1}$
via
 $g\cdot (x,s)=(g\cdot x,\unicode[STIX]{x1D712}(g)^{-1}s)$
, we obtain
$g\cdot (x,s)=(g\cdot x,\unicode[STIX]{x1D712}(g)^{-1}s)$
, we obtain
 $$\begin{eqnarray}\lim _{t\rightarrow 0}\unicode[STIX]{x1D706}(t)\cdot (x,1)=(x_{0},1)\in X^{G}\times \mathbb{A}^{1}.\end{eqnarray}$$
$$\begin{eqnarray}\lim _{t\rightarrow 0}\unicode[STIX]{x1D706}(t)\cdot (x,1)=(x_{0},1)\in X^{G}\times \mathbb{A}^{1}.\end{eqnarray}$$
But
![]() $X^{G}$
is contained in the unstable locus
$X^{G}$
is contained in the unstable locus
![]() $X\setminus X_{\unicode[STIX]{x1D712}}^{-}$
since
$X\setminus X_{\unicode[STIX]{x1D712}}^{-}$
since
![]() $\unicode[STIX]{x1D712}$
is a non-trivial linearization. It follows that
$\unicode[STIX]{x1D712}$
is a non-trivial linearization. It follows that
 $\overline{G\cdot (x,1)}\cap (X^{G}\times \{0\})\neq \emptyset$
, which contradicts
$\overline{G\cdot (x,1)}\cap (X^{G}\times \{0\})\neq \emptyset$
, which contradicts
 $x\in X_{\unicode[STIX]{x1D712}}^{-}$
(cf. [Reference Alper, Fedorchuk, Smyth and van der WyckAFSvdW17, Remark 3.2]).◻
$x\in X_{\unicode[STIX]{x1D712}}^{-}$
(cf. [Reference Alper, Fedorchuk, Smyth and van der WyckAFSvdW17, Remark 3.2]).◻
Lemma 3.3 [Reference Alper, Fedorchuk, Smyth and van der WyckAFSvdW17, Lemma 3.9].
Let
![]() $G$
be a linearly reductive group scheme over an algebraically closed field
$G$
be a linearly reductive group scheme over an algebraically closed field
![]() $k$
and let
$k$
and let
 $\unicode[STIX]{x1D712}:G\rightarrow \mathbb{G}_{m}$
be a character. Let
$\unicode[STIX]{x1D712}:G\rightarrow \mathbb{G}_{m}$
be a character. Let
 $h:\operatorname{Spec}A=X\rightarrow Y=\operatorname{Spec}B$
be a
$h:\operatorname{Spec}A=X\rightarrow Y=\operatorname{Spec}B$
be a
![]() $G$
-invariant morphism of affine schemes of finite type over
$G$
-invariant morphism of affine schemes of finite type over
![]() $k$
. Assume that
$k$
. Assume that
 $A=B\otimes _{B^{G}}A^{G}$
. Then
$A=B\otimes _{B^{G}}A^{G}$
. Then
 $h^{-1}(Y_{\unicode[STIX]{x1D712}}^{+})=X_{\unicode[STIX]{x1D712}}^{+}$
and
$h^{-1}(Y_{\unicode[STIX]{x1D712}}^{+})=X_{\unicode[STIX]{x1D712}}^{+}$
and
 $h^{-1}(Y_{\unicode[STIX]{x1D712}}^{-})=X_{\unicode[STIX]{x1D712}}^{-}$
.
$h^{-1}(Y_{\unicode[STIX]{x1D712}}^{-})=X_{\unicode[STIX]{x1D712}}^{-}$
.
Remark 3.4. While [Reference Alper, Fedorchuk, Smyth and van der WyckAFSvdW17, Proposition 3.5 and Lemma 3.9] have an underlying characteristic-
![]() $0$
hypothesis, it is immediate that the proofs carry over to any characteristic.
$0$
hypothesis, it is immediate that the proofs carry over to any characteristic.
Lemma 3.5. Let
![]() ${\mathcal{X}}$
be an algebraic stack of finite type over an algebraically closed field
${\mathcal{X}}$
be an algebraic stack of finite type over an algebraically closed field
![]() $k$
and let
$k$
and let
![]() ${\mathcal{L}}$
be a line bundle on
${\mathcal{L}}$
be a line bundle on
![]() ${\mathcal{X}}$
. Let
${\mathcal{X}}$
. Let
 ${\mathcal{X}}^{+},{\mathcal{X}}^{-}\subset {\mathcal{X}}$
be open substacks and let
${\mathcal{X}}^{+},{\mathcal{X}}^{-}\subset {\mathcal{X}}$
be open substacks and let
 ${\mathcal{Z}}^{+}={\mathcal{X}}\smallsetminus {\mathcal{X}}^{+}$
,
${\mathcal{Z}}^{+}={\mathcal{X}}\smallsetminus {\mathcal{X}}^{+}$
,
 ${\mathcal{Z}}^{-}={\mathcal{X}}\smallsetminus {\mathcal{X}}^{-}$
be their reduced complements. Suppose that for all closed points
${\mathcal{Z}}^{-}={\mathcal{X}}\smallsetminus {\mathcal{X}}^{-}$
be their reduced complements. Suppose that for all closed points
![]() $x\in {\mathcal{X}}$
, there exist a local quotient presentation
$x\in {\mathcal{X}}$
, there exist a local quotient presentation
 $f:{\mathcal{W}}\rightarrow {\mathcal{X}}$
around
$f:{\mathcal{W}}\rightarrow {\mathcal{X}}$
around
![]() $x$
and a Cartesian diagram
$x$
and a Cartesian diagram

where
 ${\mathcal{W}}^{+}={\mathcal{W}}_{{\mathcal{L}}}^{+}$
and
${\mathcal{W}}^{+}={\mathcal{W}}_{{\mathcal{L}}}^{+}$
and
 ${\mathcal{W}}^{-}={\mathcal{W}}_{{\mathcal{L}}}^{-}$
are the VGIT chambers of
${\mathcal{W}}^{-}={\mathcal{W}}_{{\mathcal{L}}}^{-}$
are the VGIT chambers of
![]() ${\mathcal{W}}$
with respect to
${\mathcal{W}}$
with respect to
![]() ${\mathcal{L}}$
. Then:
${\mathcal{L}}$
. Then:
-
(i) if
 $z\in {\mathcal{X}}^{+}(k)\cap {\mathcal{X}}^{-}(k)$
, then the closure of
$z\in {\mathcal{X}}^{+}(k)\cap {\mathcal{X}}^{-}(k)$
, then the closure of
 $z$
in
$z$
in
 ${\mathcal{X}}$
is contained in
${\mathcal{X}}$
is contained in
 ${\mathcal{X}}^{+}\cap {\mathcal{X}}^{-}$
; and
${\mathcal{X}}^{+}\cap {\mathcal{X}}^{-}$
; and -
(ii) if
 $z\in {\mathcal{X}}(k)$
is a closed point, then either
$z\in {\mathcal{X}}(k)$
is a closed point, then either
 $z\in {\mathcal{X}}^{+}\cap {\mathcal{X}}^{-}$
or
$z\in {\mathcal{X}}^{+}\cap {\mathcal{X}}^{-}$
or
 $z\in {\mathcal{Z}}^{+}\cap {\mathcal{Z}}^{-}$
.
$z\in {\mathcal{Z}}^{+}\cap {\mathcal{Z}}^{-}$
.
Proof. For (i), if the closure of
![]() $z$
in
$z$
in
![]() ${\mathcal{X}}$
is not contained in
${\mathcal{X}}$
is not contained in
 ${\mathcal{X}}^{+}\cap {\mathcal{X}}^{-}$
, then there exists an isotrivial specialization
${\mathcal{X}}^{+}\cap {\mathcal{X}}^{-}$
, then there exists an isotrivial specialization
![]() $z{\rightsquigarrow}x$
to a closed point in
$z{\rightsquigarrow}x$
to a closed point in
 ${\mathcal{X}}\setminus ({\mathcal{X}}^{+}\cap {\mathcal{X}}^{-})$
. Choose a local quotient presentation
${\mathcal{X}}\setminus ({\mathcal{X}}^{+}\cap {\mathcal{X}}^{-})$
. Choose a local quotient presentation
 $f:{\mathcal{W}}=[W/G_{x}]\rightarrow {\mathcal{X}}$
around
$f:{\mathcal{W}}=[W/G_{x}]\rightarrow {\mathcal{X}}$
around
![]() $x$
such that (3.1) is Cartesian. Since
$x$
such that (3.1) is Cartesian. Since
 $f^{-1}(x)\not \subset {\mathcal{W}}^{+}\cap {\mathcal{W}}^{-}$
, the character
$f^{-1}(x)\not \subset {\mathcal{W}}^{+}\cap {\mathcal{W}}^{-}$
, the character
 $\unicode[STIX]{x1D712}={\mathcal{L}}|_{BG_{x}}$
is non-trivial. By the Hilbert–Mumford criterion (see [Reference MumfordMum65, Theorem 2.1]), there exists a one-parameter subgroup
$\unicode[STIX]{x1D712}={\mathcal{L}}|_{BG_{x}}$
is non-trivial. By the Hilbert–Mumford criterion (see [Reference MumfordMum65, Theorem 2.1]), there exists a one-parameter subgroup
 $\unicode[STIX]{x1D706}:\mathbb{G}_{m}\rightarrow G_{x}$
such that
$\unicode[STIX]{x1D706}:\mathbb{G}_{m}\rightarrow G_{x}$
such that
 $\lim _{t\rightarrow 0}\unicode[STIX]{x1D706}(t)\cdot w=w_{0}$
, where
$\lim _{t\rightarrow 0}\unicode[STIX]{x1D706}(t)\cdot w=w_{0}$
, where
![]() $w\in W$
and
$w\in W$
and
 $w_{0}\in W^{G_{x}}$
are points over
$w_{0}\in W^{G_{x}}$
are points over
![]() $z$
and
$z$
and
![]() $x$
, respectively. As
$x$
, respectively. As
 $w\in W_{\unicode[STIX]{x1D712}}^{+}\cap W_{\unicode[STIX]{x1D712}}^{-}$
and
$w\in W_{\unicode[STIX]{x1D712}}^{+}\cap W_{\unicode[STIX]{x1D712}}^{-}$
and
 $w_{0}\in W^{G_{x}}$
, by applying Lemma 3.2 twice with the characters
$w_{0}\in W^{G_{x}}$
, by applying Lemma 3.2 twice with the characters
![]() $\unicode[STIX]{x1D712}$
and
$\unicode[STIX]{x1D712}$
and
![]() $\unicode[STIX]{x1D712}^{-1}$
, we see that both
$\unicode[STIX]{x1D712}^{-1}$
, we see that both
 $\langle \unicode[STIX]{x1D712},\unicode[STIX]{x1D706}\rangle <0$
and
$\langle \unicode[STIX]{x1D712},\unicode[STIX]{x1D706}\rangle <0$
and
 $\langle \unicode[STIX]{x1D712},\unicode[STIX]{x1D706}\rangle >0$
, which is a contradiction.
$\langle \unicode[STIX]{x1D712},\unicode[STIX]{x1D706}\rangle >0$
, which is a contradiction.
For (ii), choose a local quotient presentation
 $f:({\mathcal{W}},w)\rightarrow ({\mathcal{X}},z)$
around
$f:({\mathcal{W}},w)\rightarrow ({\mathcal{X}},z)$
around
![]() $z$
with
$z$
with
 ${\mathcal{W}}=[W/G_{z}]$
. Let
${\mathcal{W}}=[W/G_{z}]$
. Let
 $\unicode[STIX]{x1D712}={\mathcal{L}}|_{BG_{z}}$
be the character of
$\unicode[STIX]{x1D712}={\mathcal{L}}|_{BG_{z}}$
be the character of
![]() ${\mathcal{L}}$
. Since
${\mathcal{L}}$
. Since
 $w\in W^{G_{z}}$
, the point
$w\in W^{G_{z}}$
, the point
![]() $w$
is semistable with respect to
$w$
is semistable with respect to
![]() $\unicode[STIX]{x1D712}$
if and only if
$\unicode[STIX]{x1D712}$
if and only if
![]() $\unicode[STIX]{x1D712}$
is trivial. It follows that
$\unicode[STIX]{x1D712}$
is trivial. It follows that
 $w\in {\mathcal{W}}^{+}\cap {\mathcal{W}}^{-}$
if
$w\in {\mathcal{W}}^{+}\cap {\mathcal{W}}^{-}$
if
![]() $\unicode[STIX]{x1D712}$
is trivial and
$\unicode[STIX]{x1D712}$
is trivial and
 $w\notin {\mathcal{W}}^{+}\cup {\mathcal{W}}^{-}$
otherwise.◻
$w\notin {\mathcal{W}}^{+}\cup {\mathcal{W}}^{-}$
otherwise.◻
Proof of Theorem 1.3.
We show that
![]() ${\mathcal{X}}$
has a good moduli space by verifying the hypotheses of Theorem 1.2. Let
${\mathcal{X}}$
has a good moduli space by verifying the hypotheses of Theorem 1.2. Let
![]() $x_{0}\in {\mathcal{X}}$
be a closed point. By Lemma 3.5(ii), we have either
$x_{0}\in {\mathcal{X}}$
be a closed point. By Lemma 3.5(ii), we have either
 $x_{0}\in {\mathcal{X}}^{+}\cap {\mathcal{X}}^{-}$
or
$x_{0}\in {\mathcal{X}}^{+}\cap {\mathcal{X}}^{-}$
or
 $x_{0}\in {\mathcal{Z}}^{+}\cap {\mathcal{Z}}^{-}$
. Suppose first that
$x_{0}\in {\mathcal{Z}}^{+}\cap {\mathcal{Z}}^{-}$
. Suppose first that
 $x_{0}\in {\mathcal{X}}^{+}\cap {\mathcal{X}}^{-}$
. Since
$x_{0}\in {\mathcal{X}}^{+}\cap {\mathcal{X}}^{-}$
. Since
![]() ${\mathcal{X}}^{+}$
admits a good moduli space, Proposition 2.7(iii) implies that we may choose a local quotient presentation
${\mathcal{X}}^{+}$
admits a good moduli space, Proposition 2.7(iii) implies that we may choose a local quotient presentation
 $f:{\mathcal{W}}\rightarrow {\mathcal{X}}^{+}$
around
$f:{\mathcal{W}}\rightarrow {\mathcal{X}}^{+}$
around
![]() $x_{0}$
which is strongly étale. By applying Lemma 2.8, we may shrink further to assume that
$x_{0}$
which is strongly étale. By applying Lemma 2.8, we may shrink further to assume that
 $f({\mathcal{W}})\subset {\mathcal{X}}^{+}\cap {\mathcal{X}}^{-}$
. Then Lemma 3.5(i) implies that the composition
$f({\mathcal{W}})\subset {\mathcal{X}}^{+}\cap {\mathcal{X}}^{-}$
. Then Lemma 3.5(i) implies that the composition
 $f:{\mathcal{W}}\rightarrow {\mathcal{X}}^{+}{\hookrightarrow}{\mathcal{X}}$
is also strongly étale.◻
$f:{\mathcal{W}}\rightarrow {\mathcal{X}}^{+}{\hookrightarrow}{\mathcal{X}}$
is also strongly étale.◻
On the other hand, suppose that
 $x_{0}\in {\mathcal{Z}}^{+}\cap {\mathcal{Z}}^{-}$
. Choose a local quotient presentation
$x_{0}\in {\mathcal{Z}}^{+}\cap {\mathcal{Z}}^{-}$
. Choose a local quotient presentation
 $f:({\mathcal{W}},w_{0})\rightarrow ({\mathcal{X}},x_{0})$
around
$f:({\mathcal{W}},w_{0})\rightarrow ({\mathcal{X}},x_{0})$
around
![]() $x_{0}$
inducing a Cartesian diagram
$x_{0}$
inducing a Cartesian diagram

where
 ${\mathcal{W}}^{+}={\mathcal{W}}_{{\mathcal{L}}}^{+}$
and
${\mathcal{W}}^{+}={\mathcal{W}}_{{\mathcal{L}}}^{+}$
and
 ${\mathcal{W}}^{-}={\mathcal{W}}_{{\mathcal{L}}}^{-}$
. We claim that, after shrinking suitably, we may assume that
${\mathcal{W}}^{-}={\mathcal{W}}_{{\mathcal{L}}}^{-}$
. We claim that, after shrinking suitably, we may assume that
![]() $f$
is strongly étale. In proving this claim, we make implicit repeated use of Lemma 2.8 in conjunction with Lemma 3.3 to argue that if
$f$
is strongly étale. In proving this claim, we make implicit repeated use of Lemma 2.8 in conjunction with Lemma 3.3 to argue that if
 ${\mathcal{W}}^{\prime }\subset {\mathcal{W}}$
is an open substack containing
${\mathcal{W}}^{\prime }\subset {\mathcal{W}}$
is an open substack containing
![]() $w_{0}$
, there exists an open substack
$w_{0}$
, there exists an open substack
 ${\mathcal{W}}^{\prime \prime }\subset {\mathcal{W}}^{\prime }$
containing
${\mathcal{W}}^{\prime \prime }\subset {\mathcal{W}}^{\prime }$
containing
![]() $w_{0}$
such that
$w_{0}$
such that
 ${\mathcal{W}}^{\prime \prime }\rightarrow {\mathcal{X}}$
is a local quotient presentation around
${\mathcal{W}}^{\prime \prime }\rightarrow {\mathcal{X}}$
is a local quotient presentation around
![]() $x_{0}$
inducing a Cartesian diagram as in (3.2).
$x_{0}$
inducing a Cartesian diagram as in (3.2).
Using the hypothesis that
 ${\mathcal{Z}}^{+},{\mathcal{Z}}^{-},$
and
${\mathcal{Z}}^{+},{\mathcal{Z}}^{-},$
and
![]() ${\mathcal{X}}^{+}$
admit good moduli spaces, we will first show that
${\mathcal{X}}^{+}$
admit good moduli spaces, we will first show that
![]() $f$
may be chosen to satisfy:
$f$
may be chosen to satisfy:
-
(A)
 $f|_{f^{-1}({\mathcal{Z}}^{+})}$
,
$f|_{f^{-1}({\mathcal{Z}}^{+})}$
,
 $f|_{f^{-1}({\mathcal{Z}}^{-})}$
are strongly étale; and
$f|_{f^{-1}({\mathcal{Z}}^{-})}$
are strongly étale; and -
(B)
 $f|_{{\mathcal{W}}^{+}}:{\mathcal{W}}^{+}\rightarrow {\mathcal{X}}^{+}$
is strongly étale.
$f|_{{\mathcal{W}}^{+}}:{\mathcal{W}}^{+}\rightarrow {\mathcal{X}}^{+}$
is strongly étale.
If
![]() $f$
satisfies (A) and (B), then
$f$
satisfies (A) and (B), then
![]() $f$
is also strongly étale. Indeed, if
$f$
is also strongly étale. Indeed, if
![]() $w\in {\mathcal{W}}$
is a closed point, then either
$w\in {\mathcal{W}}$
is a closed point, then either
 $w\in f^{-1}({\mathcal{Z}}^{+})\cup f^{-1}({\mathcal{Z}}^{-})$
or
$w\in f^{-1}({\mathcal{Z}}^{+})\cup f^{-1}({\mathcal{Z}}^{-})$
or
 $w\in f^{-1}({\mathcal{X}}^{+})\cap f^{-1}({\mathcal{X}}^{-})$
. In the former case, (A) immediately implies that
$w\in f^{-1}({\mathcal{X}}^{+})\cap f^{-1}({\mathcal{X}}^{-})$
. In the former case, (A) immediately implies that
![]() $f$
is stabilizer preserving at
$f$
is stabilizer preserving at
![]() $w$
and that
$w$
and that
![]() $f(w)$
is closed in
$f(w)$
is closed in
![]() ${\mathcal{X}}$
. In the latter case, (B) implies that
${\mathcal{X}}$
. In the latter case, (B) implies that
![]() $f$
is stabilizer preserving at
$f$
is stabilizer preserving at
![]() $w$
and that
$w$
and that
![]() $f(w)$
is closed in
$f(w)$
is closed in
![]() ${\mathcal{X}}^{+}$
. Since
${\mathcal{X}}^{+}$
. Since
 $f(w)\in {\mathcal{X}}^{+}\cap {\mathcal{X}}^{-}$
, Lemma 3.5(i) implies that
$f(w)\in {\mathcal{X}}^{+}\cap {\mathcal{X}}^{-}$
, Lemma 3.5(i) implies that
![]() $f(w)$
remains closed in
$f(w)$
remains closed in
![]() ${\mathcal{X}}$
.
${\mathcal{X}}$
.
It remains to show that
![]() $f$
can be chosen to satisfy (A) and (B). For (A), Proposition 2.7(iii) implies the existence of an open substack
$f$
can be chosen to satisfy (A) and (B). For (A), Proposition 2.7(iii) implies the existence of an open substack
 ${\mathcal{Q}}\subset f^{-1}({\mathcal{Z}}^{+})$
containing
${\mathcal{Q}}\subset f^{-1}({\mathcal{Z}}^{+})$
containing
![]() $w_{0}$
such that
$w_{0}$
such that
![]() $f|_{{\mathcal{Q}}}$
is strongly étale. After shrinking
$f|_{{\mathcal{Q}}}$
is strongly étale. After shrinking
![]() ${\mathcal{W}}$
suitably, we may assume that
${\mathcal{W}}$
suitably, we may assume that
 ${\mathcal{W}}\cap f^{-1}({\mathcal{Z}}^{+})\subset {\mathcal{Q}}$
. One argues similarly for
${\mathcal{W}}\cap f^{-1}({\mathcal{Z}}^{+})\subset {\mathcal{Q}}$
. One argues similarly for
 $f|_{f^{-1}({\mathcal{Z}}^{-})}$
.
$f|_{f^{-1}({\mathcal{Z}}^{-})}$
.
For (B), Proposition 2.7(iii) implies that there exists an open substack
 ${\mathcal{U}}\subset {\mathcal{W}}^{+}$
such that
${\mathcal{U}}\subset {\mathcal{W}}^{+}$
such that
 $f|_{{\mathcal{U}}}:{\mathcal{U}}\rightarrow {\mathcal{X}}^{+}$
is strongly étale and, moreover, that
$f|_{{\mathcal{U}}}:{\mathcal{U}}\rightarrow {\mathcal{X}}^{+}$
is strongly étale and, moreover, that
![]() ${\mathcal{U}}$
contains all closed points
${\mathcal{U}}$
contains all closed points
 $w\in {\mathcal{W}}^{+}$
such that
$w\in {\mathcal{W}}^{+}$
such that
 $f|_{{\mathcal{W}}^{+}}:{\mathcal{W}}^{+}\rightarrow {\mathcal{X}}^{+}$
is strongly étale at
$f|_{{\mathcal{W}}^{+}}:{\mathcal{W}}^{+}\rightarrow {\mathcal{X}}^{+}$
is strongly étale at
![]() $w$
. Let
$w$
. Let
 ${\mathcal{V}}={\mathcal{W}}^{+}\setminus {\mathcal{U}}$
and let
${\mathcal{V}}={\mathcal{W}}^{+}\setminus {\mathcal{U}}$
and let
![]() $\overline{{\mathcal{V}}}$
be the closure of
$\overline{{\mathcal{V}}}$
be the closure of
![]() ${\mathcal{V}}$
in
${\mathcal{V}}$
in
![]() ${\mathcal{W}}$
. We claim that
${\mathcal{W}}$
. We claim that
![]() $w_{0}\notin \overline{{\mathcal{V}}}$
. Once this is established, we may replace
$w_{0}\notin \overline{{\mathcal{V}}}$
. Once this is established, we may replace
![]() ${\mathcal{W}}$
by an appropriate open substack of
${\mathcal{W}}$
by an appropriate open substack of
![]() ${\mathcal{W}}\setminus \overline{{\mathcal{V}}}$
to obtain a local quotient presentation satisfying (B). Suppose, by way of contradiction, that
${\mathcal{W}}\setminus \overline{{\mathcal{V}}}$
to obtain a local quotient presentation satisfying (B). Suppose, by way of contradiction, that
![]() $w_{0}\in \overline{{\mathcal{V}}}$
. Then there exists a specialization diagram (where
$w_{0}\in \overline{{\mathcal{V}}}$
. Then there exists a specialization diagram (where
![]() $R$
is a discrete valuation ring with fraction field
$R$
is a discrete valuation ring with fraction field
![]() $K$
)
$K$
)

such that
 $h(0)=w_{0}$
. There exist good moduli spaces
$h(0)=w_{0}$
. There exist good moduli spaces
 ${\mathcal{W}}\rightarrow W$
and
${\mathcal{W}}\rightarrow W$
and
 ${\mathcal{W}}^{+}\rightarrow W^{+}$
, and the induced morphism
${\mathcal{W}}^{+}\rightarrow W^{+}$
, and the induced morphism
 $W^{+}\rightarrow W$
is proper. Since the composition
$W^{+}\rightarrow W$
is proper. Since the composition
 ${\mathcal{W}}^{+}\rightarrow W^{+}\rightarrow W$
is universally closed, there exist, after an extension of the fraction field
${\mathcal{W}}^{+}\rightarrow W^{+}\rightarrow W$
is universally closed, there exist, after an extension of the fraction field
![]() $K$
, a diagram
$K$
, a diagram

and a lift
 $\widetilde{h}:\unicode[STIX]{x1D6E5}\rightarrow {\mathcal{W}}^{+}$
that extends
$\widetilde{h}:\unicode[STIX]{x1D6E5}\rightarrow {\mathcal{W}}^{+}$
that extends
 $\unicode[STIX]{x1D6E5}^{\ast }\rightarrow {\mathcal{W}}^{+}$
with
$\unicode[STIX]{x1D6E5}^{\ast }\rightarrow {\mathcal{W}}^{+}$
with
 $\widetilde{w}=\widetilde{h}(0)\in {\mathcal{W}}^{+}$
closed. There is an isotrivial specialization
$\widetilde{w}=\widetilde{h}(0)\in {\mathcal{W}}^{+}$
closed. There is an isotrivial specialization
 $\widetilde{w}{\rightsquigarrow}w_{0}$
. It follows from Lemma 3.5(i) that
$\widetilde{w}{\rightsquigarrow}w_{0}$
. It follows from Lemma 3.5(i) that
 $\widetilde{w}\in f^{-1}({\mathcal{Z}}^{-})$
. By assumption (A),
$\widetilde{w}\in f^{-1}({\mathcal{Z}}^{-})$
. By assumption (A),
 $f|_{{\mathcal{U}}}:{\mathcal{U}}\rightarrow {\mathcal{X}}^{+}$
is strongly étale at
$f|_{{\mathcal{U}}}:{\mathcal{U}}\rightarrow {\mathcal{X}}^{+}$
is strongly étale at
![]() $\widetilde{w}$
, so that
$\widetilde{w}$
, so that
![]() $\widetilde{w}\in {\mathcal{U}}$
. On the other hand, the generic point of the specialization
$\widetilde{w}\in {\mathcal{U}}$
. On the other hand, the generic point of the specialization
 $\widetilde{h}:\unicode[STIX]{x1D6E5}\rightarrow {\mathcal{W}}^{+}$
lands in
$\widetilde{h}:\unicode[STIX]{x1D6E5}\rightarrow {\mathcal{W}}^{+}$
lands in
![]() ${\mathcal{V}}$
, so that
${\mathcal{V}}$
, so that
![]() $\widetilde{w}\in {\mathcal{V}}$
, which is a contradiction. Thus,
$\widetilde{w}\in {\mathcal{V}}$
, which is a contradiction. Thus,
![]() $w_{0}\notin \overline{{\mathcal{V}}}$
, as desired.
$w_{0}\notin \overline{{\mathcal{V}}}$
, as desired.
We have now shown that
![]() ${\mathcal{X}}$
satisfies condition (1) in Theorem 1.2, and it remains to verify condition (2). Let
${\mathcal{X}}$
satisfies condition (1) in Theorem 1.2, and it remains to verify condition (2). Let
 $x\in {\mathcal{X}}(k)$
. If
$x\in {\mathcal{X}}(k)$
. If
![]() $x\in {\mathcal{Z}}^{+}$
(respectively,
$x\in {\mathcal{Z}}^{+}$
(respectively,
![]() $x\in {\mathcal{Z}}^{-}$
), then
$x\in {\mathcal{Z}}^{-}$
), then
 $\overline{\{x\}}\subset {\mathcal{Z}}^{+}$
(respectively,
$\overline{\{x\}}\subset {\mathcal{Z}}^{+}$
(respectively,
 $\overline{\{x\}}\subset {\mathcal{Z}}^{-}$
). Therefore, since
$\overline{\{x\}}\subset {\mathcal{Z}}^{-}$
). Therefore, since
![]() ${\mathcal{Z}}^{+}$
(respectively,
${\mathcal{Z}}^{+}$
(respectively,
![]() ${\mathcal{Z}}^{-}$
) admits a good moduli space, so does
${\mathcal{Z}}^{-}$
) admits a good moduli space, so does
![]() $\overline{\{x\}}$
. On the other hand, if
$\overline{\{x\}}$
. On the other hand, if
 $x\in {\mathcal{X}}^{+}\cap {\mathcal{X}}^{-}$
, then Lemma 3.5(i) implies that the closure of
$x\in {\mathcal{X}}^{+}\cap {\mathcal{X}}^{-}$
, then Lemma 3.5(i) implies that the closure of
![]() $x$
in
$x$
in
![]() ${\mathcal{X}}$
is contained in
${\mathcal{X}}$
is contained in
![]() ${\mathcal{X}}^{+}$
. Since
${\mathcal{X}}^{+}$
. Since
![]() ${\mathcal{X}}^{+}$
admits a good moduli space, so does
${\mathcal{X}}^{+}$
admits a good moduli space, so does
![]() $\overline{\{x\}}$
. Now Theorem 1.2 implies that
$\overline{\{x\}}$
. Now Theorem 1.2 implies that
![]() ${\mathcal{X}}$
admits a good moduli space
${\mathcal{X}}$
admits a good moduli space
 $\unicode[STIX]{x1D719}:{\mathcal{X}}\rightarrow X$
.
$\unicode[STIX]{x1D719}:{\mathcal{X}}\rightarrow X$
.
Next, we will apply Proposition 3.1 to show that
![]() ${\mathcal{X}}^{-}$
admits a good moduli space. Let
${\mathcal{X}}^{-}$
admits a good moduli space. Let
![]() $x\in {\mathcal{X}}^{-}$
be a closed point and
$x\in {\mathcal{X}}^{-}$
be a closed point and
![]() $x{\rightsquigarrow}x_{0}$
be the isotrivial specialization to the unique closed point
$x{\rightsquigarrow}x_{0}$
be the isotrivial specialization to the unique closed point
![]() $x_{0}\in {\mathcal{X}}$
in its closure. By Proposition 2.7, there exists a strongly étale local quotient presentation
$x_{0}\in {\mathcal{X}}$
in its closure. By Proposition 2.7, there exists a strongly étale local quotient presentation
 $f:{\mathcal{W}}\rightarrow {\mathcal{X}}$
around
$f:{\mathcal{W}}\rightarrow {\mathcal{X}}$
around
![]() $x_{0}$
inducing a Cartesian diagram as in (1.2). By Lemma 2.9, the base change
$x_{0}$
inducing a Cartesian diagram as in (1.2). By Lemma 2.9, the base change
 $f^{-}:{\mathcal{W}}^{-}\rightarrow {\mathcal{X}}^{-}$
is strongly étale. As
$f^{-}:{\mathcal{W}}^{-}\rightarrow {\mathcal{X}}^{-}$
is strongly étale. As
![]() ${\mathcal{W}}^{-}$
admits a good moduli space, we may shrink
${\mathcal{W}}^{-}$
admits a good moduli space, we may shrink
![]() ${\mathcal{W}}^{-}$
further so that
${\mathcal{W}}^{-}$
further so that
 $f^{-}:{\mathcal{W}}^{-}\rightarrow {\mathcal{X}}^{-}$
is a strongly étale neighborhood of
$f^{-}:{\mathcal{W}}^{-}\rightarrow {\mathcal{X}}^{-}$
is a strongly étale neighborhood of
![]() $x$
.
$x$
.
It remains to check that if
 $x\in {\mathcal{X}}^{-}(k)$
is any point, then its closure
$x\in {\mathcal{X}}^{-}(k)$
is any point, then its closure
![]() $\overline{\{x\}}$
in
$\overline{\{x\}}$
in
![]() ${\mathcal{X}}^{-}$
admits a good moduli space. Let
${\mathcal{X}}^{-}$
admits a good moduli space. Let
![]() $x{\rightsquigarrow}x_{0}$
be the isotrivial specialization to the unique closed point
$x{\rightsquigarrow}x_{0}$
be the isotrivial specialization to the unique closed point
![]() $x_{0}\in {\mathcal{X}}$
in the closure of
$x_{0}\in {\mathcal{X}}$
in the closure of
![]() $x$
. We claim in fact that
$x$
. We claim in fact that
 $\unicode[STIX]{x1D719}^{-1}(\unicode[STIX]{x1D719}(x_{0}))\cap {\mathcal{X}}^{-}$
admits a good moduli space, which in turn clearly implies that
$\unicode[STIX]{x1D719}^{-1}(\unicode[STIX]{x1D719}(x_{0}))\cap {\mathcal{X}}^{-}$
admits a good moduli space, which in turn clearly implies that
 $\overline{\{x\}}\subset {\mathcal{X}}^{-}$
does as well. We can choose a local quotient presentation
$\overline{\{x\}}\subset {\mathcal{X}}^{-}$
does as well. We can choose a local quotient presentation
 $f:({\mathcal{W}},w_{0})\rightarrow ({\mathcal{X}},x_{0})$
around
$f:({\mathcal{W}},w_{0})\rightarrow ({\mathcal{X}},x_{0})$
around
![]() $x_{0}$
inducing a Cartesian diagram as in (1.2). After shrinking, we may assume by Proposition 2.7(iii) that
$x_{0}$
inducing a Cartesian diagram as in (1.2). After shrinking, we may assume by Proposition 2.7(iii) that
![]() $f$
is strongly étale and we may also assume that
$f$
is strongly étale and we may also assume that
![]() $w_{0}$
is the unique preimage of
$w_{0}$
is the unique preimage of
![]() $x_{0}$
. If we set
$x_{0}$
. If we set
 ${\mathcal{Z}}=\unicode[STIX]{x1D719}^{-1}(\unicode[STIX]{x1D719}(x_{0}))$
, then
${\mathcal{Z}}=\unicode[STIX]{x1D719}^{-1}(\unicode[STIX]{x1D719}(x_{0}))$
, then
 $f|_{f^{-1}({\mathcal{Z}})}:f^{-1}({\mathcal{Z}})\rightarrow {\mathcal{Z}}$
is in fact an isomorphism as both
$f|_{f^{-1}({\mathcal{Z}})}:f^{-1}({\mathcal{Z}})\rightarrow {\mathcal{Z}}$
is in fact an isomorphism as both
![]() $f^{-1}({\mathcal{Z}})$
and
$f^{-1}({\mathcal{Z}})$
and
![]() ${\mathcal{Z}}$
have
${\mathcal{Z}}$
have
![]() $\operatorname{Spec}k$
as a good moduli space. As
$\operatorname{Spec}k$
as a good moduli space. As
![]() ${\mathcal{W}}^{-}$
admits a good moduli space, so does
${\mathcal{W}}^{-}$
admits a good moduli space, so does
 ${\mathcal{W}}^{-}\cap f^{-1}({\mathcal{Z}})={\mathcal{X}}^{-}\cap {\mathcal{Z}}$
. This establishes that
${\mathcal{W}}^{-}\cap f^{-1}({\mathcal{Z}})={\mathcal{X}}^{-}\cap {\mathcal{Z}}$
. This establishes that
![]() ${\mathcal{X}}^{-}$
admits a good moduli space.
${\mathcal{X}}^{-}$
admits a good moduli space.
Finally, we argue that
 $X^{+}\rightarrow X$
and
$X^{+}\rightarrow X$
and
 $X^{-}\rightarrow X$
are proper and surjective. By taking a disjoint union of local quotient presentations and applying Proposition 2.7(iii), there exists an affine, strongly étale, and surjective morphism
$X^{-}\rightarrow X$
are proper and surjective. By taking a disjoint union of local quotient presentations and applying Proposition 2.7(iii), there exists an affine, strongly étale, and surjective morphism
 $f:{\mathcal{W}}\rightarrow {\mathcal{X}}$
from an algebraic stack admitting a good moduli space
$f:{\mathcal{W}}\rightarrow {\mathcal{X}}$
from an algebraic stack admitting a good moduli space
 ${\mathcal{W}}\rightarrow W$
such that
${\mathcal{W}}\rightarrow W$
such that
 ${\mathcal{W}}={\mathcal{X}}\times _{X}W$
. Moreover, if we set
${\mathcal{W}}={\mathcal{X}}\times _{X}W$
. Moreover, if we set
 ${\mathcal{W}}^{+}:=f^{-1}({\mathcal{X}}^{+})$
and
${\mathcal{W}}^{+}:=f^{-1}({\mathcal{X}}^{+})$
and
 ${\mathcal{W}}^{-}:=f^{-1}({\mathcal{X}}^{-})$
, then
${\mathcal{W}}^{-}:=f^{-1}({\mathcal{X}}^{-})$
, then
![]() ${\mathcal{W}}^{+}$
and
${\mathcal{W}}^{+}$
and
![]() ${\mathcal{W}}^{-}$
admit good moduli spaces
${\mathcal{W}}^{-}$
admit good moduli spaces
![]() $W^{+}$
and
$W^{+}$
and
![]() $W^{-}$
such that
$W^{-}$
such that
 $W^{-}\rightarrow W$
and
$W^{-}\rightarrow W$
and
 $W^{+}\rightarrow W$
are proper and surjective. This gives commutative cubes
$W^{+}\rightarrow W$
are proper and surjective. This gives commutative cubes

As
 $f|_{{\mathcal{W}}^{+}}:{\mathcal{W}}^{+}\rightarrow {\mathcal{X}}^{+}$
and
$f|_{{\mathcal{W}}^{+}}:{\mathcal{W}}^{+}\rightarrow {\mathcal{X}}^{+}$
and
 $f|_{{\mathcal{W}}^{-}}:{\mathcal{W}}^{-}\rightarrow {\mathcal{X}}^{-}$
are strongly étale (Lemma 2.9), the left- and right-hand faces are Cartesian squares. Since the top faces are also Cartesian, we have
$f|_{{\mathcal{W}}^{-}}:{\mathcal{W}}^{-}\rightarrow {\mathcal{X}}^{-}$
are strongly étale (Lemma 2.9), the left- and right-hand faces are Cartesian squares. Since the top faces are also Cartesian, we have
 ${\mathcal{W}}^{+}\simeq {\mathcal{X}}^{+}\times _{X}W$
and
${\mathcal{W}}^{+}\simeq {\mathcal{X}}^{+}\times _{X}W$
and
 ${\mathcal{W}}^{-}\simeq {\mathcal{X}}^{-}\times _{X}W$
. In particular,
${\mathcal{W}}^{-}\simeq {\mathcal{X}}^{-}\times _{X}W$
. In particular,
 ${\mathcal{W}}^{+}\rightarrow X^{+}\times _{X}W$
and
${\mathcal{W}}^{+}\rightarrow X^{+}\times _{X}W$
and
 ${\mathcal{W}}^{-}\rightarrow X^{-}\times _{X}W$
are good moduli spaces. By uniqueness of good moduli spaces, we have
${\mathcal{W}}^{-}\rightarrow X^{-}\times _{X}W$
are good moduli spaces. By uniqueness of good moduli spaces, we have
 $X^{+}\times _{X}W\simeq W^{+}$
and
$X^{+}\times _{X}W\simeq W^{+}$
and
 $X^{-}\times _{X}W\simeq W^{-}$
. Since
$X^{-}\times _{X}W\simeq W^{-}$
. Since
 $W^{+}\rightarrow W$
and
$W^{+}\rightarrow W$
and
 $W^{-}\rightarrow W$
are proper and surjective,
$W^{-}\rightarrow W$
are proper and surjective,
 $X^{+}\rightarrow X$
and
$X^{+}\rightarrow X$
and
 $X^{-}\rightarrow X$
are proper and surjective by étale descent.
$X^{-}\rightarrow X$
are proper and surjective by étale descent.
3.3 Existence via finite covers
In proving Proposition 1.4, we will appeal to the following lemma.
Lemma 3.6. Consider a commutative diagram

of algebraic stacks of finite type over an algebraically closed field
![]() $k$
of characteristic
$k$
of characteristic
![]() $0$
, where
$0$
, where
![]() $X$
is an algebraic space. Suppose that:
$X$
is an algebraic space. Suppose that:
-
(i) the morphism
 ${\mathcal{X}}\rightarrow {\mathcal{Y}}$
is finite and surjective;
${\mathcal{X}}\rightarrow {\mathcal{Y}}$
is finite and surjective; -
(ii) the morphism
 ${\mathcal{X}}\rightarrow X$
is cohomologically affine; and
${\mathcal{X}}\rightarrow X$
is cohomologically affine; and -
(iii) the algebraic stack
 ${\mathcal{Y}}$
is a global quotient stack.
${\mathcal{Y}}$
is a global quotient stack.
Then
![]() ${\mathcal{Y}}\rightarrow X$
is cohomologically affine.
${\mathcal{Y}}\rightarrow X$
is cohomologically affine.
Proof. We may write
 ${\mathcal{Y}}=[V/\text{GL}_{n}]$
, where
${\mathcal{Y}}=[V/\text{GL}_{n}]$
, where
![]() $V$
is an algebraic space with an action of
$V$
is an algebraic space with an action of
![]() $\operatorname{GL}_{n}$
. Since
$\operatorname{GL}_{n}$
. Since
![]() ${\mathcal{X}}\rightarrow {\mathcal{Y}}$
is affine,
${\mathcal{X}}\rightarrow {\mathcal{Y}}$
is affine,
![]() ${\mathcal{X}}$
is the quotient stack
${\mathcal{X}}$
is the quotient stack
 ${\mathcal{X}}=[U/\text{GL}_{n}]$
, where
${\mathcal{X}}=[U/\text{GL}_{n}]$
, where
 $U={\mathcal{X}}\times _{{\mathcal{Y}}}V$
. Since
$U={\mathcal{X}}\times _{{\mathcal{Y}}}V$
. Since
![]() $U\rightarrow {\mathcal{X}}$
is affine and
$U\rightarrow {\mathcal{X}}$
is affine and
 ${\mathcal{X}}\rightarrow X$
is cohomologically affine, the morphism
${\mathcal{X}}\rightarrow X$
is cohomologically affine, the morphism
![]() $U\rightarrow X$
is affine by Serre’s criterion. The morphism
$U\rightarrow X$
is affine by Serre’s criterion. The morphism
![]() $U\rightarrow V$
is finite and surjective and therefore, by Chevalley’s theorem, we can conclude that
$U\rightarrow V$
is finite and surjective and therefore, by Chevalley’s theorem, we can conclude that
 $V\rightarrow X$
is affine. Therefore,
$V\rightarrow X$
is affine. Therefore,
 ${\mathcal{Y}}\rightarrow X$
is cohomologically affine.◻
${\mathcal{Y}}\rightarrow X$
is cohomologically affine.◻
Proof of Proposition 1.4.
Let
![]() ${\mathcal{Z}}$
be the scheme-theoretic image of
${\mathcal{Z}}$
be the scheme-theoretic image of
 ${\mathcal{X}}\rightarrow X\times {\mathcal{Y}}$
. Since
${\mathcal{X}}\rightarrow X\times {\mathcal{Y}}$
. Since
![]() ${\mathcal{X}}\rightarrow {\mathcal{Y}}$
is finite and
${\mathcal{X}}\rightarrow {\mathcal{Y}}$
is finite and
![]() $X$
is separated,
$X$
is separated,
 ${\mathcal{X}}\rightarrow {\mathcal{Z}}$
is finite. Since
${\mathcal{X}}\rightarrow {\mathcal{Z}}$
is finite. Since
![]() ${\mathcal{Z}}$
is a global quotient stack (as
${\mathcal{Z}}$
is a global quotient stack (as
![]() ${\mathcal{Y}}$
is), we may apply Lemma 3.6 to conclude that the projection
${\mathcal{Y}}$
is), we may apply Lemma 3.6 to conclude that the projection
 ${\mathcal{Z}}\rightarrow X$
is cohomologically affine, which implies that
${\mathcal{Z}}\rightarrow X$
is cohomologically affine, which implies that
![]() ${\mathcal{Z}}$
admits a separated good moduli space. The composition
${\mathcal{Z}}$
admits a separated good moduli space. The composition
 ${\mathcal{Z}}{\hookrightarrow}X\times {\mathcal{Y}}\rightarrow {\mathcal{Y}}$
is finite, surjective, and stabilizer preserving at closed points. Therefore, by replacing
${\mathcal{Z}}{\hookrightarrow}X\times {\mathcal{Y}}\rightarrow {\mathcal{Y}}$
is finite, surjective, and stabilizer preserving at closed points. Therefore, by replacing
![]() ${\mathcal{X}}$
with
${\mathcal{X}}$
with
![]() ${\mathcal{Z}}$
, to prove the proposition, we may assume that
${\mathcal{Z}}$
, to prove the proposition, we may assume that
 $f:{\mathcal{X}}\rightarrow {\mathcal{Y}}$
is stabilizer preserving at closed points.◻
$f:{\mathcal{X}}\rightarrow {\mathcal{Y}}$
is stabilizer preserving at closed points.◻
We will now show that the hypotheses of Theorem 1.2 are satisfied. Let
![]() $y_{0}\in {\mathcal{Y}}$
be a closed point and
$y_{0}\in {\mathcal{Y}}$
be a closed point and
 $g:({\mathcal{Y}}^{\prime },y_{0}^{\prime })\rightarrow ({\mathcal{Y}},y_{0})$
be a local quotient presentation around
$g:({\mathcal{Y}}^{\prime },y_{0}^{\prime })\rightarrow ({\mathcal{Y}},y_{0})$
be a local quotient presentation around
![]() $y_{0}$
. Consider the Cartesian diagram
$y_{0}$
. Consider the Cartesian diagram

We first note that
![]() $g^{\prime }$
is strongly étale at each point
$g^{\prime }$
is strongly étale at each point
 $x^{\prime }\in {f^{\prime }}^{-1}(y_{0}^{\prime })$
. Indeed,
$x^{\prime }\in {f^{\prime }}^{-1}(y_{0}^{\prime })$
. Indeed,
![]() $g^{\prime }$
is stabilizer preserving at
$g^{\prime }$
is stabilizer preserving at
![]() $x^{\prime }$
as
$x^{\prime }$
as
![]() $g$
is stabilizer preserving at
$g$
is stabilizer preserving at
![]() $y_{0}^{\prime }$
, and
$y_{0}^{\prime }$
, and
 $g^{\prime }(x^{\prime })\in {\mathcal{X}}$
is closed as
$g^{\prime }(x^{\prime })\in {\mathcal{X}}$
is closed as
 $f(g^{\prime }(x^{\prime }))\in {\mathcal{Y}}$
is closed. By Proposition 2.7, there exists an open substack
$f(g^{\prime }(x^{\prime }))\in {\mathcal{Y}}$
is closed. By Proposition 2.7, there exists an open substack
 ${\mathcal{U}}^{\prime }\subset {\mathcal{X}}^{\prime }$
containing the fiber over
${\mathcal{U}}^{\prime }\subset {\mathcal{X}}^{\prime }$
containing the fiber over
![]() $y_{0}^{\prime }$
such that
$y_{0}^{\prime }$
such that
![]() $g^{\prime }|_{{\mathcal{U}}^{\prime }}$
is strongly étale. Therefore,
$g^{\prime }|_{{\mathcal{U}}^{\prime }}$
is strongly étale. Therefore,
 $y_{0}^{\prime }\notin {\mathcal{Z}}=f^{\prime }({\mathcal{X}}^{\prime }\setminus {\mathcal{U}}^{\prime })$
and
$y_{0}^{\prime }\notin {\mathcal{Z}}=f^{\prime }({\mathcal{X}}^{\prime }\setminus {\mathcal{U}}^{\prime })$
and
![]() $g|_{{\mathcal{Y}}^{\prime }\setminus {\mathcal{Z}}}$
is strongly étale. By shrinking further using Lemma 2.8, we obtain a local quotient presentation
$g|_{{\mathcal{Y}}^{\prime }\setminus {\mathcal{Z}}}$
is strongly étale. By shrinking further using Lemma 2.8, we obtain a local quotient presentation
 $g:{\mathcal{Y}}^{\prime }\rightarrow {\mathcal{Y}}$
around
$g:{\mathcal{Y}}^{\prime }\rightarrow {\mathcal{Y}}$
around
![]() $y_{0}$
which is strongly étale.
$y_{0}$
which is strongly étale.
Finally, let
 $y\in {\mathcal{Y}}(k)$
and
$y\in {\mathcal{Y}}(k)$
and
 $x\in {\mathcal{X}}(k)$
be any preimage. Set
$x\in {\mathcal{X}}(k)$
be any preimage. Set
 ${\mathcal{X}}_{0}=\overline{\{x\}}\subset {\mathcal{X}}$
and
${\mathcal{X}}_{0}=\overline{\{x\}}\subset {\mathcal{X}}$
and
 ${\mathcal{Y}}_{0}=\overline{\{y\}}\subset {\mathcal{Y}}$
. As
${\mathcal{Y}}_{0}=\overline{\{y\}}\subset {\mathcal{Y}}$
. As
 ${\mathcal{X}}_{0}\rightarrow {\mathcal{Y}}_{0}$
is finite and surjective,
${\mathcal{X}}_{0}\rightarrow {\mathcal{Y}}_{0}$
is finite and surjective,
 ${\mathcal{X}}_{0}\rightarrow \operatorname{Spec}k$
is a good moduli space, and
${\mathcal{X}}_{0}\rightarrow \operatorname{Spec}k$
is a good moduli space, and
![]() ${\mathcal{Y}}_{0}$
is a global quotient stack, we may conclude using Lemma 3.6 that
${\mathcal{Y}}_{0}$
is a global quotient stack, we may conclude using Lemma 3.6 that
![]() ${\mathcal{Y}}_{0}$
admits a good moduli space. Therefore, we may apply Theorem 1.2 to establish the proposition.
${\mathcal{Y}}_{0}$
admits a good moduli space. Therefore, we may apply Theorem 1.2 to establish the proposition.
Remark.
The hypothesis that
![]() $X$
is separated in Proposition 1.4 is necessary. For example, let
$X$
is separated in Proposition 1.4 is necessary. For example, let
![]() $X$
be the affine line with
$X$
be the affine line with
![]() $0$
doubled and let
$0$
doubled and let
![]() $\mathbb{Z}_{2}$
act on
$\mathbb{Z}_{2}$
act on
![]() $X$
by swapping the points at
$X$
by swapping the points at
![]() $0$
and fixing all other points. Then
$0$
and fixing all other points. Then
 $X\rightarrow [X/\mathbb{Z}_{2}]$
satisfies the hypotheses but
$X\rightarrow [X/\mathbb{Z}_{2}]$
satisfies the hypotheses but
![]() $[X/\mathbb{Z}_{2}]$
does not admit a good moduli space.
$[X/\mathbb{Z}_{2}]$
does not admit a good moduli space.
4 Application to
 $\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC})$
$\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC})$
In this section, we apply Theorem 1.3 to prove that the algebraic stacks
 $\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC})$
admit good moduli spaces (Theorem 1.1). We already know that the inclusions
$\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC})$
admit good moduli spaces (Theorem 1.1). We already know that the inclusions
 $$\begin{eqnarray}\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D716}){\hookrightarrow}\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}){\hookleftarrow}\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D716})\end{eqnarray}$$
$$\begin{eqnarray}\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D716}){\hookrightarrow}\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}){\hookleftarrow}\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D716})\end{eqnarray}$$
arise from local VGIT with respect to
![]() $\unicode[STIX]{x1D6FF}-\unicode[STIX]{x1D713}$
[Reference Alper, Fedorchuk, Smyth and van der WyckAFSvdW17, Theorem 3.17]. Thus, it only remains to show that for each critical value
$\unicode[STIX]{x1D6FF}-\unicode[STIX]{x1D713}$
[Reference Alper, Fedorchuk, Smyth and van der WyckAFSvdW17, Theorem 3.17]. Thus, it only remains to show that for each critical value
 $\unicode[STIX]{x1D6FC}_{c}\in \{9/11,7/10,2/3\}$
, the closed substacks
$\unicode[STIX]{x1D6FC}_{c}\in \{9/11,7/10,2/3\}$
, the closed substacks
 $$\begin{eqnarray}\displaystyle \overline{{\mathcal{S}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c}) & := & \displaystyle \overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})\setminus \overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c}+\unicode[STIX]{x1D716}),\nonumber\\ \displaystyle \overline{{\mathcal{H}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c}) & := & \displaystyle \overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})\setminus \overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c}-\unicode[STIX]{x1D716})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \overline{{\mathcal{S}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c}) & := & \displaystyle \overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})\setminus \overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c}+\unicode[STIX]{x1D716}),\nonumber\\ \displaystyle \overline{{\mathcal{H}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c}) & := & \displaystyle \overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})\setminus \overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c}-\unicode[STIX]{x1D716})\nonumber\end{eqnarray}$$
admit good moduli spaces. We will prove this statement by induction on
![]() $g$
. As with the boundary strata of
$g$
. As with the boundary strata of
![]() $\overline{{\mathcal{M}}}_{g,n}$
,
$\overline{{\mathcal{M}}}_{g,n}$
,
 $\overline{{\mathcal{H}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
can be described (up to a finite cover) as a product of moduli spaces of
$\overline{{\mathcal{H}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
can be described (up to a finite cover) as a product of moduli spaces of
![]() $\unicode[STIX]{x1D6FC}_{c}$
-stable curves of lower genus. Likewise,
$\unicode[STIX]{x1D6FC}_{c}$
-stable curves of lower genus. Likewise,
 $\overline{{\mathcal{S}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
can be described (up to a finite cover) as stacky projective bundles over moduli spaces of
$\overline{{\mathcal{S}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
can be described (up to a finite cover) as stacky projective bundles over moduli spaces of
![]() $\unicode[STIX]{x1D6FC}_{c}$
-stable curves of lower genus. We use induction to deduce that these products and projective bundles admit good moduli spaces, and then apply Proposition 1.4 to conclude that
$\unicode[STIX]{x1D6FC}_{c}$
-stable curves of lower genus. We use induction to deduce that these products and projective bundles admit good moduli spaces, and then apply Proposition 1.4 to conclude that
 $\overline{{\mathcal{S}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
and
$\overline{{\mathcal{S}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
and
 $\overline{{\mathcal{H}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
admit good moduli spaces.
$\overline{{\mathcal{H}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
admit good moduli spaces.
4.1 Properties of
 $\unicode[STIX]{x1D6FC}$
-stability
$\unicode[STIX]{x1D6FC}$
-stability
We will make repeated use of the following elementary properties of
![]() $\unicode[STIX]{x1D6FC}$
-stability.
$\unicode[STIX]{x1D6FC}$
-stability.
Lemma 4.1 [Reference Alper, Fedorchuk, Smyth and van der WyckAFSvdW17, Lemma 2.17].
(i) If
 $(\widetilde{C}_{1},\{p_{i}\}_{i=1}^{n},q_{1})$
and
$(\widetilde{C}_{1},\{p_{i}\}_{i=1}^{n},q_{1})$
and
 $(\widetilde{C}_{2},\{p_{i}\}_{i=1}^{n},q_{2})$
are
$(\widetilde{C}_{2},\{p_{i}\}_{i=1}^{n},q_{2})$
are
![]() $\unicode[STIX]{x1D6FC}$
-stable curves, then
$\unicode[STIX]{x1D6FC}$
-stable curves, then
 $$\begin{eqnarray}(\widetilde{C}_{1},\{p_{i}\}_{i=1}^{n},q_{1})\cup (\widetilde{C}_{2},\{p_{i}\}_{i=1}^{n},q_{2})/(q_{1}\sim q_{2})\end{eqnarray}$$
$$\begin{eqnarray}(\widetilde{C}_{1},\{p_{i}\}_{i=1}^{n},q_{1})\cup (\widetilde{C}_{2},\{p_{i}\}_{i=1}^{n},q_{2})/(q_{1}\sim q_{2})\end{eqnarray}$$
is
![]() $\unicode[STIX]{x1D6FC}$
-stable.
$\unicode[STIX]{x1D6FC}$
-stable.
(ii) If
 $(\widetilde{C},\{p_{i}\}_{i=1}^{n},q_{1},q_{2})$
is an
$(\widetilde{C},\{p_{i}\}_{i=1}^{n},q_{1},q_{2})$
is an
![]() $\unicode[STIX]{x1D6FC}$
-stable curve, then
$\unicode[STIX]{x1D6FC}$
-stable curve, then
 $$\begin{eqnarray}(\widetilde{C},\{p_{i}\}_{i=1}^{n},q_{1},q_{2})/(q_{1}\sim q_{2})\end{eqnarray}$$
$$\begin{eqnarray}(\widetilde{C},\{p_{i}\}_{i=1}^{n},q_{1},q_{2})/(q_{1}\sim q_{2})\end{eqnarray}$$
is
![]() $\unicode[STIX]{x1D6FC}$
-stable provided one of the following conditions hold:
$\unicode[STIX]{x1D6FC}$
-stable provided one of the following conditions hold:
-
–
 $q_{1}$
and
$q_{1}$
and
 $q_{2}$
lie on disjoint irreducible components of
$q_{2}$
lie on disjoint irreducible components of
 $\widetilde{C}$
;
$\widetilde{C}$
; -
–
 $q_{1}$
and
$q_{1}$
and
 $q_{2}$
lie on distinct irreducible components of
$q_{2}$
lie on distinct irreducible components of
 $\widetilde{C}$
, and at least one of these components is not a smooth rational curve.
$\widetilde{C}$
, and at least one of these components is not a smooth rational curve.
Lemma 4.2 [Reference Alper, Fedorchuk, Smyth and van der WyckAFSvdW17, Lemma 2.19].
Let
 $(C,\{p_{i}\}_{i=1}^{n})$
be an
$(C,\{p_{i}\}_{i=1}^{n})$
be an
![]() $n$
-pointed curve with
$n$
-pointed curve with
 $\unicode[STIX]{x1D714}_{C}(\sum _{i}p_{i})$
ample, and suppose that
$\unicode[STIX]{x1D714}_{C}(\sum _{i}p_{i})$
ample, and suppose that
![]() $q\in C$
is an
$q\in C$
is an
![]() $\unicode[STIX]{x1D6FC}_{c}$
-critical singularity. Then the stable pointed normalization of
$\unicode[STIX]{x1D6FC}_{c}$
-critical singularity. Then the stable pointed normalization of
 $(C,\{p_{i}\}_{i=1}^{n})$
at
$(C,\{p_{i}\}_{i=1}^{n})$
at
![]() $q\in C$
is
$q\in C$
is
![]() $\unicode[STIX]{x1D6FC}_{c}$
-stable if and only if
$\unicode[STIX]{x1D6FC}_{c}$
-stable if and only if
 $(C,\{p_{i}\}_{i=1}^{n})$
is
$(C,\{p_{i}\}_{i=1}^{n})$
is
![]() $\unicode[STIX]{x1D6FC}_{c}$
-stable.
$\unicode[STIX]{x1D6FC}_{c}$
-stable.
4.2 Existence for
 $\overline{{\mathcal{S}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
$\overline{{\mathcal{S}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
In this section, we use induction on
![]() $g$
to prove that
$g$
to prove that
 $\overline{{\mathcal{S}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
admits a good moduli space. The base case is handled by the following lemma.
$\overline{{\mathcal{S}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
admits a good moduli space. The base case is handled by the following lemma.
Lemma 4.3. We have
 $$\begin{eqnarray}\displaystyle \overline{{\mathcal{S}}}_{1,1}(9/11) & \simeq & \displaystyle B\mathbb{G}_{m},\nonumber\\ \displaystyle \overline{{\mathcal{S}}}_{1,2}(7/10) & \simeq & \displaystyle B\mathbb{G}_{m},\quad \text{and}\nonumber\\ \displaystyle \overline{{\mathcal{S}}}_{2,1}(2/3) & \simeq & \displaystyle [\mathbb{A}^{1}/\mathbb{G}_{m}],\quad \text{where }\mathbb{G}_{m}\text{ acts with weight }1.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \overline{{\mathcal{S}}}_{1,1}(9/11) & \simeq & \displaystyle B\mathbb{G}_{m},\nonumber\\ \displaystyle \overline{{\mathcal{S}}}_{1,2}(7/10) & \simeq & \displaystyle B\mathbb{G}_{m},\quad \text{and}\nonumber\\ \displaystyle \overline{{\mathcal{S}}}_{2,1}(2/3) & \simeq & \displaystyle [\mathbb{A}^{1}/\mathbb{G}_{m}],\quad \text{where }\mathbb{G}_{m}\text{ acts with weight }1.\nonumber\end{eqnarray}$$
In particular, the algebraic stacks
 $\overline{{\mathcal{S}}}_{1,1}(9/11)$
,
$\overline{{\mathcal{S}}}_{1,1}(9/11)$
,
 $\overline{{\mathcal{S}}}_{1,2}(7/10)$
, and
$\overline{{\mathcal{S}}}_{1,2}(7/10)$
, and
 $\overline{{\mathcal{S}}}_{2,1}(2/3)$
admit good moduli spaces.
$\overline{{\mathcal{S}}}_{2,1}(2/3)$
admit good moduli spaces.
Proof. The algebraic stacks
 $\overline{{\mathcal{S}}}_{1,1}(9/11)$
and
$\overline{{\mathcal{S}}}_{1,1}(9/11)$
and
 $\overline{{\mathcal{S}}}_{1,2}(7/10)$
each contain a unique
$\overline{{\mathcal{S}}}_{1,2}(7/10)$
each contain a unique
![]() $\mathbb{C}$
-point, namely the
$\mathbb{C}$
-point, namely the
![]() $9/11$
-atom and the
$9/11$
-atom and the
![]() $7/10$
-atom, and each of these curves has a
$7/10$
-atom, and each of these curves has a
![]() $\mathbb{G}_{m}$
-automorphism group. The stack
$\mathbb{G}_{m}$
-automorphism group. The stack
 $\overline{{\mathcal{S}}}_{2,1}(2/3)$
contains two isomorphism classes of curves, namely the
$\overline{{\mathcal{S}}}_{2,1}(2/3)$
contains two isomorphism classes of curves, namely the
![]() $2/3$
-atom, and the rational ramphoid cuspidal curve with non-trivial crimping. We construct this stack explicitly as follows: start with the constant family
$2/3$
-atom, and the rational ramphoid cuspidal curve with non-trivial crimping. We construct this stack explicitly as follows: start with the constant family
 $(\mathbb{P}^{1}\times \mathbb{A}^{1},\infty \times \mathbb{A}^{1})$
, let
$(\mathbb{P}^{1}\times \mathbb{A}^{1},\infty \times \mathbb{A}^{1})$
, let
![]() $c$
be a coordinate on
$c$
be a coordinate on
![]() $\mathbb{A}^{1}$
, and
$\mathbb{A}^{1}$
, and
![]() $t$
a coordinate on
$t$
a coordinate on
![]() $\mathbb{P}^{1}-\infty$
. Now let
$\mathbb{P}^{1}-\infty$
. Now let
 $\mathbb{P}^{1}\times \mathbb{A}^{1}\rightarrow {\mathcal{C}}$
be the map defined by the inclusion of algebras
$\mathbb{P}^{1}\times \mathbb{A}^{1}\rightarrow {\mathcal{C}}$
be the map defined by the inclusion of algebras
 $\mathbb{C}[t^{2}+ct^{3},t^{5}]\subset \mathbb{C}[c,t]$
on the complement of the infinity section, and defined as an isomorphism on the complement of the zero section. Then
$\mathbb{C}[t^{2}+ct^{3},t^{5}]\subset \mathbb{C}[c,t]$
on the complement of the infinity section, and defined as an isomorphism on the complement of the zero section. Then
 $({\mathcal{C}}\rightarrow \mathbb{A}^{1},\infty \times \mathbb{A}^{1})$
is a family of rational ramphoid cuspidal curves whose fiber over
$({\mathcal{C}}\rightarrow \mathbb{A}^{1},\infty \times \mathbb{A}^{1})$
is a family of rational ramphoid cuspidal curves whose fiber over
![]() $0\in \mathbb{A}^{1}$
is a
$0\in \mathbb{A}^{1}$
is a
![]() $2/3$
-atom. Furthermore,
$2/3$
-atom. Furthermore,
![]() $\mathbb{G}_{m}$
acts on the base and total space of this family by
$\mathbb{G}_{m}$
acts on the base and total space of this family by
 $t\rightarrow \unicode[STIX]{x1D706}^{-1}t,c\rightarrow \unicode[STIX]{x1D706}c$
, since the subalgebra
$t\rightarrow \unicode[STIX]{x1D706}^{-1}t,c\rightarrow \unicode[STIX]{x1D706}c$
, since the subalgebra
 $\mathbb{C}[t^{2}+ct^{3},t^{5}]\subset \mathbb{C}[c,t]$
is invariant under this action. Thus, the family descends to
$\mathbb{C}[t^{2}+ct^{3},t^{5}]\subset \mathbb{C}[c,t]$
is invariant under this action. Thus, the family descends to
 $[\mathbb{A}^{1}/\mathbb{G}_{m}]$
and there is an induced map
$[\mathbb{A}^{1}/\mathbb{G}_{m}]$
and there is an induced map
 $[\mathbb{A}^{1}/\mathbb{G}_{m}]\rightarrow \overline{{\mathcal{M}}}_{2,1}(2/3)$
. This map is a locally closed immersion by [Reference van der WyckVdW10, Theorem 1.109], and the image is precisely
$[\mathbb{A}^{1}/\mathbb{G}_{m}]\rightarrow \overline{{\mathcal{M}}}_{2,1}(2/3)$
. This map is a locally closed immersion by [Reference van der WyckVdW10, Theorem 1.109], and the image is precisely
 $\overline{{\mathcal{S}}}_{2,1}(2/3)$
. Thus,
$\overline{{\mathcal{S}}}_{2,1}(2/3)$
. Thus,
 $\overline{{\mathcal{S}}}_{2,1}(2/3)\simeq [\mathbb{A}^{1}/\mathbb{G}_{m}]$
, as desired.◻
$\overline{{\mathcal{S}}}_{2,1}(2/3)\simeq [\mathbb{A}^{1}/\mathbb{G}_{m}]$
, as desired.◻
For higher values of
![]() $(g,n)$
, the key observation is that every curve in
$(g,n)$
, the key observation is that every curve in
 $\overline{{\mathcal{S}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
can be obtained from an
$\overline{{\mathcal{S}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
can be obtained from an
![]() $\unicode[STIX]{x1D6FC}_{c}$
-stable curve by ‘sprouting’ an appropriate singularity. We make this precise in the following definition.
$\unicode[STIX]{x1D6FC}_{c}$
-stable curve by ‘sprouting’ an appropriate singularity. We make this precise in the following definition.
Definition 4.4. If
![]() $(C,p_{1})$
is a one-pointed curve, we say that
$(C,p_{1})$
is a one-pointed curve, we say that
![]() $C^{\prime }$
is a (ramphoid) cuspidal sprouting of
$C^{\prime }$
is a (ramphoid) cuspidal sprouting of
![]() $(C,p_{1})$
if
$(C,p_{1})$
if
![]() $C^{\prime }$
contains a (ramphoid) cusp
$C^{\prime }$
contains a (ramphoid) cusp
![]() $q\in C^{\prime }$
, and the pointed normalization of
$q\in C^{\prime }$
, and the pointed normalization of
![]() $C^{\prime }$
at
$C^{\prime }$
at
![]() $q$
is isomorphic to one of:
$q$
is isomorphic to one of:
-
(a)
 $(C,p_{1})$
; or
$(C,p_{1})$
; or -
(b)
 $(C\cup \mathbb{P}^{1},\infty )$
, where
$(C\cup \mathbb{P}^{1},\infty )$
, where
 $C$
and
$C$
and
 $\mathbb{P}^{1}$
are glued nodally by identifying
$\mathbb{P}^{1}$
are glued nodally by identifying
 $p_{1}\sim 0$
.
$p_{1}\sim 0$
.
If
 $(C,p_{1},p_{2})$
is a two-pointed curve, we say that
$(C,p_{1},p_{2})$
is a two-pointed curve, we say that
![]() $C^{\prime }$
is a tacnodal sprouting of
$C^{\prime }$
is a tacnodal sprouting of
 $(C,p_{1},p_{2})$
if
$(C,p_{1},p_{2})$
if
![]() $C^{\prime }$
contains a tacnode
$C^{\prime }$
contains a tacnode
![]() $q\in C^{\prime }$
, and the pointed normalization of
$q\in C^{\prime }$
, and the pointed normalization of
![]() $C^{\prime }$
at
$C^{\prime }$
at
![]() $q$
is isomorphic to one of:
$q$
is isomorphic to one of:
-
(a)
 $(C,p_{1},p_{2})$
;
$(C,p_{1},p_{2})$
; -
(b)
 $(C\cup \mathbb{P}^{1},p_{1},\infty )$
, where
$(C\cup \mathbb{P}^{1},p_{1},\infty )$
, where
 $C$
and
$C$
and
 $\mathbb{P}^{1}$
are glued nodally by identifying
$\mathbb{P}^{1}$
are glued nodally by identifying
 $p_{2}\sim 0$
;
$p_{2}\sim 0$
; -
(c)
 $(C\cup \mathbb{P}^{1},p_{2},\infty )$
, where
$(C\cup \mathbb{P}^{1},p_{2},\infty )$
, where
 $C$
and
$C$
and
 $\mathbb{P}^{1}$
are glued nodally by identifying
$\mathbb{P}^{1}$
are glued nodally by identifying
 $p_{1}\sim 0$
; or
$p_{1}\sim 0$
; or -
(d)
 $(C\cup \mathbb{P}^{1}\cup \mathbb{P}^{1},\infty _{1},\infty _{2})$
, where
$(C\cup \mathbb{P}^{1}\cup \mathbb{P}^{1},\infty _{1},\infty _{2})$
, where
 $C$
is glued nodally to two copies of
$C$
is glued nodally to two copies of
 $\mathbb{P}^{1}$
along
$\mathbb{P}^{1}$
along
 $p_{1}\sim 0,p_{2}\sim 0$
.
$p_{1}\sim 0,p_{2}\sim 0$
.
In this definition, we allow the possibility that
 $(C,p_{1},p_{2})=(C_{1},p_{1})\coprod (C_{2},p_{2})$
is disconnected, with one marked point on each connected component.
$(C,p_{1},p_{2})=(C_{1},p_{1})\coprod (C_{2},p_{2})$
is disconnected, with one marked point on each connected component.
If
![]() $(C,p_{1})$
is a one-pointed curve, we say that
$(C,p_{1})$
is a one-pointed curve, we say that
![]() $C^{\prime }$
is a one-sided tacnodal sprouting of
$C^{\prime }$
is a one-sided tacnodal sprouting of
![]() $(C,p_{1})$
if
$(C,p_{1})$
if
![]() $C^{\prime }$
contains a tacnode
$C^{\prime }$
contains a tacnode
![]() $q\in C^{\prime }$
, and the pointed normalization of
$q\in C^{\prime }$
, and the pointed normalization of
![]() $C^{\prime }$
at
$C^{\prime }$
at
![]() $q$
is isomorphic to one of:
$q$
is isomorphic to one of:
-
(a)
 $(C,p_{1})\coprod (\mathbb{P}^{1},0)$
; or
$(C,p_{1})\coprod (\mathbb{P}^{1},0)$
; or -
(b)
 $(C\cup \mathbb{P}^{1},\infty )\coprod (\mathbb{P}^{1},0)$
, where
$(C\cup \mathbb{P}^{1},\infty )\coprod (\mathbb{P}^{1},0)$
, where
 $C$
and
$C$
and
 $\mathbb{P}^{1}$
are glued nodally by identifying
$\mathbb{P}^{1}$
are glued nodally by identifying
 $p_{1}\sim 0$
.
$p_{1}\sim 0$
.
Remark.
Suppose that
![]() $C^{\prime }$
is a cuspidal sprouting, one-sided tacnodal sprouting, or ramphoid cuspidal sprouting of
$C^{\prime }$
is a cuspidal sprouting, one-sided tacnodal sprouting, or ramphoid cuspidal sprouting of
![]() $(C,p_{1})$
(respectively, tacnodal sprouting of
$(C,p_{1})$
(respectively, tacnodal sprouting of
 $(C,p_{1},p_{2})$
) with
$(C,p_{1},p_{2})$
) with
![]() $\unicode[STIX]{x1D6FC}_{c}$
-critical singularity
$\unicode[STIX]{x1D6FC}_{c}$
-critical singularity
![]() $q\in C^{\prime }$
. Then
$q\in C^{\prime }$
. Then
![]() $(C,p_{1})$
(respectively,
$(C,p_{1})$
(respectively,
 $(C,p_{1},p_{2})$
) is the stable pointed normalization of
$(C,p_{1},p_{2})$
) is the stable pointed normalization of
![]() $C^{\prime }$
along
$C^{\prime }$
along
![]() $q$
. By Lemma 4.2,
$q$
. By Lemma 4.2,
![]() $C^{\prime }$
is
$C^{\prime }$
is
![]() $\unicode[STIX]{x1D6FC}_{c}$
-stable if and only if
$\unicode[STIX]{x1D6FC}_{c}$
-stable if and only if
![]() $(C,p_{1})$
(respectively,
$(C,p_{1})$
(respectively,
 $(C,p_{1},p_{2})$
) is
$(C,p_{1},p_{2})$
) is
![]() $\unicode[STIX]{x1D6FC}_{c}$
-stable.
$\unicode[STIX]{x1D6FC}_{c}$
-stable.
Lemma 4.5. Fix
 $\unicode[STIX]{x1D6FC}_{c}\in \{9/11,7/10,2/3\}$
and suppose that
$\unicode[STIX]{x1D6FC}_{c}\in \{9/11,7/10,2/3\}$
and suppose that
 $(C,\{p_{i}\}_{i=1}^{n})\in \overline{{\mathcal{S}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
.
$(C,\{p_{i}\}_{i=1}^{n})\in \overline{{\mathcal{S}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
.
-
(i) If
 $(g,n)\neq (1,1)$
, then
$(g,n)\neq (1,1)$
, then
 $(C,\{p_{i}\}_{i=1}^{n})$
is a cuspidal sprouting of a
$(C,\{p_{i}\}_{i=1}^{n})$
is a cuspidal sprouting of a
 $9/11$
-stable curve in
$9/11$
-stable curve in
 $\overline{{\mathcal{M}}}_{g-1,n+1}(9/11)$
.
$\overline{{\mathcal{M}}}_{g-1,n+1}(9/11)$
. -
(ii) If
 $(g,n)\neq (1,2)$
, then one of the following holds:
$(g,n)\neq (1,2)$
, then one of the following holds:-
(a)
 $(C,\{p_{i}\}_{i=1}^{n})$
is a tacnodal sprouting of a
$(C,\{p_{i}\}_{i=1}^{n})$
is a tacnodal sprouting of a
 $7/10$
-stable curve in
$7/10$
-stable curve in
 $\overline{{\mathcal{M}}}_{g-2,n+2}(7/10)$
;
$\overline{{\mathcal{M}}}_{g-2,n+2}(7/10)$
; -
(b)
 $(C,\{p_{i}\}_{i=1}^{n})$
is a tacnodal sprouting of a
$(C,\{p_{i}\}_{i=1}^{n})$
is a tacnodal sprouting of a
 $7/10$
-stable curve in
$7/10$
-stable curve in  $$\begin{eqnarray}\overline{{\mathcal{M}}}_{g-i-1,n-m+1}(7/10)\times \overline{{\mathcal{M}}}_{i,m+1}(7/10);\quad \text{or}\end{eqnarray}$$
$$\begin{eqnarray}\overline{{\mathcal{M}}}_{g-i-1,n-m+1}(7/10)\times \overline{{\mathcal{M}}}_{i,m+1}(7/10);\quad \text{or}\end{eqnarray}$$
-
(c)
 $(C,\{p_{i}\}_{i=1}^{n})$
is a one-sided tacnodal sprouting of a
$(C,\{p_{i}\}_{i=1}^{n})$
is a one-sided tacnodal sprouting of a
 $7/10$
-stable curve in
$7/10$
-stable curve in
 $\overline{{\mathcal{M}}}_{g-1,n}(7/10)$
.
$\overline{{\mathcal{M}}}_{g-1,n}(7/10)$
.
-
-
(iii) If
 $(g,n)\neq (2,1)$
, then
$(g,n)\neq (2,1)$
, then
 $(C,\{p_{i}\}_{i=1}^{n})$
is a ramphoid cuspidal sprouting of a
$(C,\{p_{i}\}_{i=1}^{n})$
is a ramphoid cuspidal sprouting of a
 $2/3$
-stable curve in
$2/3$
-stable curve in
 $\overline{{\mathcal{M}}}_{g-2,n+2}(2/3)$
.
$\overline{{\mathcal{M}}}_{g-2,n+2}(2/3)$
.
Proof. If
 $(C,\{p_{i}\}_{i=1}^{n})\in \overline{{\mathcal{S}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
, then
$(C,\{p_{i}\}_{i=1}^{n})\in \overline{{\mathcal{S}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
, then
 $(C,\{p_{i}\}_{i=1}^{n})$
contains an
$(C,\{p_{i}\}_{i=1}^{n})$
contains an
![]() $\unicode[STIX]{x1D6FC}_{c}$
-critical singularity
$\unicode[STIX]{x1D6FC}_{c}$
-critical singularity
![]() $q\in C$
. The stable pointed normalization of
$q\in C$
. The stable pointed normalization of
 $(C,\{p_{i}\}_{i=1}^{n})$
along
$(C,\{p_{i}\}_{i=1}^{n})$
along
![]() $q$
is well defined by our hypothesis on
$q$
is well defined by our hypothesis on
![]() $(g,n)$
, and is
$(g,n)$
, and is
![]() $\unicode[STIX]{x1D6FC}_{c}$
-stable by Lemma 4.2.◻
$\unicode[STIX]{x1D6FC}_{c}$
-stable by Lemma 4.2.◻
Lemma 4.5 gives a set-theoretic description of
 $\overline{{\mathcal{S}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
, and we must now augment this to a stack-theoretic description. This means constructing universal families of cuspidal, tacnodal, and ramphoid cuspidal sproutings. A nearly identical construction was carried out in [Reference SmythSmy11b] for elliptic
$\overline{{\mathcal{S}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
, and we must now augment this to a stack-theoretic description. This means constructing universal families of cuspidal, tacnodal, and ramphoid cuspidal sproutings. A nearly identical construction was carried out in [Reference SmythSmy11b] for elliptic
![]() $m$
-fold points (in particular, cusps and tacnodes) and for all curve singularities in [Reference van der WyckVdW10]. The only key difference is that here we allow all branches to sprout rational curves rather than a restricted subset. Therefore, we obtain non-separated, stacky compactifications (rather than Deligne–Mumford compactifications) of the associated crimping stack of the singularity. In what follows, if
$m$
-fold points (in particular, cusps and tacnodes) and for all curve singularities in [Reference van der WyckVdW10]. The only key difference is that here we allow all branches to sprout rational curves rather than a restricted subset. Therefore, we obtain non-separated, stacky compactifications (rather than Deligne–Mumford compactifications) of the associated crimping stack of the singularity. In what follows, if
![]() ${\mathcal{C}}\rightarrow T$
is any family of curves with a section
${\mathcal{C}}\rightarrow T$
is any family of curves with a section
![]() $\unicode[STIX]{x1D70F}$
, we say that
$\unicode[STIX]{x1D70F}$
, we say that
![]() ${\mathcal{C}}$
has an
${\mathcal{C}}$
has an
![]() $A_{k}$
-singularity along
$A_{k}$
-singularity along
![]() $\unicode[STIX]{x1D70F}$
if, étale locally on the base, the Henselization of
$\unicode[STIX]{x1D70F}$
if, étale locally on the base, the Henselization of
![]() ${\mathcal{C}}$
along
${\mathcal{C}}$
along
![]() $\unicode[STIX]{x1D70F}$
is isomorphic to the Henselization of
$\unicode[STIX]{x1D70F}$
is isomorphic to the Henselization of
 $T\times \mathbb{C}[x,y]/(y^{2}-x^{k+1})$
along the zero section (cf. [Reference van der WyckVdW10, Definition 1.64]).
$T\times \mathbb{C}[x,y]/(y^{2}-x^{k+1})$
along the zero section (cf. [Reference van der WyckVdW10, Definition 1.64]).
Definition 4.6. Let
 $\operatorname{Sprout}_{g,n}(A_{k})$
denote the stack of flat families of curves
$\operatorname{Sprout}_{g,n}(A_{k})$
denote the stack of flat families of curves
 $({\mathcal{C}}\rightarrow T,\{\unicode[STIX]{x1D70E}_{i}\}_{i=1}^{n+1})$
satisfying:
$({\mathcal{C}}\rightarrow T,\{\unicode[STIX]{x1D70E}_{i}\}_{i=1}^{n+1})$
satisfying:
-
(i)
 $({\mathcal{C}}\rightarrow T,\{\unicode[STIX]{x1D70E}_{i}\}_{i=1}^{n})$
is a
$({\mathcal{C}}\rightarrow T,\{\unicode[STIX]{x1D70E}_{i}\}_{i=1}^{n})$
is a
 $T$
-point of
$T$
-point of
 ${\mathcal{U}}_{g,n}(A_{k})$
; and
${\mathcal{U}}_{g,n}(A_{k})$
; and -
(ii)
 ${\mathcal{C}}$
has an
${\mathcal{C}}$
has an
 $A_{k}$
-singularity along
$A_{k}$
-singularity along
 $\unicode[STIX]{x1D70E}_{n+1}$
.
$\unicode[STIX]{x1D70E}_{n+1}$
.
The fact that
 $\operatorname{Sprout}_{g,n}(A_{k})$
is an algebraic stack over
$\operatorname{Sprout}_{g,n}(A_{k})$
is an algebraic stack over
 $(\text{Schemes}/\mathbb{C})$
is verified in [Reference van der WyckVdW10]. There are obvious forgetful functors
$(\text{Schemes}/\mathbb{C})$
is verified in [Reference van der WyckVdW10]. There are obvious forgetful functors
 $$\begin{eqnarray}F_{k}:\operatorname{Sprout}_{g,n}(A_{k})\rightarrow {\mathcal{U}}_{g,n}(A_{k}),\end{eqnarray}$$
$$\begin{eqnarray}F_{k}:\operatorname{Sprout}_{g,n}(A_{k})\rightarrow {\mathcal{U}}_{g,n}(A_{k}),\end{eqnarray}$$
given by forgetting the section
![]() $\unicode[STIX]{x1D70E}_{n+1}$
.
$\unicode[STIX]{x1D70E}_{n+1}$
.
Proposition 4.7.
![]() $F_{k}$
is representable and finite.
$F_{k}$
is representable and finite.
Proof. It is clear that
![]() $F_{k}$
is representable. The fact that
$F_{k}$
is representable. The fact that
![]() $F_{k}$
is quasi-finite follows from the observations that a curve
$F_{k}$
is quasi-finite follows from the observations that a curve
 $(C,\{p_{i}\}_{i=1}^{n})$
in
$(C,\{p_{i}\}_{i=1}^{n})$
in
 ${\mathcal{U}}_{g,n}(A_{k})$
has only a finite number of
${\mathcal{U}}_{g,n}(A_{k})$
has only a finite number of
![]() $A_{k}$
-singularities and that for a
$A_{k}$
-singularities and that for a
![]() $\mathbb{C}$
-point
$\mathbb{C}$
-point
 $x\in \operatorname{Sprout}_{g,n}(A_{k})$
, the induced map
$x\in \operatorname{Sprout}_{g,n}(A_{k})$
, the induced map
 $\operatorname{Aut}_{\operatorname{Sprout}_{g,n}(A_{k})}(x)\rightarrow \operatorname{Aut}_{{\mathcal{U}}_{g,n}(A_{k})}(F_{k}(x))$
on automorphism groups has finite cokernel. To show that
$\operatorname{Aut}_{\operatorname{Sprout}_{g,n}(A_{k})}(x)\rightarrow \operatorname{Aut}_{{\mathcal{U}}_{g,n}(A_{k})}(F_{k}(x))$
on automorphism groups has finite cokernel. To show that
![]() $F_{k}$
is finite, it now suffices to verify the valuative criterion for properness: let
$F_{k}$
is finite, it now suffices to verify the valuative criterion for properness: let
![]() $\unicode[STIX]{x1D6E5}$
be the spectrum of a discrete valuation ring, let
$\unicode[STIX]{x1D6E5}$
be the spectrum of a discrete valuation ring, let
![]() $\unicode[STIX]{x1D6E5}^{\ast }$
denote the spectrum of its fraction field, and suppose that we are given a diagram
$\unicode[STIX]{x1D6E5}^{\ast }$
denote the spectrum of its fraction field, and suppose that we are given a diagram

This corresponds to a diagram of families,

such that
![]() ${\mathcal{C}}_{\unicode[STIX]{x1D6E5}^{\ast }}$
has an
${\mathcal{C}}_{\unicode[STIX]{x1D6E5}^{\ast }}$
has an
![]() $A_{k}$
-singularity along
$A_{k}$
-singularity along
![]() $\unicode[STIX]{x1D70E}_{n+1}$
. Since
$\unicode[STIX]{x1D70E}_{n+1}$
. Since
![]() ${\mathcal{C}}\rightarrow \unicode[STIX]{x1D6E5}$
is proper,
${\mathcal{C}}\rightarrow \unicode[STIX]{x1D6E5}$
is proper,
![]() $\unicode[STIX]{x1D70E}_{n+1}$
extends uniquely to a section of
$\unicode[STIX]{x1D70E}_{n+1}$
extends uniquely to a section of
![]() $\unicode[STIX]{x1D70B}$
and, since the limit of an
$\unicode[STIX]{x1D70B}$
and, since the limit of an
![]() $A_{k}$
-singularity in
$A_{k}$
-singularity in
 ${\mathcal{U}}_{g,n}(A_{k})$
is necessarily an
${\mathcal{U}}_{g,n}(A_{k})$
is necessarily an
![]() $A_{k}$
-singularity,
$A_{k}$
-singularity,
![]() ${\mathcal{C}}$
has an
${\mathcal{C}}$
has an
![]() $A_{k}$
-singularity along
$A_{k}$
-singularity along
![]() $\unicode[STIX]{x1D70E}_{n+1}$
. This induces a unique lift
$\unicode[STIX]{x1D70E}_{n+1}$
. This induces a unique lift
 $\unicode[STIX]{x1D6E5}\rightarrow \operatorname{Sprout}_{g,n}(A_{k})$
; cf. [Reference van der WyckVdW10, Theorem 1.109].◻
$\unicode[STIX]{x1D6E5}\rightarrow \operatorname{Sprout}_{g,n}(A_{k})$
; cf. [Reference van der WyckVdW10, Theorem 1.109].◻
The algebraic stacks
 $\operatorname{Sprout}_{g,n}(A_{k})$
also admit stable pointed normalization functors, given by forgetting the crimping data of the singularity along
$\operatorname{Sprout}_{g,n}(A_{k})$
also admit stable pointed normalization functors, given by forgetting the crimping data of the singularity along
![]() $\unicode[STIX]{x1D70E}_{n+1}$
. To be precise, if
$\unicode[STIX]{x1D70E}_{n+1}$
. To be precise, if
 $({\mathcal{C}}\rightarrow T,\{\unicode[STIX]{x1D70E}\}_{i=1}^{n+1})$
is a
$({\mathcal{C}}\rightarrow T,\{\unicode[STIX]{x1D70E}\}_{i=1}^{n+1})$
is a
![]() $T$
-point of
$T$
-point of
 $\operatorname{Sprout}_{g,n}(A_{k})$
, there exists a commutative diagram
$\operatorname{Sprout}_{g,n}(A_{k})$
, there exists a commutative diagram

satisfying:
-
(i)
 $(\widetilde{{\mathcal{C}}}\rightarrow T,\{\tilde{\unicode[STIX]{x1D70E}}_{i}\}_{i=1}^{n+\bar{k}})$
is a family of
$(\widetilde{{\mathcal{C}}}\rightarrow T,\{\tilde{\unicode[STIX]{x1D70E}}_{i}\}_{i=1}^{n+\bar{k}})$
is a family of
 $(n+\bar{k})$
-pointed curves, where
$(n+\bar{k})$
-pointed curves, where
 $\bar{k}\in \{1,2\}$
;
$\bar{k}\in \{1,2\}$
; -
(ii)
 $\unicode[STIX]{x1D713}$
is the pointed normalization of
$\unicode[STIX]{x1D713}$
is the pointed normalization of
 ${\mathcal{C}}$
along
${\mathcal{C}}$
along
 $\unicode[STIX]{x1D70E}_{n+1}$
, i.e.
$\unicode[STIX]{x1D70E}_{n+1}$
, i.e.
 $\unicode[STIX]{x1D713}$
is finite and restricts to an isomorphism on the open set
$\unicode[STIX]{x1D713}$
is finite and restricts to an isomorphism on the open set
 $\widetilde{{\mathcal{C}}}-\bigcup _{i=1}^{\bar{k}}\tilde{\unicode[STIX]{x1D70E}}_{n+i}$
; and
$\widetilde{{\mathcal{C}}}-\bigcup _{i=1}^{\bar{k}}\tilde{\unicode[STIX]{x1D70E}}_{n+i}$
; and -
(iii)
 $\unicode[STIX]{x1D719}$
is the stabilization of
$\unicode[STIX]{x1D719}$
is the stabilization of
 $(\widetilde{{\mathcal{C}}},\{\tilde{\unicode[STIX]{x1D70E}}_{i}\}_{i=1}^{n+\bar{k}})$
, i.e.
$(\widetilde{{\mathcal{C}}},\{\tilde{\unicode[STIX]{x1D70E}}_{i}\}_{i=1}^{n+\bar{k}})$
, i.e.
 $\unicode[STIX]{x1D719}$
is the morphism associated to a high multiple of the line bundle
$\unicode[STIX]{x1D719}$
is the morphism associated to a high multiple of the line bundle
 $\unicode[STIX]{x1D714}_{\widetilde{{\mathcal{C}}}/T}(\unicode[STIX]{x1D6F4}_{i=1}^{n+\bar{k}}\tilde{\unicode[STIX]{x1D70E}}_{i})$
.
$\unicode[STIX]{x1D714}_{\widetilde{{\mathcal{C}}}/T}(\unicode[STIX]{x1D6F4}_{i=1}^{n+\bar{k}}\tilde{\unicode[STIX]{x1D70E}}_{i})$
.
Remark 4.8. Issues arise when defining the stable pointed normalization for
![]() $(g,n)$
small relative to
$(g,n)$
small relative to
![]() $k$
. From now on, we assume that
$k$
. From now on, we assume that
 $k\in \{2,3,4\}$
, and that
$k\in \{2,3,4\}$
, and that
 $(g,n)\neq (1,1),(1,2),(2,1)$
when
$(g,n)\neq (1,1),(1,2),(2,1)$
when
 $k=2,3,4$
, respectively. This ensures that the stabilization morphism
$k=2,3,4$
, respectively. This ensures that the stabilization morphism
![]() $\unicode[STIX]{x1D719}$
is well defined. Indeed, under these hypotheses,
$\unicode[STIX]{x1D719}$
is well defined. Indeed, under these hypotheses,
 $\unicode[STIX]{x1D714}_{\widetilde{{\mathcal{C}}}}(\unicode[STIX]{x1D6F4}_{i}\tilde{\unicode[STIX]{x1D70E}}_{i})$
will be relatively big and nef, and the only components of fibers of
$\unicode[STIX]{x1D714}_{\widetilde{{\mathcal{C}}}}(\unicode[STIX]{x1D6F4}_{i}\tilde{\unicode[STIX]{x1D70E}}_{i})$
will be relatively big and nef, and the only components of fibers of
 $(\widetilde{{\mathcal{C}}},\{\tilde{\unicode[STIX]{x1D70E}}_{i}\}_{i=1}^{n+\bar{k}})$
on which
$(\widetilde{{\mathcal{C}}},\{\tilde{\unicode[STIX]{x1D70E}}_{i}\}_{i=1}^{n+\bar{k}})$
on which
 $\unicode[STIX]{x1D714}_{\widetilde{{\mathcal{C}}}}(\unicode[STIX]{x1D6F4}_{i}\tilde{\unicode[STIX]{x1D70E}}_{i})$
has degree zero will be the rational curves that meet the rest of the curve in a single node and are marked by one of the sections
$\unicode[STIX]{x1D714}_{\widetilde{{\mathcal{C}}}}(\unicode[STIX]{x1D6F4}_{i}\tilde{\unicode[STIX]{x1D70E}}_{i})$
has degree zero will be the rational curves that meet the rest of the curve in a single node and are marked by one of the sections
 $\{\tilde{\unicode[STIX]{x1D70E}}_{n+i}\}_{i=1}^{\bar{k}}$
. The effect of
$\{\tilde{\unicode[STIX]{x1D70E}}_{n+i}\}_{i=1}^{\bar{k}}$
. The effect of
![]() $\unicode[STIX]{x1D719}$
is simply to blow down these rational curves.
$\unicode[STIX]{x1D719}$
is simply to blow down these rational curves.
Since normalization and stabilization are canonically defined, the association
 $$\begin{eqnarray}({\mathcal{C}}\rightarrow T,\{\unicode[STIX]{x1D70E}_{i}\}_{i=1}^{n})\mapsto ({\mathcal{C}}^{s}\rightarrow T,\{\unicode[STIX]{x1D70E}_{i}^{s}\}_{i=1}^{n+\bar{k}})\end{eqnarray}$$
$$\begin{eqnarray}({\mathcal{C}}\rightarrow T,\{\unicode[STIX]{x1D70E}_{i}\}_{i=1}^{n})\mapsto ({\mathcal{C}}^{s}\rightarrow T,\{\unicode[STIX]{x1D70E}_{i}^{s}\}_{i=1}^{n+\bar{k}})\end{eqnarray}$$
is functorial, and we obtain normalization functors:
 $$\begin{eqnarray}\displaystyle N_{2}:\operatorname{Sprout}_{g,n}(A_{2}) & \rightarrow & \displaystyle {\mathcal{U}}_{g-1,n+1}(A_{2}),\nonumber\\ \displaystyle N_{3}:\operatorname{Sprout}_{g,n}(A_{3}) & \rightarrow & \displaystyle \coprod _{\substack{ g_{1}+g_{2}=g \\ n_{1}+n_{2}=n}}({\mathcal{U}}_{g_{1},n_{1}+1}(A_{3})\times {\mathcal{U}}_{g_{2},n_{2}+1}(A_{3}))\coprod {\mathcal{U}}_{g-2,n+2}(A_{3})\coprod {\mathcal{U}}_{g-1,n+1}(A_{3}),\nonumber\\ \displaystyle N_{4}:\operatorname{Sprout}_{g,n}(A_{4}) & \rightarrow & \displaystyle {\mathcal{U}}_{g-2,n+1}(A_{4}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N_{2}:\operatorname{Sprout}_{g,n}(A_{2}) & \rightarrow & \displaystyle {\mathcal{U}}_{g-1,n+1}(A_{2}),\nonumber\\ \displaystyle N_{3}:\operatorname{Sprout}_{g,n}(A_{3}) & \rightarrow & \displaystyle \coprod _{\substack{ g_{1}+g_{2}=g \\ n_{1}+n_{2}=n}}({\mathcal{U}}_{g_{1},n_{1}+1}(A_{3})\times {\mathcal{U}}_{g_{2},n_{2}+1}(A_{3}))\coprod {\mathcal{U}}_{g-2,n+2}(A_{3})\coprod {\mathcal{U}}_{g-1,n+1}(A_{3}),\nonumber\\ \displaystyle N_{4}:\operatorname{Sprout}_{g,n}(A_{4}) & \rightarrow & \displaystyle {\mathcal{U}}_{g-2,n+1}(A_{4}).\nonumber\end{eqnarray}$$
The connected components of the range of
![]() $N_{3}$
correspond to the different possibilities for the stable pointed normalization of
$N_{3}$
correspond to the different possibilities for the stable pointed normalization of
![]() ${\mathcal{C}}$
along
${\mathcal{C}}$
along
![]() $\unicode[STIX]{x1D70E}_{n+1}$
. Note that the last case
$\unicode[STIX]{x1D70E}_{n+1}$
. Note that the last case
 ${\mathcal{U}}_{g-1,n+1}(A_{3})$
corresponds to a one-sided tacnodal sprouting, i.e. one connected component of the pointed normalization of
${\mathcal{U}}_{g-1,n+1}(A_{3})$
corresponds to a one-sided tacnodal sprouting, i.e. one connected component of the pointed normalization of
![]() ${\mathcal{C}}$
along
${\mathcal{C}}$
along
![]() $\unicode[STIX]{x1D70E}_{n+1}$
is a family of two-pointed irreducible rational curves. It is convenient to distinguish these possibilities by defining
$\unicode[STIX]{x1D70E}_{n+1}$
is a family of two-pointed irreducible rational curves. It is convenient to distinguish these possibilities by defining
 $$\begin{eqnarray}\displaystyle \operatorname{Sprout}_{g,n}^{ns}(A_{3}) & = & \displaystyle N_{3}^{-1}({\mathcal{U}}_{g-2,n+2}(A_{3})),\nonumber\\ \displaystyle \operatorname{Sprout}_{g,n}^{g_{1},n_{1}}(A_{3}) & = & \displaystyle N_{3}^{-1}({\mathcal{U}}_{g_{1},n_{1}+1}(A_{3})\times {\mathcal{U}}_{g_{2},n_{2}+1}(A_{3})),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Sprout}_{g,n}^{ns}(A_{3}) & = & \displaystyle N_{3}^{-1}({\mathcal{U}}_{g-2,n+2}(A_{3})),\nonumber\\ \displaystyle \operatorname{Sprout}_{g,n}^{g_{1},n_{1}}(A_{3}) & = & \displaystyle N_{3}^{-1}({\mathcal{U}}_{g_{1},n_{1}+1}(A_{3})\times {\mathcal{U}}_{g_{2},n_{2}+1}(A_{3})),\nonumber\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle \operatorname{Sprout}_{g,n}^{0,2}(A_{3}) & = & \displaystyle N_{3}^{-1}({\mathcal{U}}_{g-1,n+1}(A_{3})).\hspace{64.79993pt}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Sprout}_{g,n}^{0,2}(A_{3}) & = & \displaystyle N_{3}^{-1}({\mathcal{U}}_{g-1,n+1}(A_{3})).\hspace{64.79993pt}\nonumber\end{eqnarray}$$
The following key proposition shows that
![]() $N_{k}$
makes
$N_{k}$
makes
 $\operatorname{Sprout}_{g,n}(A_{k})$
a stacky projective bundle over the moduli stack of pointed normalizations.
$\operatorname{Sprout}_{g,n}(A_{k})$
a stacky projective bundle over the moduli stack of pointed normalizations.
We will use the following notation: if
![]() ${\mathcal{E}}$
is a locally free sheaf on an algebraic stack
${\mathcal{E}}$
is a locally free sheaf on an algebraic stack
![]() ${\mathcal{X}}$
, we let
${\mathcal{X}}$
, we let
![]() $V({\mathcal{E}})$
denote the total space of the associated vector bundle,
$V({\mathcal{E}})$
denote the total space of the associated vector bundle,
 $[V({\mathcal{E}})/\mathbb{G}_{m}]$
the quotient stack for the natural action of
$[V({\mathcal{E}})/\mathbb{G}_{m}]$
the quotient stack for the natural action of
![]() $\mathbb{G}_{m}$
on the fibers of
$\mathbb{G}_{m}$
on the fibers of
![]() $V({\mathcal{E}})$
, and
$V({\mathcal{E}})$
, and
 $p:[V({\mathcal{E}})/\mathbb{G}_{m}]\rightarrow T$
the natural projection.
$p:[V({\mathcal{E}})/\mathbb{G}_{m}]\rightarrow T$
the natural projection.
Proposition 4.9. In the following statements, we let
 $(\unicode[STIX]{x1D70B}:{\mathcal{C}}\rightarrow {\mathcal{U}}_{g,n}(A_{k}),\{\unicode[STIX]{x1D70E}_{i}\}_{i=1}^{n})$
denote the universal family over
$(\unicode[STIX]{x1D70B}:{\mathcal{C}}\rightarrow {\mathcal{U}}_{g,n}(A_{k}),\{\unicode[STIX]{x1D70E}_{i}\}_{i=1}^{n})$
denote the universal family over
 ${\mathcal{U}}_{g,n}(A_{k})$
, and
${\mathcal{U}}_{g,n}(A_{k})$
, and
 $(\unicode[STIX]{x1D70B}:{\mathcal{C}}\rightarrow {\mathcal{U}}_{g_{1},n_{1}}(A_{k})\times {\mathcal{U}}_{g_{2},n_{2}}(A_{k}),\{\unicode[STIX]{x1D70E}_{i}\}_{i=1}^{n_{1}},\{\unicode[STIX]{x1D70F}_{i}\}_{i=1}^{n_{2}})$
the universal family over
$(\unicode[STIX]{x1D70B}:{\mathcal{C}}\rightarrow {\mathcal{U}}_{g_{1},n_{1}}(A_{k})\times {\mathcal{U}}_{g_{2},n_{2}}(A_{k}),\{\unicode[STIX]{x1D70E}_{i}\}_{i=1}^{n_{1}},\{\unicode[STIX]{x1D70F}_{i}\}_{i=1}^{n_{2}})$
the universal family over
 ${\mathcal{U}}_{g_{1},n_{1}}(A_{k})\times {\mathcal{U}}_{g_{2},n_{2}}(A_{k})$
.
${\mathcal{U}}_{g_{1},n_{1}}(A_{k})\times {\mathcal{U}}_{g_{2},n_{2}}(A_{k})$
.
-
(i) Let
 ${\mathcal{E}}$
be the invertible sheaf on
${\mathcal{E}}$
be the invertible sheaf on
 ${\mathcal{U}}_{g-1,n+1}(A_{2})$
defined by Then there exists an isomorphism
${\mathcal{U}}_{g-1,n+1}(A_{2})$
defined by Then there exists an isomorphism $$\begin{eqnarray}{\mathcal{E}}:=\unicode[STIX]{x1D70B}_{\ast }({\mathcal{O}}_{{\mathcal{C}}}(-2\unicode[STIX]{x1D70E}_{n+1})/{\mathcal{O}}_{{\mathcal{C}}}(-3\unicode[STIX]{x1D70E}_{n+1})).\end{eqnarray}$$
such that
$$\begin{eqnarray}{\mathcal{E}}:=\unicode[STIX]{x1D70B}_{\ast }({\mathcal{O}}_{{\mathcal{C}}}(-2\unicode[STIX]{x1D70E}_{n+1})/{\mathcal{O}}_{{\mathcal{C}}}(-3\unicode[STIX]{x1D70E}_{n+1})).\end{eqnarray}$$
such that $$\begin{eqnarray}\unicode[STIX]{x1D6FE}:[V({\mathcal{E}})/\mathbb{G}_{m}]\simeq \operatorname{Sprout}_{g,n}(A_{2})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}:[V({\mathcal{E}})/\mathbb{G}_{m}]\simeq \operatorname{Sprout}_{g,n}(A_{2})\end{eqnarray}$$
 $N_{2}\circ \unicode[STIX]{x1D6FE}=p$
.
$N_{2}\circ \unicode[STIX]{x1D6FE}=p$
.
-
(ii) Let
 ${\mathcal{E}}$
be the locally free sheaf on
${\mathcal{E}}$
be the locally free sheaf on
 ${\mathcal{U}}_{g-2,n+2}(A_{3})$
defined by Then there exists an isomorphism
${\mathcal{U}}_{g-2,n+2}(A_{3})$
defined by Then there exists an isomorphism $$\begin{eqnarray}{\mathcal{E}}:=\unicode[STIX]{x1D70B}_{\ast }({\mathcal{O}}_{{\mathcal{C}}}(-\unicode[STIX]{x1D70E}_{n+1})/{\mathcal{O}}_{{\mathcal{C}}}(-2\unicode[STIX]{x1D70E}_{n+1})\oplus {\mathcal{O}}_{{\mathcal{C}}}(-\unicode[STIX]{x1D70E}_{n+2})/{\mathcal{O}}_{{\mathcal{C}}}(-2\unicode[STIX]{x1D70E}_{n+2})).\end{eqnarray}$$
such that
$$\begin{eqnarray}{\mathcal{E}}:=\unicode[STIX]{x1D70B}_{\ast }({\mathcal{O}}_{{\mathcal{C}}}(-\unicode[STIX]{x1D70E}_{n+1})/{\mathcal{O}}_{{\mathcal{C}}}(-2\unicode[STIX]{x1D70E}_{n+1})\oplus {\mathcal{O}}_{{\mathcal{C}}}(-\unicode[STIX]{x1D70E}_{n+2})/{\mathcal{O}}_{{\mathcal{C}}}(-2\unicode[STIX]{x1D70E}_{n+2})).\end{eqnarray}$$
such that $$\begin{eqnarray}\unicode[STIX]{x1D6FE}:[V({\mathcal{E}})/\mathbb{G}_{m}]\simeq \operatorname{Sprout}_{g,n}^{ns}(A_{3})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}:[V({\mathcal{E}})/\mathbb{G}_{m}]\simeq \operatorname{Sprout}_{g,n}^{ns}(A_{3})\end{eqnarray}$$
 $N_{3}\circ \unicode[STIX]{x1D6FE}=p$
.
$N_{3}\circ \unicode[STIX]{x1D6FE}=p$
.
-
(iii) Let
 ${\mathcal{E}}$
be the locally free sheaf on
${\mathcal{E}}$
be the locally free sheaf on
 ${\mathcal{U}}_{g_{1},n_{1}+1}(A_{3})\times {\mathcal{U}}_{g_{2},n_{1}+1}(A_{3})$
defined by Then there exists an isomorphism
${\mathcal{U}}_{g_{1},n_{1}+1}(A_{3})\times {\mathcal{U}}_{g_{2},n_{1}+1}(A_{3})$
defined by Then there exists an isomorphism $$\begin{eqnarray}{\mathcal{E}}:=\unicode[STIX]{x1D70B}_{\ast }({\mathcal{O}}_{{\mathcal{C}}}(-\unicode[STIX]{x1D70E}_{n_{1}+1})/{\mathcal{O}}_{{\mathcal{C}}}(-2\unicode[STIX]{x1D70E}_{n_{1}+1})\oplus {\mathcal{O}}_{{\mathcal{C}}}(-\unicode[STIX]{x1D70F}_{n_{2}+1})/{\mathcal{O}}_{{\mathcal{C}}}(-2\unicode[STIX]{x1D70F}_{n_{2}+1})).\end{eqnarray}$$
such that
$$\begin{eqnarray}{\mathcal{E}}:=\unicode[STIX]{x1D70B}_{\ast }({\mathcal{O}}_{{\mathcal{C}}}(-\unicode[STIX]{x1D70E}_{n_{1}+1})/{\mathcal{O}}_{{\mathcal{C}}}(-2\unicode[STIX]{x1D70E}_{n_{1}+1})\oplus {\mathcal{O}}_{{\mathcal{C}}}(-\unicode[STIX]{x1D70F}_{n_{2}+1})/{\mathcal{O}}_{{\mathcal{C}}}(-2\unicode[STIX]{x1D70F}_{n_{2}+1})).\end{eqnarray}$$
such that $$\begin{eqnarray}\unicode[STIX]{x1D6FE}:[V({\mathcal{E}})/\mathbb{G}_{m}]\simeq \operatorname{Sprout}_{g,n}^{g_{1},n_{1}}(A_{3})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}:[V({\mathcal{E}})/\mathbb{G}_{m}]\simeq \operatorname{Sprout}_{g,n}^{g_{1},n_{1}}(A_{3})\end{eqnarray}$$
 $N_{3}\circ \unicode[STIX]{x1D6FE}=p$
.
$N_{3}\circ \unicode[STIX]{x1D6FE}=p$
.
-
(iv) Let
 ${\mathcal{E}}$
be the locally free sheaf on
${\mathcal{E}}$
be the locally free sheaf on
 ${\mathcal{U}}_{g-1,n+1}(A_{3})$
defined by Then there exists an isomorphism
${\mathcal{U}}_{g-1,n+1}(A_{3})$
defined by Then there exists an isomorphism $$\begin{eqnarray}{\mathcal{E}}:=\unicode[STIX]{x1D70B}_{\ast }({\mathcal{O}}_{{\mathcal{C}}}(-\unicode[STIX]{x1D70E}_{n+1})/{\mathcal{O}}_{{\mathcal{C}}}(-2\unicode[STIX]{x1D70E}_{n+1})).\end{eqnarray}$$
such that
$$\begin{eqnarray}{\mathcal{E}}:=\unicode[STIX]{x1D70B}_{\ast }({\mathcal{O}}_{{\mathcal{C}}}(-\unicode[STIX]{x1D70E}_{n+1})/{\mathcal{O}}_{{\mathcal{C}}}(-2\unicode[STIX]{x1D70E}_{n+1})).\end{eqnarray}$$
such that $$\begin{eqnarray}\unicode[STIX]{x1D6FE}:[V({\mathcal{E}})/\mathbb{G}_{m}]\simeq \operatorname{Sprout}_{g,n}^{0,2}(A_{3})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}:[V({\mathcal{E}})/\mathbb{G}_{m}]\simeq \operatorname{Sprout}_{g,n}^{0,2}(A_{3})\end{eqnarray}$$
 $N_{3}\circ \unicode[STIX]{x1D6FE}=p$
.
$N_{3}\circ \unicode[STIX]{x1D6FE}=p$
.
-
(v) Let
 ${\mathcal{E}}$
be the locally free sheaf on
${\mathcal{E}}$
be the locally free sheaf on
 ${\mathcal{U}}_{g-2,n+1}(A_{4})$
defined by Then there exists an isomorphism
${\mathcal{U}}_{g-2,n+1}(A_{4})$
defined by Then there exists an isomorphism $$\begin{eqnarray}{\mathcal{E}}:=\unicode[STIX]{x1D70B}_{\ast }({\mathcal{O}}_{{\mathcal{C}}}(-2\unicode[STIX]{x1D70E}_{n+1})/{\mathcal{O}}_{{\mathcal{C}}}(-4\unicode[STIX]{x1D70E}_{n+1})).\end{eqnarray}$$
such that
$$\begin{eqnarray}{\mathcal{E}}:=\unicode[STIX]{x1D70B}_{\ast }({\mathcal{O}}_{{\mathcal{C}}}(-2\unicode[STIX]{x1D70E}_{n+1})/{\mathcal{O}}_{{\mathcal{C}}}(-4\unicode[STIX]{x1D70E}_{n+1})).\end{eqnarray}$$
such that $$\begin{eqnarray}\unicode[STIX]{x1D6FE}:[V({\mathcal{E}})/\mathbb{G}_{m}]\simeq \operatorname{Sprout}_{g,n}(A_{4})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}:[V({\mathcal{E}})/\mathbb{G}_{m}]\simeq \operatorname{Sprout}_{g,n}(A_{4})\end{eqnarray}$$
 $N_{4}\circ \unicode[STIX]{x1D6FE}=p$
.
$N_{4}\circ \unicode[STIX]{x1D6FE}=p$
.
Proof. We prove the hardest case (v), and leave the others as an exercise to the reader. To construct a map
 $\unicode[STIX]{x1D6FE}:[V({\mathcal{E}})/\mathbb{G}_{m}]\rightarrow \operatorname{Sprout}_{g,n}(A_{4})$
, we start with a family
$\unicode[STIX]{x1D6FE}:[V({\mathcal{E}})/\mathbb{G}_{m}]\rightarrow \operatorname{Sprout}_{g,n}(A_{4})$
, we start with a family
 $(\unicode[STIX]{x1D70B}:{\mathcal{C}}\rightarrow X,\{\unicode[STIX]{x1D70E}_{i}\}_{i=1}^{n+1})$
in
$(\unicode[STIX]{x1D70B}:{\mathcal{C}}\rightarrow X,\{\unicode[STIX]{x1D70E}_{i}\}_{i=1}^{n+1})$
in
 ${\mathcal{U}}_{g-2,n+1}(A_{4})$
, and construct a family of ramphoid cuspidal sproutings over
${\mathcal{U}}_{g-2,n+1}(A_{4})$
, and construct a family of ramphoid cuspidal sproutings over
 $[V({\mathcal{E}}_{X})/\mathbb{G}_{m}]$
, where
$[V({\mathcal{E}}_{X})/\mathbb{G}_{m}]$
, where
 $$\begin{eqnarray}{\mathcal{E}}_{X}:=\unicode[STIX]{x1D70B}_{\ast }({\mathcal{O}}_{{\mathcal{C}}}(-2\unicode[STIX]{x1D70E}_{n+1})/{\mathcal{O}}_{{\mathcal{C}}}(-4\unicode[STIX]{x1D70E}_{n+1})).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{E}}_{X}:=\unicode[STIX]{x1D70B}_{\ast }({\mathcal{O}}_{{\mathcal{C}}}(-2\unicode[STIX]{x1D70E}_{n+1})/{\mathcal{O}}_{{\mathcal{C}}}(-4\unicode[STIX]{x1D70E}_{n+1})).\end{eqnarray}$$
Let
 $V:=V({\mathcal{E}}_{X})$
,
$V:=V({\mathcal{E}}_{X})$
,
 $p:V\rightarrow X$
the natural projection, and
$p:V\rightarrow X$
the natural projection, and
 $({\mathcal{C}}_{V}\rightarrow V,\unicode[STIX]{x1D70E}_{V})$
the family obtained from
$({\mathcal{C}}_{V}\rightarrow V,\unicode[STIX]{x1D70E}_{V})$
the family obtained from
 $({\mathcal{C}}\rightarrow X,\unicode[STIX]{x1D70E}_{n+1})$
by base change along
$({\mathcal{C}}\rightarrow X,\unicode[STIX]{x1D70E}_{n+1})$
by base change along
![]() $p$
. As the construction is local around
$p$
. As the construction is local around
![]() $\unicode[STIX]{x1D70E}_{n+1}$
, we will not keep track of
$\unicode[STIX]{x1D70E}_{n+1}$
, we will not keep track of
![]() $\{\unicode[STIX]{x1D70E}_{i}\}_{i=1}^{n}$
for the remainder of the argument. If we set
$\{\unicode[STIX]{x1D70E}_{i}\}_{i=1}^{n}$
for the remainder of the argument. If we set
 ${\mathcal{E}}_{V}=p^{\ast }{\mathcal{E}}_{X}$
, there existsa tautological section
${\mathcal{E}}_{V}=p^{\ast }{\mathcal{E}}_{X}$
, there existsa tautological section
 $e:{\mathcal{O}}_{V}\rightarrow {\mathcal{E}}_{V}$
. Let
$e:{\mathcal{O}}_{V}\rightarrow {\mathcal{E}}_{V}$
. Let
![]() $Z\subset V$
denote the divisor along which the composition
$Z\subset V$
denote the divisor along which the composition
 $$\begin{eqnarray}{\mathcal{O}}_{V}\rightarrow {\mathcal{E}}_{V}\rightarrow (\unicode[STIX]{x1D70B}_{V})_{\ast }({\mathcal{O}}_{{\mathcal{C}}_{V}}(-2\unicode[STIX]{x1D70E}_{V})/{\mathcal{O}}_{{\mathcal{C}}_{V}}(-3\unicode[STIX]{x1D70E}_{V}))\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{O}}_{V}\rightarrow {\mathcal{E}}_{V}\rightarrow (\unicode[STIX]{x1D70B}_{V})_{\ast }({\mathcal{O}}_{{\mathcal{C}}_{V}}(-2\unicode[STIX]{x1D70E}_{V})/{\mathcal{O}}_{{\mathcal{C}}_{V}}(-3\unicode[STIX]{x1D70E}_{V}))\end{eqnarray}$$
vanishes, and let
 $\unicode[STIX]{x1D719}:\widetilde{{\mathcal{C}}}\rightarrow {\mathcal{C}}_{V}$
be the blow-up of
$\unicode[STIX]{x1D719}:\widetilde{{\mathcal{C}}}\rightarrow {\mathcal{C}}_{V}$
be the blow-up of
![]() ${\mathcal{C}}_{V}$
along
${\mathcal{C}}_{V}$
along
![]() $\unicode[STIX]{x1D70E}_{V}(Z)$
. Since
$\unicode[STIX]{x1D70E}_{V}(Z)$
. Since
 $\unicode[STIX]{x1D70E}_{V}(Z)\subset {\mathcal{C}}_{V}$
is a regular subscheme of codimension 2, the exceptional divisor
$\unicode[STIX]{x1D70E}_{V}(Z)\subset {\mathcal{C}}_{V}$
is a regular subscheme of codimension 2, the exceptional divisor
![]() $E$
of the blow-up is a
$E$
of the blow-up is a
![]() $\mathbb{P}^{1}$
-bundle over
$\mathbb{P}^{1}$
-bundle over
![]() $\unicode[STIX]{x1D70E}_{V}(Z)$
. In other words, for all
$\unicode[STIX]{x1D70E}_{V}(Z)$
. In other words, for all
![]() $z\in Z$
, we have
$z\in Z$
, we have
 $$\begin{eqnarray}\widetilde{{\mathcal{C}}}_{z}={\mathcal{C}}_{z}\cup E_{z}={\mathcal{C}}_{z}\cup \mathbb{P}^{1}.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{{\mathcal{C}}}_{z}={\mathcal{C}}_{z}\cup E_{z}={\mathcal{C}}_{z}\cup \mathbb{P}^{1}.\end{eqnarray}$$
Let
![]() $\tilde{\unicode[STIX]{x1D70E}}$
be the strict transform of
$\tilde{\unicode[STIX]{x1D70E}}$
be the strict transform of
![]() $\unicode[STIX]{x1D70E}_{V}$
on
$\unicode[STIX]{x1D70E}_{V}$
on
![]() $\widetilde{{\mathcal{C}}}$
, and observe that
$\widetilde{{\mathcal{C}}}$
, and observe that
![]() $\tilde{\unicode[STIX]{x1D70E}}$
passes through a smooth point of the
$\tilde{\unicode[STIX]{x1D70E}}$
passes through a smooth point of the
![]() $\mathbb{P}^{1}$
component in every fiber over
$\mathbb{P}^{1}$
component in every fiber over
![]() $Z$
. We will construct a map
$Z$
. We will construct a map
![]() $\widetilde{{\mathcal{C}}}\rightarrow {\mathcal{C}}^{\prime }$
which crimps
$\widetilde{{\mathcal{C}}}\rightarrow {\mathcal{C}}^{\prime }$
which crimps
![]() $\tilde{\unicode[STIX]{x1D70E}}$
to a ramphoid cusp, and
$\tilde{\unicode[STIX]{x1D70E}}$
to a ramphoid cusp, and
 ${\mathcal{C}}^{\prime }\rightarrow X$
will be the desired family of ramphoid cuspidal sproutings.
${\mathcal{C}}^{\prime }\rightarrow X$
will be the desired family of ramphoid cuspidal sproutings.
Setting
 $\widetilde{\unicode[STIX]{x1D70B}}:\widetilde{{\mathcal{C}}}\rightarrow {\mathcal{C}}_{V}\rightarrow V$
and
$\widetilde{\unicode[STIX]{x1D70B}}:\widetilde{{\mathcal{C}}}\rightarrow {\mathcal{C}}_{V}\rightarrow V$
and
 $$\begin{eqnarray}\widetilde{{\mathcal{E}}}=\widetilde{\unicode[STIX]{x1D70B}}_{\ast }({\mathcal{O}}_{\widetilde{{\mathcal{C}}}}(-2\tilde{\unicode[STIX]{x1D70E}})/{\mathcal{O}}_{\widetilde{{\mathcal{C}}}}(-4\tilde{\unicode[STIX]{x1D70E}})),\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{{\mathcal{E}}}=\widetilde{\unicode[STIX]{x1D70B}}_{\ast }({\mathcal{O}}_{\widetilde{{\mathcal{C}}}}(-2\tilde{\unicode[STIX]{x1D70E}})/{\mathcal{O}}_{\widetilde{{\mathcal{C}}}}(-4\tilde{\unicode[STIX]{x1D70E}})),\end{eqnarray}$$
we claim that
![]() $e$
induces a section
$e$
induces a section
 $\widetilde{e}:{\mathcal{O}}_{V}\rightarrow \widetilde{{\mathcal{E}}}$
with the property that the composition
$\widetilde{e}:{\mathcal{O}}_{V}\rightarrow \widetilde{{\mathcal{E}}}$
with the property that the composition
 $$\begin{eqnarray}{\mathcal{O}}_{V}\rightarrow \widetilde{{\mathcal{E}}}\rightarrow \widetilde{\unicode[STIX]{x1D70B}}_{\ast }({\mathcal{O}}_{\widetilde{{\mathcal{C}}}}(-2\tilde{\unicode[STIX]{x1D70E}})/{\mathcal{O}}_{\widetilde{{\mathcal{C}}}}(-3\tilde{\unicode[STIX]{x1D70E}}))\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{O}}_{V}\rightarrow \widetilde{{\mathcal{E}}}\rightarrow \widetilde{\unicode[STIX]{x1D70B}}_{\ast }({\mathcal{O}}_{\widetilde{{\mathcal{C}}}}(-2\tilde{\unicode[STIX]{x1D70E}})/{\mathcal{O}}_{\widetilde{{\mathcal{C}}}}(-3\tilde{\unicode[STIX]{x1D70E}}))\end{eqnarray}$$
is never zero. To see this, let
 $U=\operatorname{Spec}R\subset X$
be an open affine subscheme along which
$U=\operatorname{Spec}R\subset X$
be an open affine subscheme along which
![]() ${\mathcal{E}}$
is trivial, and choose local coordinates
${\mathcal{E}}$
is trivial, and choose local coordinates
![]() $a,b$
on
$a,b$
on
 $p^{-1}(U)=\operatorname{Spec}R[a,b]$
such that the tautological section
$p^{-1}(U)=\operatorname{Spec}R[a,b]$
such that the tautological section
![]() $e$
is given by
$e$
is given by
 $at^{2}+bt^{3}$
, where
$at^{2}+bt^{3}$
, where
![]() $t$
is a local equation for
$t$
is a local equation for
![]() $\unicode[STIX]{x1D70E}_{V}$
on
$\unicode[STIX]{x1D70E}_{V}$
on
![]() ${\mathcal{C}}_{V}$
. In these coordinates,
${\mathcal{C}}_{V}$
. In these coordinates,
![]() $\unicode[STIX]{x1D719}$
is the blow-up along
$\unicode[STIX]{x1D719}$
is the blow-up along
 $a=t=0$
. Let
$a=t=0$
. Let
![]() $\tilde{a},\tilde{t}$
be homogeneous coordinates for the blow-up and note that on the chart
$\tilde{a},\tilde{t}$
be homogeneous coordinates for the blow-up and note that on the chart
![]() $\tilde{a}\neq 0$
,
$\tilde{a}\neq 0$
,
 $t^{\prime }:=\tilde{t}/\tilde{a}$
gives a local equation for
$t^{\prime }:=\tilde{t}/\tilde{a}$
gives a local equation for
![]() $\tilde{\unicode[STIX]{x1D70E}}_{V}$
. In these coordinates,
$\tilde{\unicode[STIX]{x1D70E}}_{V}$
. In these coordinates,
![]() $\unicode[STIX]{x1D719}$
is given by
$\unicode[STIX]{x1D719}$
is given by
 $$\begin{eqnarray}(a,b,t)\rightarrow (a,b,at^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}(a,b,t)\rightarrow (a,b,at^{\prime }).\end{eqnarray}$$
The section
 $at^{2}+bt^{3}$
pulls back to
$at^{2}+bt^{3}$
pulls back to
 $a^{3}({t^{\prime }}^{2}+b{t^{\prime }}^{3})$
, and
$a^{3}({t^{\prime }}^{2}+b{t^{\prime }}^{3})$
, and
 ${t^{\prime }}^{2}+b{t^{\prime }}^{3}$
defines a section
${t^{\prime }}^{2}+b{t^{\prime }}^{3}$
defines a section
![]() $\widetilde{e}$
of
$\widetilde{e}$
of
![]() $\widetilde{{\mathcal{E}}}$
over
$\widetilde{{\mathcal{E}}}$
over
![]() $p^{-1}(U)$
with the stated property.
$p^{-1}(U)$
with the stated property.
We will use
![]() $\widetilde{e}$
to construct a map
$\widetilde{e}$
to construct a map
 $\unicode[STIX]{x1D713}:\widetilde{{\mathcal{C}}}\rightarrow {\mathcal{C}}^{\prime }$
such that
$\unicode[STIX]{x1D713}:\widetilde{{\mathcal{C}}}\rightarrow {\mathcal{C}}^{\prime }$
such that
![]() ${\mathcal{C}}^{\prime }$
has a ramphoid cusp along
${\mathcal{C}}^{\prime }$
has a ramphoid cusp along
![]() $\unicode[STIX]{x1D713}\circ \tilde{\unicode[STIX]{x1D70E}}$
. It is sufficient to define
$\unicode[STIX]{x1D713}\circ \tilde{\unicode[STIX]{x1D70E}}$
. It is sufficient to define
![]() $\unicode[STIX]{x1D713}$
locally around
$\unicode[STIX]{x1D713}$
locally around
![]() $\tilde{\unicode[STIX]{x1D70E}}$
, so we may assume that
$\tilde{\unicode[STIX]{x1D70E}}$
, so we may assume that
![]() $\widetilde{\unicode[STIX]{x1D70B}}$
is affine, i.e.
$\widetilde{\unicode[STIX]{x1D70B}}$
is affine, i.e.
 $\widetilde{{\mathcal{C}}}:=\operatorname{Spec}_{V}\widetilde{\unicode[STIX]{x1D70B}}_{\ast }{\mathcal{O}}_{\widetilde{{\mathcal{C}}}}.$
We specify a sheaf of
$\widetilde{{\mathcal{C}}}:=\operatorname{Spec}_{V}\widetilde{\unicode[STIX]{x1D70B}}_{\ast }{\mathcal{O}}_{\widetilde{{\mathcal{C}}}}.$
We specify a sheaf of
![]() ${\mathcal{O}}_{V}$
-subalgebras of
${\mathcal{O}}_{V}$
-subalgebras of
![]() $\widetilde{\unicode[STIX]{x1D70B}}_{\ast }{\mathcal{O}}_{\widetilde{{\mathcal{C}}}}$
as follows: consider the exact sequence
$\widetilde{\unicode[STIX]{x1D70B}}_{\ast }{\mathcal{O}}_{\widetilde{{\mathcal{C}}}}$
as follows: consider the exact sequence
 $$\begin{eqnarray}0\rightarrow \widetilde{\unicode[STIX]{x1D70B}}_{\ast }{\mathcal{O}}_{\widetilde{{\mathcal{C}}}_{V}}(-4\tilde{\unicode[STIX]{x1D70E}})\rightarrow \tilde{\unicode[STIX]{x1D70B}}_{\ast }{\mathcal{O}}_{\widetilde{{\mathcal{C}}}_{V}}(-2\tilde{\unicode[STIX]{x1D70E}})\rightarrow \widetilde{{\mathcal{E}}}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \widetilde{\unicode[STIX]{x1D70B}}_{\ast }{\mathcal{O}}_{\widetilde{{\mathcal{C}}}_{V}}(-4\tilde{\unicode[STIX]{x1D70E}})\rightarrow \tilde{\unicode[STIX]{x1D70B}}_{\ast }{\mathcal{O}}_{\widetilde{{\mathcal{C}}}_{V}}(-2\tilde{\unicode[STIX]{x1D70E}})\rightarrow \widetilde{{\mathcal{E}}}\rightarrow 0\end{eqnarray}$$
and let
 ${\mathcal{F}}\subset \widetilde{\unicode[STIX]{x1D70B}}_{\ast }{\mathcal{O}}_{\widetilde{{\mathcal{C}}}}$
be the sheaf of
${\mathcal{F}}\subset \widetilde{\unicode[STIX]{x1D70B}}_{\ast }{\mathcal{O}}_{\widetilde{{\mathcal{C}}}}$
be the sheaf of
![]() ${\mathcal{O}}_{V}$
-subalgebras generated by any inverse image of
${\mathcal{O}}_{V}$
-subalgebras generated by any inverse image of
![]() $\widetilde{e}$
and all functions in
$\widetilde{e}$
and all functions in
 $\widetilde{\unicode[STIX]{x1D70B}}_{\ast }{\mathcal{O}}_{\widetilde{{\mathcal{C}}}}(-4\tilde{\unicode[STIX]{x1D70E}})$
. We let
$\widetilde{\unicode[STIX]{x1D70B}}_{\ast }{\mathcal{O}}_{\widetilde{{\mathcal{C}}}}(-4\tilde{\unicode[STIX]{x1D70E}})$
. We let
 $\unicode[STIX]{x1D713}:\operatorname{Spec}_{V}\widetilde{\unicode[STIX]{x1D70B}}_{\ast }{\mathcal{O}}_{\widetilde{{\mathcal{C}}}}\rightarrow {\mathcal{C}}^{\prime }:=\operatorname{Spec}_{V}{\mathcal{F}}$
be the map corresponding to the inclusion
$\unicode[STIX]{x1D713}:\operatorname{Spec}_{V}\widetilde{\unicode[STIX]{x1D70B}}_{\ast }{\mathcal{O}}_{\widetilde{{\mathcal{C}}}}\rightarrow {\mathcal{C}}^{\prime }:=\operatorname{Spec}_{V}{\mathcal{F}}$
be the map corresponding to the inclusion
 ${\mathcal{F}}\subset \widetilde{\unicode[STIX]{x1D70B}}_{\ast }{\mathcal{O}}_{\widetilde{{\mathcal{C}}}}$
. By construction, the inclusion of the complete local rings
${\mathcal{F}}\subset \widetilde{\unicode[STIX]{x1D70B}}_{\ast }{\mathcal{O}}_{\widetilde{{\mathcal{C}}}}$
. By construction, the inclusion of the complete local rings
 $\widehat{{\mathcal{O}}}_{C_{v}^{\prime },(\unicode[STIX]{x1D713}\circ \tilde{\unicode[STIX]{x1D70E}})(v)}\subset \widehat{{\mathcal{O}}}_{\widetilde{C}_{v},\tilde{\unicode[STIX]{x1D70E}}(v)}\simeq \mathbb{C}[[t]]$
is of the form
$\widehat{{\mathcal{O}}}_{C_{v}^{\prime },(\unicode[STIX]{x1D713}\circ \tilde{\unicode[STIX]{x1D70E}})(v)}\subset \widehat{{\mathcal{O}}}_{\widetilde{C}_{v},\tilde{\unicode[STIX]{x1D70E}}(v)}\simeq \mathbb{C}[[t]]$
is of the form
 $\mathbb{C}[[t^{2}+bt^{3},t^{5}]]\subset \mathbb{C}[[t]]$
for every
$\mathbb{C}[[t^{2}+bt^{3},t^{5}]]\subset \mathbb{C}[[t]]$
for every
![]() $v\in V$
. Observe that
$v\in V$
. Observe that
 $\mathbb{C}[[t^{2}+bt^{3},t^{5}]]$
is isomorphic to
$\mathbb{C}[[t^{2}+bt^{3},t^{5}]]$
is isomorphic to
 $\mathbb{C}[[x,y]]/(y^{2}-x^{5})$
as a
$\mathbb{C}[[x,y]]/(y^{2}-x^{5})$
as a
![]() $\mathbb{C}$
-algebra.
$\mathbb{C}$
-algebra.
Finally, we claim that
 ${\mathcal{C}}^{\prime }\rightarrow V$
descends to a family of ramphoid cuspidal sproutings over the quotient stack
${\mathcal{C}}^{\prime }\rightarrow V$
descends to a family of ramphoid cuspidal sproutings over the quotient stack
![]() $[V/\mathbb{G}_{m}]$
. It suffices to show that the subsheaf
$[V/\mathbb{G}_{m}]$
. It suffices to show that the subsheaf
 ${\mathcal{F}}\subset \widetilde{\unicode[STIX]{x1D70B}}_{\ast }{\mathcal{O}}_{\widetilde{{\mathcal{C}}}}$
is invariant under the natural action of
${\mathcal{F}}\subset \widetilde{\unicode[STIX]{x1D70B}}_{\ast }{\mathcal{O}}_{\widetilde{{\mathcal{C}}}}$
is invariant under the natural action of
![]() $\mathbb{G}_{m}$
on
$\mathbb{G}_{m}$
on
![]() $V$
. Using the same local coordinates introduced above, the sheaf
$V$
. Using the same local coordinates introduced above, the sheaf
![]() ${\mathcal{F}}$
is given over the open set
${\mathcal{F}}$
is given over the open set
 $\operatorname{Spec}R[a,b]$
by the
$\operatorname{Spec}R[a,b]$
by the
![]() $R[a,b]$
-algebra generated by
$R[a,b]$
-algebra generated by
 ${t^{\prime }}^{2}+b{t^{\prime }}^{3}$
and
${t^{\prime }}^{2}+b{t^{\prime }}^{3}$
and
![]() ${t^{\prime }}^{5}$
, where
${t^{\prime }}^{5}$
, where
![]() $t^{\prime }$
is a local equation for
$t^{\prime }$
is a local equation for
![]() $\tilde{\unicode[STIX]{x1D70E}}$
on
$\tilde{\unicode[STIX]{x1D70E}}$
on
![]() $\widetilde{{\mathcal{C}}}$
. To see that this algebra is
$\widetilde{{\mathcal{C}}}$
. To see that this algebra is
![]() $\mathbb{G}_{m}$
-invariant, note that the
$\mathbb{G}_{m}$
-invariant, note that the
![]() $\mathbb{G}_{m}$
-action on
$\mathbb{G}_{m}$
-action on
 $V=\operatorname{Spec}R[a,b]$
(acting with weight 1 on
$V=\operatorname{Spec}R[a,b]$
(acting with weight 1 on
![]() $a$
and
$a$
and
![]() $b$
) extends canonically to a
$b$
) extends canonically to a
![]() $\mathbb{G}_{m}$
-action on the blow-up, where
$\mathbb{G}_{m}$
-action on the blow-up, where
![]() $\mathbb{G}_{m}$
acts on
$\mathbb{G}_{m}$
acts on
![]() $\tilde{a}$
and
$\tilde{a}$
and
![]() $\tilde{t}$
with weights
$\tilde{t}$
with weights
![]() $1$
and
$1$
and
![]() $0$
, respectively. Thus,
$0$
, respectively. Thus,
![]() $\mathbb{G}_{m}$
acts on
$\mathbb{G}_{m}$
acts on
 $t^{\prime }=\tilde{t}/\tilde{a}$
with weight
$t^{\prime }=\tilde{t}/\tilde{a}$
with weight
![]() $-1$
, so that
$-1$
, so that
 ${t^{\prime }}^{2}+b{t^{\prime }}^{3}$
is a semi-invariant. It follows that the algebra generated by
${t^{\prime }}^{2}+b{t^{\prime }}^{3}$
is a semi-invariant. It follows that the algebra generated by
 ${t^{\prime }}^{2}+b{t^{\prime }}^{3}$
and
${t^{\prime }}^{2}+b{t^{\prime }}^{3}$
and
![]() ${t^{\prime }}^{5}$
is
${t^{\prime }}^{5}$
is
![]() $\mathbb{G}_{m}$
-invariant, as desired. Thus, we obtain a family
$\mathbb{G}_{m}$
-invariant, as desired. Thus, we obtain a family
 $({\mathcal{C}}^{\prime }\rightarrow [V/\mathbb{G}_{m}],\unicode[STIX]{x1D713}\circ \tilde{\unicode[STIX]{x1D70E}})$
in
$({\mathcal{C}}^{\prime }\rightarrow [V/\mathbb{G}_{m}],\unicode[STIX]{x1D713}\circ \tilde{\unicode[STIX]{x1D70E}})$
in
 $\operatorname{Sprout}_{g,n}(A_{4})$
, as desired.
$\operatorname{Sprout}_{g,n}(A_{4})$
, as desired.
To define an inverse map
 $\unicode[STIX]{x1D6FE}^{-1}:\operatorname{Sprout}_{g,n}(A_{4})\rightarrow [V/\mathbb{G}_{m}]$
, we start with a family
$\unicode[STIX]{x1D6FE}^{-1}:\operatorname{Sprout}_{g,n}(A_{4})\rightarrow [V/\mathbb{G}_{m}]$
, we start with a family
 $({\mathcal{C}}\rightarrow X,\unicode[STIX]{x1D70E})$
in
$({\mathcal{C}}\rightarrow X,\unicode[STIX]{x1D70E})$
in
 ${\mathcal{U}}_{g,n}(A_{4})$
such that
${\mathcal{U}}_{g,n}(A_{4})$
such that
![]() ${\mathcal{C}}$
has an
${\mathcal{C}}$
has an
![]() $A_{4}$
-singularity along
$A_{4}$
-singularity along
![]() $\unicode[STIX]{x1D70E}$
. We must construct a map
$\unicode[STIX]{x1D70E}$
. We must construct a map
 $X\rightarrow [V({\mathcal{E}})/\mathbb{G}_{m}]$
. By taking the stable pointed normalization of
$X\rightarrow [V({\mathcal{E}})/\mathbb{G}_{m}]$
. By taking the stable pointed normalization of
![]() ${\mathcal{C}}$
along
${\mathcal{C}}$
along
![]() $\unicode[STIX]{x1D70E}$
, we obtain a diagram
$\unicode[STIX]{x1D70E}$
, we obtain a diagram

satisfying:
-
(i)
 $(\widetilde{{\mathcal{C}}}\rightarrow X,\tilde{\unicode[STIX]{x1D70E}})$
is a family of
$(\widetilde{{\mathcal{C}}}\rightarrow X,\tilde{\unicode[STIX]{x1D70E}})$
is a family of
 $(n+1)$
-pointed curves;
$(n+1)$
-pointed curves; -
(ii)
 $\unicode[STIX]{x1D713}$
is the pointed normalization of
$\unicode[STIX]{x1D713}$
is the pointed normalization of
 ${\mathcal{C}}$
along
${\mathcal{C}}$
along
 $\unicode[STIX]{x1D70E}$
, i.e.
$\unicode[STIX]{x1D70E}$
, i.e.
 $\unicode[STIX]{x1D713}$
is finite and restricts to an isomorphism on the open set
$\unicode[STIX]{x1D713}$
is finite and restricts to an isomorphism on the open set
 $\widetilde{{\mathcal{C}}}-\tilde{\unicode[STIX]{x1D70E}}$
; and
$\widetilde{{\mathcal{C}}}-\tilde{\unicode[STIX]{x1D70E}}$
; and -
(iii)
 $\unicode[STIX]{x1D719}$
is the stabilization of
$\unicode[STIX]{x1D719}$
is the stabilization of
 $(\widetilde{{\mathcal{C}}},\tilde{\unicode[STIX]{x1D70E}})$
, i.e.
$(\widetilde{{\mathcal{C}}},\tilde{\unicode[STIX]{x1D70E}})$
, i.e.
 $\unicode[STIX]{x1D719}$
is the morphism associated to a high multiple of the relatively nef line bundle
$\unicode[STIX]{x1D719}$
is the morphism associated to a high multiple of the relatively nef line bundle
 $\unicode[STIX]{x1D714}_{\widetilde{{\mathcal{C}}}/X}(\tilde{\unicode[STIX]{x1D70E}})$
.
$\unicode[STIX]{x1D714}_{\widetilde{{\mathcal{C}}}/X}(\tilde{\unicode[STIX]{x1D70E}})$
.
The family
 $({\mathcal{C}}^{s}\rightarrow X,\unicode[STIX]{x1D70E}_{i}^{s})$
induces a map
$({\mathcal{C}}^{s}\rightarrow X,\unicode[STIX]{x1D70E}_{i}^{s})$
induces a map
 $X\rightarrow {\mathcal{U}}_{g-2,n+1}(A_{4})$
, and we must show that this lifts to define a map
$X\rightarrow {\mathcal{U}}_{g-2,n+1}(A_{4})$
, and we must show that this lifts to define a map
 $X\rightarrow [V({\mathcal{E}})/\mathbb{G}_{m}]$
. To see this, let
$X\rightarrow [V({\mathcal{E}})/\mathbb{G}_{m}]$
. To see this, let
![]() ${\mathcal{F}}$
be the coherent sheaf defined by the following exact sequence:
${\mathcal{F}}$
be the coherent sheaf defined by the following exact sequence:
 $$\begin{eqnarray}0\rightarrow \unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{{\mathcal{C}}}\cap \widetilde{\unicode[STIX]{x1D70B}}_{\ast }{\mathcal{O}}_{\widetilde{{\mathcal{C}}}}(-4\tilde{\unicode[STIX]{x1D70E}})\subset \unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{{\mathcal{C}}}\cap \widetilde{\unicode[STIX]{x1D70B}}_{\ast }{\mathcal{O}}_{\widetilde{{\mathcal{C}}}}(-2\tilde{\unicode[STIX]{x1D70E}})\rightarrow {\mathcal{F}}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{{\mathcal{C}}}\cap \widetilde{\unicode[STIX]{x1D70B}}_{\ast }{\mathcal{O}}_{\widetilde{{\mathcal{C}}}}(-4\tilde{\unicode[STIX]{x1D70E}})\subset \unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{{\mathcal{C}}}\cap \widetilde{\unicode[STIX]{x1D70B}}_{\ast }{\mathcal{O}}_{\widetilde{{\mathcal{C}}}}(-2\tilde{\unicode[STIX]{x1D70E}})\rightarrow {\mathcal{F}}\rightarrow 0.\end{eqnarray}$$
The condition that
![]() ${\mathcal{C}}$
has a ramphoid cusp along
${\mathcal{C}}$
has a ramphoid cusp along
![]() $\unicode[STIX]{x1D713}\circ \tilde{\unicode[STIX]{x1D70E}}$
implies that
$\unicode[STIX]{x1D713}\circ \tilde{\unicode[STIX]{x1D70E}}$
implies that
 ${\mathcal{F}}\subset \widetilde{\unicode[STIX]{x1D70B}}_{\ast }{\mathcal{O}}_{\widetilde{{\mathcal{C}}}}(-2\unicode[STIX]{x1D70E})/{\mathcal{O}}_{\widetilde{{\mathcal{C}}}}(-4\unicode[STIX]{x1D70E})$
is a rank-one sub-bundle. In particular,
${\mathcal{F}}\subset \widetilde{\unicode[STIX]{x1D70B}}_{\ast }{\mathcal{O}}_{\widetilde{{\mathcal{C}}}}(-2\unicode[STIX]{x1D70E})/{\mathcal{O}}_{\widetilde{{\mathcal{C}}}}(-4\unicode[STIX]{x1D70E})$
is a rank-one sub-bundle. In particular,
![]() ${\mathcal{F}}$
induces a sub-bundle of
${\mathcal{F}}$
induces a sub-bundle of
 $\unicode[STIX]{x1D70B}_{\ast }^{s}{\mathcal{O}}_{{\mathcal{C}}^{s}}(-2\unicode[STIX]{x1D70E}^{s})/{\mathcal{O}}_{{\mathcal{C}}^{s}}(-4\unicode[STIX]{x1D70E}^{s})$
over the locus of fibers on which
$\unicode[STIX]{x1D70B}_{\ast }^{s}{\mathcal{O}}_{{\mathcal{C}}^{s}}(-2\unicode[STIX]{x1D70E}^{s})/{\mathcal{O}}_{{\mathcal{C}}^{s}}(-4\unicode[STIX]{x1D70E}^{s})$
over the locus of fibers on which
![]() $\unicode[STIX]{x1D719}$
is an isomorphism. A local computation, similar to the one performed in the definition of
$\unicode[STIX]{x1D719}$
is an isomorphism. A local computation, similar to the one performed in the definition of
![]() $\unicode[STIX]{x1D6FE}$
, shows that
$\unicode[STIX]{x1D6FE}$
, shows that
![]() ${\mathcal{F}}$
extends to a subsheaf of
${\mathcal{F}}$
extends to a subsheaf of
 $\unicode[STIX]{x1D70B}_{\ast }^{s}{\mathcal{O}}_{{\mathcal{C}}^{s}}(-2\unicode[STIX]{x1D70E}^{s})/{\mathcal{O}}_{{\mathcal{C}}^{s}}(-4\unicode[STIX]{x1D70E}^{s})$
over all of
$\unicode[STIX]{x1D70B}_{\ast }^{s}{\mathcal{O}}_{{\mathcal{C}}^{s}}(-2\unicode[STIX]{x1D70E}^{s})/{\mathcal{O}}_{{\mathcal{C}}^{s}}(-4\unicode[STIX]{x1D70E}^{s})$
over all of
![]() $X$
(though not a sub-bundle; the morphism on fibers is zero precisely where
$X$
(though not a sub-bundle; the morphism on fibers is zero precisely where
![]() $\unicode[STIX]{x1D719}$
fails to be an isomorphism). The subsheaf
$\unicode[STIX]{x1D719}$
fails to be an isomorphism). The subsheaf
![]() ${\mathcal{F}}\subset {\mathcal{E}}$
induces the desired morphism
${\mathcal{F}}\subset {\mathcal{E}}$
induces the desired morphism
 $X\rightarrow [V({\mathcal{E}})/\mathbb{G}_{m}]$
.◻
$X\rightarrow [V({\mathcal{E}})/\mathbb{G}_{m}]$
.◻
Proposition 4.10. Let
 $\unicode[STIX]{x1D6FC}_{c}\in \{9/11,7/10,2/3\}$
and suppose that
$\unicode[STIX]{x1D6FC}_{c}\in \{9/11,7/10,2/3\}$
and suppose that
 $\overline{{\mathcal{M}}}_{g^{\prime },n^{\prime }}(\unicode[STIX]{x1D6FC}_{c})$
admits a proper good moduli space for all
$\overline{{\mathcal{M}}}_{g^{\prime },n^{\prime }}(\unicode[STIX]{x1D6FC}_{c})$
admits a proper good moduli space for all
![]() $(g^{\prime },n^{\prime })$
with
$(g^{\prime },n^{\prime })$
with
![]() $g^{\prime }<g$
. Then
$g^{\prime }<g$
. Then
 $\overline{{\mathcal{S}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
admits a proper good moduli space.
$\overline{{\mathcal{S}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
admits a proper good moduli space.
Proof. Let
 $\unicode[STIX]{x1D6FC}_{c}=9/11$
. By Lemma 4.3, we may assume that
$\unicode[STIX]{x1D6FC}_{c}=9/11$
. By Lemma 4.3, we may assume that
 $(g,n)\neq (1,1)$
. By Proposition 4.9(i), there is a locally free sheaf
$(g,n)\neq (1,1)$
. By Proposition 4.9(i), there is a locally free sheaf
![]() ${\mathcal{E}}$
on
${\mathcal{E}}$
on
 $\overline{{\mathcal{M}}}_{g-1,n+1}(9/11)$
such that
$\overline{{\mathcal{M}}}_{g-1,n+1}(9/11)$
such that
 $[V({\mathcal{E}})/\mathbb{G}_{m}]$
is the base of the universal family of cuspidal sproutings of curves in
$[V({\mathcal{E}})/\mathbb{G}_{m}]$
is the base of the universal family of cuspidal sproutings of curves in
 $\overline{{\mathcal{M}}}_{g-1,n+1}(9/11)$
. By Lemma 4.2, the fibers of this family are
$\overline{{\mathcal{M}}}_{g-1,n+1}(9/11)$
. By Lemma 4.2, the fibers of this family are
![]() $9/11$
-stable, so there is an induced map
$9/11$
-stable, so there is an induced map
 $$\begin{eqnarray}\unicode[STIX]{x1D6F9}:[V({\mathcal{E}})/\mathbb{G}_{m}]\rightarrow \overline{{\mathcal{M}}}_{g,n}(9/11).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}:[V({\mathcal{E}})/\mathbb{G}_{m}]\rightarrow \overline{{\mathcal{M}}}_{g,n}(9/11).\end{eqnarray}$$
By Lemma 4.5,
![]() $\unicode[STIX]{x1D6F9}$
maps surjectively onto
$\unicode[STIX]{x1D6F9}$
maps surjectively onto
 $\overline{{\mathcal{S}}}_{g,n}(9/11)$
. Furthermore,
$\overline{{\mathcal{S}}}_{g,n}(9/11)$
. Furthermore,
![]() $\unicode[STIX]{x1D6F9}$
is finite by Proposition 4.7. By hypothesis,
$\unicode[STIX]{x1D6F9}$
is finite by Proposition 4.7. By hypothesis,
 $\overline{{\mathcal{M}}}_{g-1,n+1}(9/11)$
and therefore
$\overline{{\mathcal{M}}}_{g-1,n+1}(9/11)$
and therefore
 $[V({\mathcal{E}})/\mathbb{G}_{m}]$
admits a proper good moduli space. Thus,
$[V({\mathcal{E}})/\mathbb{G}_{m}]$
admits a proper good moduli space. Thus,
 $\overline{{\mathcal{S}}}_{g,n}(9/11)$
admits a proper good moduli space by Proposition 1.4.
$\overline{{\mathcal{S}}}_{g,n}(9/11)$
admits a proper good moduli space by Proposition 1.4.
Let
 $\unicode[STIX]{x1D6FC}_{c}=7/10$
. By Lemma 4.3, we may assume that
$\unicode[STIX]{x1D6FC}_{c}=7/10$
. By Lemma 4.3, we may assume that
 $(g,n)\neq (1,2)$
. If
$(g,n)\neq (1,2)$
. If
![]() $g\geqslant 2$
, Proposition 4.9(ii) provides a locally free sheaf
$g\geqslant 2$
, Proposition 4.9(ii) provides a locally free sheaf
![]() ${\mathcal{E}}$
on
${\mathcal{E}}$
on
 $\overline{{\mathcal{M}}}_{g-2,n+2}(7/10)$
such that
$\overline{{\mathcal{M}}}_{g-2,n+2}(7/10)$
such that
 $[V({\mathcal{E}})/\mathbb{G}_{m}]$
is the base of the universal family of tacnodal sproutings of curves in
$[V({\mathcal{E}})/\mathbb{G}_{m}]$
is the base of the universal family of tacnodal sproutings of curves in
 $\overline{{\mathcal{M}}}_{g-2,n+2}(7/10)$
, and there is an induced map
$\overline{{\mathcal{M}}}_{g-2,n+2}(7/10)$
, and there is an induced map
 $[V({\mathcal{E}})/\mathbb{G}_{m}]\rightarrow \overline{{\mathcal{M}}}_{g,n}(7/10).$
Similarly, for every pair of integers
$[V({\mathcal{E}})/\mathbb{G}_{m}]\rightarrow \overline{{\mathcal{M}}}_{g,n}(7/10).$
Similarly, for every pair of integers
![]() $(i,m)$
such that
$(i,m)$
such that
 $\overline{{\mathcal{M}}}_{g-i-1,n-m+1}(7/10)\times \overline{{\mathcal{M}}}_{i,m+1}(7/10)$
is defined, by Proposition 4.9(iii), there is a locally free sheaf
$\overline{{\mathcal{M}}}_{g-i-1,n-m+1}(7/10)\times \overline{{\mathcal{M}}}_{i,m+1}(7/10)$
is defined, by Proposition 4.9(iii), there is a locally free sheaf
![]() ${\mathcal{E}}$
on
${\mathcal{E}}$
on
 $\overline{{\mathcal{M}}}_{g-i-1,n-m+1}(7/10)\times \overline{{\mathcal{M}}}_{i,m+1}(7/10)$
such that
$\overline{{\mathcal{M}}}_{g-i-1,n-m+1}(7/10)\times \overline{{\mathcal{M}}}_{i,m+1}(7/10)$
such that
 $[V({\mathcal{E}})/\mathbb{G}_{m}]$
is the universal family of tacnodal sproutings. By Lemma 4.2, there are induced maps
$[V({\mathcal{E}})/\mathbb{G}_{m}]$
is the universal family of tacnodal sproutings. By Lemma 4.2, there are induced maps
 $[V({\mathcal{E}})/\mathbb{G}_{m}]\rightarrow \overline{{\mathcal{M}}}_{g,n}(7/10).$
Finally, Proposition 4.9(iv) provides a locally free sheaf on
$[V({\mathcal{E}})/\mathbb{G}_{m}]\rightarrow \overline{{\mathcal{M}}}_{g,n}(7/10).$
Finally, Proposition 4.9(iv) provides a locally free sheaf on
 $\overline{{\mathcal{M}}}_{g-1,n}(7/10)$
such that
$\overline{{\mathcal{M}}}_{g-1,n}(7/10)$
such that
 $[V({\mathcal{E}})/\mathbb{G}_{m}]$
is the base of the universal family of one-sided tacnodal sproutings of curves in
$[V({\mathcal{E}})/\mathbb{G}_{m}]$
is the base of the universal family of one-sided tacnodal sproutings of curves in
 $\overline{{\mathcal{M}}}_{g-1,n}(7/10)$
. By Lemma 4.2, there is an induced map
$\overline{{\mathcal{M}}}_{g-1,n}(7/10)$
. By Lemma 4.2, there is an induced map
 $[V({\mathcal{E}})/\mathbb{G}_{m}]\rightarrow \overline{{\mathcal{M}}}_{g,n}(7/10).$
The union of the maps
$[V({\mathcal{E}})/\mathbb{G}_{m}]\rightarrow \overline{{\mathcal{M}}}_{g,n}(7/10).$
The union of the maps
 $[V({\mathcal{E}})/\mathbb{G}_{m}]\rightarrow \overline{{\mathcal{M}}}_{g,n}(7/10)$
covers
$[V({\mathcal{E}})/\mathbb{G}_{m}]\rightarrow \overline{{\mathcal{M}}}_{g,n}(7/10)$
covers
 $\overline{{\mathcal{S}}}_{g,n}(7/10)$
by Lemma 4.5. Furthermore, each map is finite by Proposition 4.7. By hypothesis, each of the stacky projective bundles
$\overline{{\mathcal{S}}}_{g,n}(7/10)$
by Lemma 4.5. Furthermore, each map is finite by Proposition 4.7. By hypothesis, each of the stacky projective bundles
 $[V({\mathcal{E}})/\mathbb{G}_{m}]$
admits a proper good moduli space, and therefore so does
$[V({\mathcal{E}})/\mathbb{G}_{m}]$
admits a proper good moduli space, and therefore so does
 $\overline{{\mathcal{S}}}_{g,n}(7/10)$
by Proposition 1.4.
$\overline{{\mathcal{S}}}_{g,n}(7/10)$
by Proposition 1.4.
Let
 $\unicode[STIX]{x1D6FC}_{c}=2/3$
. By Lemma 4.3, we may assume that
$\unicode[STIX]{x1D6FC}_{c}=2/3$
. By Lemma 4.3, we may assume that
 $(g,n)\neq (2,1)$
. By Proposition 4.9(v), there is a locally free sheaf
$(g,n)\neq (2,1)$
. By Proposition 4.9(v), there is a locally free sheaf
![]() ${\mathcal{E}}$
on
${\mathcal{E}}$
on
 $\overline{{\mathcal{M}}}_{g-2,n+1}(2/3)$
such that
$\overline{{\mathcal{M}}}_{g-2,n+1}(2/3)$
such that
 $[V({\mathcal{E}})/\mathbb{G}_{m}]$
is the base of the universal family of ramphoid cuspidal sproutings of curves in
$[V({\mathcal{E}})/\mathbb{G}_{m}]$
is the base of the universal family of ramphoid cuspidal sproutings of curves in
 $\overline{{\mathcal{M}}}_{g-2,n+1}(2/3)$
. By Lemma 4.2, there is an induced map
$\overline{{\mathcal{M}}}_{g-2,n+1}(2/3)$
. By Lemma 4.2, there is an induced map
 $\unicode[STIX]{x1D6F9}:[V({\mathcal{E}})/\mathbb{G}_{m}]\rightarrow \overline{{\mathcal{M}}}_{g,n}(2/3)$
which maps surjectively onto
$\unicode[STIX]{x1D6F9}:[V({\mathcal{E}})/\mathbb{G}_{m}]\rightarrow \overline{{\mathcal{M}}}_{g,n}(2/3)$
which maps surjectively onto
 $\overline{{\mathcal{S}}}_{g,n}(2/3)$
by Lemma 4.5. Furthermore,
$\overline{{\mathcal{S}}}_{g,n}(2/3)$
by Lemma 4.5. Furthermore,
![]() $\unicode[STIX]{x1D6F9}$
is finite by Proposition 4.7. Thus,
$\unicode[STIX]{x1D6F9}$
is finite by Proposition 4.7. Thus,
 $\overline{{\mathcal{S}}}_{g,n}(2/3)$
admits a proper good moduli space by Proposition 1.4.◻
$\overline{{\mathcal{S}}}_{g,n}(2/3)$
admits a proper good moduli space by Proposition 1.4.◻
4.3 Existence for
 $\overline{{\mathcal{H}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
$\overline{{\mathcal{H}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
In this section, we use induction on
![]() $g$
to prove that
$g$
to prove that
 $\overline{{\mathcal{H}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
admits a good moduli space. The base case is handled by the following easy lemma.
$\overline{{\mathcal{H}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
admits a good moduli space. The base case is handled by the following easy lemma.
Lemma 4.11. We have
 $$\begin{eqnarray}\displaystyle \overline{{\mathcal{H}}}_{1,1}(9/11) & = & \displaystyle [\mathbb{A}^{2}/\mathbb{G}_{m}],\quad \text{with weights }4,6;\nonumber\\ \displaystyle \overline{{\mathcal{H}}}_{1,2}(7/10) & = & \displaystyle [\mathbb{A}^{3}/\mathbb{G}_{m}],\quad \text{with weights }2,3,4;\text{ and}\nonumber\\ \displaystyle \overline{{\mathcal{H}}}_{2,1}(2/3) & = & \displaystyle [\mathbb{A}^{4}/\mathbb{G}_{m}],\quad \text{with weights }4,6,8,10.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \overline{{\mathcal{H}}}_{1,1}(9/11) & = & \displaystyle [\mathbb{A}^{2}/\mathbb{G}_{m}],\quad \text{with weights }4,6;\nonumber\\ \displaystyle \overline{{\mathcal{H}}}_{1,2}(7/10) & = & \displaystyle [\mathbb{A}^{3}/\mathbb{G}_{m}],\quad \text{with weights }2,3,4;\text{ and}\nonumber\\ \displaystyle \overline{{\mathcal{H}}}_{2,1}(2/3) & = & \displaystyle [\mathbb{A}^{4}/\mathbb{G}_{m}],\quad \text{with weights }4,6,8,10.\nonumber\end{eqnarray}$$
In particular,
 $\overline{{\mathcal{H}}}_{1,1}(9/11)$
,
$\overline{{\mathcal{H}}}_{1,1}(9/11)$
,
 $\overline{{\mathcal{H}}}_{1,2}(7/10)$
, and
$\overline{{\mathcal{H}}}_{1,2}(7/10)$
, and
 $\overline{{\mathcal{H}}}_{2,1}(2/3)$
each admit a good moduli space.
$\overline{{\mathcal{H}}}_{2,1}(2/3)$
each admit a good moduli space.
Proof. We describe the case of
 $\overline{{\mathcal{H}}}_{2,1}(2/3)$
, as the other two are essentially identical. Consider the family of Weierstrass tails over
$\overline{{\mathcal{H}}}_{2,1}(2/3)$
, as the other two are essentially identical. Consider the family of Weierstrass tails over
![]() $\mathbb{A}^{4}$
given by
$\mathbb{A}^{4}$
given by
 $$\begin{eqnarray}y^{2}=x^{5}z+a_{3}x^{3}z^{3}+a_{2}x^{2}z^{4}+a_{1}xz^{5}+a_{0}z^{6},\end{eqnarray}$$
$$\begin{eqnarray}y^{2}=x^{5}z+a_{3}x^{3}z^{3}+a_{2}x^{2}z^{4}+a_{1}xz^{5}+a_{0}z^{6},\end{eqnarray}$$
where the Weierstrass section is given by
![]() $[1,0,0]$
. Since
$[1,0,0]$
. Since
![]() $\mathbb{G}_{m}$
acts on the base and total space of this family by
$\mathbb{G}_{m}$
acts on the base and total space of this family by
 $$\begin{eqnarray}x\rightarrow \unicode[STIX]{x1D706}^{2}x,\quad y\rightarrow \unicode[STIX]{x1D706}^{5}y,\quad a_{i}\rightarrow \unicode[STIX]{x1D706}^{10-2i}a_{i},\end{eqnarray}$$
$$\begin{eqnarray}x\rightarrow \unicode[STIX]{x1D706}^{2}x,\quad y\rightarrow \unicode[STIX]{x1D706}^{5}y,\quad a_{i}\rightarrow \unicode[STIX]{x1D706}^{10-2i}a_{i},\end{eqnarray}$$
the family descends to
 $[\mathbb{A}^{4}/\mathbb{G}_{m}]$
. One checks that the induced map
$[\mathbb{A}^{4}/\mathbb{G}_{m}]$
. One checks that the induced map
 $[\mathbb{A}^{4}/\mathbb{G}_{m}]\rightarrow \overline{{\mathcal{H}}}_{2,1}(2/3)$
is an isomorphism.◻
$[\mathbb{A}^{4}/\mathbb{G}_{m}]\rightarrow \overline{{\mathcal{H}}}_{2,1}(2/3)$
is an isomorphism.◻
Lemma 4.11 gives an explicit description of the stack of elliptic tails, elliptic bridges, and Weierstrass tails. In the case
 $\unicode[STIX]{x1D6FC}_{c}=7/10$
(respectively,
$\unicode[STIX]{x1D6FC}_{c}=7/10$
(respectively,
 $\unicode[STIX]{x1D6FC}_{c}=2/3$
), we will also need an explicit description of the stack of elliptic chains (respectively, Weierstrass chains) of length
$\unicode[STIX]{x1D6FC}_{c}=2/3$
), we will also need an explicit description of the stack of elliptic chains (respectively, Weierstrass chains) of length
![]() $r$
.
$r$
.
Lemma 4.12. Let
![]() $r\geqslant 1$
be an integer and let
$r\geqslant 1$
be an integer and let
 $$\begin{eqnarray}{\mathcal{E}}{\mathcal{C}}_{r}\subset \overline{{\mathcal{M}}}_{2r-1,2}(7/10)\quad (\text{respectively, }{\mathcal{W}}{\mathcal{C}}_{r}\subset \overline{{\mathcal{M}}}_{2r,1}(2/3))\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{E}}{\mathcal{C}}_{r}\subset \overline{{\mathcal{M}}}_{2r-1,2}(7/10)\quad (\text{respectively, }{\mathcal{W}}{\mathcal{C}}_{r}\subset \overline{{\mathcal{M}}}_{2r,1}(2/3))\end{eqnarray}$$
denote the closure of the locally closed substack of elliptic chains (respectively, Weierstrass chains) of length
![]() $r$
. Then
$r$
. Then
![]() ${\mathcal{E}}{\mathcal{C}}_{r}$
(respectively,
${\mathcal{E}}{\mathcal{C}}_{r}$
(respectively,
![]() ${\mathcal{W}}{\mathcal{C}}_{r}$
) admits a good moduli space.
${\mathcal{W}}{\mathcal{C}}_{r}$
) admits a good moduli space.
Proof. For elliptic chains, Lemma 4.11 handles the case
![]() $r=1$
as
$r=1$
as
 ${\mathcal{E}}{\mathcal{C}}_{1}=\overline{{\mathcal{H}}}_{1,2}(7/10)$
. By induction on
${\mathcal{E}}{\mathcal{C}}_{1}=\overline{{\mathcal{H}}}_{1,2}(7/10)$
. By induction on
![]() $r$
, we may assume that
$r$
, we may assume that
![]() ${\mathcal{E}}{\mathcal{C}}_{r-1}$
admits a good moduli space. By Proposition 4.9(iii), there is a locally free sheaf
${\mathcal{E}}{\mathcal{C}}_{r-1}$
admits a good moduli space. By Proposition 4.9(iii), there is a locally free sheaf
![]() ${\mathcal{E}}$
on
${\mathcal{E}}$
on
 ${\mathcal{E}}{\mathcal{C}}_{r-1}\times \overline{{\mathcal{H}}}_{1,2}(7/10)$
such that
${\mathcal{E}}{\mathcal{C}}_{r-1}\times \overline{{\mathcal{H}}}_{1,2}(7/10)$
such that
 $[V({\mathcal{E}})/\mathbb{G}_{m}]$
is the base of the universal family of tacnodal sproutings over
$[V({\mathcal{E}})/\mathbb{G}_{m}]$
is the base of the universal family of tacnodal sproutings over
 ${\mathcal{E}}{\mathcal{C}}_{r-1}\times \overline{{\mathcal{H}}}_{1,2}(7/10)$
. By Lemma 4.2, there is an induced morphism
${\mathcal{E}}{\mathcal{C}}_{r-1}\times \overline{{\mathcal{H}}}_{1,2}(7/10)$
. By Lemma 4.2, there is an induced morphism
 $\unicode[STIX]{x1D6F9}:[{\mathcal{V}}({\mathcal{E}})/\mathbb{G}_{m}]\rightarrow \overline{{\mathcal{M}}}_{2r-1,2}(7/10).$
The image of
$\unicode[STIX]{x1D6F9}:[{\mathcal{V}}({\mathcal{E}})/\mathbb{G}_{m}]\rightarrow \overline{{\mathcal{M}}}_{2r-1,2}(7/10).$
The image of
![]() $\unicode[STIX]{x1D6F9}$
is
$\unicode[STIX]{x1D6F9}$
is
![]() ${\mathcal{E}}{\mathcal{C}}_{r}$
, and
${\mathcal{E}}{\mathcal{C}}_{r}$
, and
![]() $\unicode[STIX]{x1D6F9}$
is finite by Proposition 4.7. Since
$\unicode[STIX]{x1D6F9}$
is finite by Proposition 4.7. Since
 ${\mathcal{E}}{\mathcal{C}}_{r-1}\times \overline{{\mathcal{H}}}_{1,2}(7/10)$
admits a good moduli space, Proposition 1.4 implies that
${\mathcal{E}}{\mathcal{C}}_{r-1}\times \overline{{\mathcal{H}}}_{1,2}(7/10)$
admits a good moduli space, Proposition 1.4 implies that
![]() ${\mathcal{E}}{\mathcal{C}}_{r}$
admits a good moduli space.
${\mathcal{E}}{\mathcal{C}}_{r}$
admits a good moduli space.
For Weierstrass chains, Lemma 4.11 again handles the case
![]() $r=1$
as
$r=1$
as
 ${\mathcal{W}}{\mathcal{C}}_{1}=\overline{{\mathcal{H}}}_{2,1}(2/3)$
. By induction, we may assume that
${\mathcal{W}}{\mathcal{C}}_{1}=\overline{{\mathcal{H}}}_{2,1}(2/3)$
. By induction, we may assume that
![]() ${\mathcal{W}}{\mathcal{C}}_{r-1}$
admits a good moduli space. By Proposition 4.9(iii), there is a locally free sheaf
${\mathcal{W}}{\mathcal{C}}_{r-1}$
admits a good moduli space. By Proposition 4.9(iii), there is a locally free sheaf
![]() ${\mathcal{E}}$
on
${\mathcal{E}}$
on
 $\overline{{\mathcal{H}}}_{1,2}(7/10)\times {\mathcal{W}}{\mathcal{C}}_{r-1}$
such that
$\overline{{\mathcal{H}}}_{1,2}(7/10)\times {\mathcal{W}}{\mathcal{C}}_{r-1}$
such that
 $[V({\mathcal{E}})/\mathbb{G}_{m}]$
is the base of the universal family of tacnodal sproutings over
$[V({\mathcal{E}})/\mathbb{G}_{m}]$
is the base of the universal family of tacnodal sproutings over
 $\overline{{\mathcal{H}}}_{1,2}(7/10)\times {\mathcal{W}}{\mathcal{C}}_{r-1}$
. Indeed, we may take
$\overline{{\mathcal{H}}}_{1,2}(7/10)\times {\mathcal{W}}{\mathcal{C}}_{r-1}$
. Indeed, we may take
![]() ${\mathcal{E}}$
to be
${\mathcal{E}}$
to be
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{\ast }({\mathcal{O}}_{{\mathcal{C}}}(-\unicode[STIX]{x1D70E})/{\mathcal{O}}_{{\mathcal{C}}}(-2\unicode[STIX]{x1D70E})\oplus {\mathcal{O}}_{{\mathcal{C}}}(-\unicode[STIX]{x1D70F})/{\mathcal{O}}_{{\mathcal{C}}}(-2\unicode[STIX]{x1D70F})),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{\ast }({\mathcal{O}}_{{\mathcal{C}}}(-\unicode[STIX]{x1D70E})/{\mathcal{O}}_{{\mathcal{C}}}(-2\unicode[STIX]{x1D70E})\oplus {\mathcal{O}}_{{\mathcal{C}}}(-\unicode[STIX]{x1D70F})/{\mathcal{O}}_{{\mathcal{C}}}(-2\unicode[STIX]{x1D70F})),\end{eqnarray}$$
where
 $\unicode[STIX]{x1D70B}:{\mathcal{C}}\rightarrow \overline{{\mathcal{H}}}_{1,2}(7/10)\times {\mathcal{W}}{\mathcal{C}}_{r-1}$
is the universal family,
$\unicode[STIX]{x1D70B}:{\mathcal{C}}\rightarrow \overline{{\mathcal{H}}}_{1,2}(7/10)\times {\mathcal{W}}{\mathcal{C}}_{r-1}$
is the universal family,
![]() $\unicode[STIX]{x1D70E}$
corresponds to one of the universal sections over
$\unicode[STIX]{x1D70E}$
corresponds to one of the universal sections over
 $\overline{{\mathcal{H}}}_{1,2}(7/10)$
, and
$\overline{{\mathcal{H}}}_{1,2}(7/10)$
, and
![]() $\unicode[STIX]{x1D70F}$
corresponds to the universal section over
$\unicode[STIX]{x1D70F}$
corresponds to the universal section over
![]() ${\mathcal{W}}{\mathcal{C}}_{r-1}$
. If
${\mathcal{W}}{\mathcal{C}}_{r-1}$
. If
 ${\mathcal{V}}\subset [V({\mathcal{E}})/\mathbb{G}_{m}]$
is the open locus parameterizing sproutings which do not introduce an elliptic bridge, then
${\mathcal{V}}\subset [V({\mathcal{E}})/\mathbb{G}_{m}]$
is the open locus parameterizing sproutings which do not introduce an elliptic bridge, then
![]() ${\mathcal{V}}$
is the complement of the sub-bundle
${\mathcal{V}}$
is the complement of the sub-bundle
 $[V(\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{{\mathcal{C}}}(-\unicode[STIX]{x1D70F}))/\mathbb{G}_{m}]\subset [V({\mathcal{E}})/\mathbb{G}_{m}]$
. Since
$[V(\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{{\mathcal{C}}}(-\unicode[STIX]{x1D70F}))/\mathbb{G}_{m}]\subset [V({\mathcal{E}})/\mathbb{G}_{m}]$
. Since
 $\overline{{\mathcal{H}}}_{1,2}(7/10)\times {\mathcal{W}}{\mathcal{C}}_{r-1}$
admits a good moduli space, and
$\overline{{\mathcal{H}}}_{1,2}(7/10)\times {\mathcal{W}}{\mathcal{C}}_{r-1}$
admits a good moduli space, and
 $V({\mathcal{E}})\backslash V(\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{{\mathcal{C}}}(-\unicode[STIX]{x1D70F}))$
is affine over
$V({\mathcal{E}})\backslash V(\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{{\mathcal{C}}}(-\unicode[STIX]{x1D70F}))$
is affine over
 $\overline{{\mathcal{H}}}_{1,2}(7/10)\times {\mathcal{W}}{\mathcal{C}}_{r-1}$
, we have that
$\overline{{\mathcal{H}}}_{1,2}(7/10)\times {\mathcal{W}}{\mathcal{C}}_{r-1}$
, we have that
![]() ${\mathcal{V}}$
admits a good moduli space. By Lemma 4.2, there is an induced morphism
${\mathcal{V}}$
admits a good moduli space. By Lemma 4.2, there is an induced morphism
 $\unicode[STIX]{x1D6F9}:{\mathcal{V}}\rightarrow \overline{{\mathcal{M}}}_{2r,1}(2/3).$
The image of
$\unicode[STIX]{x1D6F9}:{\mathcal{V}}\rightarrow \overline{{\mathcal{M}}}_{2r,1}(2/3).$
The image of
![]() $\unicode[STIX]{x1D6F9}$
is
$\unicode[STIX]{x1D6F9}$
is
![]() ${\mathcal{W}}{\mathcal{C}}_{r}$
, and
${\mathcal{W}}{\mathcal{C}}_{r}$
, and
![]() $\unicode[STIX]{x1D6F9}$
is finite by Proposition 4.7. Thus, Proposition 1.4 implies that
$\unicode[STIX]{x1D6F9}$
is finite by Proposition 4.7. Thus, Proposition 1.4 implies that
![]() ${\mathcal{W}}{\mathcal{C}}_{r}$
admits a good moduli space.◻
${\mathcal{W}}{\mathcal{C}}_{r}$
admits a good moduli space.◻
For higher
![]() $(g,n)$
, we can use gluing maps to decompose
$(g,n)$
, we can use gluing maps to decompose
 $\overline{{\mathcal{H}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
into products of lower-dimensional moduli spaces.
$\overline{{\mathcal{H}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
into products of lower-dimensional moduli spaces.
Lemma 4.13. Let
 $\unicode[STIX]{x1D6FC}_{c}\in \{9/11,7/10,2/3\}$
. There exist finite gluing morphisms
$\unicode[STIX]{x1D6FC}_{c}\in \{9/11,7/10,2/3\}$
. There exist finite gluing morphisms
 $$\begin{eqnarray}\unicode[STIX]{x1D6F9}:\overline{{\mathcal{M}}}_{g_{1},n_{1}+1}(\unicode[STIX]{x1D6FC}_{c})\times \overline{{\mathcal{M}}}_{g_{2},n_{2}+1}(\unicode[STIX]{x1D6FC}_{c})\rightarrow \overline{{\mathcal{M}}}_{g_{1}+g_{2},n_{1}+n_{2}}(\unicode[STIX]{x1D6FC}_{c})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}:\overline{{\mathcal{M}}}_{g_{1},n_{1}+1}(\unicode[STIX]{x1D6FC}_{c})\times \overline{{\mathcal{M}}}_{g_{2},n_{2}+1}(\unicode[STIX]{x1D6FC}_{c})\rightarrow \overline{{\mathcal{M}}}_{g_{1}+g_{2},n_{1}+n_{2}}(\unicode[STIX]{x1D6FC}_{c})\end{eqnarray}$$
obtained by identifying
 $(C,\{p_{i}\}_{i=1}^{n_{1}+1})$
and
$(C,\{p_{i}\}_{i=1}^{n_{1}+1})$
and
 $(C^{\prime },\{p_{i}^{\prime }\}_{i=1}^{n_{2}+1})$
nodally at
$(C^{\prime },\{p_{i}^{\prime }\}_{i=1}^{n_{2}+1})$
nodally at
 $p_{n_{1}+1}\sim p_{n_{2}+1}^{\prime }$
.
$p_{n_{1}+1}\sim p_{n_{2}+1}^{\prime }$
.
Proof. The morphism
![]() $\unicode[STIX]{x1D6F9}$
is well defined by Lemma 4.1. To see that
$\unicode[STIX]{x1D6F9}$
is well defined by Lemma 4.1. To see that
![]() $\unicode[STIX]{x1D6F9}$
is finite, first observe that
$\unicode[STIX]{x1D6F9}$
is finite, first observe that
![]() $\unicode[STIX]{x1D6F9}$
is clearly representable and quasi-finite. Furthermore, since the limit of a disconnecting node is a disconnecting node in
$\unicode[STIX]{x1D6F9}$
is clearly representable and quasi-finite. Furthermore, since the limit of a disconnecting node is a disconnecting node in
 $\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
[Reference Alper, Fedorchuk, Smyth and van der WyckAFSvdW17, Corollary 2.11],
$\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
[Reference Alper, Fedorchuk, Smyth and van der WyckAFSvdW17, Corollary 2.11],
![]() $\unicode[STIX]{x1D6F9}$
satisfies the valuative criterion for properness.◻
$\unicode[STIX]{x1D6F9}$
satisfies the valuative criterion for properness.◻
In the case
 $\unicode[STIX]{x1D6FC}_{c}=7/10$
, we will need two additional gluing morphisms.
$\unicode[STIX]{x1D6FC}_{c}=7/10$
, we will need two additional gluing morphisms.
Lemma 4.14. There exist finite gluing morphisms
 $$\begin{eqnarray}\overline{{\mathcal{M}}}_{g,n+2}(7/10)\times {\mathcal{E}}{\mathcal{C}}_{r}\rightarrow \overline{{\mathcal{M}}}_{g+2r,n}(7/10),\quad {\mathcal{E}}{\mathcal{C}}_{r}\rightarrow \overline{{\mathcal{M}}}_{2r}(7/10),\end{eqnarray}$$
$$\begin{eqnarray}\overline{{\mathcal{M}}}_{g,n+2}(7/10)\times {\mathcal{E}}{\mathcal{C}}_{r}\rightarrow \overline{{\mathcal{M}}}_{g+2r,n}(7/10),\quad {\mathcal{E}}{\mathcal{C}}_{r}\rightarrow \overline{{\mathcal{M}}}_{2r}(7/10),\end{eqnarray}$$
where the first map is obtained by nodally gluing
 $(C,\{p_{i}\}_{i=1}^{n+2})$
and an elliptic chain
$(C,\{p_{i}\}_{i=1}^{n+2})$
and an elliptic chain
 $(Z,q_{1},q_{2})$
at
$(Z,q_{1},q_{2})$
at
 $p_{n+1}\sim q_{1}$
and
$p_{n+1}\sim q_{1}$
and
 $p_{n+2}\sim q_{2}$
, and the second map is obtained by nodally self-gluing an elliptic chain
$p_{n+2}\sim q_{2}$
, and the second map is obtained by nodally self-gluing an elliptic chain
 $(Z,q_{1},q_{2})$
at
$(Z,q_{1},q_{2})$
at
![]() $q_{1}\sim q_{2}$
.
$q_{1}\sim q_{2}$
.
Proposition 4.15. Let
 $\unicode[STIX]{x1D6FC}_{c}\in \{9/11,7/10,2/3\}$
and suppose that
$\unicode[STIX]{x1D6FC}_{c}\in \{9/11,7/10,2/3\}$
and suppose that
 $\overline{{\mathcal{M}}}_{g^{\prime },n^{\prime }}(\unicode[STIX]{x1D6FC}_{c})$
admits a proper good moduli space for all
$\overline{{\mathcal{M}}}_{g^{\prime },n^{\prime }}(\unicode[STIX]{x1D6FC}_{c})$
admits a proper good moduli space for all
![]() $(g^{\prime },n^{\prime })$
satisfying
$(g^{\prime },n^{\prime })$
satisfying
![]() $g^{\prime }<g$
. Then
$g^{\prime }<g$
. Then
 $\overline{{\mathcal{H}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
admits a proper good moduli space.
$\overline{{\mathcal{H}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
admits a proper good moduli space.
Proof. Let
 $\unicode[STIX]{x1D6FC}_{c}=9/11$
. By Lemma 4.11, we may assume that
$\unicode[STIX]{x1D6FC}_{c}=9/11$
. By Lemma 4.11, we may assume that
 $(g,n)\neq (1,1)$
. By Lemma 4.13, there exists a finite gluing morphism
$(g,n)\neq (1,1)$
. By Lemma 4.13, there exists a finite gluing morphism
 $$\begin{eqnarray}\unicode[STIX]{x1D6F9}:\overline{{\mathcal{M}}}_{g-1,n+1}(9/11)\times \overline{{\mathcal{H}}}_{1,1}(9/11)\rightarrow \overline{{\mathcal{M}}}_{g,n}(9/11),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}:\overline{{\mathcal{M}}}_{g-1,n+1}(9/11)\times \overline{{\mathcal{H}}}_{1,1}(9/11)\rightarrow \overline{{\mathcal{M}}}_{g,n}(9/11),\end{eqnarray}$$
whose image is precisely
 $\overline{{\mathcal{H}}}_{g,n}(9/11)$
. Now
$\overline{{\mathcal{H}}}_{g,n}(9/11)$
. Now
 $\overline{{\mathcal{H}}}_{g,n}(9/11)$
admits a proper good moduli space by Proposition 1.4.
$\overline{{\mathcal{H}}}_{g,n}(9/11)$
admits a proper good moduli space by Proposition 1.4.
Let
 $\unicode[STIX]{x1D6FC}_{c}=7/10$
. For every
$\unicode[STIX]{x1D6FC}_{c}=7/10$
. For every
![]() $r$
such that
$r$
such that
 $\overline{{\mathcal{M}}}_{g-2r,n+2}(7/10)$
(respectively,
$\overline{{\mathcal{M}}}_{g-2r,n+2}(7/10)$
(respectively,
 $\overline{{\mathcal{M}}}_{g-2r-1,n}(7/10)$
) exists, Lemma 4.14 (respectively, Lemma 4.13) gives a finite gluing morphism
$\overline{{\mathcal{M}}}_{g-2r-1,n}(7/10)$
) exists, Lemma 4.14 (respectively, Lemma 4.13) gives a finite gluing morphism
 $$\begin{eqnarray}\displaystyle & \displaystyle \overline{{\mathcal{M}}}_{g-2r,n+2}(7/10)\times {\mathcal{E}}{\mathcal{C}}_{r}\rightarrow \overline{{\mathcal{H}}}_{g,n}(7/10) & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\text{respectively, }\overline{{\mathcal{M}}}_{g-2r-1,n}(7/10)\times {\mathcal{E}}{\mathcal{C}}_{r}\rightarrow \overline{{\mathcal{H}}}_{g,n}(7/10)) & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \overline{{\mathcal{M}}}_{g-2r,n+2}(7/10)\times {\mathcal{E}}{\mathcal{C}}_{r}\rightarrow \overline{{\mathcal{H}}}_{g,n}(7/10) & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\text{respectively, }\overline{{\mathcal{M}}}_{g-2r-1,n}(7/10)\times {\mathcal{E}}{\mathcal{C}}_{r}\rightarrow \overline{{\mathcal{H}}}_{g,n}(7/10)) & \displaystyle \nonumber\end{eqnarray}$$
that identifies
 $(C,\{p_{i}\}_{i=1}^{n+2})$
(respectively,
$(C,\{p_{i}\}_{i=1}^{n+2})$
(respectively,
 $(C,\{p_{i}\}_{i=1}^{n})$
) to
$(C,\{p_{i}\}_{i=1}^{n})$
) to
 $(Z,q_{1},q_{2})$
at
$(Z,q_{1},q_{2})$
at
 $p_{n+1}\sim q_{1}$
,
$p_{n+1}\sim q_{1}$
,
 $p_{n+2}\sim q_{2}$
(respectively,
$p_{n+2}\sim q_{2}$
(respectively,
![]() $p_{n}\sim q_{1}$
). In addition, for every triple of integers
$p_{n}\sim q_{1}$
). In addition, for every triple of integers
 $(i,m,r)$
such that the stack
$(i,m,r)$
such that the stack
 $\overline{{\mathcal{M}}}_{i,m+1}(7/10)\times \overline{{\mathcal{M}}}_{g-i-2r+1,n-m+1}(7/10)$
is defined, Lemma 4.13 gives a finite gluing morphism
$\overline{{\mathcal{M}}}_{i,m+1}(7/10)\times \overline{{\mathcal{M}}}_{g-i-2r+1,n-m+1}(7/10)$
is defined, Lemma 4.13 gives a finite gluing morphism
 $$\begin{eqnarray}\displaystyle \overline{{\mathcal{M}}}_{i,m+1}(7/10)\times \overline{{\mathcal{M}}}_{g-i-2r+1,n-m+1}(7/10)\times {\mathcal{E}}{\mathcal{C}}_{r}\rightarrow \overline{{\mathcal{H}}}_{g,n}(7/10), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \overline{{\mathcal{M}}}_{i,m+1}(7/10)\times \overline{{\mathcal{M}}}_{g-i-2r+1,n-m+1}(7/10)\times {\mathcal{E}}{\mathcal{C}}_{r}\rightarrow \overline{{\mathcal{H}}}_{g,n}(7/10), & & \displaystyle \nonumber\end{eqnarray}$$
which identifies
 $(C,\{p_{i}\}_{i=1}^{m+1})$
,
$(C,\{p_{i}\}_{i=1}^{m+1})$
,
 $(C^{\prime },\{p_{i}^{\prime }\}_{i=1}^{n-m+1})$
,
$(C^{\prime },\{p_{i}^{\prime }\}_{i=1}^{n-m+1})$
,
 $(Z,q_{1},q_{2})$
nodally at
$(Z,q_{1},q_{2})$
nodally at
 $p_{m+1}\sim q_{1}$
,
$p_{m+1}\sim q_{1}$
,
 $p_{n-m+1}^{\prime }\sim q_{2}$
. Finally, if
$p_{n-m+1}^{\prime }\sim q_{2}$
. Finally, if
 $(g,n)=(2r,0)$
, Lemma 4.14 gives a finite gluing morphism
$(g,n)=(2r,0)$
, Lemma 4.14 gives a finite gluing morphism
 $$\begin{eqnarray}\displaystyle {\mathcal{E}}{\mathcal{C}}_{r}\rightarrow \overline{{\mathcal{H}}}_{2r}(7/10), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{E}}{\mathcal{C}}_{r}\rightarrow \overline{{\mathcal{H}}}_{2r}(7/10), & & \displaystyle \nonumber\end{eqnarray}$$
which nodally self-glues
 $(Z,q_{1},q_{2})$
at
$(Z,q_{1},q_{2})$
at
![]() $q_{1}\sim q_{2}$
. The union of these gluing morphisms covers
$q_{1}\sim q_{2}$
. The union of these gluing morphisms covers
 $\overline{{\mathcal{H}}}_{g,n}(7/10)$
. Thus,
$\overline{{\mathcal{H}}}_{g,n}(7/10)$
. Thus,
 $\overline{{\mathcal{H}}}_{g,n}(7/10)$
admits a proper good moduli space by Proposition 1.4 and Lemma 4.12.
$\overline{{\mathcal{H}}}_{g,n}(7/10)$
admits a proper good moduli space by Proposition 1.4 and Lemma 4.12.
Let
 $\unicode[STIX]{x1D6FC}_{c}=2/3$
. By Lemma 4.11, we may assume that
$\unicode[STIX]{x1D6FC}_{c}=2/3$
. By Lemma 4.11, we may assume that
 $(g,n)\neq (2,1)$
. For each
$(g,n)\neq (2,1)$
. For each
 $r=1,\ldots ,\lfloor g/2\rfloor$
, Lemma 4.13 provides a finite gluing morphism
$r=1,\ldots ,\lfloor g/2\rfloor$
, Lemma 4.13 provides a finite gluing morphism
 $$\begin{eqnarray}\overline{{\mathcal{M}}}_{g-2r,n+1}(2/3)\times {\mathcal{W}}{\mathcal{C}}_{r}(2/3)\rightarrow \overline{{\mathcal{M}}}_{g,n}(2/3)\end{eqnarray}$$
$$\begin{eqnarray}\overline{{\mathcal{M}}}_{g-2r,n+1}(2/3)\times {\mathcal{W}}{\mathcal{C}}_{r}(2/3)\rightarrow \overline{{\mathcal{M}}}_{g,n}(2/3)\end{eqnarray}$$
(if
 $r=g/2$
and
$r=g/2$
and
![]() $n=1$
, we consider
$n=1$
, we consider
 $\overline{{\mathcal{M}}}_{g-2r,n+1}(2/3)$
as the empty set). The union of these gluing morphisms covers
$\overline{{\mathcal{M}}}_{g-2r,n+1}(2/3)$
as the empty set). The union of these gluing morphisms covers
 $\overline{{\mathcal{H}}}_{g,n}(2/3)$
. Now
$\overline{{\mathcal{H}}}_{g,n}(2/3)$
. Now
 $\overline{{\mathcal{H}}}_{g,n}(2/3)$
admits a proper good moduli space by Proposition 1.4 and Lemma 4.12.◻
$\overline{{\mathcal{H}}}_{g,n}(2/3)$
admits a proper good moduli space by Proposition 1.4 and Lemma 4.12.◻
4.4 Existence for
 $\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC})$
$\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC})$
Proof of Theorem 1.1.
Fix
 $\unicode[STIX]{x1D6FC}_{c}\in \{9/11,7/10,2/3\}$
. Note that
$\unicode[STIX]{x1D6FC}_{c}\in \{9/11,7/10,2/3\}$
. Note that
 $\overline{{\mathcal{M}}}_{0,n}(\unicode[STIX]{x1D6FC}_{c})=\overline{{\mathcal{M}}}_{0,n}$
, so
$\overline{{\mathcal{M}}}_{0,n}(\unicode[STIX]{x1D6FC}_{c})=\overline{{\mathcal{M}}}_{0,n}$
, so
 $\overline{{\mathcal{M}}}_{0,n}(\unicode[STIX]{x1D6FC}_{c})$
admits a proper good moduli space for all
$\overline{{\mathcal{M}}}_{0,n}(\unicode[STIX]{x1D6FC}_{c})$
admits a proper good moduli space for all
![]() $n$
. By induction on
$n$
. By induction on
![]() $g$
, we may assume that
$g$
, we may assume that
 $\overline{{\mathcal{M}}}_{g^{\prime },n^{\prime }}(\unicode[STIX]{x1D6FC}_{c})$
admits a proper good moduli space for all
$\overline{{\mathcal{M}}}_{g^{\prime },n^{\prime }}(\unicode[STIX]{x1D6FC}_{c})$
admits a proper good moduli space for all
![]() $(g^{\prime },n^{\prime })$
with
$(g^{\prime },n^{\prime })$
with
![]() $g^{\prime }<g$
. Note that
$g^{\prime }<g$
. Note that
 $\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC})=\overline{{\mathcal{M}}}_{g,n}$
for
$\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC})=\overline{{\mathcal{M}}}_{g,n}$
for
 $\unicode[STIX]{x1D6FC}>9/11$
. By descending induction on
$\unicode[STIX]{x1D6FC}>9/11$
. By descending induction on
![]() $\unicode[STIX]{x1D6FC}$
, we may now assume that
$\unicode[STIX]{x1D6FC}$
, we may now assume that
 $\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC})$
admits a good moduli space for all
$\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC})$
admits a good moduli space for all
 $\unicode[STIX]{x1D6FC}\geqslant \unicode[STIX]{x1D6FC}_{c}+\unicode[STIX]{x1D716}$
. By [Reference Alper, Fedorchuk, Smyth and van der WyckAFSvdW17, Theorem 3.17], the inclusions
$\unicode[STIX]{x1D6FC}\geqslant \unicode[STIX]{x1D6FC}_{c}+\unicode[STIX]{x1D716}$
. By [Reference Alper, Fedorchuk, Smyth and van der WyckAFSvdW17, Theorem 3.17], the inclusions
 $\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D716}){\hookrightarrow}\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}){\hookleftarrow}\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D716})$
arise from local VGIT with respect to
$\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D716}){\hookrightarrow}\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}){\hookleftarrow}\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D716})$
arise from local VGIT with respect to
![]() $\unicode[STIX]{x1D6FF}-\unicode[STIX]{x1D713}$
, and Propositions 4.15 and 4.10 imply that
$\unicode[STIX]{x1D6FF}-\unicode[STIX]{x1D713}$
, and Propositions 4.15 and 4.10 imply that
 $\overline{{\mathcal{H}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})=\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})\setminus \overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c}-\unicode[STIX]{x1D716})$
and
$\overline{{\mathcal{H}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})=\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})\setminus \overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c}-\unicode[STIX]{x1D716})$
and
 $\overline{{\mathcal{S}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})=\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})\setminus \overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c}+\unicode[STIX]{x1D716})$
admit proper good moduli spaces. Now Theorem 1.3 implies that
$\overline{{\mathcal{S}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})=\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})\setminus \overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c}+\unicode[STIX]{x1D716})$
admit proper good moduli spaces. Now Theorem 1.3 implies that
 $\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
and
$\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c})$
and
 $\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c}-\unicode[STIX]{x1D716})$
admit proper good moduli spaces fitting into the stated diagram.◻
$\overline{{\mathcal{M}}}_{g,n}(\unicode[STIX]{x1D6FC}_{c}-\unicode[STIX]{x1D716})$
admit proper good moduli spaces fitting into the stated diagram.◻
Acknowledgements
We thank Brendan Hassett, Johan de Jong, Ian Morrison, and Ravi Vakil for many useful conversations and suggestions. During the preparation of this paper, the first author was partially supported by the Australian Research Council grant DE140101519 and by a Humboldt Fellowship. The second author was partially supported by NSF grant DMS-1259226, a Sloan Research Fellowship, and the Australian National University MSRVP fund. The third author was partially supported by the Australian Research Council grant DE140100259.
Appendix A
In this appendix, we give examples of algebraic stacks including moduli stacks of curves which fail to have a good moduli space owing to a failure of conditions (1a), (1b), and (2) in Theorem 1.2. Note that there is an obviously necessary topological condition for a stack to admit a good moduli space, namely that every
![]() $k$
-point has a unique isotrivial specialization to a closed point, and each of our examples satisfies this condition. The purpose of these examples is to illustrate the more subtle kinds of stacky behavior that can obstruct the existence of good moduli spaces.
$k$
-point has a unique isotrivial specialization to a closed point, and each of our examples satisfies this condition. The purpose of these examples is to illustrate the more subtle kinds of stacky behavior that can obstruct the existence of good moduli spaces.
We work over an algebraically closed field of characteristic 0.
A.1 Failure of condition (1a) in Theorem 1.2
Example A.1. Let
 ${\mathcal{X}}=[X/\mathbb{Z}_{2}]$
be the quotient stack, where
${\mathcal{X}}=[X/\mathbb{Z}_{2}]$
be the quotient stack, where
![]() $X$
is the non-separated affine line and
$X$
is the non-separated affine line and
![]() $\mathbb{Z}_{2}$
acts on
$\mathbb{Z}_{2}$
acts on
![]() $X$
by swapping the origins and fixing all other points. The algebraic stack clearly satisfies conditions (1b) and (2). Then there is an étale, affine morphism
$X$
by swapping the origins and fixing all other points. The algebraic stack clearly satisfies conditions (1b) and (2). Then there is an étale, affine morphism
 $\mathbb{A}^{1}\rightarrow {\mathcal{X}}$
which is stabilizer preserving at the origin but is not stabilizer preserving in an open neighborhood. The algebraic stack
$\mathbb{A}^{1}\rightarrow {\mathcal{X}}$
which is stabilizer preserving at the origin but is not stabilizer preserving in an open neighborhood. The algebraic stack
![]() ${\mathcal{X}}$
does not admit a good moduli space.
${\mathcal{X}}$
does not admit a good moduli space.
While the above example may appear entirely pathological, we now provide two natural moduli stacks similar to this example.
Example A.2. Consider the Deligne–Mumford locus
 ${\mathcal{X}}\subset [\operatorname{Sym}^{4}\mathbb{P}^{1}/\operatorname{PGL}_{2}]$
of unordered tuples
${\mathcal{X}}\subset [\operatorname{Sym}^{4}\mathbb{P}^{1}/\operatorname{PGL}_{2}]$
of unordered tuples
 $(p_{1},p_{2},p_{3},p_{4})$
, where at least three points are distinct. Consider the family
$(p_{1},p_{2},p_{3},p_{4})$
, where at least three points are distinct. Consider the family
 $(0,1,\unicode[STIX]{x1D706},\infty )$
with
$(0,1,\unicode[STIX]{x1D706},\infty )$
with
![]() $\unicode[STIX]{x1D706}\in \mathbb{P}^{1}$
. When
$\unicode[STIX]{x1D706}\in \mathbb{P}^{1}$
. When
 $\unicode[STIX]{x1D706}\notin \{0,1,\infty \}$
,
$\unicode[STIX]{x1D706}\notin \{0,1,\infty \}$
,
 $\operatorname{Aut}(0,1,\unicode[STIX]{x1D706},\infty )\cong \mathbb{Z}/2\mathbb{Z}\times \mathbb{Z}/2\mathbb{Z}$
; indeed, if
$\operatorname{Aut}(0,1,\unicode[STIX]{x1D706},\infty )\cong \mathbb{Z}/2\mathbb{Z}\times \mathbb{Z}/2\mathbb{Z}$
; indeed, if
 $\unicode[STIX]{x1D70E}\in \operatorname{PGL}_{2}$
is the unique element such that
$\unicode[STIX]{x1D70E}\in \operatorname{PGL}_{2}$
is the unique element such that
 $\unicode[STIX]{x1D70E}(0)=\infty$
,
$\unicode[STIX]{x1D70E}(0)=\infty$
,
 $\unicode[STIX]{x1D70E}(\infty )=0$
, and
$\unicode[STIX]{x1D70E}(\infty )=0$
, and
 $\unicode[STIX]{x1D70E}(1)=\unicode[STIX]{x1D706}$
, then
$\unicode[STIX]{x1D70E}(1)=\unicode[STIX]{x1D706}$
, then
 $\unicode[STIX]{x1D70E}([x,y])=[y,\unicode[STIX]{x1D706}x]$
, so that
$\unicode[STIX]{x1D70E}([x,y])=[y,\unicode[STIX]{x1D706}x]$
, so that
 $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D706})=1$
and therefore
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D706})=1$
and therefore
 $\unicode[STIX]{x1D70E}\in \operatorname{Aut}(0,1,\unicode[STIX]{x1D706},\infty )$
. Similarly, there is an element which acts via
$\unicode[STIX]{x1D70E}\in \operatorname{Aut}(0,1,\unicode[STIX]{x1D706},\infty )$
. Similarly, there is an element which acts via
![]() $0\leftrightarrow 1$
,
$0\leftrightarrow 1$
,
![]() $\unicode[STIX]{x1D706}\leftrightarrow \infty$
and an element which acts via
$\unicode[STIX]{x1D706}\leftrightarrow \infty$
and an element which acts via
![]() $0\leftrightarrow \unicode[STIX]{x1D706}$
,
$0\leftrightarrow \unicode[STIX]{x1D706}$
,
![]() $1\leftrightarrow \infty$
. However, if
$1\leftrightarrow \infty$
. However, if
 $\unicode[STIX]{x1D706}\in \{0,1,\infty \}$
, then
$\unicode[STIX]{x1D706}\in \{0,1,\infty \}$
, then
 $\operatorname{Aut}(0,1,\unicode[STIX]{x1D706},\infty )\cong \mathbb{Z}/2\mathbb{Z}$
.
$\operatorname{Aut}(0,1,\unicode[STIX]{x1D706},\infty )\cong \mathbb{Z}/2\mathbb{Z}$
.
Therefore, any étale neighborhood
 $f:[\operatorname{Spec}A/\mathbb{Z}_{2}]\rightarrow {\mathcal{X}}$
of
$f:[\operatorname{Spec}A/\mathbb{Z}_{2}]\rightarrow {\mathcal{X}}$
of
 $x=(0,1,\infty ,\infty )$
will be stabilizer preserving at
$x=(0,1,\infty ,\infty )$
will be stabilizer preserving at
![]() $x$
but not in any open neighborhood. This failure of condition (1a) here is due to the fact that automorphisms of the generic fiber do not extend to the special fiber. The algebraic stack
$x$
but not in any open neighborhood. This failure of condition (1a) here is due to the fact that automorphisms of the generic fiber do not extend to the special fiber. The algebraic stack
![]() ${\mathcal{X}}$
does not admit a good moduli space but we note that if one enlarges the stack
${\mathcal{X}}$
does not admit a good moduli space but we note that if one enlarges the stack
![]() ${\mathcal{X}}$
to
${\mathcal{X}}$
to
 $[(\operatorname{Sym}^{4}\mathbb{P}^{1})^{ss}/\operatorname{PGL}_{2}]$
by including the point
$[(\operatorname{Sym}^{4}\mathbb{P}^{1})^{ss}/\operatorname{PGL}_{2}]$
by including the point
 $(0,0,\infty ,\infty )$
, there does exist a good moduli space.
$(0,0,\infty ,\infty )$
, there does exist a good moduli space.
Example A.3. Let
![]() ${\mathcal{V}}_{2}$
be the stack of all reduced, connected curves of genus 2, and let
${\mathcal{V}}_{2}$
be the stack of all reduced, connected curves of genus 2, and let
 $[C]\in {\mathcal{V}}_{2}$
denote a cuspidal curve whose pointed normalization is a generic one-pointed smooth elliptic curve
$[C]\in {\mathcal{V}}_{2}$
denote a cuspidal curve whose pointed normalization is a generic one-pointed smooth elliptic curve
![]() $(E,p)$
. We will show that any Deligne–Mumford open neighborhood
$(E,p)$
. We will show that any Deligne–Mumford open neighborhood
 ${\mathcal{M}}\subset {\mathcal{V}}_{2}$
of
${\mathcal{M}}\subset {\mathcal{V}}_{2}$
of
![]() $[C]$
is non-separated and fails to satisfy condition (1a).
$[C]$
is non-separated and fails to satisfy condition (1a).
Note that
 $\operatorname{Aut}(C)=\operatorname{Aut}(E,p)=\mathbb{Z}/2\mathbb{Z}$
. Thus, to show that no étale neighborhood
$\operatorname{Aut}(C)=\operatorname{Aut}(E,p)=\mathbb{Z}/2\mathbb{Z}$
. Thus, to show that no étale neighborhood
 $$\begin{eqnarray}[\operatorname{Def}(C)/\text{Aut}(C)]\rightarrow {\mathcal{M}}\end{eqnarray}$$
$$\begin{eqnarray}[\operatorname{Def}(C)/\text{Aut}(C)]\rightarrow {\mathcal{M}}\end{eqnarray}$$
can be stabilizer preserving where
 $\operatorname{Def}(C)=\operatorname{Spec}A$
is an
$\operatorname{Def}(C)=\operatorname{Spec}A$
is an
![]() $\operatorname{Aut}(C)$
-equivariant algebraized miniversal deformation space, it is sufficient to exhibit a family
$\operatorname{Aut}(C)$
-equivariant algebraized miniversal deformation space, it is sufficient to exhibit a family
![]() ${\mathcal{C}}\rightarrow \unicode[STIX]{x1D6E5}$
whose special fiber is
${\mathcal{C}}\rightarrow \unicode[STIX]{x1D6E5}$
whose special fiber is
![]() $C$
and whose generic fiber has automorphism group
$C$
and whose generic fiber has automorphism group
 $\mathbb{Z}/2\mathbb{Z}\times \mathbb{Z}/2\mathbb{Z}$
. To do this, let
$\mathbb{Z}/2\mathbb{Z}\times \mathbb{Z}/2\mathbb{Z}$
. To do this, let
![]() $C^{\prime }$
be the curve obtained by nodally gluing two identical copies of
$C^{\prime }$
be the curve obtained by nodally gluing two identical copies of
![]() $(E,p)$
along their respective marked points. Then
$(E,p)$
along their respective marked points. Then
![]() $C^{\prime }$
admits an involution swapping the two components, and a corresponding degree-2 map
$C^{\prime }$
admits an involution swapping the two components, and a corresponding degree-2 map
 $C^{\prime }\rightarrow E$
ramified over the single point
$C^{\prime }\rightarrow E$
ramified over the single point
![]() $p$
. We may smooth
$p$
. We may smooth
![]() $C^{\prime }$
to a family
$C^{\prime }$
to a family
 ${\mathcal{C}}^{\prime }\rightarrow \unicode[STIX]{x1D6E5}$
of smooth double covers of
${\mathcal{C}}^{\prime }\rightarrow \unicode[STIX]{x1D6E5}$
of smooth double covers of
![]() $E$
, simply by separating the ramification points. By [Reference SmythSmy11a, Lemma 2.12], there exists a birational contraction
$E$
, simply by separating the ramification points. By [Reference SmythSmy11a, Lemma 2.12], there exists a birational contraction
![]() ${\mathcal{C}}^{\prime }\rightarrow {\mathcal{C}}$
contracting one of the two copies of
${\mathcal{C}}^{\prime }\rightarrow {\mathcal{C}}$
contracting one of the two copies of
![]() $E$
in the central fiber to a cusp. The family
$E$
in the central fiber to a cusp. The family
![]() ${\mathcal{C}}\rightarrow \unicode[STIX]{x1D6E5}$
now has the desired properties; the generic fiber has both a hyperelliptic and a bi-elliptic involution while the central fiber is
${\mathcal{C}}\rightarrow \unicode[STIX]{x1D6E5}$
now has the desired properties; the generic fiber has both a hyperelliptic and a bi-elliptic involution while the central fiber is
![]() $C$
.
$C$
.
A.2 Failure of condition (1b) in Theorem 1.2
Example A.4. Let
 ${\mathcal{X}}=[(\mathbb{A}^{2}\setminus 0)/\mathbb{G}_{m}]$
, where
${\mathcal{X}}=[(\mathbb{A}^{2}\setminus 0)/\mathbb{G}_{m}]$
, where
![]() $\mathbb{G}_{m}$
acts via
$\mathbb{G}_{m}$
acts via
 $t\cdot (x,y)=(x,ty)$
. Let
$t\cdot (x,y)=(x,ty)$
. Let
 ${\mathcal{U}}=\{y\neq 0\}\subset {\mathcal{X}}$
. Observe that the point
${\mathcal{U}}=\{y\neq 0\}\subset {\mathcal{X}}$
. Observe that the point
![]() $(0,1)$
is closed in
$(0,1)$
is closed in
![]() ${\mathcal{U}}$
and
${\mathcal{U}}$
and
![]() ${\mathcal{X}}$
. Then the open immersion
${\mathcal{X}}$
. Then the open immersion
 $f:{\mathcal{U}}\rightarrow {\mathcal{X}}$
has the property that
$f:{\mathcal{U}}\rightarrow {\mathcal{X}}$
has the property that
 $f(0,1)\in {\mathcal{X}}$
is closed while, for
$f(0,1)\in {\mathcal{X}}$
is closed while, for
![]() $x\neq 0$
, the point
$x\neq 0$
, the point
 $(x,1)\in {\mathcal{U}}$
is closed but
$(x,1)\in {\mathcal{U}}$
is closed but
 $f(x,1)\in {\mathcal{X}}$
is not closed. In other words,
$f(x,1)\in {\mathcal{X}}$
is not closed. In other words,
 $f:{\mathcal{U}}\rightarrow {\mathcal{X}}$
does not send closed points to closed points and, in fact, there is no étale neighborhood
$f:{\mathcal{U}}\rightarrow {\mathcal{X}}$
does not send closed points to closed points and, in fact, there is no étale neighborhood
 ${\mathcal{W}}\rightarrow {\mathcal{X}}$
of
${\mathcal{W}}\rightarrow {\mathcal{X}}$
of
![]() $(0,1)$
which sends closed points to closed points. The algebraic stack
$(0,1)$
which sends closed points to closed points. The algebraic stack
![]() ${\mathcal{X}}$
does not admit a good moduli space.
${\mathcal{X}}$
does not admit a good moduli space.
Example A.5. Let
 ${\mathcal{M}}=\overline{{\mathcal{M}}}_{g}\cup {\mathcal{M}}^{1}\cup {\mathcal{M}}^{2}$
, where
${\mathcal{M}}=\overline{{\mathcal{M}}}_{g}\cup {\mathcal{M}}^{1}\cup {\mathcal{M}}^{2}$
, where
![]() ${\mathcal{M}}^{1}$
consists of all curves of arithmetic genus
${\mathcal{M}}^{1}$
consists of all curves of arithmetic genus
![]() $g$
with a single cusp and smooth normalization, and
$g$
with a single cusp and smooth normalization, and
![]() ${\mathcal{M}}^{2}$
consists of all curves of the form
${\mathcal{M}}^{2}$
consists of all curves of the form
![]() $D\cup E_{0}$
, where
$D\cup E_{0}$
, where
![]() $D$
is a smooth curve of genus
$D$
is a smooth curve of genus
![]() $g-1$
and
$g-1$
and
![]() $E_{0}$
is a rational cuspidal curve attached to
$E_{0}$
is a rational cuspidal curve attached to
![]() $C$
nodally.
$C$
nodally.
We observe that
![]() ${\mathcal{M}}$
has the following property: if
${\mathcal{M}}$
has the following property: if
 $C=D\cup E$
, where
$C=D\cup E$
, where
![]() $D$
is a curve of genus
$D$
is a curve of genus
![]() $g-1$
and
$g-1$
and
![]() $E$
is an elliptic tail, then
$E$
is an elliptic tail, then
 $[C]\in {\mathcal{M}}$
is a closed point if and only if
$[C]\in {\mathcal{M}}$
is a closed point if and only if
![]() $D$
is singular. Indeed, if
$D$
is singular. Indeed, if
![]() $D$
is smooth, then
$D$
is smooth, then
![]() $C$
admits an isotrivial specialization to
$C$
admits an isotrivial specialization to
![]() $D\cup E_{0}$
, where
$D\cup E_{0}$
, where
![]() $E_{0}$
is a rational cuspidal tail. Now consider any curve of the form
$E_{0}$
is a rational cuspidal tail. Now consider any curve of the form
 $C=D\cup E$
, where
$C=D\cup E$
, where
![]() $D$
is a singular curve of genus
$D$
is a singular curve of genus
![]() $g-1$
and
$g-1$
and
![]() $E$
is a smooth elliptic tail and, for simplicity, assume that
$E$
is a smooth elliptic tail and, for simplicity, assume that
![]() $D$
has no automorphisms. We claim that there is no étale neighborhood of the form
$D$
has no automorphisms. We claim that there is no étale neighborhood of the form
 $[\operatorname{Def}(C)/\text{Aut}(C)]\rightarrow {\mathcal{M}}$
which sends closed points to closed points. Indeed, curves of the form
$[\operatorname{Def}(C)/\text{Aut}(C)]\rightarrow {\mathcal{M}}$
which sends closed points to closed points. Indeed, curves of the form
![]() $D^{\prime }\cup E$
where
$D^{\prime }\cup E$
where
![]() $D^{\prime }$
is smooth will appear in any such neighborhood and will obviously be closed in
$D^{\prime }$
is smooth will appear in any such neighborhood and will obviously be closed in
 $[\operatorname{Def}(C)/\text{Aut}(C)]$
(since this is a Deligne–Mumford stack), but are not closed in
$[\operatorname{Def}(C)/\text{Aut}(C)]$
(since this is a Deligne–Mumford stack), but are not closed in
![]() ${\mathcal{M}}$
.
${\mathcal{M}}$
.
A.3 Failure of condition (2) in Theorem 1.2
Example A.6. Let
 ${\mathcal{X}}=[X/\mathbb{G}_{m}]$
, where
${\mathcal{X}}=[X/\mathbb{G}_{m}]$
, where
![]() $X$
is the nodal cubic curve with the
$X$
is the nodal cubic curve with the
![]() $\mathbb{G}_{m}$
-action given by multiplication. Observe that
$\mathbb{G}_{m}$
-action given by multiplication. Observe that
![]() ${\mathcal{X}}$
is an algebraic stack with two points: one open and one closed. But
${\mathcal{X}}$
is an algebraic stack with two points: one open and one closed. But
![]() ${\mathcal{X}}$
does not admit a good moduli space; if it did,
${\mathcal{X}}$
does not admit a good moduli space; if it did,
![]() ${\mathcal{X}}$
would necessarily be cohomologically affine and consequently
${\mathcal{X}}$
would necessarily be cohomologically affine and consequently
![]() $X$
would be affine, which is a contradiction. However, there is an étale and affine (but not finite) morphism
$X$
would be affine, which is a contradiction. However, there is an étale and affine (but not finite) morphism
 ${\mathcal{W}}=[\operatorname{Spec}(k[x,y]/xy)/\mathbb{G}_{m}]\rightarrow {\mathcal{X}}$
, where
${\mathcal{W}}=[\operatorname{Spec}(k[x,y]/xy)/\mathbb{G}_{m}]\rightarrow {\mathcal{X}}$
, where
 $\mathbb{G}_{m}=\operatorname{Spec}k[t,t^{-1}]$
acts on
$\mathbb{G}_{m}=\operatorname{Spec}k[t,t^{-1}]$
acts on
 $\operatorname{Spec}k[x,y]/xy$
via
$\operatorname{Spec}k[x,y]/xy$
via
 $t\cdot (x,y)=(tx,t^{-1}y)$
, which is stabilizer preserving and sends closed points to closed points; however, the two projections
$t\cdot (x,y)=(tx,t^{-1}y)$
, which is stabilizer preserving and sends closed points to closed points; however, the two projections
 ${\mathcal{W}}\times _{{\mathcal{X}}}{\mathcal{W}}\rightrightarrows {\mathcal{W}}$
do not send closed points to closed points.
${\mathcal{W}}\times _{{\mathcal{X}}}{\mathcal{W}}\rightrightarrows {\mathcal{W}}$
do not send closed points to closed points.
To realize this étale local presentation concretely, we may express
 $X=Y/\mathbb{Z}_{2}$
, where
$X=Y/\mathbb{Z}_{2}$
, where
![]() $Y$
is the union of two irreducible rational curves with coordinates
$Y$
is the union of two irreducible rational curves with coordinates
![]() $[x_{1},y_{1}]$
and
$[x_{1},y_{1}]$
and
![]() $[x_{2},y_{2}]$
glued via nodes at
$[x_{2},y_{2}]$
glued via nodes at
 $p=0_{1}=0_{2}$
and
$p=0_{1}=0_{2}$
and
 $q=\infty _{1}=\infty _{2}$
by the action of
$q=\infty _{1}=\infty _{2}$
by the action of
![]() $\mathbb{Z}/2\mathbb{Z}$
, where
$\mathbb{Z}/2\mathbb{Z}$
, where
![]() $-1$
acts via
$-1$
acts via
 $[x_{1},y_{1}]\leftrightarrow [y_{2},x_{2}]$
. There is a
$[x_{1},y_{1}]\leftrightarrow [y_{2},x_{2}]$
. There is a
![]() $\mathbb{G}_{m}$
-action on
$\mathbb{G}_{m}$
-action on
![]() $Y$
given by
$Y$
given by
 $t\cdot [x_{1},y_{1}]=[tx_{1},y_{1}]$
and
$t\cdot [x_{1},y_{1}]=[tx_{1},y_{1}]$
and
 $t\cdot [x_{2},y_{2}]=[x_{1},ty_{1}]$
, which descends to the
$t\cdot [x_{2},y_{2}]=[x_{1},ty_{1}]$
, which descends to the
![]() $\mathbb{G}_{m}$
-action on
$\mathbb{G}_{m}$
-action on
![]() $X$
. There is a finite étale morphism
$X$
. There is a finite étale morphism
 $[Y/\mathbb{G}_{m}]\rightarrow {\mathcal{X}}$
, but
$[Y/\mathbb{G}_{m}]\rightarrow {\mathcal{X}}$
, but
![]() $[Y/\mathbb{G}_{m}]$
is not cohomologically affine. If we instead consider the open substack
$[Y/\mathbb{G}_{m}]$
is not cohomologically affine. If we instead consider the open substack
 ${\mathcal{W}}=[(Y\setminus \{p\})/\mathbb{G}_{m}]$
, then
${\mathcal{W}}=[(Y\setminus \{p\})/\mathbb{G}_{m}]$
, then
 ${\mathcal{W}}\cong [\operatorname{Spec}(k[x,y]/xy)/\mathbb{G}_{m}]$
is cohomologically affine and there is an étale representable morphism
${\mathcal{W}}\cong [\operatorname{Spec}(k[x,y]/xy)/\mathbb{G}_{m}]$
is cohomologically affine and there is an étale representable morphism
 $f:{\mathcal{W}}\rightarrow {\mathcal{X}}$
. It is easy to see that
$f:{\mathcal{W}}\rightarrow {\mathcal{X}}$
. It is easy to see that
 $$\begin{eqnarray}{\mathcal{W}}\times _{{\mathcal{X}}}{\mathcal{W}}\cong [(Y\setminus \{p\})/\mathbb{G}_{m}]\coprod [(Y\setminus \{p,q\})/\mathbb{G}_{m}].\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{W}}\times _{{\mathcal{X}}}{\mathcal{W}}\cong [(Y\setminus \{p\})/\mathbb{G}_{m}]\coprod [(Y\setminus \{p,q\})/\mathbb{G}_{m}].\end{eqnarray}$$
But
 $[(Y\setminus \{p,q\})/\mathbb{G}_{m}]\cong \operatorname{Spec}k\coprod \operatorname{Spec}k$
and the projections
$[(Y\setminus \{p,q\})/\mathbb{G}_{m}]\cong \operatorname{Spec}k\coprod \operatorname{Spec}k$
and the projections
 $p_{1},p_{2}:{\mathcal{W}}\times _{{\mathcal{X}}}{\mathcal{W}}\rightarrow {\mathcal{W}}$
correspond to the inclusion of the two open points into
$p_{1},p_{2}:{\mathcal{W}}\times _{{\mathcal{X}}}{\mathcal{W}}\rightarrow {\mathcal{W}}$
correspond to the inclusion of the two open points into
![]() ${\mathcal{W}}$
, which clearly do not send closed points to closed points.
${\mathcal{W}}$
, which clearly do not send closed points to closed points.
Example A.7. Consider the algebraic stack
![]() ${\mathcal{M}}_{g}^{ss,1}$
of Deligne–Mumford semistable curves
${\mathcal{M}}_{g}^{ss,1}$
of Deligne–Mumford semistable curves
![]() $C$
, where any rational subcurve connected to
$C$
, where any rational subcurve connected to
![]() $C$
at only two points is smooth. Let
$C$
at only two points is smooth. Let
![]() $D_{0}$
be the Deligne–Mumford semistable curve
$D_{0}$
be the Deligne–Mumford semistable curve
![]() $D\cup \mathbb{P}^{1}$
, obtained by gluing a
$D\cup \mathbb{P}^{1}$
, obtained by gluing a
![]() $\mathbb{P}^{1}$
to a smooth genus
$\mathbb{P}^{1}$
to a smooth genus
![]() $g-1$
curve
$g-1$
curve
![]() $D$
at two points
$D$
at two points
![]() $p,q$
. For simplicity, let us assume that
$p,q$
. For simplicity, let us assume that
 $\operatorname{Aut}(D,\{p,q\})=0$
, so
$\operatorname{Aut}(D,\{p,q\})=0$
, so
 $\operatorname{Aut}(D_{0})=\mathbb{G}_{m}$
. There is a unique isomorphism class of curves which isotrivially specializes to
$\operatorname{Aut}(D_{0})=\mathbb{G}_{m}$
. There is a unique isomorphism class of curves which isotrivially specializes to
![]() $D_{0}$
, namely the nodal curve
$D_{0}$
, namely the nodal curve
![]() $D_{1}$
obtained by gluing
$D_{1}$
obtained by gluing
![]() $D$
at
$D$
at
![]() $p$
and
$p$
and
![]() $q$
. Thus,
$q$
. Thus,
![]() $\overline{\{[D_{1}]\}}$
has two points: one open and one closed. In fact,
$\overline{\{[D_{1}]\}}$
has two points: one open and one closed. In fact,
![]() $\overline{\{[D_{1}]\}}$
is isomorphic to the quotient stack
$\overline{\{[D_{1}]\}}$
is isomorphic to the quotient stack
![]() $[X/\mathbb{G}_{m}]$
considered in Example A.6.
$[X/\mathbb{G}_{m}]$
considered in Example A.6.