Hostname: page-component-848d4c4894-r5zm4 Total loading time: 0 Render date: 2024-06-23T10:30:14.419Z Has data issue: false hasContentIssue false
  • English
  • Français

Relative cubulations and groups with a 2-sphere boundary

Part of: Special aspects of infinite or finite groups

Published online by Cambridge University Press:  24 March 2020

Eduard Einstein  and
Daniel Groves
Eduard Einstein
Affiliation:
Department of Mathematics, Statistics, and Computer Science, University of Illinois at Chicago, Chicago, IL60607-7045, USA email einstein@uic.edu
Daniel Groves
Affiliation:
Department of Mathematics, Statistics, and Computer Science, University of Illinois at Chicago, Chicago, IL60607-7045, USA email groves@math.uic.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce a new kind of action of a relatively hyperbolic group on a 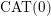$\text{CAT}(0)$ cube complex, called a relatively geometric action. We provide an application to characterize finite-volume Kleinian groups in terms of actions on cube complexes, analogous to the results of Markovic and Haïssinsky in the closed case.

Keywords

relatively hyperbolic groupscube complexesboundaries

MSC classification

Primary: 20F65: Geometric group theory
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 4 , April 2020 , pp. 862 - 867
Copyright
© The Authors 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The second author was partially supported by the National Science Foundation, DMS-1507067.

References

Agol, I., The virtual Haken conjecture, Doc. Math. 18 (2013), 1045–1087; with an appendix by Agol, Daniel Groves, and Jason Manning.Google Scholar
Agol, I., Groves, D. and Manning, J. F., Residual finiteness, QCERF and fillings of hyperbolic groups, Geom. Topol. 13 (2009), 1043–1073.CrossRefGoogle Scholar
Agol, I., Groves, D. and Manning, J. F., An alternate proof of Wise’s malnormal special quotient theorem, Forum Math. Pi 4 (2016), E1.CrossRefGoogle Scholar
Bergeron, N. and Wise, D. T., A boundary criterion for cubulation, Amer. J. Math. 134 (2012), 843–859.CrossRefGoogle Scholar
Cannon, J. W., The theory of negatively curved spaces and groups, in Ergodic theory, symbolic dynamics, and hyperbolic spaces (Trieste, 1989) (Oxford University Press, New York, 1991), 315–369.Google Scholar
Cannon, J. W. and Swenson, E. L., Recognizing constant curvature discrete groups in dimension 3, Trans. Amer. Math. Soc. 350 (1998), 809–849.CrossRefGoogle Scholar
Charney, R. and Crisp, J., Relative hyperbolicity and Artin groups, Geom. Dedicata 129 (2007), 1–13.CrossRefGoogle Scholar
Cooper, D. and Futer, D., Ubiquitous quasi-Fuchsian surfaces in cusped hyperbolic 3-manifolds, Geom. Topol. 23 (2019), 241–298.CrossRefGoogle Scholar
Groves, D. and Manning, J. F., Dehn filling in relatively hyperbolic groups, Israel J. Math. 168 (2008), 317–429.CrossRefGoogle Scholar
Groves, D. and Manning, J. F., Quasiconvexity and Dehn filling, Amer. J. Math., to appear. Preprint (2017), arXiv:1708.07968.Google Scholar
Groves, D. and Manning, J. F., Hyperbolic groups acting improperly, Preprint (2018), arXiv:1808.02325.Google Scholar
Groves, D., Manning, J. F. and Sisto, A., Boundaries of Dehn fillings, Geom. Topol. 23 (2019), 2929–3002.CrossRefGoogle Scholar
Haglund, F. and Wise, D. T., A combination theorem for special cube complexes, Ann. of Math. (2) 176 (2012), 1427–1482.CrossRefGoogle Scholar
Haïssinsky, P., Hyperbolic groups with planar boundaries, Invent. Math. 201 (2015), 239–307.CrossRefGoogle Scholar
Hruska, G. C., Relative hyperbolicity and relative quasiconvexity for countable groups, Algebr. Geom. Topol. 10 (2010), 1807–1856.CrossRefGoogle Scholar
Hruska, G. C. and Wise, D. T., Finiteness properties of cubulated groups, Compos. Math. 150 (2014), 453–506.CrossRefGoogle Scholar
Hsu, T. and Wise, D. T., Cubulating malnormal amalgams, Invent. Math. 199 (2015), 293–331.CrossRefGoogle Scholar
Kahn, J. and Markovic, V., Immersing almost geodesic surfaces in a closed hyperbolic three manifold, Ann. of Math. (2) 175 (2012), 1127–1190.CrossRefGoogle Scholar
Kapovich, M., Problems on boundaries of groups and Kleinian groups, https://www.math.ucdavis.edu/∼kapovich/EPR/problems.pdf, 2007.Google Scholar
Markovic, V., Criterion for Cannon’s conjecture, Geom. Funct. Anal. 23 (2013), 1035–1061.CrossRefGoogle Scholar
Sageev, M., Codimension-1 subgroups and splittings of groups, J. Algebra 189 (1997), 377–389.CrossRefGoogle Scholar
Sageev, M. and Wise, D. T., Cores for quasiconvex actions, Proc. Amer. Math. Soc. 143 (2015), 2731–2741.CrossRefGoogle Scholar
Wise, D. T., The structure of groups with a quasiconvex hierarchy, Ann. of Math. Stud., to appear.Google Scholar
Yaman, A., A topological characterisation of relatively hyperbolic groups, J. Reine Angew. Math. 566 (2004), 41–89.Google Scholar