Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-20T02:22:07.844Z Has data issue: false hasContentIssue false
  • English
  • Français

A Plancherel formula for Sp2n/Spn×Spn and its application

Part of: Discontinuous groups and automorphic forms Abstract harmonic analysis

Published online by Cambridge University Press:  01 March 2009

Zhengyu Mao  and
Stephen Rallis
Zhengyu Mao
Affiliation:
Department of Mathematics and Computer Science, Rutgers University, Newark, NJ 07102-1811, USA (email: zmao@rutgers.edu)
Stephen Rallis
Affiliation:
Department of Mathematics, The Ohio State University, Columbus, OH 43210, USA (email: haar@math.ohio-state.edu)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We compute the spherical functions on the symmetric space Sp2n/Spn×Spn and derive a Plancherel formula for functions on the symmetric space. As an application of the Plancherel formula, we prove an identity which amounts to the fundamental lemma of a relative trace identity between Sp2n and .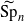

Keywords

spherical functionMacdonald polynomialPlancherel formula

MSC classification

Secondary: 43A90: Spherical functions 11F72: Spectral theory; Selberg trace formula
Type
Research Article
Information
Compositio Mathematica , Volume 145 , Issue 2 , March 2009 , pp. 501 - 527
Copyright
Copyright © Foundation Compositio Mathematica 2009

References

[1]Bump, D., Friedberg, S. and Hoffstein, J., p-adic Whittaker functions on the metaplectic group, Duke Math. J. 63 (1991), 379–397.CrossRefGoogle Scholar
[2]Casselman, W., The unramified principal series of p-adic groups I: the spherical function, Compositio Math. 40 (1980), 387–406.Google Scholar
[3]Casselman, W. and Shalika, J., The unramified principal series of p-adic groups II: the Whittaker function, Compositio Math. 41 (1980), 207–231.Google Scholar
[4]Ginzburg, D., Rallis, S. and Soudry, D., On a correspondence between cuspidal representations of GL 2n and , J. Amer. Math. Soc. 12 (1999), 849–907.CrossRefGoogle Scholar
[5]Ginzburg, D., Rallis, S. and Soudry, D., Lifting csup froms on GL 2n to : the unramified correspondence, Duke Math. J. 100 (1999), 243–266.CrossRefGoogle Scholar
[6]Hironaka, Y., Spherical functions and local densities on hermitian forms, J. Math. Soc. Japan 51 (1999), 553–581.CrossRefGoogle Scholar
[7]Hironaka, Y. and Sato, F., Spherical functions and local densities of alternating forms, Amer. J. Math. 110 (1988), 473–512.CrossRefGoogle Scholar
[8]Macdonald, I. G., Orthogonal polynomials associated with root systems, Sém. Lothar. Combin. 45 (2000), Article B45a.Google Scholar
[9]Macdonald, I. G., Spherical functions on a group of p-adic type, Publications of Ramanujan Institute No. 2 (Ramanujan Institute, Centre for Advanced Study in Mathematics, University of Madras, 1971).Google Scholar
[10]Mao, Z. and Rallis, S., A relative trace identity for GL 2n and , Preprint.Google Scholar
[11]Offen, O., Relative spherical functions on p-adic symmetric spaces (three cases), Pacific J. Math. 215 (2004), 97–149.CrossRefGoogle Scholar
[12]Offen, O., Correction to “Relative spherical functions on p-adic symmetric spaces (three cases)”, Pacific J. Math 236 (2008), 195–200.CrossRefGoogle Scholar