Hostname: page-component-8448b6f56d-cfpbc Total loading time: 0 Render date: 2024-04-24T05:25:19.865Z Has data issue: false hasContentIssue false
  • English
  • Français

On fields of rationality for automorphic representations

Part of: Algebraic number theory: local and $p$-adic fields Algebraic number theory: global fields Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  11 September 2014

Sug Woo Shin  and
Nicolas Templier
Sug Woo Shin
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA Korea Institute for Advanced Study, 85 Hoegiro, Dongdaemun-gu, Seoul 130-722, Republic of Korea email swshin@math.mit.edu
Nicolas Templier
Affiliation:
Department of Mathematics, Princeton University, Princeton, NJ 08544, USA email templier@math.princeton.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper proves two results on the field of rationality 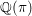$\mathbb{Q}({\it\pi})$ for an automorphic representation ${\it\pi}$, which is the subfield of 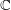$\mathbb{C}$ fixed under the subgroup of 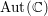$\text{Aut}(\mathbb{C})$ stabilizing the isomorphism class of the finite part of ${\it\pi}$. For general linear groups and classical groups, our first main result is the finiteness of the set of discrete automorphic representations ${\it\pi}$ such that ${\it\pi}$ is unramified away from a fixed finite set of places, 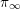${\it\pi}_{\infty }$ has a fixed infinitesimal character, and 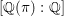$[\mathbb{Q}({\it\pi}):\mathbb{Q}]$ is bounded. The second main result is that for classical groups, 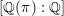$[\mathbb{Q}({\it\pi}):\mathbb{Q}]$ grows to infinity in a family of automorphic representations in level aspect whose infinite components are discrete series in a fixed 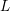$L$-packet under mild conditions.

Keywords

field of rationalityautomorphic representationsGalois representationsfiniteness

MSC classification

Primary: 11F30: Fourier coefficients of automorphic forms 11F70: Representation-theoretic methods; automorphic representations over local and global fields 11F80: Galois representations 11R39: Langlands-Weil conjectures, nonabelian class field theory 11S37: Langlands-Weil conjectures, nonabelian class field theory
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 12 , December 2014 , pp. 2003 - 2053
Copyright
© The Author(s) 2014 

References

Anderson, G., Blasius, D., Coleman, R. and Zettler, G., On representations of the Weil group with bounded conductor, Forum Math. 6 (1994), 537–545.Google Scholar
Arthur, J., Orthogonal and symplectic groups, in The endoscopic classification of representations, American Mathematical Society Colloquium Publications, vol. 61 (American Mathematical Society, Providence, RI, 2013).Google Scholar
Barnet-Lamb, T., Gee, T., Geraghty, D. and Taylor, R., Local–global compatibility for l = p. II, Ann. Sci. Éc. Norm. Supér. (4) 47 (2014), 165–179.Google Scholar
Bergeron, N., Millson, J. and Moeglin, C., Hodge type theorems for arithmetic manifolds associated to orthogonal groups, Ann. of Math. (2), submitted. Preprint (2011),arXiv:1110.3049.Google Scholar
Blasius, D., Harris, M. and Ramakrishnan, D., Coherent cohomology, limits of discrete series, and Galois conjugation, Duke Math. J. 73 (1994), 647–685.Google Scholar
Borel, A., Automorphic L-functions, in Automorphic forms, representations and L-functions (Oregon State University, Corvallis, OR, 1977, Part 2), Proceedings of Symposia in Pure Mathematics, vol. XXXIII (American Mathematical Society, Providence, RI, 1979), 27–61.Google Scholar
Borel, A., Automorphic forms on reductive groups, in Automorphic forms and applications, IAS/Park City Mathematics Series, vol. 12 (American Mathematical Society, Providence, RI, 2007), 7–39.Google Scholar
Buzzard, K. and Gee, T., The conjectural connections between automorphic representations and Galois representations, in Proc. LMS Durham Symp. (2011), to appear. Preprint (2010),arXiv:1009.0785.Google Scholar
Calegari, F. and Emerton, M., The Hecke algebra T khas large index, Math. Res. Lett. 11 (2004), 125–137.CrossRefGoogle Scholar
Caraiani, A., Monodromy and local–global compatibility for $l=p$, Preprint (2012),arXiv:1202:4683.Google Scholar
Caraiani, A., Local–global compatibility and the action of monodromy on nearby cycles, Duke Math. J. 161 (2012), 2311–2413.Google Scholar
Chenevier, G. and Harris, M., Construction of automorphic Galois representations, II, Cambridge Math. J. 1 (2013), 53–73.Google Scholar
Clozel, L., Motifs et formes automorphes: applications du principe de fonctorialité, in Automorphic forms, Shimura varieties, and L-functions, Vol. I (Ann Arbor, MI, 1988, Perspectives in Mathematics, vol. 10 (Academic Press, Boston, MA, 1990), 77–159.Google Scholar
Clozel, L., Purity reigns supreme, Int. Math. Res. Not. IMRN (2013), 328–346.Google Scholar
Deitmar, A. and Hoffman, W., Spectral estimates for towers of noncompact quotients, Canad. J. Math. 51 (1999), 266–293.Google Scholar
Deligne, P., Théorie de Hodge. I, in Actes du Congrès International des Mathématiciens (Nice, 1970), Tome 1 (Gauthier-Villars, Paris, 1971), 425–430.Google Scholar
Duke, W. and Kowalski, E., A problem of Linnik for elliptic curves and mean-value estimates for automorphic representations, Invent. Math. 139 (2000), 1–39; with an appendix by Dinakar Ramakrishnan.CrossRefGoogle Scholar
Elkies, N. D., Howe, E. W. and Ritzenthaler, C., Genus bounds for curves with fixed Frobenius eigenvalues, Proc. Amer. Math. Soc. 142 (2014), 71–84.Google Scholar
Ellenberg, J. S. and Venkatesh, A., Reflection principles and bounds for class group torsion, Int. Math. Res. Not. IMRN 2007 (2007), doi:10.1093/imrn/rnm002.Google Scholar
Faltings, G., Finiteness theorems for abelian varieties over number fields, in Arithmetic geometry (Storrs, CT, 1984) (Springer, New York, 1986), 9–27; translated from the German original [Invent. Math. 73 (1983, no. 3, 349–366; Invent. Math. 75 (1984), no. 2, 381; MR 85g:11026ab] by Edward Shipz.CrossRefGoogle Scholar
Flath, D., Decomposition of representations into tensor products, in Proceedings of Symposia in Pure Mathematics, vol. 33(1) (American Mathematical Society, Providence, RI, 1979), 179–183.Google Scholar
Fontaine, J.-M. and Mazur, B., Geometric Galois representations, in Elliptic curves, modular forms, & Fermat’s last theorem (Hong Kong, 1993), Series in Number Theory, vol. I (International Press, Cambridge, MA, 1995), 41–78.Google Scholar
Franke, J. and Schwermer, J., A decomposition of spaces of automorphic forms, and the Eisenstein cohomology of arithmetic groups, Math. Ann. 311 (1998), 765–790.CrossRefGoogle Scholar
Gamburd, A., Jakobson, D. and Sarnak, P., Spectra of elements in the group ring of SU(2), J. Eur. Math. Soc. (JEMS) 1 (1999), 51–85.Google Scholar
Gross, B. H., Algebraic modular forms, Israel J. Math. 113 (1999), 61–93.Google Scholar
Gross, B. H. and Rohrlich, D. E., Some results on the Mordell–Weil group of the Jacobian of the Fermat curve, Invent. Math. 44 (1978), 201–224.Google Scholar
Harish-Chandra, Automorphic forms on semisimple Lie groups. Notes by J. G. M. Mars, Lecture Notes in Mathematics, vol. 62(Springer, Berlin, 1968).Google Scholar
Harris, M. and Taylor, R., The geometry and cohomology of some simple Shimura varieties, Annals of Mathematics Studies, vol. 151 (Princeton University Press, Princeton, NJ, 2001); with an appendix by Vladimir G. Berkovich.Google Scholar
Helfgott, H. A. and Venkatesh, A., Integral points on elliptic curves and 3-torsion in class groups, J. Amer. Math. Soc. 19 (2006), 527–550; (electronic).CrossRefGoogle Scholar
Henniart, G., Une preuve simple des conjectures de Langlands pour GL(n) sur un corpsp-adiques, Invent. Math. 139 (2000), 439–455.Google Scholar
Hida, H., Hecke fields of analytic families of modular forms, J. Amer. Math. Soc. 24 (2011), 51–80.Google Scholar
Hida, H., A finiteness property of abelian varieties with potentially ordinary good reduction, J. Amer. Math. Soc. 25 (2012), 813–826.Google Scholar
Khare, C., Conjectures on finiteness of mod p Galois representations, J. Ramanujan Math. Soc. 15 (2000), 23–42.Google Scholar
Kim, H. H. and Krishnamurthy, M., Stable base change lift from unitary groups to GLn, IMRP Int. Math. Res. Pap. 1 (2005), 1–52.Google Scholar
Kottwitz, R. E. and Shelstad, D., Foundations of twisted endoscopy, Astérisque (1999), vi+190.Google Scholar
Labesse, J.-P., Changement de base CM et séries discrètes, in On the stabilization of the trace formula, The Stable Trace Formula, Shimura Varieties, and Arithmetic Applications, vol. 1 (International Press, Somerville, MA, 2011), 429–470.Google Scholar
Langlands, R., The classification of representations of real reductive groups, Mathematics Surveys and Monographs, vol. 31 (American Mathematical Society, Providence, RI, 1988).Google Scholar
Langlands, R. and Shelstad, D., On the definition of transfer factors, Math. Ann. 278 (1987), 219–271.Google Scholar
Madan, M. L. and Madden, D. J., Note on class groups of algebraic function fields, J. Reine Angew. Math. 295 (1977), 57–60.Google Scholar
Milne., J. S., Abelian varieties, in Arithmetic geometry (Storrs, CT, 1984) (Springer, New York, 1986), 103–150.Google Scholar
Moeglin, C., Classification et changement de base pour les séries discrètes des groupes unitaires padiques, Pacific J. Math. 233 (2007), 159–204.Google Scholar
Mok, C. P., Endoscopic classification of representations of quasi-split unitary groups, Mem. Amer. Math. Soc., to appear. Preprint (2012), arXiv:1206.0882.Google Scholar
Ngô., B. C., Le lemme fondamental pour les algèbres de Lie, Publ. Math. Inst. Hautes Études Sci. (2010), 1–169.Google Scholar
Patrikis, S., Variations on a theorem of Tate, Preprint (2012), arXiv:1207.6724v1 [math.NT].Google Scholar
Rohlfs, J. and Speh, B., On limit multiplicities of representations with cohomology in the cuspidal spectrum, Duke Math. 55 (1987), 199–211.CrossRefGoogle Scholar
Royer, E., Facteurs Q-simples de J 0(N) de grande dimension et de grand rang, Bull. Soc. Math. France 128 (2000), 219–248.Google Scholar
Saito, T., Weight spectral sequences and independence of l, J. Inst. Math. Jussieu 2 (2003), 583–634.CrossRefGoogle Scholar
Sarnak, P., Maass cusp forms with integer coefficients, in A panorama of number theory or the view from Baker’s garden (Zürich, 1999) (Cambridge University Press, Cambridge, 2002), 121–127.CrossRefGoogle Scholar
Sauvageot, F., Principe de densité pour les groupes réductifs, Compositio Math. 108 (1997), 151–184.Google Scholar
Scholze, P., Perfectoid spaces, Publ. Math. Inst. Hautes Études Sci. 116 (2012), 245–313.Google Scholar
Schwermer, J., Geometric cycles, arithmetic groups and their cohomology, Bull. Amer. Math. Soc. (N.S.) 47 (2010), 187–279.Google Scholar
Serre, J.-P., Linear representations of finite groups, Graduate Texts in Mathematics, vol. 42 (Springer, New York, 1977), translated from the second French edition by Leonard L. Scott.Google Scholar
Serre, J.-P., Local fields, Graduate Texts in Mathematics, vol. 67 (Springer, New York, 1979), translated from the French by Marvin Jay Greenberg.Google Scholar
Serre, J.-P., Répartition asymptotique des valeurs propres de l’opérateur de Hecke T p, J. Amer. Math. Soc. 10 (1997), 75–102.Google Scholar
Serre, J.-P., Bounds for the orders of the finite subgroups of G (k), in Group representation theory (EPFL Press, Lausanne, 2007), 405–450.Google Scholar
Shin, S. W., Galois representations arising from some compact Shimura varieties, Ann. of Math. (2) 173 (2011), 1645–1741.CrossRefGoogle Scholar
Shin, S. W., Automorphic Plancherel density theorem, Israel J. Math. 192 (2012), 83–120.Google Scholar
Shin, S.-W. and Templier, N., Sato–Tate theorem for families and low-lying zeros of automorphic L-functions, submitted, 129pp, with Appendix A by R. Kottwitz and Appendix B by R. Cluckers, J. Gordon and I. Halupczok. Preprint (2012), arXiv:1208.1945.Google Scholar
Taylor, R., Galois representations, Ann. Fac. Sci. Toulouse 13 (2004), 73–119.Google Scholar
Taylor, R. and Yoshida, T., Compatibility of local and global Langlands correspondences, J. Amer. Math. Soc. 20 (2007), 467–493.CrossRefGoogle Scholar
Vaaler, J. D., Some extremal functions in Fourier analysis, Bull. Amer. Math. Soc. (N.S.) 12 (1985), 183–216.Google Scholar
Vogan, D. A. Jr, The local Langlands conjecture, in Representation theory of groups and algebras, Contemporary Mathematics, vol. 145 (American Mathematical Society, Providence, RI, 1993), 305–379.Google Scholar
Waldspurger, J.-L., Quelques propriétés arithmétiques de certaines formes automorphes sur GL(2), Compositio Math. 54 (1985), 121–171.Google Scholar
Waldspurger, J.-L., Le lemme fondamental implique le transfert, Compositio Math. 105 (1997), 153–236.Google Scholar
Waldspurger, J.-L., La formule de Plancherel pour les groupes p-adiques d’après Harish-Chandra, J. Inst. Math. Jussieu 2 (2003), 235–333.Google Scholar
Waldspurger, J.-L., Endoscopie et changement de caractéristique, J. Inst. Math. Jussieu 5 (2006), 423–525.Google Scholar
Waldspurger, J.-L., L’endoscopie tordue n’est pas si tordue, Mem. Amer. Math. Soc. 194 (2008), x+261.Google Scholar
Waldspurger, J.-L., Les facteurs de transfert pour les groupes classiques: un formulaire, Manuscripta Math. 133 (2010), 41–82.Google Scholar
Yamada, T., A remark on Schur indices of p-groups, Proc. Amer. Math. Soc. 76 (1979), 45.Google Scholar
Yu, J.-K., Bruhat–Tits theory and buildings, in Ottawa lectures on admissible representations of reductive p-adic groups, Fields Institute Monographs, vol. 26 (American Mathematical Society, Providence, RI, 2009), 53–77.Google Scholar