Article contents
Locality in the Fukaya category of a hyperkähler manifold
Published online by Cambridge University Press: 06 September 2019
Abstract
Let 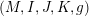 $(M,I,J,K,g)$ be a hyperkähler manifold. Then the complex manifold
$(M,I,J,K,g)$ be a hyperkähler manifold. Then the complex manifold 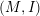 $(M,I)$ is holomorphic symplectic. We prove that for all real
$(M,I)$ is holomorphic symplectic. We prove that for all real 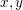 $x,y$, with
$x,y$, with 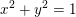 $x^{2}+y^{2}=1$ except countably many, any finite-energy
$x^{2}+y^{2}=1$ except countably many, any finite-energy 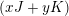 $(xJ+yK)$-holomorphic curve with boundary in a collection of
$(xJ+yK)$-holomorphic curve with boundary in a collection of 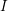 $I$-holomorphic Lagrangians must be constant. By an argument based on the Łojasiewicz inequality, this result holds no matter how the Lagrangians intersect each other. It follows that one can choose perturbations such that the holomorphic polygons of the associated Fukaya category lie in an arbitrarily small neighborhood of the Lagrangians. That is, the Fukaya category is local. We show that holomorphic Lagrangians are tautologically unobstructed. Moreover, the Fukaya
$I$-holomorphic Lagrangians must be constant. By an argument based on the Łojasiewicz inequality, this result holds no matter how the Lagrangians intersect each other. It follows that one can choose perturbations such that the holomorphic polygons of the associated Fukaya category lie in an arbitrarily small neighborhood of the Lagrangians. That is, the Fukaya category is local. We show that holomorphic Lagrangians are tautologically unobstructed. Moreover, the Fukaya 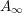 $A_{\infty }$ algebra of a holomorphic Lagrangian is formal. Our result also explains why the special Lagrangian condition holds without instanton corrections for holomorphic Lagrangians.
$A_{\infty }$ algebra of a holomorphic Lagrangian is formal. Our result also explains why the special Lagrangian condition holds without instanton corrections for holomorphic Lagrangians.
Keywords
- Type
- Research Article
- Information
- Copyright
- © The Authors 2019
Footnotes
Current address: Instituto Nacional de Matemática Pura e Aplicada (IMPA), Estrada Dona Castorina, 110, Jardim Botânico, CEP 22460-320, Rio de Janeiro, RJ, Brasil
J.S. was partially supported by ERC starting grant 337560 and ISF Grant 1747/13. M.V. was partially supported by the Russian Academic Excellence Project ‘5-100’ and CNPq - Process 313608/2017-2.
References
- 4
- Cited by


