Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-18T03:21:20.731Z Has data issue: false hasContentIssue false
  • English
  • Français

Integral division points on curves

Part of: Arithmetic algebraic geometry Arithmetic and non-Archimedean dynamical systems Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  09 September 2013

David Grant  and
Su-Ion Ih
David Grant
Affiliation:
Department of Mathematics, University of Colorado at Boulder, Boulder, CO 80309-0395, USA email grant@colorado.edu
Su-Ion Ih
Affiliation:
Department of Mathematics, University of Colorado at Boulder, Boulder, CO 80309-0395, USA email ih@math.colorado.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 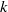$k$ be a number field with algebraic closure 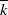$ \overline{k} $, and let 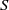$S$ be a finite set of primes of 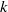$k$ containing all the infinite ones. Let 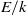$E/ k$ be an elliptic curve, 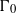${\mit{\Gamma} }_{0} $ be a finitely generated subgroup of 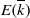$E( \overline{k} )$, and 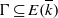$\mit{\Gamma} \subseteq E( \overline{k} )$ the division group attached to 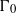${\mit{\Gamma} }_{0} $. Fix an effective divisor 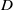$D$ of 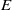$E$ with support containing either: (i) at least two points whose difference is not torsion; or (ii) at least one point not in 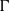$\mit{\Gamma} $. We prove that the set of ‘integral division points on 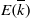$E( \overline{k} )$’, i.e., the set of points of 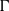$\mit{\Gamma} $ which are 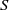$S$-integral on 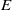$E$ relative to 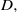$D, $ is finite. We also prove the 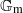${ \mathbb{G} }_{\mathrm{m} } $-analogue of this theorem, thereby establishing the 1-dimensional case of a general conjecture we pose on integral division points on semi-abelian varieties.

Keywords

division groupdivision pointintegral pointprimitive divisorSchinzel’s theoremSiegel’s theorem

MSC classification

Secondary: 11G05: Elliptic curves over global fields 11G35: Varieties over global fields 11G50: Heights 14G05: Rational points 37P05: Polynomial and rational maps 37P35: Arithmetic properties of periodic points
Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 12 , December 2013 , pp. 2011 - 2035
Copyright
© The Author(s) 2013 

References

Baker, M., Ih, S. and Rumely, R., A finiteness property of torsion points, Algebra Number Theory 2 (2008), 217–248.Google Scholar
Cheon, J. and Hahn, S., The orders of the reductions of a point in the Mordell–Weil group of an elliptic curve, Acta Arith. 88 (1999), 219–222.CrossRefGoogle Scholar
Evertse, J.-H., Györy, K., Stewart, C. L. and Tijdeman, R., On S-unit equations in two unknowns, Invent. Math. 92 (1988), 461–477.Google Scholar
Evertse, J.-H., Schlickewei, H. P. and Schmidt, W. M., Linear equations in variables which lie in a multiplicative group, Ann. of Math. (2) 155 (2002), 807–836.Google Scholar
Faltings, G., Diophantine approximation on abelian varieties, Ann. of Math. (2) 133 (1991), 549–576.Google Scholar
Faltings, G., The general case of S. Lang’s conjecture, in Barsotti Symposium in Algebraic Geometry, Abano Terme, 1991, Perspectives in Mathematics, vol. 15 (Academic Press, San Diego, CA, 1994), 175–182.Google Scholar
Hindry, M., Autour d’une conjecture de Serge Lang, Invent. Math. 94 (1988), 575–603.Google Scholar
Hindry, M. and Silverman, J., Diophantine geometry; An introduction, Graduate Texts in Mathematics, vol. 201 (Springer, New York, 2000).Google Scholar
Ih, S., A nondensity property of preperiodic points on Chebyshev dynamical systems, J. Number Theory 131 (2011), 750–780.Google Scholar
Ih, S., A nondensity property of preperiodic points on the projective plane, J. Lond. Math. Soc. (2) 83 (2011), 691–710.Google Scholar
Ih, S. and Tucker, T. J., A finiteness property for preperiodic points of Chebyshev polynomials, Int. J. Number Theory 6 (2010), 1011–1025.CrossRefGoogle Scholar
Kawaguchi, S. and Silverman, J., Dynamics of projective morphisms having identical canonical heights, Proc. Lond. Math. Soc. (3) 95 (2007), 519–544.Google Scholar
Lang, S., Elliptic curves: Diophantine analysis, Grundlehren der Mathematischen Wissenschaften, vol. 231 (Springer-Verlag, Berlin–New York, 1978).Google Scholar
Lang, S., Complex multiplication, Grundlehren der Mathematischen Wissenschaften, vol. 255 (Springer-Verlag, New York, 1983).Google Scholar
McQuillan, M., Division points on semiabelian varieties, Invent. Math. 120 (1995), 575–603.Google Scholar
Petsche, C., S-integral preperiodic points by dynamical systems over number fields, Bull. Lond. Math. Soc. 40 (2008), 749–758.Google Scholar
Petsche, C., Szpiro, L. and Tucker, T., A dynamical pairing between two rational maps, Trans. Amer. Math. Soc. 364 (2012), 1687–1710.Google Scholar
Schinzel, A., Primitive divisors of the expression ${A}^{n} - {B}^{n} $ in algebraic number fields, Crelle 268/269 (1974), 27–33.Google Scholar
Serre, J.-P., Propriétés galoisiennes des points d’ordre fini des courbes elliptiques, Invent. Math. 15 (1972), 259–331.CrossRefGoogle Scholar
Silverman, J., Wieferich’s criterion and the $abc$-conjecture, J. Number Theory 30 (1988), 226–237.Google Scholar
Silverman, J., Integer points, Diophantine approximation, and iteration of rational maps, Duke Math. J. 71 (1993), 793–829.Google Scholar
Silverman, J., Advanced topics in the arithmetic of elliptic curves, Graduate Texts in Mathematics, vol. 151 (Springer-Verlag, New York, 1994).Google Scholar
Silverman, J., The arithmetic of dynamical systems, Graduate Texts in Mathematics, vol. 241 (Springer, New York, 2007).Google Scholar
Sookdeo, V., Integer points in backward orbits, J. Number Theory 131 (2011), 1229–1239.Google Scholar
Streng, M., Divisibility sequences for elliptic curves with complex multiplication, Algebra and Number Theory 2 (2008), 183–208.Google Scholar
Vojta, P., Diophantine approximations and value distribution theory, Lecture Notes in Mathematics, vol. 1239 (Springer-Verlag, New York, 1987).Google Scholar
Vojta, P., Integral points on subvarieties of semiabelian varieties, II, Amer. J. Math. 121 (1999), 283–313.Google Scholar