Hostname: page-component-848d4c4894-r5zm4 Total loading time: 0 Render date: 2024-06-25T13:51:11.111Z Has data issue: false hasContentIssue false
  • English
  • Français

Donaldson–Thomas theory of 𝒜n×P1

Part of: Projective and enumerative geometry

Published online by Cambridge University Press:  18 August 2009

Davesh Maulik  and
Alexei Oblomkov
Davesh Maulik
Affiliation:
Department of Mathematics, Columbia University, New York, NY 10027, USA (email: dmaulik@cpw.math.columbia.edu)
Alexei Oblomkov
Affiliation:
Department of Mathematics, Princeton University, Princeton, NJ 08544, USA (email: oblomkov@math.princeton.edu)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

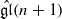We study the relative Donaldson–Thomas theory of 𝒜n×P1, where 𝒜n is the surface resolution of type An singularity. The action of divisor operators in the theory is expressed in terms of operators of the affine algebra on Fock space. Assuming a nondegeneracy conjecture, this gives a complete solution for the theory. The results complete the comparison of this theory with the Gromov–Witten theory of 𝒜n×P1 and the quantum cohomology of the Hilbert scheme of points on 𝒜n.

Keywords

Donaldson–Thomas theoryloop algebrasresolution of quotient surface singularities

MSC classification

Secondary: 14N35: Gromov-Witten invariants, quantum cohomology, Gopakumar-Vafa invariants, Donaldson-Thomas invariants
Type
Research Article
Information
Compositio Mathematica , Volume 145 , Issue 5 , September 2009 , pp. 1249 - 1276
Copyright
Copyright Š Foundation Compositio Mathematica 2009

References

[1]Bryan, J. and Pandharipande, R., The local Gromov–Witten theory of curves, J. Amer. Math. Soc. 21 (2008), 101–136.Google Scholar
[2]Graber, T. and Pandharipande, R., Localization of virtual classes, Invent. Math. 135 (1999), 487–518.CrossRefGoogle Scholar
[3]Grojnowski, I., Instantons and affine algebras. I. The Hilbert scheme and vertex operators, Math. Res. Lett. 3 (1996), 275–291.CrossRefGoogle Scholar
[4]Li, J., Liu, C.-C. M., Liu, K. and Zhou, J., A mathematical theory of the topological vertex, Preprint (2004), math/0408426.Google Scholar
[5]Maulik, D., Gromov–Witten theory of 𝒜n resolutions, Geom. Topol. 13 (2009), 1729–1773.CrossRefGoogle Scholar
[6]Maulik, D., Nekrasov, N., Okounkov, A. and Pandharipande, R., Gromov–Witten theory and Donaldson–Thomas theory I, Compositio Math. 142 (2006), 1263–1285.CrossRefGoogle Scholar
[7]Maulik, D., Nekrasov, N., Okounkov, A. and Pandharipande, R., Gromov–Witten theory and Donaldson–Thomas theory II, Compositio Math. 142 (2006), 1286–1304.CrossRefGoogle Scholar
[8]Maulik, D. and Oblomkov, A., Quantum cohomology of the Hilbert scheme of points on𝒜n-resolutions, J. Amer. Math. Soc. 22 (2009), 1055–1091.CrossRefGoogle Scholar
[9]Maulik, D., Oblomkov, A., Okounkov, A. and Pandharipande, R., GW/DT correspondence for toric threefolds, Preprint (2008), math/0809.3976.Google Scholar
[10]Maulik, D. and Pandharipande, R., A topological view of Gromov–Witten theory, Topology 45 (2006), 887–918.CrossRefGoogle Scholar
[11]Nakajima, H., Heisenberg algebra and Hilbert schemes of points on projective surfaces, Ann. of Math. (2) 145 (1997), 379–388.CrossRefGoogle Scholar
[12]Okounkov, A. and Pandharipande, R., Quantum cohomology of the Hilbert scheme of points in the plane, Preprint (2004), math/0411210.Google Scholar
[13]Okounkov, A. and Pandharipande, R., The local Donaldson–Thomas theory of curves, Preprint (2005), math/0512573.Google Scholar
[14]Pandharipande, R. and Thomas, R., Curve counting via stable pairs in the derived category, Preprint (2007), math/0707.2348.Google Scholar
[15]Qin, Z. and Wang, W., Hilbert schemes of points on the minimal resolution and soliton equations, Contemp. Math. 442 (2007), 435–462.CrossRefGoogle Scholar
[16]Wu, B., The moduli stack of stable relative ideal sheaves, Preprint (2007), math/0701074.Google Scholar