Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-18T01:39:29.170Z Has data issue: false hasContentIssue false
  • English
  • Français

Birational boundedness of low-dimensional elliptic Calabi–Yau varieties with a section

Part of: Surfaces and higher-dimensional varieties Birational geometry

Published online by Cambridge University Press:  21 July 2021

Gabriele Di Cerbo  and
Roberto Svaldi
Gabriele Di Cerbo
Affiliation:
Department of Mathematics, Princeton University, Princeton, NJ08540, USAdicerbo@math.princeton.edu
Roberto Svaldi
Affiliation:
EPFL, SB MATH-GE, MA B1 497 (Bâtiment MA), Station 8, CH-1015Lausanne, Switzerlandroberto.svaldi@epfl.ch
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that there are finitely many families, up to isomorphism in codimension one, of elliptic Calabi–Yau manifolds 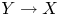$Y\rightarrow X$ with a rational section, provided that 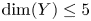$\dim (Y)\leq 5$ and 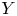$Y$ is not of product type. As a consequence, we obtain that there are finitely many possibilities for the Hodge diamond of such manifolds. The result follows from log birational boundedness of Kawamata log terminal pairs 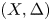$(X, \Delta )$ with 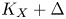$K_X+\Delta$ numerically trivial and not of product type, in dimension at most four.

Keywords

Calabi–Yau varietieslog Calabi–Yau pairsboundedness of algebraic varietieselliptic fibrations

MSC classification

Primary: 14J32: Calabi-Yau manifolds
Secondary: 14E30: Minimal model program (Mori theory, extremal rays) 14J10: Families, moduli, classification 14J81: Relationships with physics
Type
Research Article
Information
Compositio Mathematica , Volume 157 , Issue 8 , August 2021 , pp. 1766 - 1806
Check for updates
Copyright
© 2021 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

G.D.C. is partially supported by the Simons Foundation and NSF grant DMS-1702358. Most of this work was completed during several visits of R.S. to Columbia University. He would like to thank Columbia University for the hospitality and the nice working environment. He would also like to thank MIT where he was a graduate student and UCSD where he was a visitor when part of this work was completed. He kindly acknowledges financial support from NSF research grant nos 1200656 and 1265263 and Churchill College, Cambridge. During the final revision of this work he was supported by funding from the European Research Council under the European Union's Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement no. 307119.

References

Alexeev, V., Boundedness and $K^{2}$ for log surfaces, Int. J. Math. 5 (1994), 779–810.CrossRefGoogle Scholar
Ambro, F., Shokurov's boundary property, J. Differential Geom. 67 (2004), 229–255.10.4310/jdg/1102536201CrossRefGoogle Scholar
Ambro, F., The moduli b-divisor of an lc-trivial fibration, Compos. Math. 141 (2005), 385–403.CrossRefGoogle Scholar
Batyrev, V., Stringy Hodge numbers of varieties with Gorenstein canonical singularities, in Integrable systems and algebraic geometry (World Scientific Publishing, Singapore, 1999), 1–32.Google Scholar
Beauville, A., Variétés Kähleriennes dont la première classe de Chern est nulle, J. Differential Geom. 18 (1983), 755–782.10.4310/jdg/1214438181CrossRefGoogle Scholar
Birkar, C., Singularities on the base of a Fano type fibration, J. Reine Angew. Math. 715 (2016), 125–142.Google Scholar
Birkar, C., Log Calabi–Yau fibrations, Preprint (2018), arXiv:1811.10709v2.Google Scholar
Birkar, C., Anti-pluricanonical systems on Fano varieties, Ann. of Math. (2) 190 (2019), 345–463.CrossRefGoogle Scholar
Birkar, C., Singularities of linear systems and boundedness of Fano varieties, Ann. of Math. (2) 193 (2021), 347–405Google Scholar
Birkar, C., Cascini, P., Hacon, C. and McKernan, J., Existence of minimal models for varieties of log general type, J. Amer. Math. Soc. 23 (2010), 405–468.CrossRefGoogle Scholar
Birkar, C., Di Cerbo, G. and Svaldi, R., Boundedness of elliptic Calabi–Yau varieties with a rational section, Preprint (2020), arXiv:2010.09769v1.Google Scholar
Birkar, C. and Zhang, D.-Q., Effectivity of Iitaka fibrations and pluricanonical systems of polarized pairs, Publ. Math. Inst. Hautes Études Sci. 123 (2016), 283.10.1007/s10240-016-0080-xCrossRefGoogle Scholar
Chen, W., Di Cerbo, G., Han, J., Jiang, C. and Svaldi, R., Birational boundedness of rationally connected Calabi–Yau 3-folds, Adv. Math. 378 (2021), 107541.CrossRefGoogle Scholar
Filipazzi, S., On a generalized canonical bundle formula and generalized adjunction, Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) XXI (2020), 1187–1221.Google Scholar
Filipazzi, S., Some remarks on the volume of log varieties, Proc. Edinb. Math. Soc. (2) 63 (2020), 314–322.10.1017/S0013091519000397CrossRefGoogle Scholar
Filipazzi, S., On the boundedness of $n$-folds with $\kappa (X)=n-1$, Preprint (2020), arXiv:2005.05508v2.Google Scholar
Filipazzi, S. and Svaldi, R., Invariance of plurigenera and boundedness for generalized pairs, Mat. Contemp. 47 (2020), 114–150.Google Scholar
Floris, E., Inductive approach to effective b-semiampleness, Int. Math. Res. Not. IMRN 2014 (2014), 1465–1492.CrossRefGoogle Scholar
Fujino, O., On Kawamata's theorem, in Classification of algebraic varieties, EMS Series of Congress Reports (European Mathematical Society, Zurich, 2011), 305–315.CrossRefGoogle Scholar
Fujino, O., Non-vanishing theorem for log canonical pairs, J. Algebraic Geom. 20 (2011), 771–783.10.1090/S1056-3911-2010-00558-9CrossRefGoogle Scholar
Fujino, O. and Gongyo, Y., On canonical bundle formulas and subadjunctions, Michigan Math. J. 61 (2012), 255–264. doi:10.1307/mmj/1339011526.CrossRefGoogle Scholar
Gongyo, Y. and Lehmann, B., Reduction maps and minimal model theory, Compos. Math. 149 (2013), 295–308.10.1112/S0010437X12000553CrossRefGoogle Scholar
Gross, M., A finiteness theorem for elliptic Calabi-Yau threefolds, Duke Math. J. 74 (1994), 271–299.CrossRefGoogle Scholar
Hacon, C., McKernan, J. and Xu, C., On the birational automorphisms of varieties of general type, Ann. of Math. (2) 177 (2013), 1077–1111.CrossRefGoogle Scholar
Hacon, C., McKernan, J. and Xu, C., ACC for log canonical thresholds, Ann. of Math. (2) 180 (2014), 523–571.CrossRefGoogle Scholar
Hacon, C., McKernan, J. and Xu, C., Boundedness of moduli of varieties of general type, J. Eur. Math. Soc. (JEMS) 20 (2018), 865–901.CrossRefGoogle Scholar
Hacon, C. and Xu, C., Existence of log canonical closures, Invent. Math. 192 (2013), 161–195.10.1007/s00222-012-0409-0CrossRefGoogle Scholar
Hacon, C. and Xu, C., Boundedness of log Calabi-Yau pairs of Fano type, Math. Res. Lett. 22 (2015), 1699–1716.CrossRefGoogle Scholar
Han, J. and Liu, W., On a generalized canonical bundle formula for generically finite morphisms, Ann. Inst. Fourier (Grenoble), to appear. Preprint (2019), arXiv:1905.12542v3.Google Scholar
Hartshorne, R., Algebraic geometry, Graduate Texts In Mathematics, vol. 52 (Springer, New York, 1977).10.1007/978-1-4757-3849-0CrossRefGoogle Scholar
Jiang, C., On birational boundedness of Fano fibrations, Amer. J. Math. 140 (2018), 1253–1276.10.1353/ajm.2018.0030CrossRefGoogle Scholar
Kollár, J., Effective base point freeness, Math. Ann. 296 (1993), 595–605.CrossRefGoogle Scholar
Kollár, J., Rational curves on algebraic varieties, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge/A Series of Modern Surveys in Mathematics, vol. 32 (Springer, Berlin, 1996).CrossRefGoogle Scholar
Kollár, J., Singularities of pairs, algebraic geometry—Santa Cruz 1995, Proc. Sympos. Pure Math. 62 (1997), 221–287.CrossRefGoogle Scholar
Kollár, J., Singularities of the minimal model program, with the collaboration of Sándor Kovács, Cambridge Tracts in Mathematics, vol. 200 (Cambridge University Press, Cambridge, 2013).CrossRefGoogle Scholar
Kollár, J. and Larsen, M., Quotients of Calabi-Yau varieties. Algebra, Arithmetic, and Geometry: In Honor of Yu. I. Manin. Vol. II, Progress in Mathematics, vol. 270 (Birkhäuser, Boston, MA, 2009), 179–211.Google Scholar
Kollár, J. and Mori, S., Birational geometry of algebraic varieties, Cambridge Tracts in Mathematics, vol. 134 (Cambridge University Press, 1998).CrossRefGoogle Scholar
Lai, C.-J., Varieties fibered by good minimal models, Math. Ann. 350 (2011), 533–547.10.1007/s00208-010-0574-7CrossRefGoogle Scholar
Lazarsfeld, R., Positivity in algebraic geometry I, II, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge/A Series of Modern Surveys in Mathematics, vol. 48 (Springer, Berlin, 2004).10.1007/978-3-642-18810-7CrossRefGoogle Scholar
Martinelli, D., Schreieder, S. and Tasin, L., On the number and boundedness of log minimal models of general type, Ann. Sci. Éc. Norm. Supér. (4) 53 (2020), 1183–1210.CrossRefGoogle Scholar
McKernan, J. and Prokhorov, Y., Threefold thresholds, Manuscripta Math. 114 (2004), 281–304.CrossRefGoogle Scholar
Oguiso, K. and Truong, T. T., Explicit examples of rational and Calabi-Yau threefolds with primitive automorphisms of positive entropy, J. Math. Sci. Univ. Tokyo 22 (2015), 361–385.Google Scholar
Prokhorov, Y. and Shokurov, V., Towards the second main theorem on complements, J. Algebraic Geom. 18 (2009), 151–199.CrossRefGoogle Scholar
Taylor, W. and Wang, Y.-N., The F-theory geometry with most flux vacua, J. High Energy Phys. 2015 (2015), 1–21.10.1007/JHEP12(2015)164CrossRefGoogle Scholar
Verdier, J.-L., Stratifications de Whitney et théorème de Bertini-Sard, Invent. Math. 36 (1976), 295–312.CrossRefGoogle Scholar
Veys, W., $\zeta$ functions and “Kontsevich invariants” on singular varieties, Canad. J. Math. 53 (2001), 834–865.CrossRefGoogle Scholar