Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-22T13:24:13.990Z Has data issue: false hasContentIssue false
  • English
  • Français

Arc-smooth functions on closed sets

Part of: Real functions: Miscellaneous topics Functions of several variables Calculus on manifolds; nonlinear operators

Published online by Cambridge University Press:  15 March 2019

Armin Rainer
Armin Rainer*
Affiliation:
University of Education Lower Austria, Campus Baden Mühlgasse 67, A-2500 Baden, Austria email armin.rainer@univie.ac.at Fakultät für Mathematik, Universität Wien, Oskar-Morgenstern-Platz 1, A-1090 Wien, Austria
Get access Rights & Permissions [Opens in a new window]

Abstract

By an influential theorem of Boman, a function 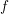$f$ on an open set 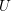$U$ in 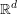$\mathbb{R}^{d}$ is smooth (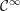${\mathcal{C}}^{\infty }$) if and only if it is arc-smooth, that is, 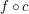$f\,\circ \,c$ is smooth for every smooth curve 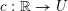$c:\mathbb{R}\rightarrow U$. In this paper we investigate the validity of this result on closed sets. Our main focus is on sets which are the closure of their interior, so-called fat sets. We obtain an analogue of Boman’s theorem on fat closed sets with Hölder boundary and on fat closed subanalytic sets with the property that every boundary point has a basis of neighborhoods each of which intersects the interior in a connected set. If 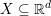$X\subseteq \mathbb{R}^{d}$ is any such set and 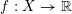$f:X\rightarrow \mathbb{R}$ is arc-smooth, then 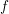$f$ extends to a smooth function defined on 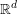$\mathbb{R}^{d}$. We also get a version of the Bochnak–Siciak theorem on all closed fat subanalytic sets and all closed sets with Hölder boundary: if 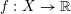$f:X\rightarrow \mathbb{R}$ is the restriction of a smooth function on 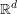$\mathbb{R}^{d}$ which is real analytic along all real analytic curves in 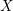$X$, then 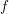$f$ extends to a holomorphic function on a neighborhood of 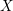$X$ in 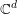$\mathbb{C}^{d}$. Similar results hold for non-quasianalytic Denjoy–Carleman classes (of Roumieu type). We will also discuss sharpness and applications of these results.

Keywords

differentiability on closed setsultradifferentiable functionsBoman’s theoremBochnak–Siciak theoremFrölicher spacessubanalytic sets

MSC classification

Primary: 26B05: Continuity and differentiation questions 26B35: Special properties of functions of several variables, Hölder conditions, etc. 26E10: $C^infty$-functions, quasi-analytic functions 32B20: Semi-analytic sets and subanalytic sets 58C25: Differentiable maps
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 4 , April 2019 , pp. 645 - 680
Copyright
© The Author 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Supported by FWF-Project P 26735-N25.

References

Alekseevsky, D., Kriegl, A., Losik, M. and Michor, P. W., Lifting smooth curves over invariants for representations of compact Lie groups , Transform. Groups 5 (2000), 103–110.Google Scholar
Amemiya, I. and Masuda, K., On Joris’ theorem on differentiability of functions , Kodai Math. J. 12 (1989), 92–97.10.2996/kmj/1138038992Google Scholar
Belotto da Silva, A., Bierstone, E. and Chow, M., Composite quasianalytic functions , Compos. Math. 154 (2018), 1960–1973.10.1112/S0010437X18007339Google Scholar
Bierstone, E., Differentiable functions , Bol. Soc. Brasil. Mat. 11 (1980), 139–189.10.1007/BF02584636Google Scholar
Bierstone, E. and Milman, P. D., Composite differentiable functions , Ann. of Math. (2) 116 (1982), 541–558.Google Scholar
Bierstone, E. and Milman, P. D., Semianalytic and subanalytic sets , Publ. Math. Inst. Hautes Études Sci. 67 (1988), 5–42.10.1007/BF02699126Google Scholar
Bierstone, E. and Milman, P. D., Geometric and differential properties of subanalytic sets , Ann. of Math. (2) 147 (1998), 731–785.Google Scholar
Bierstone, E., Milman, P. D. and Parusiński, A., A function which is arc-analytic but not continuous , Proc. Amer. Math. Soc. 113 (1991), 419–423.Google Scholar
Bierstone, E., Milman, P. D. and Pawłucki, W., Composite differentiable functions , Duke Math. J. 83 (1996), 607–620.10.1215/S0012-7094-96-08318-0Google Scholar
Bochnak, J., Analytic functions in Banach spaces , Studia Math. 35 (1970), 273–292.Google Scholar
Boman, J., Differentiability of a function and of its compositions with functions of one variable , Math. Scand. 20 (1967), 249–268.10.7146/math.scand.a-10835Google Scholar
Bruna, J., An extension theorem of Whitney type for non-quasi-analytic classes of functions , J. Lond. Math. Soc. (2) 22 (1980), 495–505.10.1112/jlms/s2-22.3.495Google Scholar
Bochnak, J. and Siciak, J., Analytic functions in topological vector spaces , Studia Math. 39 (1971), 77–112.Google Scholar
Chaumat, J. and Chollet, A.-M., Propriétés de l’intersection des classes de Gevrey et de certaines autres classes , Bull. Sci. Math. 122 (1998), 455–485.10.1016/S0007-4497(98)80003-1Google Scholar
Chaumat, J. and Chollet, A.-M., Sur la division et la composition dans des classes ultradifférentiables , Studia Math. 136 (1999), 49–70 (French).Google Scholar
Duncan, J., Krantz, S. G. and Parks, H. R., Nonlinear conditions for differentiability of functions , J. Anal. Math. 45 (1985), 46–68.10.1007/BF02792545Google Scholar
Delfour, M. C. and Zolésio, J.-P., Shapes and geometries. Metrics, analysis, differential calculus, and optimization, second edition (Society for Industrial and Applied Mathematics, Philadelphia, PA, 2011).Google Scholar
Eakin, P. M. and Harris, G. A., When F (f) convergent implies f is convergent , Math. Ann. 229 (1977), 201–210.Google Scholar
Faure, C.-A. and Frölicher, A., Hölder differentiable maps and their function spaces , in Categorical topology and its relation to analysis, algebra and combinatorics (Prague, 1988) (World Scientific, Teaneck, NJ, 1989), 135–142.Google Scholar
Frölicher, A. and Kriegl, A., Linear spaces and differentiation theory , in Pure and applied mathematics (New York) (John Wiley & Sons, Chichester, 1988).Google Scholar
Gabriélov, A. M., Formal relations among analytic functions , Izv. Akad. Nauk SSSR Ser. Mat. 37 (1973), 1056–1090.Google Scholar
Glaeser, G., Racine carrée d’une fonction différentiable , Ann. Inst. Fourier (Grenoble) 13 (1963), 203–210.Google Scholar
Grisvard, P., Elliptic problems in nonsmooth domains, Monographs and Studies in Mathematics, vol. 24 (Pitman, Boston, 1985).Google Scholar
Hardt, R. M., Some analytic bounds for subanalytic sets , in Differential geometric control theory (Houghton, Mich., 1982), Progress in Mathematics, vol. 27 (Birkhäuser, Boston, 1983), 259–267.Google Scholar
Hironaka, H., Introduction to real-analytic sets and real-analytic maps, Quaderni dei Gruppi di Ricerca Matematica del Consiglio Nazionale delle Ricerche. Istituto Matematico ‘L. Tonelli’ dell’Università di Pisa, Pisa, 1973.Google Scholar
Jaffe, E. Y., Pathological phenomena in Denjoy–Carleman classes , Canad. J. Math. 68 (2016), 88–108.Google Scholar
Joris, H., Une C ∞ -application non-immersive qui possède la propriété universelle des immersions , Arch. Math. (Basel) 39 (1982), 269–277.10.1007/BF01899535Google Scholar
Joris, H. and Preissmann, E., Pseudo-immersions , Ann. Inst. Fourier (Grenoble) 37 (1987), 195–221.Google Scholar
Joris, H. and Preissmann, E., Quotients of smooth functions , Kodai Math. J. 13 (1990), 241–264.Google Scholar
Kriegl, A. and Michor, P. W., The convenient setting of global analysis, Mathematical Surveys and Monographs, vol. 53 (American Mathematical Society, Providence, RI, 1997); http://www.ams.org/online_bks/surv53/.Google Scholar
Kriegl, A., Michor, P. W. and Rainer, A., The convenient setting for non-quasianalytic Denjoy–Carleman differentiable mappings , J. Funct. Anal. 256 (2009), 3510–3544.Google Scholar
Kriegl, A., Michor, P. W. and Rainer, A., The convenient setting for quasianalytic Denjoy–Carleman differentiable mappings , J. Funct. Anal. 261 (2011), 1799–1834.10.1016/j.jfa.2011.05.019Google Scholar
Komatsu, H., An analogue of the Cauchy–Kowalevsky theorem for ultradifferentiable functions and a division theorem for ultradistributions as its dual , J. Fac. Sci. Univ. Tokyo Sect. IA Math. 26 (1979), 239–254.Google Scholar
Kurdyka, K. and Parusiński, A., Quasi-convex decomposition in o-minimal structures. Application to the gradient conjecture , in Singularity theory and its applications, Advanced Studies in Pure Mathematics, vol. 43 (Mathematical Society of Japan, Tokyo, 2006), 137–177.Google Scholar
Kriegl, A., Remarks on germs in infinite dimensions , Acta Math. Univ. Comenian. (N.S.) 66 (1997), 117–134.Google Scholar
Kurdyka, K., On a subanalytic stratification satisfying a Whitney property with exponent 1 , in Real algebraic geometry (Rennes, 1991), Lecture Notes in Mathematics, vol. 1524 (Springer, Berlin, 1992), 316–322.10.1007/BFb0084630Google Scholar
Luna, D., Fonctions différentiables invariantes sous l’opération d’un groupe réductif , Ann. Inst. Fourier (Grenoble) 26 (1976), 33–49.10.5802/aif.599Google Scholar
Malgrange, B., Ideals of differentiable functions, Tata Institute of Fundamental Research Studies in Mathematics, vol. 3 (Tata Institute of Fundamental Research, Bombay, 1967).Google Scholar
Mather, J. N., Differentiable invariants , Topology 16 (1977), 145–155.10.1016/0040-9383(77)90012-XGoogle Scholar
Neelon, T., Ultradifferentiable functions on lines in ℝ n , Proc. Amer. Math. Soc. 127 (1999), 2099–2104.10.1090/S0002-9939-99-04759-0Google Scholar
Parusiński, A., Lipschitz stratification of subanalytic sets , Ann. Sc. Éc. Norm. Supér. (4) 27 (1994), 661–696.Google Scholar
Parusiński, A., Subanalytic functions , Trans. Amer. Math. Soc. 344 (1994), 583–595.Google Scholar
Pawłucki, W., Lipschitz cell decomposition in o-minimal structures. I , Illinois J. Math. 52 (2008), 1045–1063.Google Scholar
Pawłucki, W. and Pleśniak, W., Markov’s inequality and C ∞ functions on sets with polynomial cusps , Math. Ann. 275 (1986), 467–480.10.1007/BF01458617Google Scholar
Pawłucki, W. and Pleśniak, W., Extension of C ∞ functions from sets with polynomial cusps , Studia Math. 88 (1988), 279–287.10.4064/sm-88-3-279-287Google Scholar
Parusiński, A. and Rainer, A., Lifting differentiable curves from orbit spaces , Transform. Groups 21 (2016), 153–179.Google Scholar
Procesi, C. and Schwarz, G., Inequalities defining orbit spaces , Invent. Math. 81 (1985), 539–554.Google Scholar
Rainer, A., Recognizing (ultra)differentiable functions on closed sets , Oberwolfach Report 14 (2017), 1369–1372.Google Scholar
Rahman, Q. I. and Schmeisser, G., Analytic theory of polynomials, London Mathematical Society Monographs, New Series, vol. 26 (Clarendon Press, Oxford, 2002).Google Scholar
Rainer, A. and Schindl, G., Composition in ultradifferentiable classes , Studia Math. 224 (2014), 97–131.Google Scholar
Rainer, A. and Schindl, G., Equivalence of stability properties for ultradifferentiable function classes , Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. RACSAM. 110 (2016), 17–32.Google Scholar
Schwarz, G. W., Smooth functions invariant under the action of a compact Lie group , Topology 14 (1975), 63–68.Google Scholar
Siciak, J., A characterization of analytic functions of n real variables , Studia Math. 35 (1970), 293–297.Google Scholar