Article contents
An exceptional Siegel–Weil formula and poles of the Spin L-function of 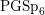 $\text{PGSp}_{6}$
$\text{PGSp}_{6}$
Published online by Cambridge University Press: 29 May 2020
Abstract
We show a Siegel–Weil formula in the setting of exceptional theta correspondence. Using this, together with a new Rankin–Selberg integral for the Spin L-function of 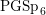 $\text{PGSp}_{6}$ discovered by Pollack, we prove that a cuspidal representation of
$\text{PGSp}_{6}$ discovered by Pollack, we prove that a cuspidal representation of 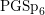 $\text{PGSp}_{6}$ is a (weak) functorial lift from the exceptional group
$\text{PGSp}_{6}$ is a (weak) functorial lift from the exceptional group 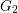 $G_{2}$ if its (partial) Spin L-function has a pole at
$G_{2}$ if its (partial) Spin L-function has a pole at 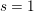 $s=1$.
$s=1$.
- Type
- Research Article
- Information
- Copyright
- © The Authors 2020
References
- 1
- Cited by


