Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Shen, Zhijun
Yan, Wei
and
Yuan, Guangwei
2014.
A Stability Analysis of Hybrid Schemes to Cure Shock Instability.
Communications in Computational Physics,
Vol. 15,
Issue. 5,
p.
1320.
Powers, Joseph M.
Bruns, Jeffrey D.
and
Jemcov, Aleksandar
2015.
Physical Diffusion Cures the Carbuncle Phenomenon.
Winters, Andrew R.
and
Gassner, Gregor J.
2016.
Affordable, entropy conserving and entropy stable flux functions for the ideal MHD equations.
Journal of Computational Physics,
Vol. 304,
Issue. ,
p.
72.
Cheng, Xiaohan
and
Nie, Yufeng
2016.
A third-order entropy stable scheme for hyperbolic conservation laws.
Journal of Hyperbolic Differential Equations,
Vol. 13,
Issue. 01,
p.
129.
Gassner, Gregor J.
Winters, Andrew R.
and
Kopriva, David A.
2016.
Split form nodal discontinuous Galerkin schemes with summation-by-parts property for the compressible Euler equations.
Journal of Computational Physics,
Vol. 327,
Issue. ,
p.
39.
Chandrashekar, Praveen
and
Klingenberg, Christian
2016.
Entropy Stable Finite Volume Scheme for Ideal Compressible MHD on 2-D Cartesian Meshes.
SIAM Journal on Numerical Analysis,
Vol. 54,
Issue. 2,
p.
1313.
Ray, Deep
Chandrashekar, Praveen
Fjordholm, Ulrik S.
and
Mishra, Siddhartha
2016.
Entropy Stable Scheme on Two-Dimensional Unstructured Grids for Euler Equations.
Communications in Computational Physics,
Vol. 19,
Issue. 5,
p.
1111.
Derigs, Dominik
Winters, Andrew R.
Gassner, Gregor J.
and
Walch, Stefanie
2017.
A novel averaging technique for discrete entropy-stable dissipation operators for ideal MHD.
Journal of Computational Physics,
Vol. 330,
Issue. ,
p.
624.
Ray, Deep
and
Chandrashekar, Praveen
2017.
An entropy stable finite volume scheme for the two dimensional Navier–Stokes equations on triangular grids.
Applied Mathematics and Computation,
Vol. 314,
Issue. ,
p.
257.
Ortleb, Sigrun
2017.
A Kinetic Energy Preserving DG Scheme Based on Gauss–Legendre Points.
Journal of Scientific Computing,
Vol. 71,
Issue. 3,
p.
1135.
Chen, Tianheng
and
Shu, Chi-Wang
2017.
Entropy stable high order discontinuous Galerkin methods with suitable quadrature rules for hyperbolic conservation laws.
Journal of Computational Physics,
Vol. 345,
Issue. ,
p.
427.
Crean, Jared
Hicken, Jason E.
Del Rey Fernández, David C.
Zingg, David W.
and
Carpenter, Mark
2017.
High-Order, Entropy-Conservative Discretizations of the Euler Equations for Complex Geometries.
Winters, Andrew R.
Derigs, Dominik
Gassner, Gregor J.
and
Walch, Stefanie
2017.
A uniquely defined entropy stable matrix dissipation operator for high Mach number ideal MHD and compressible Euler simulations.
Journal of Computational Physics,
Vol. 332,
Issue. ,
p.
274.
Balsara, Dinshaw S.
2017.
Higher-order accurate space-time schemes for computational astrophysics—Part I: finite volume methods.
Living Reviews in Computational Astrophysics,
Vol. 3,
Issue. 1,
Schmidtmann, Birte
and
Winters, Andrew R.
2017.
Hybrid entropy stable HLL-type Riemann solvers for hyperbolic conservation laws.
Journal of Computational Physics,
Vol. 330,
Issue. ,
p.
566.
Ranocha, Hendrik
2018.
Comparison of Some Entropy Conservative Numerical Fluxes for the Euler Equations.
Journal of Scientific Computing,
Vol. 76,
Issue. 1,
p.
216.
Lozano, Carlos
2018.
Entropy Production by Explicit Runge–Kutta Schemes.
Journal of Scientific Computing,
Vol. 76,
Issue. 1,
p.
521.
Chan, Jesse
2018.
On discretely entropy conservative and entropy stable discontinuous Galerkin methods.
Journal of Computational Physics,
Vol. 362,
Issue. ,
p.
346.
Kuya, Yuichi
Totani, Kosuke
and
Kawai, Soshi
2018.
Kinetic energy and entropy preserving schemes for compressible flows by split convective forms.
Journal of Computational Physics,
Vol. 375,
Issue. ,
p.
823.
Biswas, Biswarup
and
Dubey, Ritesh Kumar
2018.
Low dissipative entropy stable schemes using third order WENO and TVD reconstructions.
Advances in Computational Mathematics,
Vol. 44,
Issue. 4,
p.
1153.
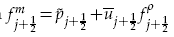 where
where 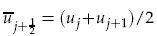 and
and 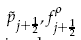 are any consistent approximations to the pressure and the mass flux. This scheme thus leaves most terms in the numerical flux unspecified and various authors have used simple averaging. Here we enforce approximate or exact entropy consistency which leads to a unique choice of all the terms in the numerical fluxes. As a consequence novel entropy conservative flux that also preserves kinetic energy for the semi-discrete finite volume scheme has been proposed. These fluxes are centered and some dissipation has to be added if shocks are present or if the mesh is coarse. We construct scalar artificial dissipation terms which are kinetic energy stable and satisfy approximate/exact entropy condition. Secondly, we use entropy-variable based matrix dissipation flux which leads to kinetic energy and entropy stable schemes. These schemes are shown to be free of entropy violating solutions unlike the original Roe scheme. For hypersonic flows a blended scheme is proposed which gives carbuncle free solutions for blunt body flows. Numerical results for Euler and Navier-Stokes equations are presented to demonstrate the performance of the different schemes.
are any consistent approximations to the pressure and the mass flux. This scheme thus leaves most terms in the numerical flux unspecified and various authors have used simple averaging. Here we enforce approximate or exact entropy consistency which leads to a unique choice of all the terms in the numerical fluxes. As a consequence novel entropy conservative flux that also preserves kinetic energy for the semi-discrete finite volume scheme has been proposed. These fluxes are centered and some dissipation has to be added if shocks are present or if the mesh is coarse. We construct scalar artificial dissipation terms which are kinetic energy stable and satisfy approximate/exact entropy condition. Secondly, we use entropy-variable based matrix dissipation flux which leads to kinetic energy and entropy stable schemes. These schemes are shown to be free of entropy violating solutions unlike the original Roe scheme. For hypersonic flows a blended scheme is proposed which gives carbuncle free solutions for blunt body flows. Numerical results for Euler and Navier-Stokes equations are presented to demonstrate the performance of the different schemes.



