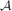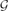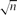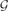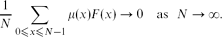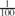A function f:  2n → {0,1} is odd-cycle-free if there are no x1,. . .,xk ∈
2n → {0,1} is odd-cycle-free if there are no x1,. . .,xk ∈  2n with k an odd integer such that f(x1) = ··· = f(xk) = 1 and x1 + ··· + xk = 0. We show that one can distinguish odd-cycle-free functions from those ε-far from being odd-cycle-free by making poly(1/ε) queries to an evaluation oracle. We give two proofs of this result, each shedding light on a different connection between testability of properties of Boolean functions and of dense graphs.
2n with k an odd integer such that f(x1) = ··· = f(xk) = 1 and x1 + ··· + xk = 0. We show that one can distinguish odd-cycle-free functions from those ε-far from being odd-cycle-free by making poly(1/ε) queries to an evaluation oracle. We give two proofs of this result, each shedding light on a different connection between testability of properties of Boolean functions and of dense graphs.
The first issue we study is directly reducing testing of linear-invariant properties of Boolean functions to testing associated graph properties. We show a black-box reduction from testing odd-cycle-freeness to testing bipartiteness of graphs. Such reductions have already been shown (Král’, Serra and Vena, and Shapira) for monotone linear-invariant properties defined by forbidding solutions to a finite number of equations. But for odd-cycle-freeness whose description involves an infinite number of forbidden equations, a reduction to graph property testing was not previously known. If one could show such a reduction more generally for any linear-invariant property closed under restrictions to subspaces, then it would likely lead to a characterization of the one-sided testable linear-invariant properties, an open problem raised by Sudan.
The second issue we study is whether there is an efficient canonical tester for linear-invariant properties of Boolean functions. A canonical tester for linear-invariant properties operates by picking a random linear subspace and then checking whether the restriction of the input function to the subspace satisfies a fixed property. The question is if, for every linear-invariant property, there is a canonical tester for which there is only a polynomial blow-up from the optimal query complexity. We answer the question affirmatively for odd-cycle-freeness. The general question remains open.