No CrossRef data available.
Article contents
Ramsey upper density of infinite graphs
Published online by Cambridge University Press: 25 April 2023
Abstract
For a fixed infinite graph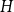 
$H$, we study the largest density of a monochromatic subgraph isomorphic to 
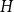$H$ that can be found in every two-colouring of the edges of 
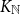$K_{\mathbb{N}}$. This is called the Ramsey upper density of 
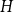$H$ and was introduced by Erdős and Galvin in a restricted setting, and by DeBiasio and McKenney in general. Recently [4], the Ramsey upper density of the infinite path was determined. Here, we find the value of this density for all locally finite graphs 
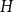$H$ up to a factor of 2, answering a question of DeBiasio and McKenney. We also find the exact density for a wide class of bipartite graphs, including all locally finite forests. Our approach relates this problem to the solution of an optimisation problem for continuous functions. We show that, under certain conditions, the density depends only on the chromatic number of 
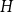$H$, the number of components of 
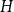$H$ and the expansion ratio 
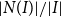$|N(I)|/|I|$ of the independent sets of 
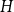$H$.
MSC classification
Primary:
05C55: Generalized Ramsey theory
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
Footnotes
*
Funded from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 648509). This publication reflects only its author’s view; the European Research Council Executive Agency is not responsible for any use that may be made of the information it contains. Also supported by the MUNI Award in Science and Humanities of the Grant Agency of Masaryk University.
†
Former affiliation: Freie Universität Berlin
References
Balogh, J. and Lamaison, A. (2020) Ramsey upper density of infinite graph factors. https://arxiv.org/abs/2010.13633
Google Scholar
Burke, J. R. and Webb, W. A. (1981) Asymptotic behavior of linear recurrences. Fibonacci Quart. 19(4) 318–321.Google Scholar
Burr, S. A., Erdős, P. and Spencer, J. H. (1975) Ramsey theorems for multiple copies of graphs. Trans. Amer. Math. Soc. 209 87–99.CrossRefGoogle Scholar
Corsten, J., DeBiasio, L., Lamaison, A. and Lang, R. (2019) Upper density of monochromatic infinite paths. Adv. Comb 4 16.Google Scholar
Corsten, J., DeBiasio, L. and McKenney, P. (2020) Density of monochromatic infinite subgraphs ii. https://arxiv.org/abs/2007.14277
Google Scholar
DeBiasio, L. and McKenney, P. (2019) Density of monochromatic infinite subgraphs. Combinatorica 39(4) 847–878.CrossRefGoogle Scholar
Elekes, M., Soukup, D. T., Soukup, L. and Szentmiklóssy, Z. (2017) Decompositions of edge-colored infinite complete graphs into monochromatic paths. Discrete Math. 340(8) 2053–2069.CrossRefGoogle Scholar
Erdős, P. and Galvin, F. (1993) Monochromatic infinite paths. Discrete Math. 113(1-3) 59–70.CrossRefGoogle Scholar
Komlós, J. and Simonovits, M. (1996) Szemerédi’s Regularity Lemma and its applications in graph theory, Combinatorics, Paul Erdős is Eighty, Vol. 2, Miklós, D., Sós, V. T. and Szőnyi, T., Bolyai Society Mathematical Studies, pp. 295–352.Google Scholar
Lo, A., Sanhueza-Matamala, N. and Wang, G. (2018) Density of monochromatic infinite paths. Electron. J. Combin. 25(4) #P4.29.CrossRefGoogle Scholar