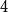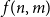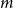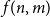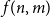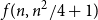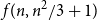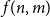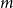1. Introduction
One of the central questions in extremal combinatorics can be formulated as follows. Given a graph
![]() $G$
and a property
$G$
and a property
![]() $\mathcal{P}$
, what is the maximal subgraph of
$\mathcal{P}$
, what is the maximal subgraph of
![]() $G$
one can find which satisfies this property. The study of this problem goes back to the work of Turán in 1941, whose theorem states that the largest subgraph of the
$G$
one can find which satisfies this property. The study of this problem goes back to the work of Turán in 1941, whose theorem states that the largest subgraph of the
![]() $n$
-vertex complete graph with no clique of size
$n$
-vertex complete graph with no clique of size
![]() $k+1$
is the complete
$k+1$
is the complete
![]() $k$
-partite graph with sides as equal as possible. This graph is called the Turán graph. We denote it by
$k$
-partite graph with sides as equal as possible. This graph is called the Turán graph. We denote it by
![]() $T_k(n)$
and its size by
$T_k(n)$
and its size by
![]() $t_k(n)$
. Turán’s theorem is the starting point of extremal graph theory and has inspired extensive research. One such research direction studies which other (more elaborate) structures must appear in a graph with more than
$t_k(n)$
. Turán’s theorem is the starting point of extremal graph theory and has inspired extensive research. One such research direction studies which other (more elaborate) structures must appear in a graph with more than
![]() $t_k(n)$
edges. For example, a series of works determined how many
$t_k(n)$
edges. For example, a series of works determined how many
![]() $(k+1)$
-cliques must exist in a graph with
$(k+1)$
-cliques must exist in a graph with
![]() $t_k(n) + a$
edges (for a suitable range of
$t_k(n) + a$
edges (for a suitable range of
![]() $a$
) [Reference Erdős7, Reference Erdős11, Reference Lovász and Simonovits16]. Other examples are results on finding many
$a$
) [Reference Erdős7, Reference Erdős11, Reference Lovász and Simonovits16]. Other examples are results on finding many
![]() $(k+1)$
-cliques which share one or more vertices [Reference Edwards5, Reference Erdős7, Reference Erdős, Furedi, Gould and Gunderson8, Reference Khadžiivanov and Nikiforov15], and results on finding
$(k+1)$
-cliques which share one or more vertices [Reference Edwards5, Reference Erdős7, Reference Erdős, Furedi, Gould and Gunderson8, Reference Khadžiivanov and Nikiforov15], and results on finding
![]() $(k+1)$
-cliques with large degree sum [Reference Bollobás and Nikiforov1, Reference Edwards3, Reference Edwards4, Reference Faudree12].
$(k+1)$
-cliques with large degree sum [Reference Bollobás and Nikiforov1, Reference Edwards3, Reference Edwards4, Reference Faudree12].
In this paper we study the Turán type problem for chordal graphs. A graph is called chordal if it contains no induced cycle of length at least
![]() $4$
. Chordal graphs are one of the most studied classes in graph theory and have numerous applications, for example in semidefinite optimisation (see the survey [Reference Vandenberghe and Andersen17]) and evolutionary trees (see [Reference Enright and Kondrak6]). In 1985, Erdős and Laskar [Reference Erdős and Laskar10] asked to determine the maximum integer
$4$
. Chordal graphs are one of the most studied classes in graph theory and have numerous applications, for example in semidefinite optimisation (see the survey [Reference Vandenberghe and Andersen17]) and evolutionary trees (see [Reference Enright and Kondrak6]). In 1985, Erdős and Laskar [Reference Erdős and Laskar10] asked to determine the maximum integer
![]() $f(n,m)$
such that every graph with
$f(n,m)$
such that every graph with
![]() $n$
vertices and
$n$
vertices and
![]() $m$
edges contains a chordal subgraph with at least
$m$
edges contains a chordal subgraph with at least
![]() $f(n,m)$
edges. To put this question under the umbrella of classical extremal graph theory, one needs to consider equivalent definitions of chordal graphs. It is well known that a graph is chordal if and only if it can be constructed from a single-vertex graph by repeatedly adding a vertex and connecting it to a clique of the current graphFootnote
1
(this is called a perfect elimination ordering), see [Reference Golumbic13, Chapter 4]. So if
$f(n,m)$
edges. To put this question under the umbrella of classical extremal graph theory, one needs to consider equivalent definitions of chordal graphs. It is well known that a graph is chordal if and only if it can be constructed from a single-vertex graph by repeatedly adding a vertex and connecting it to a clique of the current graphFootnote
1
(this is called a perfect elimination ordering), see [Reference Golumbic13, Chapter 4]. So if
![]() $G$
is a triangle-free graph, then every chordal subgraph of
$G$
is a triangle-free graph, then every chordal subgraph of
![]() $G$
must be a forest. More generally, if
$G$
must be a forest. More generally, if
![]() $G$
has no cliques of size
$G$
has no cliques of size
![]() $k+1$
, then every chordal subgraph of
$k+1$
, then every chordal subgraph of
![]() $G$
has at most
$G$
has at most
![]() $(k-1)(n-k+1) + \binom{k-1}{2} = (k-1)n - \binom{k}{2}$
edges. In particular, this bound applies to
$(k-1)(n-k+1) + \binom{k-1}{2} = (k-1)n - \binom{k}{2}$
edges. In particular, this bound applies to
![]() $k$
-partite graphs. Another way of proving this bound for
$k$
-partite graphs. Another way of proving this bound for
![]() $k$
-partite graphs is to observe that if
$k$
-partite graphs is to observe that if
![]() $G$
is
$G$
is
![]() $k$
-partite with parts
$k$
-partite with parts
![]() $V_1,\dots,V_k$
and
$V_1,\dots,V_k$
and
![]() $H$
is a chordal subgraph of
$H$
is a chordal subgraph of
![]() $G$
, then
$G$
, then
![]() $e_H(V_i,V_j) \leq |V_i| + |V_j| - 1$
for every
$e_H(V_i,V_j) \leq |V_i| + |V_j| - 1$
for every
![]() $i \lt j$
(because a chordal subgraph of a bipartite graph must be a forest). Hence,
$i \lt j$
(because a chordal subgraph of a bipartite graph must be a forest). Hence,
![]() $e(H) \leq \sum _{i \lt j}(|V_i| + |V_j| - 1) = (k-1)n - \binom{k}{2}$
.
$e(H) \leq \sum _{i \lt j}(|V_i| + |V_j| - 1) = (k-1)n - \binom{k}{2}$
.
The above discussion shows that if
![]() $m \leq t_k(n)$
then
$m \leq t_k(n)$
then
![]() $f(n,m) \leq (k-1)n - \binom{k}{2}$
. It is natural to guess that the value of
$f(n,m) \leq (k-1)n - \binom{k}{2}$
. It is natural to guess that the value of
![]() $f(n,m)$
“jumps” as
$f(n,m)$
“jumps” as
![]() $m$
increases from
$m$
increases from
![]() $t_k(n)$
to
$t_k(n)$
to
![]() $m = t_k(n) + 1$
, because at this point the graph must contain
$m = t_k(n) + 1$
, because at this point the graph must contain
![]() $(k+1)$
-cliques. Erdős and Laskar [Reference Erdős and Laskar10] proved that this is indeed the case for
$(k+1)$
-cliques. Erdős and Laskar [Reference Erdős and Laskar10] proved that this is indeed the case for
![]() $k=2$
, showing that
$k=2$
, showing that
![]() $f(n,t_2(n)+1) \geq (1+\varepsilon )n$
. In the late 80’s, Erdős, Gyárfás, Ordman and Zalcstein [Reference Erdős, Gyárfás, Ordman and Zalcstein9] determined the value of
$f(n,t_2(n)+1) \geq (1+\varepsilon )n$
. In the late 80’s, Erdős, Gyárfás, Ordman and Zalcstein [Reference Erdős, Gyárfás, Ordman and Zalcstein9] determined the value of
![]() $f(n,t_2(n)+1)$
exactly for even
$f(n,t_2(n)+1)$
exactly for even
![]() $n$
, showing that
$n$
, showing that
![]() $f\!\left(n,\frac{n^2}{4}+1\right) = \frac{3n}{2} - 1$
. This bound is achieved by the graph
$f\!\left(n,\frac{n^2}{4}+1\right) = \frac{3n}{2} - 1$
. This bound is achieved by the graph
![]() $T_2(n) + e$
, obtained by adding an edge to the Turán graph
$T_2(n) + e$
, obtained by adding an edge to the Turán graph
![]() $T_2(n)$
. It is natural to conjecture that for every
$T_2(n)$
. It is natural to conjecture that for every
![]() $k$
and
$k$
and
![]() $n$
, the value of
$n$
, the value of
![]() $f(n,t_k(n)+1)$
is determined by
$f(n,t_k(n)+1)$
is determined by
![]() $T_k(n) + e$
, which is the graph obtained by adding an edge to a largest class of
$T_k(n) + e$
, which is the graph obtained by adding an edge to a largest class of
![]() $T_k(n)$
. It is not hard to check that the largest chordal subgraph of
$T_k(n)$
. It is not hard to check that the largest chordal subgraph of
![]() $T_k(n)+e$
has
$T_k(n)+e$
has
![]() $kn - \lceil \frac{n}{k} \rceil + 2 - \binom{k+1}{2}$
edges. So we get the following conjecture.
$kn - \lceil \frac{n}{k} \rceil + 2 - \binom{k+1}{2}$
edges. So we get the following conjecture.
Conjecture 1.1.
![]() $f(n,t_k(n)+1) = kn - \lceil \frac{n}{k} \rceil + 2 - \binom{k+1}{2}$
.
$f(n,t_k(n)+1) = kn - \lceil \frac{n}{k} \rceil + 2 - \binom{k+1}{2}$
.
The authors of [Reference Erdős, Gyárfás, Ordman and Zalcstein9] only studied Conjecture 1.1 in the cases
![]() $k=2,3$
, although they very likely had the full conjecture in mind. For
$k=2,3$
, although they very likely had the full conjecture in mind. For
![]() $k=3$
, they proved that
$k=3$
, they proved that
![]() $f(n,t_3(n)+1) \geq 7n/3-6$
and asked to determine
$f(n,t_3(n)+1) \geq 7n/3-6$
and asked to determine
![]() $f(n,t_3(n)+1)$
. This question was later mentioned again in the problem survey of Gyárfás [Reference Gyárfás14]. Answering this question, we resolve Conjecture 1.1 for the case
$f(n,t_3(n)+1)$
. This question was later mentioned again in the problem survey of Gyárfás [Reference Gyárfás14]. Answering this question, we resolve Conjecture 1.1 for the case
![]() $k=3$
.
$k=3$
.
Theorem 1.2.
![]() $f(n,t_3(n)+1) = 3n-\lceil \frac{n}{3} \rceil - 4$
.
$f(n,t_3(n)+1) = 3n-\lceil \frac{n}{3} \rceil - 4$
.
Our next result proves Conjecture 1.1 asymptotically for every
![]() $k$
. In fact, we go a step further and determine
$k$
. In fact, we go a step further and determine
![]() $f(n,m)$
asymptotically for every value of
$f(n,m)$
asymptotically for every value of
![]() $m$
, answering the question of Erdős and Laskar.
$m$
, answering the question of Erdős and Laskar.
Theorem 1.3.
Let
![]() $k,n \geq 1$
and
$k,n \geq 1$
and
![]() $t_{k}(n)+1 \leq m \leq t_{k+1}(n)$
. Set
$t_{k}(n)+1 \leq m \leq t_{k+1}(n)$
. Set
![]() $a = m - t_k(n)$
. Then
$a = m - t_k(n)$
. Then
The construction giving the upper bound in Theorem 1.3 is to take an (unbalanced) complete
![]() $k$
-partite graph with
$k$
-partite graph with
![]() $k-1$
smaller classes of the same size and one bigger class, and to add a balanced complete bipartite graph inside the bigger class. One then needs to optimise the sizes of the classes and the size of the complete bipartite graph so as to minimise the size of chordal subgraphs. It is best to take the
$k-1$
smaller classes of the same size and one bigger class, and to add a balanced complete bipartite graph inside the bigger class. One then needs to optimise the sizes of the classes and the size of the complete bipartite graph so as to minimise the size of chordal subgraphs. It is best to take the
![]() $k-1$
smaller classes of size
$k-1$
smaller classes of size
![]() $\frac{n-r}{k}$
, the bigger class of size
$\frac{n-r}{k}$
, the bigger class of size
![]() $\frac{n+(k-1)r}{k}$
and the complete bipartite of size
$\frac{n+(k-1)r}{k}$
and the complete bipartite of size
![]() $r \times r$
, where
$r \times r$
, where
![]() $r \;:\!=\; \sqrt{\frac{2ka}{k+1}}$
. See Figure 1, and see Section 2 for the details.
$r \;:\!=\; \sqrt{\frac{2ka}{k+1}}$
. See Figure 1, and see Section 2 for the details.
For
![]() $k = 1,2$
, we can go a step further and determine
$k = 1,2$
, we can go a step further and determine
![]() $f(n,m)$
exactly. This is done in the following two theorems.
$f(n,m)$
exactly. This is done in the following two theorems.
Theorem 1.4.
Let
![]() $n \geq 1$
and
$n \geq 1$
and
![]() $m \leq t_2(n)$
. Then
$m \leq t_2(n)$
. Then
![]() $f(n,m) = \min \{r\;:\; t_2(r) \geq m\} - 1$
.
$f(n,m) = \min \{r\;:\; t_2(r) \geq m\} - 1$
.
For
![]() $n \geq 1$
and
$n \geq 1$
and
![]() $m \geq t_2(n)+1$
, let
$m \geq t_2(n)+1$
, let
![]() $g_2(n,m)$
be the minimum of
$g_2(n,m)$
be the minimum of
![]() $2n-t+r$
, taken over all pairs
$2n-t+r$
, taken over all pairs
![]() $t,r \geq 0$
satisfying
$t,r \geq 0$
satisfying
![]() $t(n-t) + t_2(r) \geq m$
.
$t(n-t) + t_2(r) \geq m$
.
Theorem 1.5.
Let
![]() $n \geq 1$
and
$n \geq 1$
and
![]() $t_{2}(n)+1 \leq m \leq t_{3}(n)$
. Then
$t_{2}(n)+1 \leq m \leq t_{3}(n)$
. Then
![]() $f(n,m) = g_2(n,m)-3$
.
$f(n,m) = g_2(n,m)-3$
.
The extremal construction for Theorem 1.5 is given by taking a
![]() $t \times (n-t)$
complete bipartite graph and placing a complete bipartite graph with
$t \times (n-t)$
complete bipartite graph and placing a complete bipartite graph with
![]() $r$
vertices inside the side of size
$r$
vertices inside the side of size
![]() $t$
.
$t$
.
1.1. Proof ideas
Recall that a graph is chordal if and only if it can be obtained from the one-vertex graph by repeatedly adding simplicial vertices, that is, vertices whose neighbourhood is a clique. In particular, adding simplicial vertices to a chordal graph keeps it chordal. We will often use this fact (implicitly) to claim that certain graphs are chordal.

Figure 1. The construction showing optimality of Theorem 1.3.
Let us first recall the argument used by Erdős, Gyárfás, Ordman and Zalcstein [Reference Erdős, Gyárfás, Ordman and Zalcstein9] to prove Conjecture 1.1 for
![]() $k=2$
(and
$k=2$
(and
![]() $n$
even). Let
$n$
even). Let
![]() $G$
be a graph with
$G$
be a graph with
![]() $n$
vertices and
$n$
vertices and
![]() $n^2/4+1$
edges, and let
$n^2/4+1$
edges, and let
![]() $x,y,z$
be a triangle in
$x,y,z$
be a triangle in
![]() $G$
. We need to show that
$G$
. We need to show that
![]() $G$
has a chordal subgraph
$G$
has a chordal subgraph
![]() $H$
with at least
$H$
with at least
![]() $3n/2-1$
edges. If
$3n/2-1$
edges. If
![]() $d(x) + d(y) + d(z) \geq 3n/2+2$
, then take
$d(x) + d(y) + d(z) \geq 3n/2+2$
, then take
![]() $H$
to be the subgraph consisting of all edges touching
$H$
to be the subgraph consisting of all edges touching
![]() $x,y,z$
. Suppose now that
$x,y,z$
. Suppose now that
![]() $d(x) + d(y) + d(z) \leq 3n/2+1$
. Then by averaging, we can assume without loss of generality that
$d(x) + d(y) + d(z) \leq 3n/2+1$
. Then by averaging, we can assume without loss of generality that
![]() $d(x) + d(y) \leq n$
. Deleting
$d(x) + d(y) \leq n$
. Deleting
![]() $x,y$
, we get a graph with at least
$x,y$
, we get a graph with at least
![]() $n^2/4+1 - (n-1) \geq (n-2)^2/4+1$
edges. By induction, this graph contains a chordal subgraph
$n^2/4+1 - (n-1) \geq (n-2)^2/4+1$
edges. By induction, this graph contains a chordal subgraph
![]() $H'$
with at least
$H'$
with at least
![]() $3(n-2)/2 - 1$
edges. Adding the edges
$3(n-2)/2 - 1$
edges. Adding the edges
![]() $xy,xz,yz$
gives the required chordal subgraph
$xy,xz,yz$
gives the required chordal subgraph
![]() $H$
.
$H$
.
Our proof of Theorem 1.5 is also based on this inductive argument, but with two key differences. First, we need a relation between
![]() $g_2(n,m)$
and
$g_2(n,m)$
and
![]() $g_2(n',m')$
(for
$g_2(n',m')$
(for
![]() $n' = n-2$
, say), so that the induction can be carried through when deleting vertices. And second, it turns out that the induction scheme of deleting two vertices does not work to give the correct bound on
$n' = n-2$
, say), so that the induction can be carried through when deleting vertices. And second, it turns out that the induction scheme of deleting two vertices does not work to give the correct bound on
![]() $f(n,m)$
for all
$f(n,m)$
for all
![]() $m$
in the range of Theorem 1.5. Instead, we sometimes need to delete just one vertex and then add two edges when adding the vertex back. To this end, we need to know that the deleted vertex has two neighbours which form an edge in the chordal subgraph
$m$
in the range of Theorem 1.5. Instead, we sometimes need to delete just one vertex and then add two edges when adding the vertex back. To this end, we need to know that the deleted vertex has two neighbours which form an edge in the chordal subgraph
![]() $H'$
that we find using induction. To guarantee this, we strengthen the induction hypothesis to say that not only does
$H'$
that we find using induction. To guarantee this, we strengthen the induction hypothesis to say that not only does
![]() $G$
contain a chordal subgraph with the correct number of edges, but that any given triangle in
$G$
contain a chordal subgraph with the correct number of edges, but that any given triangle in
![]() $G$
can be included in such a chordal subgraph.
$G$
can be included in such a chordal subgraph.
The idea of strengthening the induction hypothesis is also used in the proof of Theorem 1.2. Here we show that every
![]() $K_4$
can be included in a chordal subgraph with the correct number of edges. This proof has a more involved case analysis. It would be interesting to find a shorter proof.
$K_4$
can be included in a chordal subgraph with the correct number of edges. This proof has a more involved case analysis. It would be interesting to find a shorter proof.
The proof of Theorem 1.3 is based on induction as well. Here, instead of deleting only a few vertices, we delete a large number of vertices. To give the general idea, we sketch first the proof in the case
![]() $m = t_3(n) + 1$
. So let
$m = t_3(n) + 1$
. So let
![]() $G$
be a graph with
$G$
be a graph with
![]() $n$
vertices
$n$
vertices
![]() $t_3(n)+1$
edges. We need to show that
$t_3(n)+1$
edges. We need to show that
![]() $G$
has a chordal subgraph
$G$
has a chordal subgraph
![]() $H$
with at least
$H$
with at least
![]() $\frac{8n}{3} - 6 - C\sqrt{n}$
edges. Let us assume first that
$\frac{8n}{3} - 6 - C\sqrt{n}$
edges. Let us assume first that
![]() $e(G) \geq t_3(n) + 2n$
. By a theorem of Faudree [Reference Faudree12] (see also [Reference Bollobás and Nikiforov1, Reference Edwards3]), there is a triangle
$e(G) \geq t_3(n) + 2n$
. By a theorem of Faudree [Reference Faudree12] (see also [Reference Bollobás and Nikiforov1, Reference Edwards3]), there is a triangle
![]() $x,y,z \in V(G)$
with
$x,y,z \in V(G)$
with
![]() $d(x) + d(y) + d(z) \geq 6e(G)/n \geq 2n+12$
. In particular,
$d(x) + d(y) + d(z) \geq 6e(G)/n \geq 2n+12$
. In particular,
![]() $x,y,z$
have at least
$x,y,z$
have at least
![]() $12$
common neighbours. Let
$12$
common neighbours. Let
![]() $w_1,\dots,w_7$
be seven of them. If
$w_1,\dots,w_7$
be seven of them. If
![]() $d(x)+d(y)+d(z)+d(w_i) \geq \frac{8n}{3} - C\sqrt{n}$
for some
$d(x)+d(y)+d(z)+d(w_i) \geq \frac{8n}{3} - C\sqrt{n}$
for some
![]() $i$
, then take
$i$
, then take
![]() $H$
to be the subgraph consisting of all edges touching
$H$
to be the subgraph consisting of all edges touching
![]() $x,y,z,w_i$
. This
$x,y,z,w_i$
. This
![]() $H$
is chordal and
$H$
is chordal and
![]() $e(H) = d(x)+d(y)+d(z)+d(w_i) - 6$
, so we are done. Suppose then that
$e(H) = d(x)+d(y)+d(z)+d(w_i) - 6$
, so we are done. Suppose then that
![]() $d(x)+d(y)+d(z)+d(w_i) \leq \frac{8n}{3} - C\sqrt{n}$
for every
$d(x)+d(y)+d(z)+d(w_i) \leq \frac{8n}{3} - C\sqrt{n}$
for every
![]() $i$
. In particular,
$i$
. In particular,
![]() $d(w_i) \leq \frac{2n}{3} - C\sqrt{n}$
. Assume that
$d(w_i) \leq \frac{2n}{3} - C\sqrt{n}$
. Assume that
![]() $d(x) \geq d(y) \geq d(z)$
, so that
$d(x) \geq d(y) \geq d(z)$
, so that
![]() $d(x) \geq \frac{2n}{3}$
and hence
$d(x) \geq \frac{2n}{3}$
and hence
![]() $d(y) + d(z) + d(w_i) \leq 2n-C\sqrt{n}$
for each
$d(y) + d(z) + d(w_i) \leq 2n-C\sqrt{n}$
for each
![]() $i$
. Delete
$i$
. Delete
![]() $y,z,w_1,\dots,w_7$
to get a graph
$y,z,w_1,\dots,w_7$
to get a graph
![]() $G'$
on
$G'$
on
![]() $n-9$
vertices. It is easy to see that
$n-9$
vertices. It is easy to see that
![]() $e(G')$
is well above
$e(G')$
is well above
![]() $t_3(n-9)+1$
. So by the induction hypothesis, there exists a chordal subgraph
$t_3(n-9)+1$
. So by the induction hypothesis, there exists a chordal subgraph
![]() $H'$
of
$H'$
of
![]() $G'$
with
$G'$
with
![]() $e(H') \geq \frac{8(n-9)}{3} - 6 - C\sqrt{n}$
edges. Now add back the vertices
$e(H') \geq \frac{8(n-9)}{3} - 6 - C\sqrt{n}$
edges. Now add back the vertices
![]() $y,z,w_1,\dots,w_7$
, and add to
$y,z,w_1,\dots,w_7$
, and add to
![]() $H'$
the edges of the triangle
$H'$
the edges of the triangle
![]() $x,y,z$
and the edges between
$x,y,z$
and the edges between
![]() $x,y,z$
and
$x,y,z$
and
![]() $w_1,\dots,w_7$
. This is a total of
$w_1,\dots,w_7$
. This is a total of
![]() $24$
edges. So
$24$
edges. So
![]() $e(H) = e(H') + 24 \geq \frac{8n}{3} - 6 - C\sqrt{n}$
, as required. It is also easy to see that
$e(H) = e(H') + 24 \geq \frac{8n}{3} - 6 - C\sqrt{n}$
, as required. It is also easy to see that
![]() $H$
is chordal (if we add the new vertices in the order
$H$
is chordal (if we add the new vertices in the order
![]() $y,z,w_1,\dots,w_7$
, then we always add a simplicial vertex). The number
$y,z,w_1,\dots,w_7$
, then we always add a simplicial vertex). The number
![]() $7$
was chosen here so that the number of edges added would be large enough for the induction to carry through. But the key point is that such a number must exist. Indeed, each
$7$
was chosen here so that the number of edges added would be large enough for the induction to carry through. But the key point is that such a number must exist. Indeed, each
![]() $w_i$
contributes
$w_i$
contributes
![]() $3$
edges to
$3$
edges to
![]() $H$
. On the other hand, the term
$H$
. On the other hand, the term
![]() $\frac{8n}{3}$
suggests that it is enough to add
$\frac{8n}{3}$
suggests that it is enough to add
![]() $\frac{8}{3}$
edges per vertex on average. So by adding
$\frac{8}{3}$
edges per vertex on average. So by adding
![]() $3$
edges per vertex, we are gaining over the required bound.
$3$
edges per vertex, we are gaining over the required bound.
It now remains to handle the case that
![]() $e(G) \leq t_3(n) + 2n$
. Here we proceed as follows. If the minimum degree of the graph is at least
$e(G) \leq t_3(n) + 2n$
. Here we proceed as follows. If the minimum degree of the graph is at least
![]() $\frac{2n}{3} - \sqrt{n}$
, then take a 4-clique
$\frac{2n}{3} - \sqrt{n}$
, then take a 4-clique
![]() $x,y,z,w$
and take
$x,y,z,w$
and take
![]() $H$
to be the subgraph consisting of edges touching
$H$
to be the subgraph consisting of edges touching
![]() $x,y,z,w$
. Else, delete a vertex of minimum degree and continue with the remaining graph. After
$x,y,z,w$
. Else, delete a vertex of minimum degree and continue with the remaining graph. After
![]() $O(\sqrt{n})$
steps, we get a graph with
$O(\sqrt{n})$
steps, we get a graph with
![]() $n' = n - O(\sqrt{n})$
vertices and at least
$n' = n - O(\sqrt{n})$
vertices and at least
![]() $t_3(n') + 2n'$
edges, so we can apply the first case.
$t_3(n') + 2n'$
edges, so we can apply the first case.
To prove the general case of Theorem 1.3 we find a
![]() $(k-1)$
-clique
$(k-1)$
-clique
![]() $x_1,\dots,x_{k-1}$
and a forest
$x_1,\dots,x_{k-1}$
and a forest
![]() $F$
inside
$F$
inside
![]() $N(x_1,\dots,x_{k-1})$
such that
$N(x_1,\dots,x_{k-1})$
such that
![]() $F$
has few components. We delete
$F$
has few components. We delete
![]() $V(F)$
and
$V(F)$
and
![]() $x_2,\dots,x_{k-1}$
and apply induction to find a chordal subgraph
$x_2,\dots,x_{k-1}$
and apply induction to find a chordal subgraph
![]() $H'$
. We then add to
$H'$
. We then add to
![]() $H'$
the edges of the clique
$H'$
the edges of the clique
![]() $x_1,\dots,x_{k-1}$
, the edges of
$x_1,\dots,x_{k-1}$
, the edges of
![]() $F$
, and the edges between
$F$
, and the edges between
![]() $V(F)$
and
$V(F)$
and
![]() $x_1,\dots,x_{k-1}$
. Note that when adding back the vertices of
$x_1,\dots,x_{k-1}$
. Note that when adding back the vertices of
![]() $F$
one by one, most vertices contribute
$F$
one by one, most vertices contribute
![]() $k$
edges: one edge in
$k$
edges: one edge in
![]() $F$
and
$F$
and
![]() $k-1$
edges to
$k-1$
edges to
![]() $x_1,\dots,x_{k-1}$
(this fails once for each connected component of
$x_1,\dots,x_{k-1}$
(this fails once for each connected component of
![]() $F$
, and this is why we want the number of components to be small). On the other hand, the main term in Theorem 1.3 is
$F$
, and this is why we want the number of components to be small). On the other hand, the main term in Theorem 1.3 is
![]() $(k-1/k)n$
, which suggests that each vertex adds
$(k-1/k)n$
, which suggests that each vertex adds
![]() $k-1/k$
edges on average. So again we are gaining over the required bound (at least if we ignore the second term
$k-1/k$
edges on average. So again we are gaining over the required bound (at least if we ignore the second term
![]() $\sqrt{2(k+1)a/k}$
for the moment). A somewhat lengthy calculation shows that this argument indeed works for any value of
$\sqrt{2(k+1)a/k}$
for the moment). A somewhat lengthy calculation shows that this argument indeed works for any value of
![]() $a$
.
$a$
.
The rest of this short paper is organised as follows. Theorem 1.3 is proved in Section 2, Theorems 1.4 –1.5 in Section 3 and Theorem 1.2 in Section 4.
2. Proof of Theorem 1.3
In this section we prove Theorem 1.3. We begin with the upper bound. Here we use the following construction. For simplicity, assume that
![]() $n$
is divisible by
$n$
is divisible by
![]() $k,k+1$
. For general
$k,k+1$
. For general
![]() $n$
the construction is essentially the same (and, since we are only interested in an approximate result, we are allowed a small error due to divisibility issues). Fix
$n$
the construction is essentially the same (and, since we are only interested in an approximate result, we are allowed a small error due to divisibility issues). Fix
![]() $k\geq 1$
and
$k\geq 1$
and
![]() $m \leq t_{k+1}(n) = \frac{kn^2}{2(k+1)}$
, so that
$m \leq t_{k+1}(n) = \frac{kn^2}{2(k+1)}$
, so that
![]() $a \;:\!=\; m - t_k(n) \leq \frac{kn^2}{2(k+1)} - \frac{(k-1)n^2}{2k} = \frac{n^2}{2k(k+1)}$
. Set
$a \;:\!=\; m - t_k(n) \leq \frac{kn^2}{2(k+1)} - \frac{(k-1)n^2}{2k} = \frac{n^2}{2k(k+1)}$
. Set
![]() $r \;:\!=\; \sqrt{\frac{2ka}{k+1}} \leq \frac{n}{k+1}$
. Consider a complete
$r \;:\!=\; \sqrt{\frac{2ka}{k+1}} \leq \frac{n}{k+1}$
. Consider a complete
![]() $k$
-partite graph with sides
$k$
-partite graph with sides
![]() $X,Y_1,\dots,Y_{k-1}$
such that
$X,Y_1,\dots,Y_{k-1}$
such that
![]() $|X| = \frac{n + (k-1)r}{k}$
and
$|X| = \frac{n + (k-1)r}{k}$
and
![]() $|Y_i| = \frac{n-r}{k}$
for every
$|Y_i| = \frac{n-r}{k}$
for every
![]() $1 \leq i \leq k-1$
. Place an
$1 \leq i \leq k-1$
. Place an
![]() $r \times r$
complete bipartite graph with sides
$r \times r$
complete bipartite graph with sides
![]() $A,B$
inside
$A,B$
inside
![]() $X$
. This is possible as
$X$
. This is possible as
![]() $2r \leq \frac{n + (k-1)r}{k}$
. The resulting graph
$2r \leq \frac{n + (k-1)r}{k}$
. The resulting graph
![]() $G$
has
$G$
has
 \begin{eqnarray*} e(G) &=& (k-1) \cdot \frac{n + (k-1)r}{k} \cdot \frac{n-r}{k} + \binom{k-1}{2} \left ( \frac{n-r}{k} \right )^2 + r^2 = \frac{(k-1)n^2}{2k} + \frac{(k+1)r^2}{2k}\\[5pt] &=& \frac{(k-1)n^2}{2k}+a=t_k(n)+a=m. \end{eqnarray*}
\begin{eqnarray*} e(G) &=& (k-1) \cdot \frac{n + (k-1)r}{k} \cdot \frac{n-r}{k} + \binom{k-1}{2} \left ( \frac{n-r}{k} \right )^2 + r^2 = \frac{(k-1)n^2}{2k} + \frac{(k+1)r^2}{2k}\\[5pt] &=& \frac{(k-1)n^2}{2k}+a=t_k(n)+a=m. \end{eqnarray*}
Let
![]() $H$
be a chordal subgraph of
$H$
be a chordal subgraph of
![]() $G$
. We have
$G$
. We have
![]() $e_H(A,B) \leq |A| + |B| - 1 = 2r-1$
,
$e_H(A,B) \leq |A| + |B| - 1 = 2r-1$
,
![]() $e_H(A,Y_i) \leq |A| + |Y_i| - 1$
,
$e_H(A,Y_i) \leq |A| + |Y_i| - 1$
,
![]() $e_H(X\setminus A,Y_i) \leq |X| - |A| + |Y_i| - 1$
and
$e_H(X\setminus A,Y_i) \leq |X| - |A| + |Y_i| - 1$
and
![]() $e_H(Y_i,Y_j) \leq |Y_i| + |Y_j| - 1$
, because each of these bipartite graphs is induced in
$e_H(Y_i,Y_j) \leq |Y_i| + |Y_j| - 1$
, because each of these bipartite graphs is induced in
![]() $G$
, so its intersection with
$G$
, so its intersection with
![]() $H$
is a forest. So
$H$
is a forest. So
 \begin{align*} e(H) &\leq 2r-1 + (k-1)|X| - 2(k-1) + 2\sum _{i = 1}^{k-1}{|Y_i|} + \sum _{1 \leq i \lt j \leq k-1}(|Y_i| + |Y_j| - 1) \\[5pt] &= kn - |X| + 2r - \binom{k+1}{2} = (k-1/k)n + \frac{(k+1)r}{k} - \binom{k+1}{2} \\[5pt] &= (k-1/k)n + \sqrt{2(k+1)a/k} - \binom{k+1}{2}, \end{align*}
\begin{align*} e(H) &\leq 2r-1 + (k-1)|X| - 2(k-1) + 2\sum _{i = 1}^{k-1}{|Y_i|} + \sum _{1 \leq i \lt j \leq k-1}(|Y_i| + |Y_j| - 1) \\[5pt] &= kn - |X| + 2r - \binom{k+1}{2} = (k-1/k)n + \frac{(k+1)r}{k} - \binom{k+1}{2} \\[5pt] &= (k-1/k)n + \sqrt{2(k+1)a/k} - \binom{k+1}{2}, \end{align*}
giving the upper bound on
![]() $f(n,m)$
for Theorem 1.3. We now prove the lower bound, which we restate for convenience as follows.
$f(n,m)$
for Theorem 1.3. We now prove the lower bound, which we restate for convenience as follows.
Theorem 2.1.
For every
![]() $k \geq 1$
there is
$k \geq 1$
there is
![]() $C = C(k)$
such that the following holds. Let
$C = C(k)$
such that the following holds. Let
![]() $n,a \geq 1$
, and let
$n,a \geq 1$
, and let
![]() $G$
be a graph with
$G$
be a graph with
![]() $n$
vertices and at least
$n$
vertices and at least
![]() $t_k(n) + a$
edges. Then
$t_k(n) + a$
edges. Then
![]() $G$
has a chordal subgraph with at least
$G$
has a chordal subgraph with at least
![]() $(k-1/k)n + \sqrt{2(k+1)a/k} - C\sqrt{n} - \binom{k+1}{2}$
edges.
$(k-1/k)n + \sqrt{2(k+1)a/k} - C\sqrt{n} - \binom{k+1}{2}$
edges.
For the proof of Theorem 2.1 we need two lemmas. The following lemma uses an argument originally used by Edwards [Reference Edwards3, Reference Edwards4] and Faudree [Reference Faudree12] (see also [Reference Bollobás and Nikiforov1]) to find cliques with a large degree sum.
Lemma 2.2.
Let
![]() $k,n,a \geq 1$
and let
$k,n,a \geq 1$
and let
![]() $G$
be a graph with
$G$
be a graph with
![]() $n$
vertices and at least
$n$
vertices and at least
![]() $\frac{(k-1)n^2}{2k} + a$
edges. Consider the following process: for
$\frac{(k-1)n^2}{2k} + a$
edges. Consider the following process: for
![]() $i =1,2,\dots$
, take
$i =1,2,\dots$
, take
![]() $x_i$
to be a vertex of maximum degree among all vertices in
$x_i$
to be a vertex of maximum degree among all vertices in
![]() $N(x_1,\dots,x_{i-1})$
. Then this process continues for at least
$N(x_1,\dots,x_{i-1})$
. Then this process continues for at least
![]() $k$
steps, and
$k$
steps, and
![]() $N(x_1,\dots,x_{k-1})$
contains at least
$N(x_1,\dots,x_{k-1})$
contains at least
![]() $a$
edges.
$a$
edges.
Proof. We prove the lemma by induction on
![]() $k$
. The base case
$k$
. The base case
![]() $k=1$
is trivial. Let
$k=1$
is trivial. Let
![]() $k \geq 2$
. By the induction hypothesis, the process continues for at least
$k \geq 2$
. By the induction hypothesis, the process continues for at least
![]() $k-1$
steps. It remains to show that
$k-1$
steps. It remains to show that
![]() $N(x_1,\dots,x_{k-1})$
contains at least
$N(x_1,\dots,x_{k-1})$
contains at least
![]() $a$
edges, because this would also imply that
$a$
edges, because this would also imply that
![]() $N(x_1,\dots,x_{k-1}) \neq \emptyset$
and hence the process continues for at least
$N(x_1,\dots,x_{k-1}) \neq \emptyset$
and hence the process continues for at least
![]() $k$
steps. For
$k$
steps. For
![]() $1 \leq i \leq k-1$
, let
$1 \leq i \leq k-1$
, let
![]() $S_i$
be the set of vertices which are adjacent to
$S_i$
be the set of vertices which are adjacent to
![]() $x_1,\dots,x_{i-1}$
but not adjacent to
$x_1,\dots,x_{i-1}$
but not adjacent to
![]() $x_i$
. In particular,
$x_i$
. In particular,
![]() $S_1$
is just the set of vertices not adjacent to
$S_1$
is just the set of vertices not adjacent to
![]() $x_1$
and
$x_1$
and
![]() $x_i \in S_i$
for all
$x_i \in S_i$
for all
![]() $i$
. Then
$i$
. Then
![]() $V(G) = S_1 \cup \dots \cup S_{k-1} \cup N(x_1,\dots,x_{k-1})$
. Put
$V(G) = S_1 \cup \dots \cup S_{k-1} \cup N(x_1,\dots,x_{k-1})$
. Put
![]() $S \;:\!=\; S_1 \cup \dots \cup S_{k-1}$
,
$S \;:\!=\; S_1 \cup \dots \cup S_{k-1}$
,
![]() $N \;:\!=\; N(x_1,\dots,x_{k-1})$
,
$N \;:\!=\; N(x_1,\dots,x_{k-1})$
,
![]() $s_i \;:\!=\; |S_i|$
,
$s_i \;:\!=\; |S_i|$
,
![]() $s = |S|$
and
$s = |S|$
and
![]() $d_i \;:\!=\; d(x_i)$
. Note that
$d_i \;:\!=\; d(x_i)$
. Note that
![]() $s_i \leq n - d_i$
. Also, all vertices in
$s_i \leq n - d_i$
. Also, all vertices in
![]() $S_i$
have degree at most
$S_i$
have degree at most
![]() $d_i$
. We have
$d_i$
. We have
 \begin{equation} e(N,S) + 2e(S) = \sum _{v \in S}d(v) \leq \sum _{i = 1}^{k-1}{s_i \cdot d_i} \leq \sum _{i=1}^{k-1}{s_i(n-s_i)}. \end{equation}
\begin{equation} e(N,S) + 2e(S) = \sum _{v \in S}d(v) \leq \sum _{i = 1}^{k-1}{s_i \cdot d_i} \leq \sum _{i=1}^{k-1}{s_i(n-s_i)}. \end{equation}
Since
![]() $e(G) = e(N) + e(S) + e(N,S)$
, we have
$e(G) = e(N) + e(S) + e(N,S)$
, we have
![]() $2e(S) = 2e(G) - 2e(N) - 2e(N,S)$
. Plugging this into (1) and rearranging, we get
$2e(S) = 2e(G) - 2e(N) - 2e(N,S)$
. Plugging this into (1) and rearranging, we get
 \begin{equation} e(N) \geq e(G) - \frac{1}{2}e(N,S) - \frac{1}{2} \cdot \sum _{i = 1}^{k-1}{s_i(n-s_i)}. \end{equation}
\begin{equation} e(N) \geq e(G) - \frac{1}{2}e(N,S) - \frac{1}{2} \cdot \sum _{i = 1}^{k-1}{s_i(n-s_i)}. \end{equation}
We have
![]() $e(N,S) \leq |N| \cdot |S| = (n - s)s$
. Also, by Cauchy–Schwarz,
$e(N,S) \leq |N| \cdot |S| = (n - s)s$
. Also, by Cauchy–Schwarz,
 \begin{equation*}\sum _{i = 1}^{k-1}{s_i(n-s_i)} = ns - \sum _{i=1}^{k-1}{s_i^2} \leq ns - \frac {s^2}{k-1}. \end{equation*}
\begin{equation*}\sum _{i = 1}^{k-1}{s_i(n-s_i)} = ns - \sum _{i=1}^{k-1}{s_i^2} \leq ns - \frac {s^2}{k-1}. \end{equation*}
Plugging this into (2) gives
The maximum of
![]() $ns - \frac{ks^2}{2(k-1)}$
is obtained at
$ns - \frac{ks^2}{2(k-1)}$
is obtained at
![]() $s = \frac{(k-1)n}{k}$
and equals
$s = \frac{(k-1)n}{k}$
and equals
![]() $\frac{(k-1)n^2}{2k}$
. Hence,
$\frac{(k-1)n^2}{2k}$
. Hence,
![]() $e(N) \geq e(G) - \frac{(k-1)n^2}{2k} \geq a$
, as required.
$e(N) \geq e(G) - \frac{(k-1)n^2}{2k} \geq a$
, as required.
Lemma 2.3.
Let
![]() $G$
be a graph with
$G$
be a graph with
![]() $n$
vertices and
$n$
vertices and
![]() $a$
edges. Let
$a$
edges. Let
![]() $s \geq 1$
and suppose that
$s \geq 1$
and suppose that
![]() $a \geq 2s^2$
. Then
$a \geq 2s^2$
. Then
![]() $G$
contains a forest
$G$
contains a forest
![]() $F$
with
$F$
with
![]() $s$
vertices and at least
$s$
vertices and at least
![]() $s - 1 - \frac{sn}{a}$
edges.
$s - 1 - \frac{sn}{a}$
edges.
Proof. Let
![]() $C_1,\dots,C_m$
be the connected components of
$C_1,\dots,C_m$
be the connected components of
![]() $G$
with
$G$
with
![]() $|C_1| \geq \dots \geq |C_m|$
. Let
$|C_1| \geq \dots \geq |C_m|$
. Let
![]() $\ell \geq 1$
be the minimal integer satisfying
$\ell \geq 1$
be the minimal integer satisfying
![]() $|C_1| + \dots + |C_{\ell }| \geq s$
. If
$|C_1| + \dots + |C_{\ell }| \geq s$
. If
![]() $\ell \leq 1 + \frac{sn}{a}$
then take
$\ell \leq 1 + \frac{sn}{a}$
then take
![]() $F$
to be a forest contained in
$F$
to be a forest contained in
![]() $C_1 \cup \dots \cup C_{\ell }$
having
$C_1 \cup \dots \cup C_{\ell }$
having
![]() $s$
vertices and
$s$
vertices and
![]() $\ell$
connected components. Suppose now by contradiction that
$\ell$
connected components. Suppose now by contradiction that
![]() $\ell \gt 1 + \frac{sn}{a}$
. Set
$\ell \gt 1 + \frac{sn}{a}$
. Set
![]() $r = |C_1| + \dots + |C_{\ell -1}|$
. Then
$r = |C_1| + \dots + |C_{\ell -1}|$
. Then
![]() $r \lt s$
and
$r \lt s$
and
![]() $|C_{\ell -1}| \leq \frac{r}{\ell -1}$
. We have
$|C_{\ell -1}| \leq \frac{r}{\ell -1}$
. We have
![]() $e(G) \leq \binom{r}{2} + \sum _{i = \ell }^{m}{\binom{|C_i|}{2}}$
. By convexity, the sum
$e(G) \leq \binom{r}{2} + \sum _{i = \ell }^{m}{\binom{|C_i|}{2}}$
. By convexity, the sum
![]() $\sum _{i = \ell }^{m}{\binom{|C_i|}{2}}$
is maximised when all except maybe one of the
$\sum _{i = \ell }^{m}{\binom{|C_i|}{2}}$
is maximised when all except maybe one of the
![]() $|C_i|$
’s are equal to their maximal value, which is
$|C_i|$
’s are equal to their maximal value, which is
![]() $\frac{r}{\ell -1}$
. So
$\frac{r}{\ell -1}$
. So
 \begin{align*} e(G) \leq \binom{r}{2} + \left \lceil \frac{n-r}{r/(\ell -1)} \right \rceil \cdot \binom{r/(\ell -1)}{2} &\leq \binom{r}{2} + \left ( 1 + \frac{n-r}{r/(\ell -1)} \right ) \cdot \binom{r/(\ell -1)}{2} \\[5pt] &\leq \binom{r}{2} + \binom{r/(\ell -1)}{2} + \frac{nr}{2(\ell -1)} \\[5pt] &\lt 2\binom{s}{2} + \frac{sn}{2sn/a} \leq a, \end{align*}
\begin{align*} e(G) \leq \binom{r}{2} + \left \lceil \frac{n-r}{r/(\ell -1)} \right \rceil \cdot \binom{r/(\ell -1)}{2} &\leq \binom{r}{2} + \left ( 1 + \frac{n-r}{r/(\ell -1)} \right ) \cdot \binom{r/(\ell -1)}{2} \\[5pt] &\leq \binom{r}{2} + \binom{r/(\ell -1)}{2} + \frac{nr}{2(\ell -1)} \\[5pt] &\lt 2\binom{s}{2} + \frac{sn}{2sn/a} \leq a, \end{align*}
where the last inequality uses
![]() $a \geq 2s^2$
. We got a contradiction to
$a \geq 2s^2$
. We got a contradiction to
![]() $e(G) = a$
.
$e(G) = a$
.
We are now ready to prove Theorem 2.1. An overview of the proof can be found in Section 1.1.
Proof of Theorem
2.1
. The proof is by induction on
![]() $n$
. Fix constants
$n$
. Fix constants
![]() $k \ll c \ll c_1 \ll C$
, to be chosen implicitly later. Suppose first that
$k \ll c \ll c_1 \ll C$
, to be chosen implicitly later. Suppose first that
![]() $a \leq (ck + 1)^2n$
. In this case we proceed as follows. If
$a \leq (ck + 1)^2n$
. In this case we proceed as follows. If
![]() $\delta (G) \geq \lfloor \frac{(k-1)n}{k} \rfloor - c_1\sqrt{n}$
, then take a
$\delta (G) \geq \lfloor \frac{(k-1)n}{k} \rfloor - c_1\sqrt{n}$
, then take a
![]() $(k+1)$
-clique
$(k+1)$
-clique
![]() $x_1,\dots,x_{k+1} \in V(G)$
and take
$x_1,\dots,x_{k+1} \in V(G)$
and take
![]() $H$
to consist of all edges that touch
$H$
to consist of all edges that touch
![]() $x_1,\dots,x_{k+1}$
. Then
$x_1,\dots,x_{k+1}$
. Then
![]() $H$
is chordal and
$H$
is chordal and
 \begin{align*} e(H) &= \sum _{i=1}^{k+1}{d(x_i)} - \binom{k+1}{2} \geq (k+1) \cdot \left ( \frac{(k-1)n}{k} - 2c_1\sqrt{n} \right ) - \binom{k+1}{2} \\[5pt] &= (k-1/k)n - 2(k+1)c_1\sqrt{n} - \binom{k+1}{2} \geq (k-1/k)n + \sqrt{2(k+1)a/k} - C\sqrt{n} - \binom{k+1}{2}, \end{align*}
\begin{align*} e(H) &= \sum _{i=1}^{k+1}{d(x_i)} - \binom{k+1}{2} \geq (k+1) \cdot \left ( \frac{(k-1)n}{k} - 2c_1\sqrt{n} \right ) - \binom{k+1}{2} \\[5pt] &= (k-1/k)n - 2(k+1)c_1\sqrt{n} - \binom{k+1}{2} \geq (k-1/k)n + \sqrt{2(k+1)a/k} - C\sqrt{n} - \binom{k+1}{2}, \end{align*}
where the last inequality holds as
![]() $C \gg c_1,c$
and
$C \gg c_1,c$
and
![]() $a \leq (ck + 1)^2n$
. Suppose now that there is
$a \leq (ck + 1)^2n$
. Suppose now that there is
![]() $v \in V(G)$
with
$v \in V(G)$
with
![]() $d(v) \leq \lfloor \frac{(k-1)n}{k}\rfloor - c_1\sqrt{n}$
. Let
$d(v) \leq \lfloor \frac{(k-1)n}{k}\rfloor - c_1\sqrt{n}$
. Let
![]() $G' = G - v$
. Then
$G' = G - v$
. Then
By the induction hypothesis with parameter
![]() $a' = a + c_1\sqrt{n}$
,
$a' = a + c_1\sqrt{n}$
,
![]() $G'$
contains a chordal subgraph
$G'$
contains a chordal subgraph
![]() $H'$
with
$H'$
with
As
![]() $(k-1/k)(n-1) \geq (k-1/k)n - k$
, it suffices to show that
$(k-1/k)(n-1) \geq (k-1/k)n - k$
, it suffices to show that
![]() $\sqrt{2(k+1)a'/k} \geq \sqrt{2(k+1)a/k} + k$
. Squaring and plugging in the value of
$\sqrt{2(k+1)a'/k} \geq \sqrt{2(k+1)a/k} + k$
. Squaring and plugging in the value of
![]() $a'$
, we get
$a'$
, we get
Cancelling the term
![]() $2(k+1)a/k$
from both sides and rearranging, we see that it is enough to have
$2(k+1)a/k$
from both sides and rearranging, we see that it is enough to have
which holds because
![]() $a \leq (ck + 1)^2n$
and
$a \leq (ck + 1)^2n$
and
![]() $c_1 \gg c$
.
$c_1 \gg c$
.
For the rest of the proof we assume that
![]() $a \geq (ck + 1)^2n$
. Note that
$a \geq (ck + 1)^2n$
. Note that
![]() $e(G) \geq t_k(n) + a \geq \frac{(k-1)n^2}{2k} + \frac{a}{2}$
because
$e(G) \geq t_k(n) + a \geq \frac{(k-1)n^2}{2k} + \frac{a}{2}$
because
![]() $t_k(n) \geq \frac{(k-1)n^2}{2k} - O_k(1)$
and
$t_k(n) \geq \frac{(k-1)n^2}{2k} - O_k(1)$
and
![]() $a \geq c \gg k$
. Let
$a \geq c \gg k$
. Let
![]() $x_1,\dots,x_{k-1}$
be as in Lemma 2.2 and put
$x_1,\dots,x_{k-1}$
be as in Lemma 2.2 and put
![]() $N = N(x_1,\dots,x_{k-1})$
. By Lemma 2.2 we have
$N = N(x_1,\dots,x_{k-1})$
. By Lemma 2.2 we have
![]() $e(N) \geq \frac{a}{2}$
. Also, the choice of
$e(N) \geq \frac{a}{2}$
. Also, the choice of
![]() $x_1,\dots,x_{k-1}$
in Lemma 2.2 implies that
$x_1,\dots,x_{k-1}$
in Lemma 2.2 implies that
![]() $d(y) \leq d(x_{k-1}) \leq \dots \leq d(x_1)$
for every
$d(y) \leq d(x_{k-1}) \leq \dots \leq d(x_1)$
for every
![]() $y \in N$
. For convenience, we set
$y \in N$
. For convenience, we set
 \begin{equation*} d_0 \;:\!=\; \frac {(k-1)n}{k} + \sqrt {\frac {2a}{k(k+1)}} - c\sqrt {n}. \end{equation*}
\begin{equation*} d_0 \;:\!=\; \frac {(k-1)n}{k} + \sqrt {\frac {2a}{k(k+1)}} - c\sqrt {n}. \end{equation*}
Note that
![]() $d_0 \geq \frac{(k-1)n}{k}$
by our assumption that
$d_0 \geq \frac{(k-1)n}{k}$
by our assumption that
![]() $a \geq (ck + 1)^2n$
.
$a \geq (ck + 1)^2n$
.
Claim 2.4.
If the statement of the theorem does not hold, then
![]() $G[N]$
contains a forest
$G[N]$
contains a forest
![]() $F$
with
$F$
with
![]() $v(F) = \lfloor \sqrt{n} \rfloor$
,
$v(F) = \lfloor \sqrt{n} \rfloor$
,
![]() $e(F)\geq v(F) - 1 - \frac{2n^{3/2}}{a}$
, and
$e(F)\geq v(F) - 1 - \frac{2n^{3/2}}{a}$
, and
Proof. We consider two cases. Suppose first that there is
![]() $x_k \in N$
such that
$x_k \in N$
such that
![]() $d(x_k) \geq d_0$
. Then
$d(x_k) \geq d_0$
. Then
![]() $d(x_i) \geq d_0$
for every
$d(x_i) \geq d_0$
for every
![]() $1 \leq i \leq k-1$
. Hence,
$1 \leq i \leq k-1$
. Hence,
![]() $d(x_1) + \dots + d(x_k) \geq k \cdot d_0$
. This means that
$d(x_1) + \dots + d(x_k) \geq k \cdot d_0$
. This means that
![]() $x_1,\dots,x_k$
have at least
$x_1,\dots,x_k$
have at least
 \begin{equation*} kd_0 - (k-1)n = \sqrt {\frac {2ka}{(k+1)}} - ck\sqrt {n} \geq \sqrt {a} - ck\sqrt {n} \geq \sqrt {n} \end{equation*}
\begin{equation*} kd_0 - (k-1)n = \sqrt {\frac {2ka}{(k+1)}} - ck\sqrt {n} \geq \sqrt {a} - ck\sqrt {n} \geq \sqrt {n} \end{equation*}
common neighbours, where the last inequality holds by the assumption
![]() $a \geq (ck + 1)^2n$
. Take
$a \geq (ck + 1)^2n$
. Take
![]() $F$
to be the star whose centre is
$F$
to be the star whose centre is
![]() $x_k$
and whose leaves are
$x_k$
and whose leaves are
![]() $\lfloor \sqrt{n} \rfloor - 1$
common neighbours of
$\lfloor \sqrt{n} \rfloor - 1$
common neighbours of
![]() $x_1,\dots,x_k$
. Let
$x_1,\dots,x_k$
. Let
![]() $y \in N(x_1,\dots,x_k)$
. If
$y \in N(x_1,\dots,x_k)$
. If
![]() $d(y) \geq d_0$
then
$d(y) \geq d_0$
then
and then the subgraph consisting of all edges touching
![]() $\{x_1,\dots,x_k,y\}$
is a chordal graph with at least
$\{x_1,\dots,x_k,y\}$
is a chordal graph with at least
![]() $(k- 1/k)n + \sqrt{2(k+1)a/k} - (k+1)c\sqrt{n} - \binom{k+1}{2}$
edges, so the assertion of the theorem holds. Hence, we may assume that
$(k- 1/k)n + \sqrt{2(k+1)a/k} - (k+1)c\sqrt{n} - \binom{k+1}{2}$
edges, so the assertion of the theorem holds. Hence, we may assume that
![]() $d(y) \leq d_0$
for every
$d(y) \leq d_0$
for every
![]() $y \in N(x_1,\dots,x_k)$
. This means that
$y \in N(x_1,\dots,x_k)$
. This means that
as required by the claim. Also,
![]() $F$
has the right number of edges, as
$F$
has the right number of edges, as
![]() $e(F)=v(F)-1$
.
$e(F)=v(F)-1$
.
The second case is that
![]() $d(y) \leq d_0$
for every
$d(y) \leq d_0$
for every
![]() $y \in N$
. Since
$y \in N$
. Since
![]() $e(N) \geq \frac{a}{2} \geq 2n$
, we can apply Lemma 2.3 to
$e(N) \geq \frac{a}{2} \geq 2n$
, we can apply Lemma 2.3 to
![]() $G[N]$
with parameters
$G[N]$
with parameters
![]() $\frac{a}{2}$
and
$\frac{a}{2}$
and
![]() $s = \lfloor \sqrt{n} \rfloor$
to obtain a forest
$s = \lfloor \sqrt{n} \rfloor$
to obtain a forest
![]() $F$
with
$F$
with
![]() $\lfloor \sqrt{n} \rfloor$
vertices and at least
$\lfloor \sqrt{n} \rfloor$
vertices and at least
![]() $v(F) - 1 - \frac{2n^{3/2}}{a}$
edges. All vertices in
$v(F) - 1 - \frac{2n^{3/2}}{a}$
edges. All vertices in
![]() $F$
have degree at most
$F$
have degree at most
![]() $d_0$
, so (3) holds.
$d_0$
, so (3) holds.
We continue with the proof of the theorem. Let
![]() $F$
be the forest given by Claim 2.4. Let
$F$
be the forest given by Claim 2.4. Let
![]() $G'$
be the graph obtained from
$G'$
be the graph obtained from
![]() $G$
by deleting the
$G$
by deleting the
![]() $t \;:\!=\; k-2 + v(F)$
vertices
$t \;:\!=\; k-2 + v(F)$
vertices
![]() $T \;:\!=\; \{ x_2,\dots,x_{k-1} \} \cup V(F)$
. By (3), we have
$T \;:\!=\; \{ x_2,\dots,x_{k-1} \} \cup V(F)$
. By (3), we have
where the second inequality uses that
![]() $d_0 \geq \frac{(k-1)n}{k}$
. As
$d_0 \geq \frac{(k-1)n}{k}$
. As
![]() $e(G) \geq t_k(n) + a \geq \frac{(k-1)n^2}{2k} - O_k(1) + a$
, we have that
$e(G) \geq t_k(n) + a \geq \frac{(k-1)n^2}{2k} - O_k(1) + a$
, we have that
 \begin{align*} e(G') \geq e(G) - t \cdot d_0 - n &\geq \frac{(k-1)n^2}{2k}- O_k(1) + a - t \cdot d_0 - n \\[5pt] &= \frac{(k-1)(n-t)^2}{2k} + \frac{(k-1)nt}{k} - \frac{(k-1)t^2}{2k} - O_k(1) + a - t \cdot d_0 - n \\[5pt] &= \frac{(k-1)(n-t)^2}{2k} - O_k(1) + a - \frac{(k-1)t^2}{2k} - t \cdot \sqrt{\frac{2a}{k(k+1)}} + ct\sqrt{n} - n \\[5pt] &\geq t_k(n-t) + a - \frac{(k-1)t^2}{2k} - t \cdot \sqrt{\frac{2a}{k(k+1)}} + \frac{c}{2}t\sqrt{n}, \end{align*}
\begin{align*} e(G') \geq e(G) - t \cdot d_0 - n &\geq \frac{(k-1)n^2}{2k}- O_k(1) + a - t \cdot d_0 - n \\[5pt] &= \frac{(k-1)(n-t)^2}{2k} + \frac{(k-1)nt}{k} - \frac{(k-1)t^2}{2k} - O_k(1) + a - t \cdot d_0 - n \\[5pt] &= \frac{(k-1)(n-t)^2}{2k} - O_k(1) + a - \frac{(k-1)t^2}{2k} - t \cdot \sqrt{\frac{2a}{k(k+1)}} + ct\sqrt{n} - n \\[5pt] &\geq t_k(n-t) + a - \frac{(k-1)t^2}{2k} - t \cdot \sqrt{\frac{2a}{k(k+1)}} + \frac{c}{2}t\sqrt{n}, \end{align*}
where the last inequality uses that
![]() $t \geq \lfloor \sqrt{n} \rfloor$
and
$t \geq \lfloor \sqrt{n} \rfloor$
and
![]() $c \gg k$
, so that
$c \gg k$
, so that
![]() $\frac{c}{2}t\sqrt{n} \geq O_k(1) + n$
. Set
$\frac{c}{2}t\sqrt{n} \geq O_k(1) + n$
. Set
 \begin{equation*}\label {eq:r'} a' \;:\!=\; a - \frac {(k-1)t^2}{2k} - t \cdot \sqrt {\frac {2a}{k(k+1)}} + \frac {c}{2}t\sqrt {n}, \end{equation*}
\begin{equation*}\label {eq:r'} a' \;:\!=\; a - \frac {(k-1)t^2}{2k} - t \cdot \sqrt {\frac {2a}{k(k+1)}} + \frac {c}{2}t\sqrt {n}, \end{equation*}
so that
![]() $e(G') \geq t_k(n-t)+a'$
. We have
$e(G') \geq t_k(n-t)+a'$
. We have
![]() $a' \geq 1$
because
$a' \geq 1$
because
![]() $t \leq \sqrt{n}+k-2$
,
$t \leq \sqrt{n}+k-2$
,
![]() $a \geq c^2n$
(say) and
$a \geq c^2n$
(say) and
![]() $c \gg k$
. By the induction hypothesis,
$c \gg k$
. By the induction hypothesis,
![]() $G'$
contains a chordal subgraph
$G'$
contains a chordal subgraph
![]() $H'$
of size at least
$H'$
of size at least
Let
![]() $H$
be the subgraph of
$H$
be the subgraph of
![]() $G$
obtained by adding to
$G$
obtained by adding to
![]() $H'$
the edges of the clique
$H'$
the edges of the clique
![]() $x_1,\dots,x_{k-1}$
, the edges between
$x_1,\dots,x_{k-1}$
, the edges between
![]() $x_1,\dots,x_{k-1}$
and
$x_1,\dots,x_{k-1}$
and
![]() $V(F)$
, and the edges of
$V(F)$
, and the edges of
![]() $F$
. Then
$F$
. Then
![]() $H$
is chordal. To complete the proof, it suffices to verify that
$H$
is chordal. To complete the proof, it suffices to verify that
By the definition of
![]() $H$
, we have
$H$
, we have
Note that
and therefore,
For convenience, set
![]() $h \;:\!=\; \frac{(k+1)(k-2)}{2} + 1 + \frac{2n^{3/2}}{a}$
. Then,
$h \;:\!=\; \frac{(k+1)(k-2)}{2} + 1 + \frac{2n^{3/2}}{a}$
. Then,
So it remains to verify that the right-hand side of (4) is at least as large as
Cancel the terms
![]() $(k-1/k)n$
,
$(k-1/k)n$
,
![]() $\binom{k+1}{2}$
which appear in both expressions. Also, we may drop the terms
$\binom{k+1}{2}$
which appear in both expressions. Also, we may drop the terms
![]() $C\sqrt{n-t}$
,
$C\sqrt{n-t}$
,
![]() $C\sqrt{n}$
. After rearranging, we get the inequality
$C\sqrt{n}$
. After rearranging, we get the inequality
By squaring and plugging in the value of
![]() $a'$
, we get:
$a'$
, we get:
 \begin{equation} \begin{split} & \frac{2(k+1)}{k} \cdot \left ( a - \frac{(k-1)t^2}{2k} - t \cdot \sqrt{\frac{2a}{k(k+1)}} + \frac{c}{2}t\sqrt{n} \right ) \geq \\[5pt] &\frac{2(k+1)a}{k} + \frac{t^2}{k^2} + h^2 - \frac{2t}{k} \cdot \sqrt{\frac{2(k+1)a}{k}} + 2h \cdot \sqrt{\frac{2(k+1)a}{k}} - \frac{2th}{k}. \end{split} \end{equation}
\begin{equation} \begin{split} & \frac{2(k+1)}{k} \cdot \left ( a - \frac{(k-1)t^2}{2k} - t \cdot \sqrt{\frac{2a}{k(k+1)}} + \frac{c}{2}t\sqrt{n} \right ) \geq \\[5pt] &\frac{2(k+1)a}{k} + \frac{t^2}{k^2} + h^2 - \frac{2t}{k} \cdot \sqrt{\frac{2(k+1)a}{k}} + 2h \cdot \sqrt{\frac{2(k+1)a}{k}} - \frac{2th}{k}. \end{split} \end{equation}
Both sides of the inequality (5) have the terms
![]() $\frac{2(k+1)}{k}a$
and
$\frac{2(k+1)}{k}a$
and
![]() $-\frac{2t}{k} \cdot \sqrt{\frac{2(k+1)a}{k}}$
. We can also drop the negative term
$-\frac{2t}{k} \cdot \sqrt{\frac{2(k+1)a}{k}}$
. We can also drop the negative term
![]() $\frac{2th}{k}$
on the right-hand side. After rearranging, we get the inequality
$\frac{2th}{k}$
on the right-hand side. After rearranging, we get the inequality
We have
![]() $t \leq \sqrt{n} + k$
and
$t \leq \sqrt{n} + k$
and
![]() $h \leq O_k(1) + \frac{2n^{3/2}}{a} \leq O_k(1) + \sqrt{n}$
, so
$h \leq O_k(1) + \frac{2n^{3/2}}{a} \leq O_k(1) + \sqrt{n}$
, so
![]() $t^2,h^2 \leq O_k(n)$
. Also,
$t^2,h^2 \leq O_k(n)$
. Also,
as
![]() $n \leq a \leq n^2$
. So the right-hand side of (6) is
$n \leq a \leq n^2$
. So the right-hand side of (6) is
![]() $O_k(n)$
. On the other hand, the left-hand side is larger than
$O_k(n)$
. On the other hand, the left-hand side is larger than
![]() $\frac{cn}{2}$
because
$\frac{cn}{2}$
because
![]() $t \geq \lfloor \sqrt{n}\rfloor \geq \sqrt{n}/2$
. So (6) holds because
$t \geq \lfloor \sqrt{n}\rfloor \geq \sqrt{n}/2$
. So (6) holds because
![]() $c \gg k$
, as required.
$c \gg k$
, as required.
3. Proof of Theorems 1.4 and 1.5
Proof of Theorem
1.4
. For the upper bound, let
![]() $r \geq 1$
be the minimal integer satisfying
$r \geq 1$
be the minimal integer satisfying
![]() $t_2(r) \geq m$
and take
$t_2(r) \geq m$
and take
![]() $G$
to be
$G$
to be
![]() $T_2(r)$
with
$T_2(r)$
with
![]() $n-r$
isolated vertices. Then
$n-r$
isolated vertices. Then
![]() $e(G) \geq m$
, but every chordal subgraph of
$e(G) \geq m$
, but every chordal subgraph of
![]() $G$
has at most
$G$
has at most
![]() $r-1$
edges. For the lower bound, we prove by induction on the number of vertices that every graph
$r-1$
edges. For the lower bound, we prove by induction on the number of vertices that every graph
![]() $G$
with
$G$
with
![]() $m$
edges has a chordal subgraph
$m$
edges has a chordal subgraph
![]() $H$
with at least
$H$
with at least
![]() $g_1(m)-1$
edges, where
$g_1(m)-1$
edges, where
![]() $g_1(m) \;:\!=\; \min _{r: t_2(r) \geq m} r$
. For
$g_1(m) \;:\!=\; \min _{r: t_2(r) \geq m} r$
. For
![]() $m = 0$
, the assertion is trivial. Suppose
$m = 0$
, the assertion is trivial. Suppose
![]() $m \geq 1$
and let
$m \geq 1$
and let
![]() $xy \in E(G)$
. Fix
$xy \in E(G)$
. Fix
![]() $r$
such that
$r$
such that
![]() $g_1(m) = r$
. If
$g_1(m) = r$
. If
![]() $d(x) + d(y) \geq r$
then take
$d(x) + d(y) \geq r$
then take
![]() $H$
to be the subgraph consisting of all edges touching
$H$
to be the subgraph consisting of all edges touching
![]() $x,y$
. This graph is chordal and has
$x,y$
. This graph is chordal and has
![]() $d(x)+d(y)-1$
edges. Suppose now that
$d(x)+d(y)-1$
edges. Suppose now that
![]() $d(x) + d(y) \leq r-1$
; without loss of generality,
$d(x) + d(y) \leq r-1$
; without loss of generality,
![]() $d(x) \leq \lfloor \frac{r-1}{2} \rfloor$
. Let
$d(x) \leq \lfloor \frac{r-1}{2} \rfloor$
. Let
![]() $G' = G-x$
. Then
$G' = G-x$
. Then
![]() $e(G') = m - d(x) \geq m - \lfloor \frac{r-1}{2} \rfloor$
. We claim that
$e(G') = m - d(x) \geq m - \lfloor \frac{r-1}{2} \rfloor$
. We claim that
![]() $e(G') \gt t_2(r-2)$
. Indeed, if
$e(G') \gt t_2(r-2)$
. Indeed, if
![]() $e(G') \leq t_2(r-2)$
then
$e(G') \leq t_2(r-2)$
then
![]() $m \leq t_2(r-2) + \lfloor \frac{r-1}{2} \rfloor = t_2(r-1)$
, in contradiction to the choice of
$m \leq t_2(r-2) + \lfloor \frac{r-1}{2} \rfloor = t_2(r-1)$
, in contradiction to the choice of
![]() $r$
. So
$r$
. So
![]() $g_1(e(G')) \geq r-1$
. By the induction hypothesis,
$g_1(e(G')) \geq r-1$
. By the induction hypothesis,
![]() $G'$
contains a chordal subgraph
$G'$
contains a chordal subgraph
![]() $H'$
with at least
$H'$
with at least
![]() $r-2$
edges. Now,
$r-2$
edges. Now,
![]() $H' + \{xy\}$
is a chordal subgraph of
$H' + \{xy\}$
is a chordal subgraph of
![]() $G$
with at least
$G$
with at least
![]() $r-1$
edges, as required.
$r-1$
edges, as required.
The rest of this section is dedicated to proving Theorem 1.5. Recall that for
![]() $n \geq 1$
and
$n \geq 1$
and
![]() $m \geq t_2(n) + 1$
, we define
$m \geq t_2(n) + 1$
, we define
![]() $ g_2(n,m) \;:\!=\; \min _{t,r}(2n-t+r),$
where the minimum is taken over all integers
$ g_2(n,m) \;:\!=\; \min _{t,r}(2n-t+r),$
where the minimum is taken over all integers
![]() $t,r \geq 0$
satisfying
$t,r \geq 0$
satisfying
![]() $t(n-t)+t_2(r) \geq m$
. We start by proving the upper bound in Theorem 1.5. First we claim that
$t(n-t)+t_2(r) \geq m$
. We start by proving the upper bound in Theorem 1.5. First we claim that
![]() $g_2(n,m) \leq 2n$
. Indeed, for
$g_2(n,m) \leq 2n$
. Indeed, for
![]() $t = r = \lceil \frac{2n}{3} \rceil$
we have
$t = r = \lceil \frac{2n}{3} \rceil$
we have
![]() $t(n-t) + t_2(r) = t_3(n) \geq m$
, so
$t(n-t) + t_2(r) = t_3(n) \geq m$
, so
![]() $g_2(n,m) \leq 2n - t + r = 2n$
, as required. Now take
$g_2(n,m) \leq 2n - t + r = 2n$
, as required. Now take
![]() $t,r$
such that
$t,r$
such that
![]() $t(n-t) + t_2(r) \geq m$
and
$t(n-t) + t_2(r) \geq m$
and
![]() $g_2(n,m) = 2n-t+r$
. Since
$g_2(n,m) = 2n-t+r$
. Since
![]() $g_2(n,m) \leq 2n$
, we have
$g_2(n,m) \leq 2n$
, we have
![]() $t \geq r$
. Take a complete bipartite graph with sides
$t \geq r$
. Take a complete bipartite graph with sides
![]() $X$
of size
$X$
of size
![]() $t$
and
$t$
and
![]() $Y$
of size
$Y$
of size
![]() $n-t$
and add a copy of
$n-t$
and add a copy of
![]() $T_2(r)$
with sides
$T_2(r)$
with sides
![]() $A,B$
inside
$A,B$
inside
![]() $X$
. The resulting graph
$X$
. The resulting graph
![]() $G$
has
$G$
has
![]() $t(n-t) + t_2(r) \geq m$
edges. Let
$t(n-t) + t_2(r) \geq m$
edges. Let
![]() $H$
be a chordal subgraph of
$H$
be a chordal subgraph of
![]() $G$
. Then
$G$
. Then
![]() $e_H(A,B) \leq |A|+|B|-1 = r-1$
,
$e_H(A,B) \leq |A|+|B|-1 = r-1$
,
![]() $e_H(A,Y) \leq |A|+|Y|-1$
and
$e_H(A,Y) \leq |A|+|Y|-1$
and
![]() $e_H(X\setminus A,Y) \leq |X| - |A| + |Y| - 1$
, because each of these bipartite graphs is induced in
$e_H(X\setminus A,Y) \leq |X| - |A| + |Y| - 1$
, because each of these bipartite graphs is induced in
![]() $G$
, so its intersection with
$G$
, so its intersection with
![]() $H$
is a forest. Overall, we got that
$H$
is a forest. Overall, we got that
![]() $e(H) \leq r-1 + |X| + 2|Y| - 2 = 2n - t + r - 3 = g_2(n,m) - 3$
. This shows that
$e(H) \leq r-1 + |X| + 2|Y| - 2 = 2n - t + r - 3 = g_2(n,m) - 3$
. This shows that
![]() $f(n,m) \leq g_2(n,m)-3$
, as required. To prove the lower bound in Theorem 1.5, we prove the following stronger claim.
$f(n,m) \leq g_2(n,m)-3$
, as required. To prove the lower bound in Theorem 1.5, we prove the following stronger claim.
Theorem 3.1.
Let
![]() $G$
be a graph with
$G$
be a graph with
![]() $n$
vertices and
$n$
vertices and
![]() $m \geq t_2(n)+1$
edges, and let
$m \geq t_2(n)+1$
edges, and let
![]() $x,y,z$
be a triangle in
$x,y,z$
be a triangle in
![]() $G$
. Then
$G$
. Then
![]() $G$
has a chordal subgraph with at least
$G$
has a chordal subgraph with at least
![]() $g_2(n,m)-3$
edges which contains the edges
$g_2(n,m)-3$
edges which contains the edges
![]() $xy,xz,yz$
.
$xy,xz,yz$
.
We need the following facts about the numbers
![]() $g_2(n,m)$
.
$g_2(n,m)$
.
Lemma 3.2.
In the definition of
![]() $g_2(n,m)$
, we may assume that
$g_2(n,m)$
, we may assume that
![]() $-\frac{1}{2} \leq 2t - n - \frac{r}{2} \leq \frac{1}{2}$
.
$-\frac{1}{2} \leq 2t - n - \frac{r}{2} \leq \frac{1}{2}$
.
Proof. Fix
![]() $t,r$
which achieve the minimum in the definition of
$t,r$
which achieve the minimum in the definition of
![]() $g_2(n,m)$
; so
$g_2(n,m)$
; so
![]() $t(n-t)+t_2(r) \geq m$
and
$t(n-t)+t_2(r) \geq m$
and
![]() $g_2(n,m) = 2n-t+r$
. Put
$g_2(n,m) = 2n-t+r$
. Put
![]() $h(t,r) \;:\!=\; 2t - n - \frac{r}{2}$
. If
$h(t,r) \;:\!=\; 2t - n - \frac{r}{2}$
. If
![]() $h(t,r) \in \{-\frac{1}{2},0,\frac{1}{2}\}$
then we are done. If not, we try replacing
$h(t,r) \in \{-\frac{1}{2},0,\frac{1}{2}\}$
then we are done. If not, we try replacing
![]() $(t,r)$
with
$(t,r)$
with
![]() $(t-1,r-1)$
or
$(t-1,r-1)$
or
![]() $(t+1,r+1)$
. Suppose first that
$(t+1,r+1)$
. Suppose first that
![]() $h(t,r) \geq 1$
. Replace
$h(t,r) \geq 1$
. Replace
![]() $(t,r)$
with
$(t,r)$
with
![]() $(t-1,r-1)$
. We have
$(t-1,r-1)$
. We have
![]() $2n - (t-1) + (r-1) = 2n-t+r$
and
$2n - (t-1) + (r-1) = 2n-t+r$
and
![]() $(t-1)(n-t+1) + t_2(r-1) = t(n-t) + t_2(r) - n + 2t - \lfloor \frac{r}{2} \rfloor - 1 \geq t(n-t) + t_2(r) \geq m$
, where the penultimate inequality uses
$(t-1)(n-t+1) + t_2(r-1) = t(n-t) + t_2(r) - n + 2t - \lfloor \frac{r}{2} \rfloor - 1 \geq t(n-t) + t_2(r) \geq m$
, where the penultimate inequality uses
![]() $h(t,r) \geq 1$
. So
$h(t,r) \geq 1$
. So
![]() $(t-1,r-1)$
also achieves the minimum in the definition of
$(t-1,r-1)$
also achieves the minimum in the definition of
![]() $g_2(n,m)$
. Moreover,
$g_2(n,m)$
. Moreover,
![]() $h(t-1,r-1) = 2(t-1) - n - \frac{r-1}{2} = h(t,r) - \frac{3}{2}$
. So as long as
$h(t-1,r-1) = 2(t-1) - n - \frac{r-1}{2} = h(t,r) - \frac{3}{2}$
. So as long as
![]() $h(t,r) \geq 1$
, we can replace
$h(t,r) \geq 1$
, we can replace
![]() $(t,r)$
with
$(t,r)$
with
![]() $(t-1,r-1)$
and decrease
$(t-1,r-1)$
and decrease
![]() $h$
by
$h$
by
![]() $\frac{3}{2}$
. At the last step, we decrease
$\frac{3}{2}$
. At the last step, we decrease
![]() $h$
to be in
$h$
to be in
![]() $\left\{-\frac{1}{2}, 0, \frac{1}{2}\right\}$
.
$\left\{-\frac{1}{2}, 0, \frac{1}{2}\right\}$
.
Similarly, suppose that
![]() $h(t,r) \leq -1$
. Replace
$h(t,r) \leq -1$
. Replace
![]() $(t,r)$
with
$(t,r)$
with
![]() $(t+1,r+1)$
. We have
$(t+1,r+1)$
. We have
![]() $2n-(t+1) + (r+1) = 2n-t+r$
and
$2n-(t+1) + (r+1) = 2n-t+r$
and
![]() $(t+1)(n-t-1) + t_2(r+1) = t(n-t) + t_2(r) + n - 2t + \lceil \frac{r}{2} \rceil - 1 \geq t(n-t) + t_2(r) \geq m$
, where the penultimate inequality uses
$(t+1)(n-t-1) + t_2(r+1) = t(n-t) + t_2(r) + n - 2t + \lceil \frac{r}{2} \rceil - 1 \geq t(n-t) + t_2(r) \geq m$
, where the penultimate inequality uses
![]() $h(t,r) \leq -1$
. So
$h(t,r) \leq -1$
. So
![]() $(t+1,r+1)$
also achieves the minimum in the definition of
$(t+1,r+1)$
also achieves the minimum in the definition of
![]() $g_2(n,m)$
. Also,
$g_2(n,m)$
. Also,
![]() $h(t+1,r+1) = 2(t+1) - n - \frac{r+1}{2} = h(t,r) + \frac{3}{2}$
. So as long as
$h(t+1,r+1) = 2(t+1) - n - \frac{r+1}{2} = h(t,r) + \frac{3}{2}$
. So as long as
![]() $h(t,r) \leq -1$
, we can replace
$h(t,r) \leq -1$
, we can replace
![]() $(t,r)$
with
$(t,r)$
with
![]() $(t+1,r+1)$
and increase
$(t+1,r+1)$
and increase
![]() $h$
by
$h$
by
![]() $\frac{3}{2}$
. At the last step, we increase
$\frac{3}{2}$
. At the last step, we increase
![]() $h$
to be in
$h$
to be in
![]() $\left\{-\frac{1}{2}, 0, \frac{1}{2}\right\}$
.
$\left\{-\frac{1}{2}, 0, \frac{1}{2}\right\}$
.
Lemma 3.3.
For
![]() $n \geq 1$
and
$n \geq 1$
and
![]() $m \geq t_2(n) + 2$
, it holds that
$m \geq t_2(n) + 2$
, it holds that
![]() $g_2(n,m-1) \geq g_2(n,m) - 1$
.
$g_2(n,m-1) \geq g_2(n,m) - 1$
.
Proof. Let
![]() $t,r$
be such that
$t,r$
be such that
![]() $t(n-t) + t_2(r) \geq m-1$
and
$t(n-t) + t_2(r) \geq m-1$
and
![]() $2n-t+r = g_2(n,m-1)$
. Since
$2n-t+r = g_2(n,m-1)$
. Since
![]() $m-1 \geq t_2(n)+1$
we have
$m-1 \geq t_2(n)+1$
we have
![]() $r \geq 2$
. Thus
$r \geq 2$
. Thus
![]() $t(n-t) + t_2(r+1) \geq m$
, so
$t(n-t) + t_2(r+1) \geq m$
, so
![]() $g_2(n,m) \leq 2n-t+(r+1) = g_2(n,m-1) + 1$
, as required.
$g_2(n,m) \leq 2n-t+(r+1) = g_2(n,m-1) + 1$
, as required.
Lemma 3.4.
The following holds for every
![]() $n \geq 3$
.
$n \geq 3$
.
-
1. If
 $m \geq t_2(n) + 1$
then
$m \geq t_2(n) + 1$
then
 $m - n + 1 \geq t_2(n-2) + 1$
and
$m - n + 1 \geq t_2(n-2) + 1$
and
 $g_2(n-2,m-n+1) \geq g_2(n,m) - 3$
.
$g_2(n-2,m-n+1) \geq g_2(n,m) - 3$
. -
2. If
 $m \geq t_2(n) + 2$
then
$m \geq t_2(n) + 2$
then
 $m -n \geq t_2(n-2)+1$
and
$m -n \geq t_2(n-2)+1$
and
 $g_2(n-2,m-n) \geq g_2(n,m) - 4$
.
$g_2(n-2,m-n) \geq g_2(n,m) - 4$
.
Proof. The first part in both items follows from
![]() $t_2(n-2) = t_2(n) - n + 1$
. Let
$t_2(n-2) = t_2(n) - n + 1$
. Let
![]() $t,r$
such that
$t,r$
such that
![]() $t(n-2-t) + t_2(r) \geq m-n+1$
and
$t(n-2-t) + t_2(r) \geq m-n+1$
and
![]() $g_2(n-2,m-n+1) = 2(n-2) - t + r$
. We have
$g_2(n-2,m-n+1) = 2(n-2) - t + r$
. We have
![]() $(t+1) (n-1-t) + t_2(r) = t(n-2-t) + n-1 + t_2(r) \geq m$
. Hence,
$(t+1) (n-1-t) + t_2(r) = t(n-2-t) + n-1 + t_2(r) \geq m$
. Hence,
![]() $g_2(n,m) \leq 2n - (t+1) + r = g_2(n-2,m-n+1) + 3$
. This proves the first item. For the second item,
$g_2(n,m) \leq 2n - (t+1) + r = g_2(n-2,m-n+1) + 3$
. This proves the first item. For the second item,
![]() $g_2(n-2,m-n) \geq g_2(n-2,m-n+1) - 1 \geq g_2(n,m) - 4$
, where the first equality uses Lemma 3.3 since
$g_2(n-2,m-n) \geq g_2(n-2,m-n+1) - 1 \geq g_2(n,m) - 4$
, where the first equality uses Lemma 3.3 since
![]() $m-n+1\geq t_2(n-2)+2$
.
$m-n+1\geq t_2(n-2)+2$
.
Lemma 3.5.
Let
![]() $n \geq 1$
and
$n \geq 1$
and
![]() $m \geq t_2(n) + 1$
, and let
$m \geq t_2(n) + 1$
, and let
![]() $d \geq 0$
be an integer satisfying
$d \geq 0$
be an integer satisfying
![]() $3d \leq g_2(n,m)-1$
. Then
$3d \leq g_2(n,m)-1$
. Then
![]() $m-d \geq t_2(n-1)+1$
and
$m-d \geq t_2(n-1)+1$
and
![]() $g_2(n-1,m-d) \geq g_2(n,m) - 2$
.
$g_2(n-1,m-d) \geq g_2(n,m) - 2$
.
Lemma 3.5 is used in the proof of Theorem 3.1 in case one of the vertices
![]() $x,y,z$
has degree at most
$x,y,z$
has degree at most
![]() $d$
. We then delete this vertex, apply induction and then add the vertex back with its two incident edges on the triangle. The induction carries through thanks to the bound
$d$
. We then delete this vertex, apply induction and then add the vertex back with its two incident edges on the triangle. The induction carries through thanks to the bound
![]() $g_2(n-1, m-d) \geq g_2(n,m) - 2$
from Lemma 3.5. The reason for the assumption
$g_2(n-1, m-d) \geq g_2(n,m) - 2$
from Lemma 3.5. The reason for the assumption
![]() $3d \leq g_2(n,m)-1$
is that if
$3d \leq g_2(n,m)-1$
is that if
![]() $d(x) + d(y) + d(z) \geq g_2(n,m)$
then the graph consisting of all edges touching
$d(x) + d(y) + d(z) \geq g_2(n,m)$
then the graph consisting of all edges touching
![]() $x,y,z$
is a chordal graph with at least
$x,y,z$
is a chordal graph with at least
![]() $g_2(n,m)-3$
edges, as required by Theorem 3.1. So we may always assume that one of
$g_2(n,m)-3$
edges, as required by Theorem 3.1. So we may always assume that one of
![]() $x,y,z$
has degree
$x,y,z$
has degree
![]() $d$
with
$d$
with
![]() $3d \leq g_2(n,m)-1$
.
$3d \leq g_2(n,m)-1$
.
Proof of Lemma
3.5
. First we show that
![]() $m-d \gt t_2(n-1)$
. Set
$m-d \gt t_2(n-1)$
. Set
![]() $a \;:\!=\; m - t_2(n)$
. Since
$a \;:\!=\; m - t_2(n)$
. Since
![]() $3d \leq g_2(n,m) - 1$
, it is enough to show that
$3d \leq g_2(n,m) - 1$
, it is enough to show that
For
![]() $a=1$
,
$a=1$
,
![]() $g_2(n,m) = n + \lfloor \frac{n}{2} \rfloor + 2 \lt 3 \cdot \lfloor \frac{n}{2} \rfloor + 4$
, and the last expression equals the right-hand side of (7). Suppose now that
$g_2(n,m) = n + \lfloor \frac{n}{2} \rfloor + 2 \lt 3 \cdot \lfloor \frac{n}{2} \rfloor + 4$
, and the last expression equals the right-hand side of (7). Suppose now that
![]() $a \geq 2$
. Set
$a \geq 2$
. Set
![]() $k = \lceil \sqrt{\frac{a}{3}} \rceil$
, so that
$k = \lceil \sqrt{\frac{a}{3}} \rceil$
, so that
![]() $3k^2 \geq a$
. Set
$3k^2 \geq a$
. Set
![]() $t \;:\!=\; \lfloor \frac{n}{2} \rfloor + k$
and
$t \;:\!=\; \lfloor \frac{n}{2} \rfloor + k$
and
![]() $r \;:\!=\; 4k$
. Then
$r \;:\!=\; 4k$
. Then
![]() $t_2(r) = 4k^2$
and
$t_2(r) = 4k^2$
and
so
![]() $t(n-t) + t_2(r) \geq t_2(n) + 3k^2 \geq t_2(n) + a = m$
. Hence,
$t(n-t) + t_2(r) \geq t_2(n) + 3k^2 \geq t_2(n) + a = m$
. Hence,
![]() $g_2(n,m) \leq 2n - t + r = 2n - \lfloor \frac{n}{2} \rfloor + 3k \leq 3 \cdot \lfloor \frac{n}{2} \rfloor + 2 + 3k$
. So to prove (7), it suffices to show that
$g_2(n,m) \leq 2n - t + r = 2n - \lfloor \frac{n}{2} \rfloor + 3k \leq 3 \cdot \lfloor \frac{n}{2} \rfloor + 2 + 3k$
. So to prove (7), it suffices to show that
![]() $3k+1 \lt 3a$
. As
$3k+1 \lt 3a$
. As
![]() $k \leq \sqrt{\frac{a}{3}}+1$
, it suffices to show that
$k \leq \sqrt{\frac{a}{3}}+1$
, it suffices to show that
![]() $3\left ( \sqrt{\frac{a}{3}}+1 \right ) \lt 3a-1$
. Rearranging and squaring, we get the inequality
$3\left ( \sqrt{\frac{a}{3}}+1 \right ) \lt 3a-1$
. Rearranging and squaring, we get the inequality
![]() $9a^2-27a+16 \gt 0$
, which holds for all
$9a^2-27a+16 \gt 0$
, which holds for all
![]() $a \geq 3$
. For
$a \geq 3$
. For
![]() $a=2$
we simply note that
$a=2$
we simply note that
![]() $k = 1$
and so
$k = 1$
and so
![]() $3k+1 = 4 \lt 6 = 3a$
.
$3k+1 = 4 \lt 6 = 3a$
.
Now we show that
![]() $g_2(n-1,m-d) \geq g(n,m) - 2$
. Fix
$g_2(n-1,m-d) \geq g(n,m) - 2$
. Fix
![]() $t,r$
that achieve the minimum in the definition of
$t,r$
that achieve the minimum in the definition of
![]() $g_2(n,m)$
; so
$g_2(n,m)$
; so
![]() $t(n-t)+t_2(r) \geq m$
and
$t(n-t)+t_2(r) \geq m$
and
By Lemma 3.2, we may assume that
![]() $-\frac{1}{2} \leq 2t-n-\frac{r}{2} \leq \frac{1}{2}.$
Fix also
$-\frac{1}{2} \leq 2t-n-\frac{r}{2} \leq \frac{1}{2}.$
Fix also
![]() $t',r'$
such that
$t',r'$
such that
![]() $t'(n-1-t') + t_2(r') \geq m-d$
and
$t'(n-1-t') + t_2(r') \geq m-d$
and
![]() $g_2(n-1,m-d) = 2(n-1) - t' + r'$
. Suppose by contradiction that
$g_2(n-1,m-d) = 2(n-1) - t' + r'$
. Suppose by contradiction that
![]() $g_2(n-1, m-d) \leq g_2(n,m)-3$
. Then
$g_2(n-1, m-d) \leq g_2(n,m)-3$
. Then
![]() $2(n-1) - t' + r' \leq 2n - t + r - 3$
, so
$2(n-1) - t' + r' \leq 2n - t + r - 3$
, so
![]() $t' - t \geq r' - r + 1$
. Put
$t' - t \geq r' - r + 1$
. Put
![]() $c \;:\!=\; t'-t$
, so that
$c \;:\!=\; t'-t$
, so that
![]() $r' \leq r+c-1$
. Then
$r' \leq r+c-1$
. Then
![]() $t_2(r') \leq t_2(r+c-1)$
. So we can write
$t_2(r') \leq t_2(r+c-1)$
. So we can write
 \begin{equation} \begin{split} m-d &\leq t'(n-1-t') + t_2(r') \leq (t+c)(n-t-c-1) + t_2(r+c-1) \\[5pt] &= t(n-t) + cn - (2c+1)t - (c+1)c + t_2(r+c-1). \end{split} \end{equation}
\begin{equation} \begin{split} m-d &\leq t'(n-1-t') + t_2(r') \leq (t+c)(n-t-c-1) + t_2(r+c-1) \\[5pt] &= t(n-t) + cn - (2c+1)t - (c+1)c + t_2(r+c-1). \end{split} \end{equation}
Since
![]() $(t,r)$
achieves the minimum in the definition of
$(t,r)$
achieves the minimum in the definition of
![]() $g_2(n,m)$
, we must have
$g_2(n,m)$
, we must have
![]() $m-1 \geq t(n-t) + t_2(r-1)$
, so
$m-1 \geq t(n-t) + t_2(r-1)$
, so
![]() $t(n-t) \leq m-1-t_2(r-1)$
. Plugging this into (9) and rearranging, we get
$t(n-t) \leq m-1-t_2(r-1)$
. Plugging this into (9) and rearranging, we get
Note that
So we get
We now complete the proof by considering the three possible values of
![]() $2t-n-\frac{r}{2}$
. Suppose first that
$2t-n-\frac{r}{2}$
. Suppose first that
![]() $2t-n-\frac{r}{2} = 0$
. Then
$2t-n-\frac{r}{2} = 0$
. Then
![]() $g_2(n,m) = 3t$
by (8). By (10), we have
$g_2(n,m) = 3t$
by (8). By (10), we have
![]() $d \geq t + (c+1)c + 1 - \frac{(c-1)^2}{4} = t + \frac{3}{4}(c+1)^2 \geq t = g_2(n,m)/3$
, in contradiction to our assumption on
$d \geq t + (c+1)c + 1 - \frac{(c-1)^2}{4} = t + \frac{3}{4}(c+1)^2 \geq t = g_2(n,m)/3$
, in contradiction to our assumption on
![]() $d$
.
$d$
.
Suppose now that
![]() $2t-n - \frac{r}{2} = \frac{1}{2}$
. Then
$2t-n - \frac{r}{2} = \frac{1}{2}$
. Then
![]() $g_2(n,m) = 3t-1$
by (8). By (10), we have
$g_2(n,m) = 3t-1$
by (8). By (10), we have
![]() $d \geq t + \frac{c}{2} + (c+ 1)c + 1 - \frac{c^2-2c+1}{4} = t+\frac{3c^2}{4} + 2c+\frac{3}{4} \gt t-1$
, where the last inequality holds for every
$d \geq t + \frac{c}{2} + (c+ 1)c + 1 - \frac{c^2-2c+1}{4} = t+\frac{3c^2}{4} + 2c+\frac{3}{4} \gt t-1$
, where the last inequality holds for every
![]() $c$
. So
$c$
. So
![]() $d \geq t$
and hence
$d \geq t$
and hence
![]() $3d \geq 3t \geq g_2(n,m)$
, a contradiction.
$3d \geq 3t \geq g_2(n,m)$
, a contradiction.
Finally, suppose that
![]() $2t-n - \frac{r}{2} = -\frac{1}{2}$
. Then
$2t-n - \frac{r}{2} = -\frac{1}{2}$
. Then
![]() $g_2(n,m) = 3t+1$
by (8). By (10), we have
$g_2(n,m) = 3t+1$
by (8). By (10), we have
![]() $d \geq t - \frac{c}{2} + (c+ 1)c + 1 - \frac{c^2-2c+1}{4} = t+\frac{3c^2}{4} + c + \frac{3}{4} \gt t$
, where the last inequality holds for every
$d \geq t - \frac{c}{2} + (c+ 1)c + 1 - \frac{c^2-2c+1}{4} = t+\frac{3c^2}{4} + c + \frac{3}{4} \gt t$
, where the last inequality holds for every
![]() $c$
. So
$c$
. So
![]() $d \geq t+1$
and hence
$d \geq t+1$
and hence
![]() $3d \geq 3t+3 \geq g_2(n,m)$
, a contradiction.
$3d \geq 3t+3 \geq g_2(n,m)$
, a contradiction.
Proof of Theorem
3.1
. The proof is by induction on
![]() $n$
. The base cases
$n$
. The base cases
![]() $n=1,2$
are trivial because for these
$n=1,2$
are trivial because for these
![]() $n$
there is no graph on
$n$
there is no graph on
![]() $n$
vertices with
$n$
vertices with
![]() $t_2(n)+1$
edges. The case
$t_2(n)+1$
edges. The case
![]() $n = 3$
is also easy to verify. So from now on let
$n = 3$
is also easy to verify. So from now on let
![]() $n \geq 4$
. Let
$n \geq 4$
. Let
![]() $x,y,z$
be a triangle in
$x,y,z$
be a triangle in
![]() $G$
. We consider several cases. After dealing with each case, we will assume in all subsequent cases that this case does not hold.
$G$
. We consider several cases. After dealing with each case, we will assume in all subsequent cases that this case does not hold.
Case 1:
![]() $d(x) + d(y) + d(z) \geq g_2(n,m)$
. In this case, take
$d(x) + d(y) + d(z) \geq g_2(n,m)$
. In this case, take
![]() $H$
to be the graph consisting of all edges touching
$H$
to be the graph consisting of all edges touching
![]() $x,y,z$
. This graph is chordal and clearly contains the edges of the triangle
$x,y,z$
. This graph is chordal and clearly contains the edges of the triangle
![]() $x,y,z$
. Also,
$x,y,z$
. Also,
![]() $e(H) = d(x) + d(y) + d(z) - 3 \geq g_2(n,m) - 3$
, as required.
$e(H) = d(x) + d(y) + d(z) - 3 \geq g_2(n,m) - 3$
, as required.
Case 2: There are distinct
![]() $u,v \in \{x,y,z\}$
such that
$u,v \in \{x,y,z\}$
such that
![]() $d(u) + d(v) \leq n$
. Without loss of generality, suppose that
$d(u) + d(v) \leq n$
. Without loss of generality, suppose that
![]() $u = x, v = y$
. Let
$u = x, v = y$
. Let
![]() $G' = G - \{x,y\}$
. Then
$G' = G - \{x,y\}$
. Then
![]() $ e(G') = e(G) - d(x) - d(y) + 1 \geq m - n + 1$
. By the induction hypothesis (applied to any arbitrary triangle in
$ e(G') = e(G) - d(x) - d(y) + 1 \geq m - n + 1$
. By the induction hypothesis (applied to any arbitrary triangle in
![]() $G'$
),
$G'$
),
![]() $G'$
contains a chordal subgraph
$G'$
contains a chordal subgraph
![]() $H'$
with
$H'$
with
![]() $e(H') \geq g_2(n-2, m-n+1) - 3 \geq g_2(n,m) - 6$
, by Lemma 3.4. Let
$e(H') \geq g_2(n-2, m-n+1) - 3 \geq g_2(n,m) - 6$
, by Lemma 3.4. Let
![]() $H \;:\!=\; H' + \{xy,xz,yz\}$
. Then
$H \;:\!=\; H' + \{xy,xz,yz\}$
. Then
![]() $H$
is chordal, contains the edges of the triangle
$H$
is chordal, contains the edges of the triangle
![]() $x,y,z$
, and satisfies
$x,y,z$
, and satisfies
![]() $e(H) = e(H') + 3 \geq g_2(n,m) - 3$
.
$e(H) = e(H') + 3 \geq g_2(n,m) - 3$
.
We claim that if cases - do not hold then
![]() $m \geq t_2(n)+2$
. Indeed, suppose by contradiction that
$m \geq t_2(n)+2$
. Indeed, suppose by contradiction that
![]() $m = t_2(n)+1$
. We have
$m = t_2(n)+1$
. We have
![]() $g_2(n,t_2(n)+1) = 2n - \lceil \frac{n}{2} \rceil + 2$
. Since case does not hold,
$g_2(n,t_2(n)+1) = 2n - \lceil \frac{n}{2} \rceil + 2$
. Since case does not hold,
![]() $d(x) + d(y) + d(z) \leq g_2(n,t_2(n)+1) - 1 \leq \frac{3n}{2} + 1$
. But then there are distinct
$d(x) + d(y) + d(z) \leq g_2(n,t_2(n)+1) - 1 \leq \frac{3n}{2} + 1$
. But then there are distinct
![]() $u,v \in \{x,y,z\}$
with
$u,v \in \{x,y,z\}$
with
![]() $d(u) + d(v) \leq \frac{2}{3} \cdot \left ( \frac{3n}{2} + 1 \right ) \leq n + \frac{2}{3}$
. Hence
$d(u) + d(v) \leq \frac{2}{3} \cdot \left ( \frac{3n}{2} + 1 \right ) \leq n + \frac{2}{3}$
. Hence
![]() $d(u) + d(v) \leq n$
, contradicting that case does not hold. So
$d(u) + d(v) \leq n$
, contradicting that case does not hold. So
![]() $m \geq t_2(n)+2$
.
$m \geq t_2(n)+2$
.
Case 3: There are distinct
![]() $u,v \in \{x,y,z\}$
such that the edge
$u,v \in \{x,y,z\}$
such that the edge
![]() $uv$
is on exactly one triangle (namely the triangle
$uv$
is on exactly one triangle (namely the triangle
![]() $x,y,z$
). Without loss of generality, suppose that
$x,y,z$
). Without loss of generality, suppose that
![]() $u = x, v = y$
. Since case does not hold, we have
$u = x, v = y$
. Since case does not hold, we have
![]() $d(x) + d(y) \geq n+1$
. On the other hand, since
$d(x) + d(y) \geq n+1$
. On the other hand, since
![]() $xy$
is on exactly one triangle, it must be that
$xy$
is on exactly one triangle, it must be that
![]() $d(x) + d(y) = n+1$
,
$d(x) + d(y) = n+1$
,
![]() $N(x) \cap N(y) = \{z\}$
and every vertex in
$N(x) \cap N(y) = \{z\}$
and every vertex in
![]() $V(G) \setminus \{x,y,z\}$
is adjacent to exactly one of
$V(G) \setminus \{x,y,z\}$
is adjacent to exactly one of
![]() $x,y$
. Let
$x,y$
. Let
![]() $G' = G - \{x,y\}$
. Then
$G' = G - \{x,y\}$
. Then
![]() $e(G') = e(G) - d(x) - d(y) + 1 = m - n$
. By Lemma 3.4,
$e(G') = e(G) - d(x) - d(y) + 1 = m - n$
. By Lemma 3.4,
![]() $e(G') \geq t_2(v(G')) + 1$
, which means that
$e(G') \geq t_2(v(G')) + 1$
, which means that
![]() $G'$
contains a triangle. By the induction hypothesis (applied to an arbitrary triangle in
$G'$
contains a triangle. By the induction hypothesis (applied to an arbitrary triangle in
![]() $G'$
),
$G'$
),
![]() $G'$
contains a chordal subgraph
$G'$
contains a chordal subgraph
![]() $H'$
with
$H'$
with
![]() $ e(H') \geq g_2(n-2, m-n) - 3 \geq g_2(n,m) - 7$
, by Lemma 3.4. So it is enough to show that
$ e(H') \geq g_2(n-2, m-n) - 3 \geq g_2(n,m) - 7$
, by Lemma 3.4. So it is enough to show that
![]() $G$
contains a chordal graph
$G$
contains a chordal graph
![]() $H$
which contains the edges of the triangle
$H$
which contains the edges of the triangle
![]() $x,y,z$
and satisfies
$x,y,z$
and satisfies
![]() $e(H) = e(H') + 4$
. Suppose first that
$e(H) = e(H') + 4$
. Suppose first that
![]() $z$
is isolated in
$z$
is isolated in
![]() $H'$
. We claim that there exists
$H'$
. We claim that there exists
![]() $w \in N_G(z) \setminus \{x,y\}$
. Indeed, if not, then
$w \in N_G(z) \setminus \{x,y\}$
. Indeed, if not, then
![]() $d_G(z) = 2$
. Also, as
$d_G(z) = 2$
. Also, as
![]() $d(x) + d(y) = n+1$
, we have
$d(x) + d(y) = n+1$
, we have
![]() $d(x) \leq \lfloor \frac{n+1}{2} \rfloor$
or
$d(x) \leq \lfloor \frac{n+1}{2} \rfloor$
or
![]() $d(y) \leq \lfloor \frac{n+1}{2} \rfloor$
. Suppose this holds for
$d(y) \leq \lfloor \frac{n+1}{2} \rfloor$
. Suppose this holds for
![]() $y$
. Then
$y$
. Then
![]() $d(y) + d(z) \leq \lfloor \frac{n+1}{2} \rfloor + 2 \leq n$
for
$d(y) + d(z) \leq \lfloor \frac{n+1}{2} \rfloor + 2 \leq n$
for
![]() $n \geq 4$
, so case holds, contradiction. This proves our claim that there exists
$n \geq 4$
, so case holds, contradiction. This proves our claim that there exists
![]() $w \in N_G(z) \setminus \{x,y\}$
. Now take
$w \in N_G(z) \setminus \{x,y\}$
. Now take
![]() $H = H' + \{zw,xy,xz,yz\}$
. By adding the vertices in the order
$H = H' + \{zw,xy,xz,yz\}$
. By adding the vertices in the order
![]() $z,x,y$
, we always add a simplicial vertex. Hence,
$z,x,y$
, we always add a simplicial vertex. Hence,
![]() $H$
is chordal.
$H$
is chordal.
Suppose now that
![]() $z$
is not isolated in
$z$
is not isolated in
![]() $H'$
, and let
$H'$
, and let
![]() $w \in V(G) \setminus \{x,y,z\}$
such that
$w \in V(G) \setminus \{x,y,z\}$
such that
![]() $zw \in E(H')$
. As mentioned above,
$zw \in E(H')$
. As mentioned above,
![]() $w$
is adjacent in
$w$
is adjacent in
![]() $G$
to either
$G$
to either
![]() $x$
or
$x$
or
![]() $y$
; without loss of generality it is adjacent to
$y$
; without loss of generality it is adjacent to
![]() $x$
. Take
$x$
. Take
![]() $H = H' + \{xw,xy,xz,yz\}$
. By adding to
$H = H' + \{xw,xy,xz,yz\}$
. By adding to
![]() $H'$
first
$H'$
first
![]() $x$
and then
$x$
and then
![]() $y$
, we always add a simplicial vertex. Hence,
$y$
, we always add a simplicial vertex. Hence,
![]() $H$
is chordal.
$H$
is chordal.
Case 4: Cases - do not hold. Since case does not hold, we have
![]() $d(x) + d(y) + d(z) \leq g_2(n,m) - 1$
. Assume that
$d(x) + d(y) + d(z) \leq g_2(n,m) - 1$
. Assume that
![]() $d \;:\!=\; d(x) \leq d(y) \leq d(z)$
; then
$d \;:\!=\; d(x) \leq d(y) \leq d(z)$
; then
![]() $3d \leq g_2(n,m) - 1$
. Since case does not hold, there exists
$3d \leq g_2(n,m) - 1$
. Since case does not hold, there exists
![]() $w \in V(G) \setminus \{x\}$
which is a common neighbour of
$w \in V(G) \setminus \{x\}$
which is a common neighbour of
![]() $y,z$
. Set
$y,z$
. Set
![]() $G' = G - \{x\}$
. We have
$G' = G - \{x\}$
. We have
![]() $e(G') = m - d$
. By the induction hypothesis,
$e(G') = m - d$
. By the induction hypothesis,
![]() $G'$
has a chordal subgraph
$G'$
has a chordal subgraph
![]() $H'$
which contains the edges of the triangle
$H'$
which contains the edges of the triangle
![]() $y,z,w$
and satisfies
$y,z,w$
and satisfies
![]() $ e(H') \geq g_2(n-1,m-d) - 3 \geq g_2(n,m) - 5,$
by Lemma 3.5. Let
$ e(H') \geq g_2(n-1,m-d) - 3 \geq g_2(n,m) - 5,$
by Lemma 3.5. Let
![]() $H = H' + \{xy,xz\}$
. Then
$H = H' + \{xy,xz\}$
. Then
![]() $H$
is chordal, contains the edges of the triangle
$H$
is chordal, contains the edges of the triangle
![]() $x,y,z$
, and satisfies
$x,y,z$
, and satisfies
![]() $e(H) = e(H') + 2 \geq g_2(n,m) - 3$
, as required.
$e(H) = e(H') + 2 \geq g_2(n,m) - 3$
, as required.
4. Proof of Theorem 1.2
For convenience, put
![]() $g_3(n) \;:\!=\; 3n-\lceil \frac{n}{3} \rceil +2$
. We prove Theorem 1.2 in the following stronger form.
$g_3(n) \;:\!=\; 3n-\lceil \frac{n}{3} \rceil +2$
. We prove Theorem 1.2 in the following stronger form.
Theorem 4.1.
Let
![]() $G$
be a graph with
$G$
be a graph with
![]() $n$
vertices and
$n$
vertices and
![]() $t_3(n)+1$
edges, and let
$t_3(n)+1$
edges, and let
![]() $X = \{x_1,x_2,x_3,x_4\}$
be a
$X = \{x_1,x_2,x_3,x_4\}$
be a
![]() $4$
-clique in
$4$
-clique in
![]() $G$
. Then
$G$
. Then
![]() $G$
has a chordal subgraph with at least
$G$
has a chordal subgraph with at least
![]() $g_3(n) - 6$
edges which contains the edges of the clique
$g_3(n) - 6$
edges which contains the edges of the clique
![]() $X$
.
$X$
.
We need some simple facts on the numbers
![]() $t_3(n)$
and
$t_3(n)$
and
![]() $g_3(n)$
.
$g_3(n)$
.
Lemma 4.2.
For every
![]() $n \geq 5$
, it holds that
$n \geq 5$
, it holds that
![]() $t_3(n) - t_3(n-1) = \lfloor \frac{2n}{3} \rfloor$
,
$t_3(n) - t_3(n-1) = \lfloor \frac{2n}{3} \rfloor$
,
![]() $t_3(n) - t_3(n-2) = \lfloor \frac{4n}{3} \rfloor - 1$
,
$t_3(n) - t_3(n-2) = \lfloor \frac{4n}{3} \rfloor - 1$
,
![]() $t_3(n) - t_3(n-3) = 2n-3$
,
$t_3(n) - t_3(n-3) = 2n-3$
,
![]() $t_3(n) - t_3(n-4) = g_3(n) - 7$
.
$t_3(n) - t_3(n-4) = g_3(n) - 7$
.
Proof. For
![]() $i = 1,2,3$
,
$i = 1,2,3$
,
![]() $T_3(n-i)$
is obtained from
$T_3(n-i)$
is obtained from
![]() $T_3(n)$
by deleting one vertex from each of the
$T_3(n)$
by deleting one vertex from each of the
![]() $i$
largest classes of
$i$
largest classes of
![]() $T_3(n)$
. For
$T_3(n)$
. For
![]() $i = 1$
, the deleted vertex has degree
$i = 1$
, the deleted vertex has degree
![]() $\lfloor \frac{2n}{3} \rfloor$
. For
$\lfloor \frac{2n}{3} \rfloor$
. For
![]() $i = 2$
, the sum of degrees of the deleted vertices is
$i = 2$
, the sum of degrees of the deleted vertices is
![]() $\lfloor \frac{4n}{3} \rfloor$
, and these vertices are adjacent. For
$\lfloor \frac{4n}{3} \rfloor$
, and these vertices are adjacent. For
![]() $i = 3$
, the sum of degrees of the deleted vertices is
$i = 3$
, the sum of degrees of the deleted vertices is
![]() $2n$
, and they form a triangle. Finally,
$2n$
, and they form a triangle. Finally,
![]() $t_3(n) - t_3(n-4) = t_3(n) - t_3(n-1) + t_3(n-1) - t_3(n-4) = \lfloor \frac{2n}{3} \rfloor + 2(n-1)-3 = 3n-\lceil \frac{n}{3} \rceil - 5 = g_3(n) - 7$
.
$t_3(n) - t_3(n-4) = t_3(n) - t_3(n-1) + t_3(n-1) - t_3(n-4) = \lfloor \frac{2n}{3} \rfloor + 2(n-1)-3 = 3n-\lceil \frac{n}{3} \rceil - 5 = g_3(n) - 7$
.
Lemma 4.3.
For every
![]() $n \geq 5$
, it holds that
$n \geq 5$
, it holds that
![]() $g_3(n) - g_3(n-1) = 3$
if
$g_3(n) - g_3(n-1) = 3$
if
![]() $n \equiv 0,2 \pmod{3}$
and
$n \equiv 0,2 \pmod{3}$
and
![]() $g_3(n) - g_3(n-1) = 2$
if
$g_3(n) - g_3(n-1) = 2$
if
![]() $n \equiv 1 \pmod{3}$
. Hence,
$n \equiv 1 \pmod{3}$
. Hence,
![]() $g_3(n) - g_3(n-2) \leq 6$
,
$g_3(n) - g_3(n-2) \leq 6$
,
![]() $g_3(n) - g_3(n-3) = 8$
and
$g_3(n) - g_3(n-3) = 8$
and
![]() $g_3(n) - g_3(n-4) \leq 11$
.
$g_3(n) - g_3(n-4) \leq 11$
.
Proof.
![]() $g_3(n) - g_3(n-1) = 3 - \lceil \frac{n}{3} \rceil + \lceil \frac{n-1}{3} \rceil$
, and it is easy to see that
$g_3(n) - g_3(n-1) = 3 - \lceil \frac{n}{3} \rceil + \lceil \frac{n-1}{3} \rceil$
, and it is easy to see that
![]() $\lceil \frac{n}{3} \rceil - \lceil \frac{n-1}{3} \rceil$
equals
$\lceil \frac{n}{3} \rceil - \lceil \frac{n-1}{3} \rceil$
equals
![]() $0$
if
$0$
if
![]() $n \equiv 0,2 \pmod{3}$
and equals
$n \equiv 0,2 \pmod{3}$
and equals
![]() $1$
if
$1$
if
![]() $n \equiv 1 \pmod{3}$
.
$n \equiv 1 \pmod{3}$
.
We also need the following simple lemma saying that in a graph with
![]() $t_3(n)+1$
edges, we can find two
$t_3(n)+1$
edges, we can find two
![]() $4$
-cliques sharing 3 vertices. This fact is originally due to Dirac [Reference Dirac2]. For completeness, we include a proof.
$4$
-cliques sharing 3 vertices. This fact is originally due to Dirac [Reference Dirac2]. For completeness, we include a proof.
Lemma 4.4.
A graph
![]() $G$
with
$G$
with
![]() $n \geq 5$
vertices and
$n \geq 5$
vertices and
![]() $t_3(n) + 1$
edges has two
$t_3(n) + 1$
edges has two
![]() $4$
-cliques sharing 3 vertices.
$4$
-cliques sharing 3 vertices.
Proof. The proof is by induction on
![]() $n$
. For the base case
$n$
. For the base case
![]() $n = 5$
, take a
$n = 5$
, take a
![]() $4$
-clique and notice that the remaining vertex must send at least 3 edges to this
$4$
-clique and notice that the remaining vertex must send at least 3 edges to this
![]() $4$
-clique as
$4$
-clique as
![]() $t_3(5)+1 = 9$
. Let
$t_3(5)+1 = 9$
. Let
![]() $n \geq 6$
. Take a
$n \geq 6$
. Take a
![]() $4$
-clique
$4$
-clique
![]() $x_1,\dots,x_4$
. If there is a vertex outside of
$x_1,\dots,x_4$
. If there is a vertex outside of
![]() $x_1,\dots,x_4$
which has three neighbours in
$x_1,\dots,x_4$
which has three neighbours in
![]() $x_1,\dots,x_4$
then we are done. Else,
$x_1,\dots,x_4$
then we are done. Else,
![]() $d(x_1) + \dots + d(x_4) \leq 2n+4$
, so there is
$d(x_1) + \dots + d(x_4) \leq 2n+4$
, so there is
![]() $i \in [4]$
such that
$i \in [4]$
such that
![]() $d(x_i) \leq \lfloor \frac{n}{2}\rfloor + 1 \leq \lfloor \frac{2n}{3}\rfloor$
, where the last inequality holds for all
$d(x_i) \leq \lfloor \frac{n}{2}\rfloor + 1 \leq \lfloor \frac{2n}{3}\rfloor$
, where the last inequality holds for all
![]() $n \geq 6$
. So
$n \geq 6$
. So
![]() $G' \;:\!=\; G-x_i$
has at least
$G' \;:\!=\; G-x_i$
has at least
![]() $t_3(n-1)+1$
edges, and we can apply induction.
$t_3(n-1)+1$
edges, and we can apply induction.
Proof of Theorem
4.1
. The proof is by induction on
![]() $n$
. The claim is trivial if
$n$
. The claim is trivial if
![]() $n \leq 4$
so suppose that
$n \leq 4$
so suppose that
![]() $n \geq 5$
. We proceed by a sequence of claims.
$n \geq 5$
. We proceed by a sequence of claims.
Claim 4.5.
We may assume that there exists
![]() $y \in V(G) \setminus \{x_1,\dots,x_4\}$
which is adjacent to at least 3 of the vertices
$y \in V(G) \setminus \{x_1,\dots,x_4\}$
which is adjacent to at least 3 of the vertices
![]() $x_1,\dots,x_4$
.
$x_1,\dots,x_4$
.
Proof of Claim
4.5
. Suppose that there is no such
![]() $y$
. We will show that the assertion of Theorem 4.1 holds. For
$y$
. We will show that the assertion of Theorem 4.1 holds. For
![]() $0 \leq j \leq 2$
, let
$0 \leq j \leq 2$
, let
![]() $A_j$
be the set of vertices in
$A_j$
be the set of vertices in
![]() $V(G) \setminus \{x_1,\dots,x_4\}$
which are adjacent to
$V(G) \setminus \{x_1,\dots,x_4\}$
which are adjacent to
![]() $j$
of the vertices
$j$
of the vertices
![]() $x_1,\dots,x_4$
, and let
$x_1,\dots,x_4$
, and let
![]() $a_j = |A_j|$
. Then
$a_j = |A_j|$
. Then
![]() $a_0 + a_1 + a_2 = n-4$
and
$a_0 + a_1 + a_2 = n-4$
and
![]() $a_1 + 2a_2 = d(x_1) + \dots + d(x_4) - 12$
. So
$a_1 + 2a_2 = d(x_1) + \dots + d(x_4) - 12$
. So
We consider three cases:
Case 1:
![]() $0 \lt a_2 \leq n-5$
. Then
$0 \lt a_2 \leq n-5$
. Then
![]() $d(x_1) + \dots + d(x_4) \leq 2n+3$
by (11). Let
$d(x_1) + \dots + d(x_4) \leq 2n+3$
by (11). Let
![]() $G'$
be the graph obtained from
$G'$
be the graph obtained from
![]() $G$
by deleting
$G$
by deleting
![]() $x_2,x_3,x_4$
and all edges touching
$x_2,x_3,x_4$
and all edges touching
![]() $x_1$
. Then
$x_1$
. Then
![]() $v(G') = n-3$
and
$v(G') = n-3$
and
![]() $e(G') = e(G) - (d(x_1) + \dots + d(x_4)) + 6 \geq e(G) - 2n + 3 = t_3(n) + 1 - 2n + 3 = t_3(n-3) + 1.$
In particular,
$e(G') = e(G) - (d(x_1) + \dots + d(x_4)) + 6 \geq e(G) - 2n + 3 = t_3(n) + 1 - 2n + 3 = t_3(n-3) + 1.$
In particular,
![]() $n-3 \geq 4$
(else
$n-3 \geq 4$
(else
![]() $G'$
cannot have more than
$G'$
cannot have more than
![]() $t_3(n-3)$
edges). By the induction hypothesis (applied to an arbitrary
$t_3(n-3)$
edges). By the induction hypothesis (applied to an arbitrary
![]() $4$
-clique in
$4$
-clique in
![]() $G'$
),
$G'$
),
![]() $G'$
contains a chordal subgraph
$G'$
contains a chordal subgraph
![]() $H'$
with
$H'$
with
![]() $e(H') \geq g_3(n-3)-6$
. Take
$e(H') \geq g_3(n-3)-6$
. Take
![]() $z \in A_2$
and assume without loss of generality that
$z \in A_2$
and assume without loss of generality that
![]() $z$
is adjacent to
$z$
is adjacent to
![]() $x_1,x_2$
. Let
$x_1,x_2$
. Let
![]() $H = H' + \{x_1z,x_2z\} + \{x_ix_j \;:\; 1 \leq i \lt j \leq 4\}$
. Then
$H = H' + \{x_1z,x_2z\} + \{x_ix_j \;:\; 1 \leq i \lt j \leq 4\}$
. Then
![]() $e(H) = e(H') + 8 \geq g_3(n-3) + 8 - 6 = g_3(n) - 6$
. Also,
$e(H) = e(H') + 8 \geq g_3(n-3) + 8 - 6 = g_3(n) - 6$
. Also,
![]() $H$
is chordal: adding
$H$
is chordal: adding
![]() $x_1z$
to
$x_1z$
to
![]() $H'$
keeps it chordal because
$H'$
keeps it chordal because
![]() $x_1$
is isolated in
$x_1$
is isolated in
![]() $H'$
, and then by adding
$H'$
, and then by adding
![]() $x_2,x_3,x_4$
in this order we always add a simplicial vertex.
$x_2,x_3,x_4$
in this order we always add a simplicial vertex.
Case 2:
![]() $a_2 = n-4$
. Then every vertex outside of
$a_2 = n-4$
. Then every vertex outside of
![]() $\{x_1,\dots,x_4\}$
is adjacent to two of the vertices
$\{x_1,\dots,x_4\}$
is adjacent to two of the vertices
![]() $x_1,\dots,x_4$
. By (11),
$x_1,\dots,x_4$
. By (11),
![]() $d(x_1) + \dots + d(x_4) = 2n+4$
. Pick an arbitrary
$d(x_1) + \dots + d(x_4) = 2n+4$
. Pick an arbitrary
![]() $v \in V(G) \setminus \{x_1,\dots,x_4\}$
and suppose without loss of generality that
$v \in V(G) \setminus \{x_1,\dots,x_4\}$
and suppose without loss of generality that
![]() $v$
is adjacent to
$v$
is adjacent to
![]() $x_1$
. Let
$x_1$
. Let
![]() $G'$
be the graph obtained from
$G'$
be the graph obtained from
![]() $G$
by deleting
$G$
by deleting
![]() $x_2,x_3,x_4$
and all edges touching
$x_2,x_3,x_4$
and all edges touching
![]() $x_1$
except for
$x_1$
except for
![]() $x_1v$
. Then
$x_1v$
. Then
![]() $v(G') = n-3$
and
$v(G') = n-3$
and
![]() $e(G') = e(G) - (d(x_1) + \dots + d(x_4)) + 7 = e(G) - 2n + 3 = t_3(n-3) + 1$
. Pick an arbitrary
$e(G') = e(G) - (d(x_1) + \dots + d(x_4)) + 7 = e(G) - 2n + 3 = t_3(n-3) + 1$
. Pick an arbitrary
![]() $4$
-clique
$4$
-clique
![]() $y_1,\dots,y_4$
in
$y_1,\dots,y_4$
in
![]() $G'$
. By the induction hypothesis,
$G'$
. By the induction hypothesis,
![]() $G'$
contains a chordal subgraph
$G'$
contains a chordal subgraph
![]() $H'$
with
$H'$
with
![]() $e(H') \geq g_3(n-3) - 6$
such that
$e(H') \geq g_3(n-3) - 6$
such that
![]() $H'$
contains the edges of the clique
$H'$
contains the edges of the clique
![]() $y_1,\dots,y_4$
. Each
$y_1,\dots,y_4$
. Each
![]() $y_i$
has two neighbours in
$y_i$
has two neighbours in
![]() $x_1,\dots,x_4$
. By pigeonhole, two of the
$x_1,\dots,x_4$
. By pigeonhole, two of the
![]() $y_i$
’s have a common neighbour. Without loss of generality, we may assume that
$y_i$
’s have a common neighbour. Without loss of generality, we may assume that
![]() $y_1,y_2$
are both adjacent to
$y_1,y_2$
are both adjacent to
![]() $x_k$
for some
$x_k$
for some
![]() $k \in [4]$
. Suppose that
$k \in [4]$
. Suppose that
![]() $y_1$
is also adjacent to
$y_1$
is also adjacent to
![]() $x_{\ell }$
. Let
$x_{\ell }$
. Let
![]() $H \;:\!=\; H' - x_1v + \{x_ky_1,x_ky_2,x_{\ell }y_1\} + \{x_ix_j \;:\; 1 \leq i \lt j \leq 4\}$
, see Figure 2(a). Then
$H \;:\!=\; H' - x_1v + \{x_ky_1,x_ky_2,x_{\ell }y_1\} + \{x_ix_j \;:\; 1 \leq i \lt j \leq 4\}$
, see Figure 2(a). Then
![]() $e(H) \geq e(H') + 8$
(since we add
$e(H) \geq e(H') + 8$
(since we add
![]() $9$
edges and delete at most
$9$
edges and delete at most
![]() $1$
), so
$1$
), so
![]() $e(H) \geq g_3(n-3) + 8 - 6 = g_3(n) - 6$
. Also,
$e(H) \geq g_3(n-3) + 8 - 6 = g_3(n) - 6$
. Also,
![]() $H' - x_1v$
is chordal because
$H' - x_1v$
is chordal because
![]() $x_1$
is a leaf or an isolated vertex in
$x_1$
is a leaf or an isolated vertex in
![]() $H'$
. Now observe that
$H'$
. Now observe that
![]() $H$
is chordal: adding first
$H$
is chordal: adding first
![]() $x_k$
, then
$x_k$
, then
![]() $x_{\ell }$
and then the other two vertices among
$x_{\ell }$
and then the other two vertices among
![]() $x_1,\dots,x_4$
, we add a simplicial vertex at each step.
$x_1,\dots,x_4$
, we add a simplicial vertex at each step.
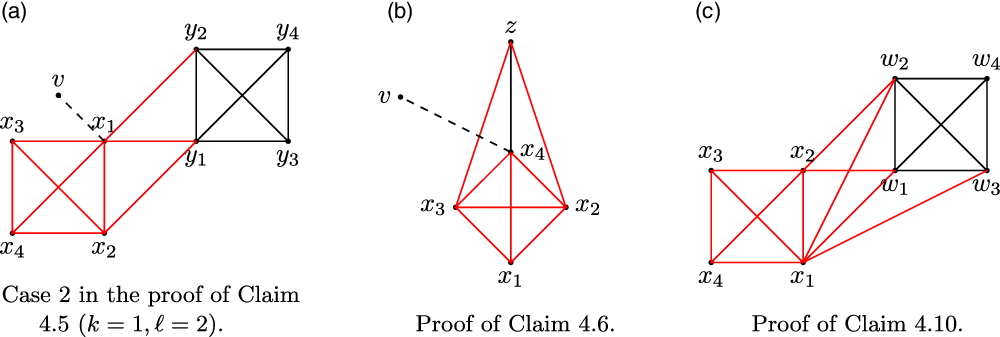
Figure 2. Illustrations to proofs of claims. The red edges are added after applying induction. The dashed edges are deleted.
Case 3:
![]() $a_2 = 0$
. Then there are at most
$a_2 = 0$
. Then there are at most
![]() $n-4$
edges between
$n-4$
edges between
![]() $x_1,\dots,x_4$
and
$x_1,\dots,x_4$
and
![]() $V(G) \setminus \{x_1,\dots,x_4\}$
. Also,
$V(G) \setminus \{x_1,\dots,x_4\}$
. Also,
![]() $d(x_1) + \dots + d(x_4) \leq n+8$
by (11). Let
$d(x_1) + \dots + d(x_4) \leq n+8$
by (11). Let
![]() $G'$
be the graph obtained from
$G'$
be the graph obtained from
![]() $G$
by deleting
$G$
by deleting
![]() $x_2,x_3,x_4$
and all edges touching
$x_2,x_3,x_4$
and all edges touching
![]() $x_1$
. Then
$x_1$
. Then
![]() $v(G') = n-3$
and
$v(G') = n-3$
and
![]() $e(G') \geq e(G) - (n + 2) = t_3(n) + 1 - (n + 2) = t_3(n-3) + 1 + n - 5$
. Note that
$e(G') \geq e(G) - (n + 2) = t_3(n) + 1 - (n + 2) = t_3(n-3) + 1 + n - 5$
. Note that
![]() $n \geq 8$
because else
$n \geq 8$
because else
![]() $e(G) \leq \binom{n-4}{2} + n - 4 + 6 \lt t_3(n)$
(where the last inequality holds for
$e(G) \leq \binom{n-4}{2} + n - 4 + 6 \lt t_3(n)$
(where the last inequality holds for
![]() $n \leq 7$
), a contradiction. So
$n \leq 7$
), a contradiction. So
![]() $v(G') \geq 5$
. By Lemma 4.4, there are distinct
$v(G') \geq 5$
. By Lemma 4.4, there are distinct
![]() $v_1,v_2,w_1,w_2,w_3 \in V(G')$
such that
$v_1,v_2,w_1,w_2,w_3 \in V(G')$
such that
![]() $v_i,w_1,w_2,w_3$
is a
$v_i,w_1,w_2,w_3$
is a
![]() $4$
-clique for
$4$
-clique for
![]() $i = 1,2$
. Let
$i = 1,2$
. Let
![]() $G''$
be the graph obtained from
$G''$
be the graph obtained from
![]() $G'$
by deleting all edges touching
$G'$
by deleting all edges touching
![]() $v_1$
. Then
$v_1$
. Then
![]() $v(G'') = n-3$
and
$v(G'') = n-3$
and
![]() $e(G'') \geq e(G') - (n-5)$
because
$e(G'') \geq e(G') - (n-5)$
because
![]() $v_1$
is not adjacent in
$v_1$
is not adjacent in
![]() $G'$
to
$G'$
to
![]() $x_1$
or to itself, leaving
$x_1$
or to itself, leaving
![]() $n-5$
potential neighbours. So
$n-5$
potential neighbours. So
![]() $e(G'') \geq t_3(n-3) + 1$
. By the induction hypothesis,
$e(G'') \geq t_3(n-3) + 1$
. By the induction hypothesis,
![]() $G''$
contains a chordal subgraph
$G''$
contains a chordal subgraph
![]() $H'$
with
$H'$
with
![]() $e(H') \geq g_3(n-3) - 6$
, such that
$e(H') \geq g_3(n-3) - 6$
, such that
![]() $H'$
contains the edges of the clique
$H'$
contains the edges of the clique
![]() $v_2,w_1,w_2,w_3$
. Let
$v_2,w_1,w_2,w_3$
. Let
![]() $H = H' + \{v_1w_i \;:\; 1 \leq i \leq 3\} + \{x_ix_j \;:\; 1 \leq i \lt j \leq 4\}$
. Then
$H = H' + \{v_1w_i \;:\; 1 \leq i \leq 3\} + \{x_ix_j \;:\; 1 \leq i \lt j \leq 4\}$
. Then
![]() $e(H) = e(H') + 9 \geq g_3(n) - 6$
, and it is easy to check that
$e(H) = e(H') + 9 \geq g_3(n) - 6$
, and it is easy to check that
![]() $H$
is chordal.
$H$
is chordal.
Claim 4.6.
We may assume that for every
![]() $i \in$
[Reference Edwards4], the following holds. If
$i \in$
[Reference Edwards4], the following holds. If
![]() $d(x_i) \geq \lfloor \frac{2n}{3} \rfloor + 1$
, then there is
$d(x_i) \geq \lfloor \frac{2n}{3} \rfloor + 1$
, then there is
![]() $y \in V(G) \setminus \{x_1,\dots,x_4\}$
such that
$y \in V(G) \setminus \{x_1,\dots,x_4\}$
such that
![]() $y$
is adjacent to
$y$
is adjacent to
![]() $x_i$
and to at least two vertices in
$x_i$
and to at least two vertices in
![]() $X \setminus \{x_i\}$
.
$X \setminus \{x_i\}$
.
Proof of Claim
4.6
. Without loss of generality,
![]() $i = 1$
. Suppose that
$i = 1$
. Suppose that
![]() $d(x_1) \geq \lfloor \frac{2n}{3} \rfloor + 1$
but there is no
$d(x_1) \geq \lfloor \frac{2n}{3} \rfloor + 1$
but there is no
![]() $y$
as above. We will show that the assertion of Theorem 4.1 holds. For
$y$
as above. We will show that the assertion of Theorem 4.1 holds. For
![]() $0 \leq j \leq 3$
, let
$0 \leq j \leq 3$
, let
![]() $A_j$
be the set of vertices
$A_j$
be the set of vertices
![]() $z \in V(G) \setminus \{x_2,x_3,x_4\}$
which are adjacent to exactly
$z \in V(G) \setminus \{x_2,x_3,x_4\}$
which are adjacent to exactly
![]() $j$
of the vertices
$j$
of the vertices
![]() $x_2,x_3,x_4$
, and let
$x_2,x_3,x_4$
, and let
![]() $a_j = |A_j|$
. Note that
$a_j = |A_j|$
. Note that
![]() $x_1 \in A_3$
. By Claim 4.5, we may assume that there exists
$x_1 \in A_3$
. By Claim 4.5, we may assume that there exists
![]() $z \in V(G) \setminus \{x_1,\dots,x_4\}$
which is adjacent to three of the vertices
$z \in V(G) \setminus \{x_1,\dots,x_4\}$
which is adjacent to three of the vertices
![]() $x_1,\dots,x_4$
. By assumption, these three vertices cannot include
$x_1,\dots,x_4$
. By assumption, these three vertices cannot include
![]() $x_1$
, so we must have
$x_1$
, so we must have
![]() $z \in A_3$
. Hence,
$z \in A_3$
. Hence,
![]() $A_3 \setminus \{x_1\} \neq \emptyset$
.
$A_3 \setminus \{x_1\} \neq \emptyset$
.
We have
![]() $a_0 + a_1 + a_2 + a_3 = n-3$
and
$a_0 + a_1 + a_2 + a_3 = n-3$
and
![]() $a_1 + 2a_2 + 3a_3 = d(x_2) + d(x_3) + d(x_4) - 6$
. So
$a_1 + 2a_2 + 3a_3 = d(x_2) + d(x_3) + d(x_4) - 6$
. So
![]() $a_2 + 2a_3 = d(x_2) + d(x_3) + d(x_4) - n - 3 + a_0$
. By assumption, there is no
$a_2 + 2a_3 = d(x_2) + d(x_3) + d(x_4) - n - 3 + a_0$
. By assumption, there is no
![]() $y \in V(G) \setminus \{x_1,\dots,x_4\}$
which is adjacent to
$y \in V(G) \setminus \{x_1,\dots,x_4\}$
which is adjacent to
![]() $x_1$
and belongs to
$x_1$
and belongs to
![]() $A_2 \cup A_3$
. Hence,
$A_2 \cup A_3$
. Hence,
![]() $d(x_1) \leq n - a_2 - a_3 = 2n - d(x_2) - d(x_3) - d(x_4) + 3 + a_3 - a_0$
. So we get
$d(x_1) \leq n - a_2 - a_3 = 2n - d(x_2) - d(x_3) - d(x_4) + 3 + a_3 - a_0$
. So we get
Pick a set of edges
![]() $F$
as follows:
$F$
as follows:
-
• Suppose first that
 $a_0 = 0$
. We claim that
$a_0 = 0$
. We claim that
 $A_1 \cup A_2 \neq \emptyset$
. Indeed, if
$A_1 \cup A_2 \neq \emptyset$
. Indeed, if
 $A_1 \cup A_2 = \emptyset$
then
$A_1 \cup A_2 = \emptyset$
then
 $A_3 = V(G) \setminus \{x_2,x_3,x_4\}$
. But then
$A_3 = V(G) \setminus \{x_2,x_3,x_4\}$
. But then
 $N(x_1) = \{x_2,x_3,x_4\}$
so
$N(x_1) = \{x_2,x_3,x_4\}$
so
 $d(x_1) = 3$
. On the other hand,
$d(x_1) = 3$
. On the other hand,
 $d(x_1) \geq \lfloor \frac{2n}{3} \rfloor + 1$
by assumption. So
$d(x_1) \geq \lfloor \frac{2n}{3} \rfloor + 1$
by assumption. So
 $\lfloor \frac{2n}{3} \rfloor \leq 2$
, which is false for every
$\lfloor \frac{2n}{3} \rfloor \leq 2$
, which is false for every
 $n \geq 5$
. Now pick an arbitrary
$n \geq 5$
. Now pick an arbitrary
 $v \in A_1 \cup A_2$
, and suppose without loss of generality that
$v \in A_1 \cup A_2$
, and suppose without loss of generality that
 $v$
is adjacent to
$v$
is adjacent to
 $x_4$
. Take
$x_4$
. Take
 $F$
to be the set of all edges between
$F$
to be the set of all edges between
 $x_4$
and
$x_4$
and
 $N(x_4) \setminus (A_3 \cup \{x_2,x_3,v\})$
. Note that
$N(x_4) \setminus (A_3 \cup \{x_2,x_3,v\})$
. Note that
 $|F| = d(x_4) - a_3 - 3$
.
$|F| = d(x_4) - a_3 - 3$
. -
• If
 $a_0 \geq 1$
then
$a_0 \geq 1$
then
 $F$
is the set of all edges between
$F$
is the set of all edges between
 $x_4$
and
$x_4$
and
 $N(x_4) \setminus (A_3 \cup \{x_2,x_3\})$
. Then
$N(x_4) \setminus (A_3 \cup \{x_2,x_3\})$
. Then
 $|F| = d(x_4) - a_3 - 2$
.
$|F| = d(x_4) - a_3 - 2$
.
In both cases we have
![]() $|F| \leq d(x_4) - a_3 - 3 + a_0$
. Let
$|F| \leq d(x_4) - a_3 - 3 + a_0$
. Let
![]() $G'$
be the graph obtained from
$G'$
be the graph obtained from
![]() $G$
by deleting
$G$
by deleting
![]() $x_1,x_2,x_3$
and all edges in
$x_1,x_2,x_3$
and all edges in
![]() $F$
. So
$F$
. So
![]() $v(G') = n-3$
. To count the deleted edges, note that there are
$v(G') = n-3$
. To count the deleted edges, note that there are
![]() $d(x_1) + d(x_2) + d(x_3) - 3$
edges touching
$d(x_1) + d(x_2) + d(x_3) - 3$
edges touching
![]() $x_1,x_2,x_3$
, and that the edges in
$x_1,x_2,x_3$
, and that the edges in
![]() $F$
do not touch
$F$
do not touch
![]() $x_1,x_2,x_3$
. So the number of deleted edges is
$x_1,x_2,x_3$
. So the number of deleted edges is
where the last inequality uses (12). So
![]() $e(G') \geq e(G) - 2n + 3 = t_3(n) + 1 - 2n + 3 = t_3(n-3) + 1$
. By the induction hypothesis,
$e(G') \geq e(G) - 2n + 3 = t_3(n) + 1 - 2n + 3 = t_3(n-3) + 1$
. By the induction hypothesis,
![]() $G'$
contains a chordal subgraph
$G'$
contains a chordal subgraph
![]() $H'$
with
$H'$
with
![]() $e(H') \geq g_3(n-3) - 6$
. Define a subgraph
$e(H') \geq g_3(n-3) - 6$
. Define a subgraph
![]() $H''$
of
$H''$
of
![]() $G'$
as follows:
$G'$
as follows:
-
• If there is
 $z \in A_3 \setminus \{x_1\}$
such that
$z \in A_3 \setminus \{x_1\}$
such that
 $x_4z \in E(H')$
, then
$x_4z \in E(H')$
, then
 $H'' = H'$
;
$H'' = H'$
; -
• Else, pick any
 $z \in A_3 \setminus \{x_1\}$
and set
$z \in A_3 \setminus \{x_1\}$
and set
 $H'' = H' - x_4v + x_4z$
.
$H'' = H' - x_4v + x_4z$
.
We claim that
![]() $e(H'') \geq e(H')$
. In the first item this is obvious. Suppose we are in the second item. By the definition of
$e(H'') \geq e(H')$
. In the first item this is obvious. Suppose we are in the second item. By the definition of
![]() $F$
, every neighbour of
$F$
, every neighbour of
![]() $x_4$
in
$x_4$
in
![]() $G'$
belongs to
$G'$
belongs to
![]() $\{v\} \cup A_3 \setminus \{x_1\}$
. Since we are in the second item, the only possible neighbour of
$\{v\} \cup A_3 \setminus \{x_1\}$
. Since we are in the second item, the only possible neighbour of
![]() $x_4$
in
$x_4$
in
![]() $H'$
is
$H'$
is
![]() $v$
. So indeed
$v$
. So indeed
![]() $e(H'') \geq e(H')$
. Also,
$e(H'') \geq e(H')$
. Also,
![]() $H''$
is chordal; in the second case, this is because
$H''$
is chordal; in the second case, this is because
![]() $x_4$
is a leaf in both
$x_4$
is a leaf in both
![]() $H'$
and
$H'$
and
![]() $H''$
.
$H''$
.
By the definition of
![]() $H''$
, there is
$H''$
, there is
![]() $z \in A_3 \setminus \{x_1\}$
such that
$z \in A_3 \setminus \{x_1\}$
such that
![]() $x_4z \in E(H'')$
. Now put
$x_4z \in E(H'')$
. Now put
![]() $H = H'' + \{x_2z,x_3z\} + \{x_ix_j \;:\; 1 \leq i \lt j \leq 4\}$
, see Figure 2(b). Then
$H = H'' + \{x_2z,x_3z\} + \{x_ix_j \;:\; 1 \leq i \lt j \leq 4\}$
, see Figure 2(b). Then
![]() $e(H) = e(H'') + 8 \geq g_3(n-3) + 8 - 6 = g_3(n) - 6$
. Also,
$e(H) = e(H'') + 8 \geq g_3(n-3) + 8 - 6 = g_3(n) - 6$
. Also,
![]() $H$
is chordal: adding the vertices
$H$
is chordal: adding the vertices
![]() $x_2,x_3,x_1$
in this order, we always add a simplicial vertex. This proves Claim 4.6.
$x_2,x_3,x_1$
in this order, we always add a simplicial vertex. This proves Claim 4.6.
We now continue with the proof of the theorem. For
![]() $i \in [4]$
, we say that
$i \in [4]$
, we say that
![]() $x_i$
is deletable if
$x_i$
is deletable if
![]() $d(x_i) \leq \lfloor \frac{2n}{3} \rfloor$
, and there is
$d(x_i) \leq \lfloor \frac{2n}{3} \rfloor$
, and there is
![]() $y \in V(G) \setminus \{x_1,\dots,x_4\}$
which is adjacent to
$y \in V(G) \setminus \{x_1,\dots,x_4\}$
which is adjacent to
![]() $x_j$
for all
$x_j$
for all
![]() $j \in [4] \setminus \{i\}$
.
$j \in [4] \setminus \{i\}$
.
Claim 4.7.
We may assume that there is no deletable
![]() $x_i$
.
$x_i$
.
Proof. Suppose that
![]() $x_i$
is deletable. Without loss of generality, assume that
$x_i$
is deletable. Without loss of generality, assume that
![]() $i = 1$
. Let
$i = 1$
. Let
![]() $G' = G - x_1$
. Then
$G' = G - x_1$
. Then
![]() $e(G') = e(G) - d(x_1) \geq t_3(n) + 1 -\lfloor \frac{2n}{3} \rfloor = t_3(n-1) + 1$
. Let
$e(G') = e(G) - d(x_1) \geq t_3(n) + 1 -\lfloor \frac{2n}{3} \rfloor = t_3(n-1) + 1$
. Let
![]() $y$
be a common neighbour of
$y$
be a common neighbour of
![]() $x_2,x_3,x_4$
. By the induction hypothesis,
$x_2,x_3,x_4$
. By the induction hypothesis,
![]() $G'$
contains a chordal subgraph
$G'$
contains a chordal subgraph
![]() $H'$
with
$H'$
with
![]() $e(H') \geq g_3(n-1) - 6$
, such that
$e(H') \geq g_3(n-1) - 6$
, such that
![]() $H'$
contains the edges of the clique
$H'$
contains the edges of the clique
![]() $x_2,x_3,x_4,y$
. Take
$x_2,x_3,x_4,y$
. Take
![]() $H = H' + \{x_1x_2,x_1x_3,x_1x_4\}$
. Then
$H = H' + \{x_1x_2,x_1x_3,x_1x_4\}$
. Then
![]() $H$
is chordal and
$H$
is chordal and
![]() $e(H) = e(H') + 3 \geq g_3(n-1) + 3 - 6 \geq g_3(n) - 6$
.
$e(H) = e(H') + 3 \geq g_3(n-1) + 3 - 6 \geq g_3(n) - 6$
.
Claim 4.8.
We may assume that
![]() $d(x_1) + \dots + d(x_4) \leq g_3(n) - 1$
.
$d(x_1) + \dots + d(x_4) \leq g_3(n) - 1$
.
Proof. Else, take
![]() $H$
to be the subgraph of
$H$
to be the subgraph of
![]() $G$
consisting of all edges which touch
$G$
consisting of all edges which touch
![]() $x_1,\dots,x_4$
. Then
$x_1,\dots,x_4$
. Then
![]() $H$
is chordal and
$H$
is chordal and
![]() $e(H) = d(x_1) + \dots + d(x_4) - 6 \geq g_3(n) - 6$
.
$e(H) = d(x_1) + \dots + d(x_4) - 6 \geq g_3(n) - 6$
.
Claim 4.9.
We may assume that there is no
![]() $5$
-clique containing
$5$
-clique containing
![]() $x_1,\dots,x_4$
.
$x_1,\dots,x_4$
.
Proof. Suppose that
![]() $x_1,\dots,x_4,y$
is a
$x_1,\dots,x_4,y$
is a
![]() $5$
-clique. If
$5$
-clique. If
![]() $d(x_i) \leq \lfloor \frac{2n}{3} \rfloor$
then
$d(x_i) \leq \lfloor \frac{2n}{3} \rfloor$
then
![]() $x_i$
is deletable. Assuming no
$x_i$
is deletable. Assuming no
![]() $x_i$
is deletable, we have
$x_i$
is deletable, we have
![]() $d(x_1) + \dots + d(x_4) \geq 4 \cdot (\lfloor \frac{2n}{3} \rfloor + 1) \geq 2n + \lfloor \frac{2n}{3}\rfloor + 2= g_3(n)$
, so we are done by Claim 4.8.
$d(x_1) + \dots + d(x_4) \geq 4 \cdot (\lfloor \frac{2n}{3} \rfloor + 1) \geq 2n + \lfloor \frac{2n}{3}\rfloor + 2= g_3(n)$
, so we are done by Claim 4.8.
Claim 4.10.
We may assume that for every
![]() $i \in [4]$
,
$i \in [4]$
,
![]() $\sum _{j \neq i}{d(x_j)} \leq 2n$
.
$\sum _{j \neq i}{d(x_j)} \leq 2n$
.
Proof. Suppose that
![]() $d(x_1) + d(x_2) + d(x_3) \geq 2n+1$
(the proof for each other
$d(x_1) + d(x_2) + d(x_3) \geq 2n+1$
(the proof for each other
![]() $i$
is symmetric). By Claim 4.8, we may assume that
$i$
is symmetric). By Claim 4.8, we may assume that
![]() $d(x_4) \leq g_3(n) - 1 - (2n+1) = n - \lceil \frac{n}{3}\rceil = \lfloor \frac{2n}{3} \rfloor$
. By Claim 4.7, we may assume that
$d(x_4) \leq g_3(n) - 1 - (2n+1) = n - \lceil \frac{n}{3}\rceil = \lfloor \frac{2n}{3} \rfloor$
. By Claim 4.7, we may assume that
![]() $x_4$
is not deletable. Then
$x_4$
is not deletable. Then
![]() $x_1,x_2,x_3$
have no common neighbour except for
$x_1,x_2,x_3$
have no common neighbour except for
![]() $x_4$
. But as
$x_4$
. But as
![]() $d(x_1) + d(x_2) + d(x_3) \geq 2n+1$
, this means that every vertex in
$d(x_1) + d(x_2) + d(x_3) \geq 2n+1$
, this means that every vertex in
![]() $V(G) \setminus \{x_1,\dots,x_4\}$
is adjacent to exactly two of the vertices
$V(G) \setminus \{x_1,\dots,x_4\}$
is adjacent to exactly two of the vertices
![]() $x_1,x_2,x_3$
. Let
$x_1,x_2,x_3$
. Let
![]() $G' = G - \{x_1,\dots,x_4\}$
. Then
$G' = G - \{x_1,\dots,x_4\}$
. Then
![]() $v(G') = n-4$
and
$v(G') = n-4$
and
![]() $e(G') = e(G) - (d(x_1) + \dots + d(x_4)) + 6 \geq e(G) - g_3(n) + 7 = t_3(n) + 1 - g_3(n) + 7 = t_3(n-4) + 1$
by Lemma 4.2. Fix an arbitrary
$e(G') = e(G) - (d(x_1) + \dots + d(x_4)) + 6 \geq e(G) - g_3(n) + 7 = t_3(n) + 1 - g_3(n) + 7 = t_3(n-4) + 1$
by Lemma 4.2. Fix an arbitrary
![]() $4$
-clique
$4$
-clique
![]() $w_1,\dots,w_4$
in
$w_1,\dots,w_4$
in
![]() $G'$
. By the induction hypothesis,
$G'$
. By the induction hypothesis,
![]() $G'$
contains a chordal subgraph
$G'$
contains a chordal subgraph
![]() $H'$
with
$H'$
with
![]() $e(H') \geq g_3(n-4) - 6$
such that
$e(H') \geq g_3(n-4) - 6$
such that
![]() $H'$
contains the edges of the clique
$H'$
contains the edges of the clique
![]() $w_1,\dots,w_4$
. Each
$w_1,\dots,w_4$
. Each
![]() $w_i$
is adjacent to two of the vertices
$w_i$
is adjacent to two of the vertices
![]() $x_1,x_2,x_3$
. By the pigeonhole principle and by symmetry, we may assume that each of
$x_1,x_2,x_3$
. By the pigeonhole principle and by symmetry, we may assume that each of
![]() $w_1,w_2$
is adjacent to
$w_1,w_2$
is adjacent to
![]() $x_1,x_2$
. Moreover,
$x_1,x_2$
. Moreover,
![]() $w_3$
must be adjacent to
$w_3$
must be adjacent to
![]() $x_1$
or
$x_1$
or
![]() $x_2$
; say to
$x_2$
; say to
![]() $x_1$
. Take
$x_1$
. Take
![]() $H = H' + \{x_1w_1,x_1w_2,x_1w_3,x_2w_1,x_2w_2\} + \{x_ix_j \;:\; 1 \leq i \lt j \leq 4\}$
, see Figure 2(c). Then
$H = H' + \{x_1w_1,x_1w_2,x_1w_3,x_2w_1,x_2w_2\} + \{x_ix_j \;:\; 1 \leq i \lt j \leq 4\}$
, see Figure 2(c). Then
![]() $e(H) = e(H') + 11 \geq g_3(n-4) + 11 - 6 \geq g_3(n) - 6$
. Also,
$e(H) = e(H') + 11 \geq g_3(n-4) + 11 - 6 \geq g_3(n) - 6$
. Also,
![]() $H$
is chordal: adding the vertices
$H$
is chordal: adding the vertices
![]() $x_1,x_2,x_3,x_4$
in this order, we always add a simplicial vertex. This proves Claim 4.10.
$x_1,x_2,x_3,x_4$
in this order, we always add a simplicial vertex. This proves Claim 4.10.
By Claim 4.5, we may assume that there is
![]() $y_0 \in V(G) \setminus \{x_1,\dots,x_4\}$
which is adjacent to at least 3 of the vertices
$y_0 \in V(G) \setminus \{x_1,\dots,x_4\}$
which is adjacent to at least 3 of the vertices
![]() $x_1,\dots,x_4$
; say to
$x_1,\dots,x_4$
; say to
![]() $x_2,x_3,x_4$
. By Claim 4.7, we may assume that
$x_2,x_3,x_4$
. By Claim 4.7, we may assume that
![]() $x_i$
is not deletable for any
$x_i$
is not deletable for any
![]() $i \in [4]$
. Since
$i \in [4]$
. Since
![]() $x_1$
is not deletable,
$x_1$
is not deletable,
![]() $d(x_1) \geq \lfloor \frac{2n}{3} \rfloor + 1$
. By Claim 4.6, there is
$d(x_1) \geq \lfloor \frac{2n}{3} \rfloor + 1$
. By Claim 4.6, there is
![]() $z_0 \in V(G) \setminus \{x_1,\dots,x_4\}$
which is adjacent to
$z_0 \in V(G) \setminus \{x_1,\dots,x_4\}$
which is adjacent to
![]() $x_1$
and to at least two of the vertices
$x_1$
and to at least two of the vertices
![]() $x_2,x_3,x_4$
; without loss of generality,
$x_2,x_3,x_4$
; without loss of generality,
![]() $z_0$
is adjacent to
$z_0$
is adjacent to
![]() $x_3,x_4$
. Since
$x_3,x_4$
. Since
![]() $x_2$
is not deletable, we have
$x_2$
is not deletable, we have
![]() $d(x_2) \geq \lfloor \frac{2n}{3} \rfloor + 1$
. Also, we may assume that
$d(x_2) \geq \lfloor \frac{2n}{3} \rfloor + 1$
. Also, we may assume that
![]() $y_0 \neq z_0$
because else we would have a
$y_0 \neq z_0$
because else we would have a
![]() $5$
-clique containing
$5$
-clique containing
![]() $x_1,\dots,x_4$
.
$x_1,\dots,x_4$
.
Claim 4.11.
We may assume that
![]() $d(x_i) \leq \lfloor \frac{2n}{3} \rfloor$
for each
$d(x_i) \leq \lfloor \frac{2n}{3} \rfloor$
for each
![]() $i = 3,4$
.
$i = 3,4$
.
Proof. By Claim 4.10, we may assume that
![]() $d(x_i) \leq 2n - d(x_1) - d(x_2) \leq 2n - 2 \cdot \left ( \lfloor \frac{2n}{3} \rfloor + 1 \right ) \leq \lfloor \frac{2n}{3} \rfloor$
.
$d(x_i) \leq 2n - d(x_1) - d(x_2) \leq 2n - 2 \cdot \left ( \lfloor \frac{2n}{3} \rfloor + 1 \right ) \leq \lfloor \frac{2n}{3} \rfloor$
.
If
![]() $d(y_0) \leq \lfloor \frac{2n}{3} \rfloor$
then we can delete
$d(y_0) \leq \lfloor \frac{2n}{3} \rfloor$
then we can delete
![]() $y_0$
, apply induction to the remaining graph to find a chordal subgraph
$y_0$
, apply induction to the remaining graph to find a chordal subgraph
![]() $H'$
with at least
$H'$
with at least
![]() $g_3(n-1)-6$
edges which contains the edges of the clique
$g_3(n-1)-6$
edges which contains the edges of the clique
![]() $x_1,\dots,x_4$
and then add the edges
$x_1,\dots,x_4$
and then add the edges
![]() $x_2y_0,x_3y_0,x_4y_0$
to
$x_2y_0,x_3y_0,x_4y_0$
to
![]() $H'$
to conclude the proof. So suppose that
$H'$
to conclude the proof. So suppose that
![]() $d(y_0) \geq \lfloor \frac{2n}{3} \rfloor +1$
. Let
$d(y_0) \geq \lfloor \frac{2n}{3} \rfloor +1$
. Let
![]() $v \notin \{x_3,x_4\}$
be a common neighbour of
$v \notin \{x_3,x_4\}$
be a common neighbour of
![]() $x_2$
and
$x_2$
and
![]() $y_0$
. Such a vertex
$y_0$
. Such a vertex
![]() $v$
exists because
$v$
exists because
![]() $d(x_2) + d(y_0) \geq 2 \cdot \left ( \lfloor \frac{2n}{3} \rfloor + 1 \right ) \geq n+3$
, where the last inequality holds for every
$d(x_2) + d(y_0) \geq 2 \cdot \left ( \lfloor \frac{2n}{3} \rfloor + 1 \right ) \geq n+3$
, where the last inequality holds for every
![]() $n \geq 5$
. Note that
$n \geq 5$
. Note that
![]() $v \neq x_1$
because
$v \neq x_1$
because
![]() $x_1$
is not adjacent to
$x_1$
is not adjacent to
![]() $y_0$
, as otherwise
$y_0$
, as otherwise
![]() $x_1,\dots,x_4,y_0$
would be a
$x_1,\dots,x_4,y_0$
would be a
![]() $5$
-clique. Similarly,
$5$
-clique. Similarly,
![]() $v \neq z_0$
because
$v \neq z_0$
because
![]() $v$
is adjacent to
$v$
is adjacent to
![]() $x_2$
and
$x_2$
and
![]() $z_0$
is adjacent to
$z_0$
is adjacent to
![]() $x_1,x_3,x_4$
(so otherwise
$x_1,x_3,x_4$
(so otherwise
![]() $x_1,\dots,x_4,z_0$
would be a
$x_1,\dots,x_4,z_0$
would be a
![]() $5$
-clique).
$5$
-clique).
Suppose first that
![]() $x_2,y_0,v$
have no common neighbour. Then
$x_2,y_0,v$
have no common neighbour. Then
![]() $d(x_2) + d(y_0) + d(v) \leq 2n$
. Let
$d(x_2) + d(y_0) + d(v) \leq 2n$
. Let
![]() $G' = G - \{x_2,y_0,v\}$
. Then
$G' = G - \{x_2,y_0,v\}$
. Then
![]() $e(G') = e(G) - d(x_2) - d(y_0) - d(v) + 3 \geq t_3(n) + 1 - 2n + 3 = t_3 (n-3) + 1$
. By the induction hypothesis,
$e(G') = e(G) - d(x_2) - d(y_0) - d(v) + 3 \geq t_3(n) + 1 - 2n + 3 = t_3 (n-3) + 1$
. By the induction hypothesis,
![]() $G'$
contains a chordal subgraph
$G'$
contains a chordal subgraph
![]() $H'$
with
$H'$
with
![]() $e(H') \geq g_3(n-3) - 6$
such that
$e(H') \geq g_3(n-3) - 6$
such that
![]() $H'$
contains the edges of the clique
$H'$
contains the edges of the clique
![]() $x_1,x_3,x_4,z_0$
. Take
$x_1,x_3,x_4,z_0$
. Take
![]() $H = H' + \{x_2x_1,x_2x_3,x_2x_4,y_0x_2,y_0x_3,y_0x_4,vx_2,vy_0\}$
, see Figure 3(a). Then
$H = H' + \{x_2x_1,x_2x_3,x_2x_4,y_0x_2,y_0x_3,y_0x_4,vx_2,vy_0\}$
, see Figure 3(a). Then
![]() $e(H) = e(H') + 8 \geq g_3(n-3) + 8 - 6 = g_3(n) - 6$
. Also,
$e(H) = e(H') + 8 \geq g_3(n-3) + 8 - 6 = g_3(n) - 6$
. Also,
![]() $H$
is chordal: adding the vertices
$H$
is chordal: adding the vertices
![]() $x_2,y_0,v$
in this order, we always add a simplicial vertex.
$x_2,y_0,v$
in this order, we always add a simplicial vertex.

Figure 3. Applying induction after deleting certain vertices. The added edges are red.
Suppose now that
![]() $x_2,y_0,v$
have a common neighbour
$x_2,y_0,v$
have a common neighbour
![]() $w$
. First, suppose that
$w$
. First, suppose that
![]() $w \in \{x_3,x_4\}$
, say
$w \in \{x_3,x_4\}$
, say
![]() $w = x_3$
. Let
$w = x_3$
. Let
![]() $G' = G - \{x_1,x_4\}$
. We have
$G' = G - \{x_1,x_4\}$
. We have
![]() $d(x_1) + d(x_4) \leq 2n - d(x_2) \leq 2n - \lfloor \frac{2n}{3} \rfloor - 1 \leq \lfloor \frac{4n}{3} \rfloor$
, where the first inequality is by Claim 4.10. So
$d(x_1) + d(x_4) \leq 2n - d(x_2) \leq 2n - \lfloor \frac{2n}{3} \rfloor - 1 \leq \lfloor \frac{4n}{3} \rfloor$
, where the first inequality is by Claim 4.10. So
![]() $e(G') = e(G) - d(x_1) - d(x_4) + 1 \geq t_3(n) + 1 - \lfloor \frac{4n}{3} \rfloor + 1 = t_3(n-2) + 1$
. By the induction hypothesis,
$e(G') = e(G) - d(x_1) - d(x_4) + 1 \geq t_3(n) + 1 - \lfloor \frac{4n}{3} \rfloor + 1 = t_3(n-2) + 1$
. By the induction hypothesis,
![]() $G'$
has a chordal subgraph
$G'$
has a chordal subgraph
![]() $H'$
with
$H'$
with
![]() $e(H') \geq g_3(n-2) - 6$
such that
$e(H') \geq g_3(n-2) - 6$
such that
![]() $H'$
contains the edges of the clique
$H'$
contains the edges of the clique
![]() $x_2,y_0,v,x_3$
. Take
$x_2,y_0,v,x_3$
. Take
![]() $H = H' + \{x_4x_2,x_4x_3,x_4y_0,x_1x_2,x_1x_3,x_1x_4\}$
, see Figure 3(b). Then
$H = H' + \{x_4x_2,x_4x_3,x_4y_0,x_1x_2,x_1x_3,x_1x_4\}$
, see Figure 3(b). Then
![]() $e(H) = e(H') + 6 \geq g_3(n-2) + 6 - 6 \geq g_3(n) - 6$
. Also,
$e(H) = e(H') + 6 \geq g_3(n-2) + 6 - 6 \geq g_3(n) - 6$
. Also,
![]() $H$
is chordal: adding
$H$
is chordal: adding
![]() $x_4$
and then
$x_4$
and then
![]() $x_1$
, we always add a simplicial vertex. Now suppose that
$x_1$
, we always add a simplicial vertex. Now suppose that
![]() $w \notin \{x_3,x_4\}$
. Let
$w \notin \{x_3,x_4\}$
. Let
![]() $G' = G - \{x_1,x_3,x_4\}$
. By Claims 4.10 and 4.11, we have
$G' = G - \{x_1,x_3,x_4\}$
. By Claims 4.10 and 4.11, we have
![]() $d(x_1) + d(x_3) \leq 2n - d(x_2) \leq \frac{4n}{3}$
and
$d(x_1) + d(x_3) \leq 2n - d(x_2) \leq \frac{4n}{3}$
and
![]() $d(x_4) \leq \frac{2n}{3}$
, so
$d(x_4) \leq \frac{2n}{3}$
, so
![]() $d(x_1) + d(x_3) + d(x_4) \leq 2n$
. Hence,
$d(x_1) + d(x_3) + d(x_4) \leq 2n$
. Hence,
![]() $e(G') = e(G) - d(x_1) - d(x_3) - d(x_4) + 3 \geq t_3(n) + 1 - 2n + 3 = t_3(n-3) + 1$
. By the induction hypothesis,
$e(G') = e(G) - d(x_1) - d(x_3) - d(x_4) + 3 \geq t_3(n) + 1 - 2n + 3 = t_3(n-3) + 1$
. By the induction hypothesis,
![]() $G'$
has a chordal subgraph
$G'$
has a chordal subgraph
![]() $H'$
with
$H'$
with
![]() $e(H') \geq g_3(n-3) - 6$
such that
$e(H') \geq g_3(n-3) - 6$
such that
![]() $H'$
contains the edges of the clique
$H'$
contains the edges of the clique
![]() $x_2,y_0,v,w$
. Now take
$x_2,y_0,v,w$
. Now take
![]() $H = H' + \{x_3y_0,x_4y_0\} + \{x_ix_j \;:\; 1 \leq i \lt j \leq 4\}$
, see Figure 3(c). Then
$H = H' + \{x_3y_0,x_4y_0\} + \{x_ix_j \;:\; 1 \leq i \lt j \leq 4\}$
, see Figure 3(c). Then
![]() $e(H) = e(H') + 8 \geq g_3(n-3) + 8 - 6 = g_3(n) - 6$
. Also,
$e(H) = e(H') + 8 \geq g_3(n-3) + 8 - 6 = g_3(n) - 6$
. Also,
![]() $H$
is chordal: adding the vertices
$H$
is chordal: adding the vertices
![]() $x_3,x_4,x_1$
in this order, we always add a simplicial vertex. This completes the proof of the theorem.
$x_3,x_4,x_1$
in this order, we always add a simplicial vertex. This completes the proof of the theorem.
5. Concluding remarks
In this paper we study the maximal value
![]() $f(n,m)$
such that every graph with
$f(n,m)$
such that every graph with
![]() $n$
vertices and
$n$
vertices and
![]() $m$
edges has a chordal subgraph with at least
$m$
edges has a chordal subgraph with at least
![]() $f(n,m)$
edges. We determine this function asymptotically for all
$f(n,m)$
edges. We determine this function asymptotically for all
![]() $m$
and exactly for
$m$
and exactly for
![]() $m \leq t_3(n)+1$
. Our results suggest the following conjecture on the value of
$m \leq t_3(n)+1$
. Our results suggest the following conjecture on the value of
![]() $f(n,m)$
for general
$f(n,m)$
for general
![]() $m$
.
$m$
.
Conjecture 5.1.
Let
![]() $k \geq 2$
,
$k \geq 2$
,
![]() $n \geq 1$
and
$n \geq 1$
and
![]() $t_{k}(n)+1 \leq m \leq t_{k+1}(n)$
. Then
$t_{k}(n)+1 \leq m \leq t_{k+1}(n)$
. Then
where the minimum is taken over all
![]() $t,r \geq 0$
satisfying
$t,r \geq 0$
satisfying
![]() $t_{k-1}(n-t) + t(n-t) + t_2(r) \geq m$
.
$t_{k-1}(n-t) + t(n-t) + t_2(r) \geq m$
.
It seems very likely that some progress on this conjecture can be achieved using our techniques together with a careful case analysis, but it would be interesting to find a proof which avoids such a case analysis as much as possible.
Note added:
Zachary Hunter (personal communication) very recently improved the error term in Theorem 1.3 from
![]() $O(\sqrt{n})$
to
$O(\sqrt{n})$
to
![]() $O(1)$
in the special case
$O(1)$
in the special case
![]() $m = t_k(n)+1$
, proving that
$m = t_k(n)+1$
, proving that
![]() $f(n,t_k(n)+1) = (k-1/k)n - O_k(1)$
.
$f(n,t_k(n)+1) = (k-1/k)n - O_k(1)$
.
Acknowledgements
The authors would like to thank the anonymous referee for a careful reading of the paper and useful suggestions.
Funding
Research supported in part by SNSF grant 200021_196965