Hostname: page-component-848d4c4894-cjp7w Total loading time: 0 Render date: 2024-06-30T01:14:51.693Z Has data issue: false hasContentIssue false
  • English
  • Français

Largest Components in Random Hypergraphs

Published online by Cambridge University Press:  04 April 2018

OLIVER COOLEY ,
MIHYUN KANG  and
YURY PERSON
OLIVER COOLEY
Affiliation:
Institute of Discrete Mathematics, Graz University of Technology, Steyrergasse 30, 8010 Graz, Austria (e-mail: cooley@math.tugraz.at, kang@math.tugraz.at)
MIHYUN KANG
Affiliation:
Institute of Discrete Mathematics, Graz University of Technology, Steyrergasse 30, 8010 Graz, Austria (e-mail: cooley@math.tugraz.at, kang@math.tugraz.at)
YURY PERSON
Affiliation:
Goethe-Universität, Institute of Mathematics, Robert-Mayer-Strasse 10, 60325 Frankfurt, Germany (e-mail: person@math.uni-frankfurt.de)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we consider j-tuple-connected components in random k-uniform hypergraphs (the j-tuple-connectedness relation can be defined by letting two j-sets be connected if they lie in a common edge and considering the transitive closure; the case j = 1 corresponds to the common notion of vertex-connectedness). We show that the existence of a j-tuple-connected component containing Θ(nj) j-sets undergoes a phase transition and show that the threshold occurs at edge probability

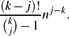$$\frac{(k-j)!}{\binom{k}{j}-1}n^{j-k}.$$
Our proof extends the recent short proof for the graph case by Krivelevich and Sudakov, which makes use of a depth-first search to reveal the edges of a random graph.

Our main original contribution is a bounded degree lemma, which controls the structure of the component grown in the search process.

Keywords

Primary 05C65Secondary 05C80
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 27 , Issue 5 , September 2018 , pp. 741 - 762
Copyright
Copyright © Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

The first and third authors were supported by short visit grants 5639 and 5472, respectively, from the European Science Foundation (ESF) within the ‘Random Geometry of Large Interacting Systems and Statistical Physics’ (RGLIS) programme.

‡

The second author is supported by Austrian Science Fund (FWF): P26826, W1230, Doctoral Programme ‘Discrete Mathematics’.

References

[1] Aronshtam, L. and Linial, N. (2015) When does the top homology of a random simplicial complex vanish? Random Struct. Alg. 46 26–35.Google Scholar
[2] Aronshtam, L. and Linial, N. (2016) The threshold for d-collapsibility in random complexes. Random Struct. Alg. 48 260–269.Google Scholar
[3] Aronshtam, L., Linial, N., Łuczak, T. and Meshulam, R. (2013) Collapsibility and vanishing of top homology in random simplicial complexes. Discrete Comput. Geom. 49, no. 2, 317–334.Google Scholar
[4] Behrisch, M., Coja-Oghlan, A. and Kang, M. (2010) The order of the giant component of random hypergraphs. Random Struct. Alg. 36 149–184.Google Scholar
[5] Behrisch, M., Coja-Oghlan, A. and Kang, M. (2014) Local limit theorems for the giant component of random hypergraphs. Combin. Probab. Comput. 23 331–366.Google Scholar
[6] Bohman, T. (2009) The triangle-free process. Adv. Math. 221 1653–1677.Google Scholar
[7] Bollobás, B. (1984) The evolution of random graphs. Trans. Amer. Math. Soc. 286 257–274.Google Scholar
[8] Bollobás, B. (2001) Random Graphs, second edition, Cambridge University Press.Google Scholar
[9] Bollobás, B. and Riordan, O. (2012) Asymptotic normality of the size of the giant component in a random hypergraph. Random Struct. Alg. 41 441–450.Google Scholar
[10] Cooley, O., Kang, M. and Koch, K. The size of the giant component in random hypergraphs. Random Struct. Alg., DOI: 10.1002/rsa.20761.Google Scholar
[11] Erdős, P. and Rényi, A. (1960) On the evolution of random graphs. Magyar Tud. Akad. Mat. Kutató Int. Közl. 5 17–61.Google Scholar
[12] Janson, S., Łuczak, T. and A. Ruciński, A. (2000) Random Graphs, Wiley.Google Scholar
[13] Karoński, M. and Łuczak, T. (2002) The phase transition in a random hypergraph. J. Comput. Appl. Math. 142 125–135.Google Scholar
[14] Krivelevich, M. and Sudakov, B. (2013) The phase transition in random graphs: A simple proof. Random Struct. Alg. 43 131–138.Google Scholar
[15] Linial, N. and Meshulam, R. (2006) Homological connectivity of random 2-complexes. Combinatorica 26 475–487.Google Scholar
[16] Lu, L. and Peng, X. High-order phase transition in random hypergraphs. arXiv:1409.1174Google Scholar
[17] Łuczak, T. (1990) Component behavior near the critical point of the random graph process. Random Struct. Alg. 1 287–310.Google Scholar
[18] Molloy, M. (2005) Cores in random hypergraphs and boolean formulas. Random Struct. Alg. 27 124–135.Google Scholar
[19] Nachmias, A. and Peres, Y. (2010) The critical random graph, with martingales. Israel J. Math. 176 29–41.Google Scholar
[20] Ravelomanana, and Rijamamy, (2006) Creation and growth of components in a random hypergraph process. In COCOON 2006: Computing and Combinatorics, Springer, pp. 350–359.Google Scholar
[21] Schmidt-Pruzan, J. and E. Shamir, E. (1985) Component structure in the evolution of random hypergraphs. Combinatorica 5 81–94.Google Scholar