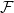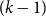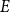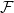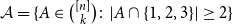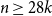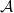1. Introduction
Let
![]() $n\gt k\gt t$
be positive integers and let
$n\gt k\gt t$
be positive integers and let
![]() $[n]=\{1,2,\ldots,n\}$
be the standard
$[n]=\{1,2,\ldots,n\}$
be the standard
![]() $n$
-element set. For
$n$
-element set. For
![]() $1\leq i\lt j\leq n$
, let
$1\leq i\lt j\leq n$
, let
![]() $[i,j]=\{i,i+1,\ldots,j\}$
. Let
$[i,j]=\{i,i+1,\ldots,j\}$
. Let
![]() $\binom{[n]}{k}$
denote the collection of all
$\binom{[n]}{k}$
denote the collection of all
![]() $k$
-subsets of
$k$
-subsets of
![]() $[n]$
. Subsets of
$[n]$
. Subsets of
![]() $\binom{[n]}{k}$
are called
$\binom{[n]}{k}$
are called
![]() $k$
-uniform hypergraphs or
$k$
-uniform hypergraphs or
![]() $k$
-graphs for short. A
$k$
-graphs for short. A
![]() $k$
-graph
$k$
-graph
![]() $\mathcal{F}$
is called
$\mathcal{F}$
is called
![]() $t$
-intersecting if
$t$
-intersecting if
![]() $|F\cap F'|\geq t$
for all
$|F\cap F'|\geq t$
for all
![]() $F,F'\in{\mathcal{F}}$
. In case of
$F,F'\in{\mathcal{F}}$
. In case of
![]() $t=1$
we often use the term intersecting instead of 1-intersecting. Investigating various properties of
$t=1$
we often use the term intersecting instead of 1-intersecting. Investigating various properties of
![]() $t$
-intersecting families is one of the central topics of extremal set theory (cf. the recent book of Gerbner and Patkós [Reference Gerbner and Patkós13]). Let us state the quintessential result of this topic.
$t$
-intersecting families is one of the central topics of extremal set theory (cf. the recent book of Gerbner and Patkós [Reference Gerbner and Patkós13]). Let us state the quintessential result of this topic.
Erdős-Ko-Rado Theorem ([Reference Erdős, Ko and Rado3]). Suppose that
![]() $n\geq n_0(k,t)$
and
$n\geq n_0(k,t)$
and
![]() ${\mathcal{F}}\subset \binom{[n]}{k}$
is
${\mathcal{F}}\subset \binom{[n]}{k}$
is
![]() $t$
-intersecting. Then
$t$
-intersecting. Then
Remark 1. For
![]() $t=1$
the exact value
$t=1$
the exact value
![]() $n_0(k,t)=(k-t+1)(t+1)$
was proved in [Reference Erdős, Ko and Rado3]. For
$n_0(k,t)=(k-t+1)(t+1)$
was proved in [Reference Erdős, Ko and Rado3]. For
![]() $t\geq 15$
it is due to [Reference Frankl5]. Finally Wilson [Reference Wilson21] closed the gap
$t\geq 15$
it is due to [Reference Frankl5]. Finally Wilson [Reference Wilson21] closed the gap
![]() $2\leq t\leq 14$
with a proof valid for all
$2\leq t\leq 14$
with a proof valid for all
![]() $t$
.
$t$
.
Let us note that the full t-star,
![]() $\left \{F\in \binom{[n]}{k}\colon [t]\subset F\right \}$
shows that (1) is best possible. In general, for a set
$\left \{F\in \binom{[n]}{k}\colon [t]\subset F\right \}$
shows that (1) is best possible. In general, for a set
![]() $T\subset [n]$
let
$T\subset [n]$
let
![]() ${\mathcal{S}}_T=\left \{S\in \binom{[n]}{k}\colon T\subset S\right \}$
denote the star of T.
${\mathcal{S}}_T=\left \{S\in \binom{[n]}{k}\colon T\subset S\right \}$
denote the star of T.
For
![]() $t=1$
, there is a strong stability for the Erdős-Ko-Rado Theorem.
$t=1$
, there is a strong stability for the Erdős-Ko-Rado Theorem.
Theorem 1.1 (Hilton-Milner Theorem [Reference Hilton and Milner14]). Suppose that
![]() $n\gt 2k\geq 4$
,
$n\gt 2k\geq 4$
,
![]() ${\mathcal{F}}\subset \binom{[n]}{k}$
is intersecting and
${\mathcal{F}}\subset \binom{[n]}{k}$
is intersecting and
![]() $\mathcal{F}$
is not a star, then
$\mathcal{F}$
is not a star, then
Let us define the Hilton-Milner Family
showing that (2) is best possible.
Let us recall the notion of immediate shadow,
![]() $\partial{\mathcal{F}}$
: For
$\partial{\mathcal{F}}$
: For
![]() ${\mathcal{F}}\subset \binom{[n]}{k}$
,
${\mathcal{F}}\subset \binom{[n]}{k}$
,
If for some
![]() $G\in \partial{\mathcal{F}}$
there is only one choice of
$G\in \partial{\mathcal{F}}$
there is only one choice of
![]() $F\in{\mathcal{F}}$
satisfying
$F\in{\mathcal{F}}$
satisfying
![]() $G\subset F$
then
$G\subset F$
then
![]() $G$
is called unique or a unique shadow. Note that in the full star
$G$
is called unique or a unique shadow. Note that in the full star
![]() ${\mathcal{S}}_{\{x\}}$
for each member
${\mathcal{S}}_{\{x\}}$
for each member
![]() $S$
,
$S$
,
![]() $S\setminus \{x\}$
is unique. In the Hilton-Milner family
$S\setminus \{x\}$
is unique. In the Hilton-Milner family
![]() ${\mathcal{H}}(n,k)$
, each member
${\mathcal{H}}(n,k)$
, each member
![]() $H\in{\mathcal{H}}(n,k)\setminus \{[2,k+1]\}$
contains a unique shadow
$H\in{\mathcal{H}}(n,k)\setminus \{[2,k+1]\}$
contains a unique shadow
![]() $H\setminus \{1\}$
. Just for curiosity let us mention that if each member of
$H\setminus \{1\}$
. Just for curiosity let us mention that if each member of
![]() ${\mathcal{F}}\subset \binom{[n]}{k}$
contains a unique shadow then
${\mathcal{F}}\subset \binom{[n]}{k}$
contains a unique shadow then
![]() $|{\mathcal{F}}|\leq \binom{n-1}{k-1}$
.
$|{\mathcal{F}}|\leq \binom{n-1}{k-1}$
.
Let us introduce the central notion of the present paper.
Definition 1.2. For an integer
![]() $r\geq 2$
and a family
$r\geq 2$
and a family
![]() ${\mathcal{F}}\subset \binom{[n]}{k}$
, we say that
${\mathcal{F}}\subset \binom{[n]}{k}$
, we say that
![]() $\mathcal{F}$
is
$\mathcal{F}$
is
![]() $r$
-complete if every
$r$
-complete if every
![]() $G\in \partial{\mathcal{F}}$
is contained in at least
$G\in \partial{\mathcal{F}}$
is contained in at least
![]() $r$
members of
$r$
members of
![]() $\mathcal{F}$
.
$\mathcal{F}$
.
Note that
![]() $\mathcal{F}$
is
$\mathcal{F}$
is
![]() $r$
-complete if and only if the minimum non-zero co-degree of
$r$
-complete if and only if the minimum non-zero co-degree of
![]() $\mathcal{F}$
is at least
$\mathcal{F}$
is at least
![]() $r$
. This notion has been introduced and used by Kostochka et al. [Reference Kostochka, Mubayi and Verstraëte17–Reference Kostochka, Mubayi and Verstraëte19] to determine hypergraph Turán numbers for paths, cycles and trees.
$r$
. This notion has been introduced and used by Kostochka et al. [Reference Kostochka, Mubayi and Verstraëte17–Reference Kostochka, Mubayi and Verstraëte19] to determine hypergraph Turán numbers for paths, cycles and trees.
Clearly, if
![]() ${\mathcal{F}}\subset \binom{[n]}{k}$
is
${\mathcal{F}}\subset \binom{[n]}{k}$
is
![]() $r$
-complete with
$r$
-complete with
![]() $r\geq 2$
, then
$r\geq 2$
, then
![]() $\mathcal{F}$
is far from a star. It is natural to ask for the maximum size of an
$\mathcal{F}$
is far from a star. It is natural to ask for the maximum size of an
![]() $r$
-complete intersecting family. Let us define the function:
$r$
-complete intersecting family. Let us define the function:
Let us give some examples. For
![]() $1\leq r\lt k$
the complete
$1\leq r\lt k$
the complete
![]() $k$
-graph
$k$
-graph
![]() $\binom{[k+r]}{k}$
is intersecting and
$\binom{[k+r]}{k}$
is intersecting and
![]() $(r+1)$
-complete. This shows in particular that
$(r+1)$
-complete. This shows in particular that
Example 1.3. For
![]() $n\geq k\geq r\geq 1$
define
$n\geq k\geq r\geq 1$
define
Clearly
![]() ${\mathcal{L}}(n,k,r)$
is intersecting,
${\mathcal{L}}(n,k,r)$
is intersecting,
![]() $r$
-complete and
$r$
-complete and
Our main result shows that this example is best possible for
![]() $n\geq n_0(k,r)$
.
$n\geq n_0(k,r)$
.
Theorem 1.4.
For
![]() $n\geq 28k$
,
$n\geq 28k$
,
Moreover, up to isomorphism
![]() ${\mathcal{L}}(n,k,2)$
is the only family attaining equality.
${\mathcal{L}}(n,k,2)$
is the only family attaining equality.
Theorem 1.5.
For
![]() $k\geq 3$
,
$k\geq 3$
,
![]() $r\geq 3$
and
$r\geq 3$
and
![]() $n\geq n_0(k,r)$
,
$n\geq n_0(k,r)$
,
 \begin{align} f(n,k,r) = \left \{\begin{array}{l@{\quad}l} |{\mathcal{L}}(n,k,r)|,& 3\leq r\leq k;\\[5pt] 0. &r\geq k+1. \end{array}\right . \end{align}
\begin{align} f(n,k,r) = \left \{\begin{array}{l@{\quad}l} |{\mathcal{L}}(n,k,r)|,& 3\leq r\leq k;\\[5pt] 0. &r\geq k+1. \end{array}\right . \end{align}
For a positive integer
![]() $\ell$
and an
$\ell$
and an
![]() $\ell$
-graph
$\ell$
-graph
![]() $\mathcal{H}$
, define the clique family
$\mathcal{H}$
, define the clique family
Define
![]() $\nu ({\mathcal{F}})$
, the matching number of
$\nu ({\mathcal{F}})$
, the matching number of
![]() $\mathcal{F}$
as the maximum number of pairwise disjoint edges in
$\mathcal{F}$
as the maximum number of pairwise disjoint edges in
![]() $\mathcal{F}$
. Note that
$\mathcal{F}$
. Note that
![]() $\nu ({\mathcal{F}})=1$
iff
$\nu ({\mathcal{F}})=1$
iff
![]() $\mathcal{F}$
is intersecting. We are going to prove Theorem 1.4 using the following result exhibiting a surprising connection between the matching number and the size of the clique family. Define the Erdős-family
$\mathcal{F}$
is intersecting. We are going to prove Theorem 1.4 using the following result exhibiting a surprising connection between the matching number and the size of the clique family. Define the Erdős-family
Note that
Theorem 1.6.
Let
![]() ${\mathcal{F}}\subset \binom{[n]}{k}$
be a family with
${\mathcal{F}}\subset \binom{[n]}{k}$
be a family with
![]() $\nu ({\mathcal{F}})\leq s$
. If
$\nu ({\mathcal{F}})\leq s$
. If
![]() $n\geq 5sk+13k$
and
$n\geq 5sk+13k$
and
![]() $s\geq 3$
, then
$s\geq 3$
, then
Moreover, up to isomorphism
![]() ${\mathcal{E}}(n,k,s)$
is the only family attaining equality.
${\mathcal{E}}(n,k,s)$
is the only family attaining equality.
Let us define the notion of
![]() $r$
-complete edges.
$r$
-complete edges.
Definition 1.7. For an integer
![]() $r\geq 2$
and a family
$r\geq 2$
and a family
![]() ${\mathcal{F}}\subset \binom{[n]}{k}$
, we say that
${\mathcal{F}}\subset \binom{[n]}{k}$
, we say that
![]() $F\in{\mathcal{F}}$
is
$F\in{\mathcal{F}}$
is
![]() $r$
-complete if every
$r$
-complete if every
![]() $G\in \binom{F}{k-1}$
is contained in at least
$G\in \binom{F}{k-1}$
is contained in at least
![]() $r$
members of
$r$
members of
![]() $\mathcal{F}$
.
$\mathcal{F}$
.
Clearly,
![]() $\mathcal{F}$
is
$\mathcal{F}$
is
![]() $r$
-complete if and only if every
$r$
-complete if and only if every
![]() $F\in{\mathcal{F}}$
is
$F\in{\mathcal{F}}$
is
![]() $r$
-complete. One can also ask for the maximum number of
$r$
-complete. One can also ask for the maximum number of
![]() $r$
-complete edges in an intersecting family. For an intersecting family
$r$
-complete edges in an intersecting family. For an intersecting family
![]() ${\mathcal{F}}\subset \binom{[n]}{k}$
, define
${\mathcal{F}}\subset \binom{[n]}{k}$
, define
![]() ${\mathcal{F}}^*_r({\mathcal{F}})$
as the family of all
${\mathcal{F}}^*_r({\mathcal{F}})$
as the family of all
![]() $r$
-complete edges in
$r$
-complete edges in
![]() $\mathcal{F}$
. Let
$\mathcal{F}$
. Let
If
![]() $\mathcal{F}$
is
$\mathcal{F}$
is
![]() $r$
-complete then we have
$r$
-complete then we have
![]() ${\mathcal{F}}^*_r({\mathcal{F}})={\mathcal{F}}$
, implying that
${\mathcal{F}}^*_r({\mathcal{F}})={\mathcal{F}}$
, implying that
![]() $f(n,k,r)\leq f^*(n,k,r)$
. For
$f(n,k,r)\leq f^*(n,k,r)$
. For
![]() ${\mathcal{F}}'\subset{\mathcal{F}}$
, we say that
${\mathcal{F}}'\subset{\mathcal{F}}$
, we say that
![]() ${\mathcal{F}}'$
is relatively
${\mathcal{F}}'$
is relatively
![]() $r$
-complete with respect to
$r$
-complete with respect to
![]() $\mathcal{F}$
if every
$\mathcal{F}$
if every
![]() $F'\in{\mathcal{F}}'$
is an
$F'\in{\mathcal{F}}'$
is an
![]() $r$
-complete edge in
$r$
-complete edge in
![]() $\mathcal{F}$
. Clearly
$\mathcal{F}$
. Clearly
![]() ${\mathcal{F}}^*_r({\mathcal{F}})$
is a relatively
${\mathcal{F}}^*_r({\mathcal{F}})$
is a relatively
![]() $r$
-complete family of the maximum size with respect to
$r$
-complete family of the maximum size with respect to
![]() $\mathcal{F}$
.
$\mathcal{F}$
.
Our next result determines
![]() $f^*(n,k,r)$
for all
$f^*(n,k,r)$
for all
![]() $k\geq 3$
and
$k\geq 3$
and
![]() $r\geq 2$
, asymptotically.
$r\geq 2$
, asymptotically.
Theorem 1.8.
For
![]() $k\geq 3$
,
$k\geq 3$
,
![]() $r\geq 2$
and
$r\geq 2$
and
![]() $n\geq n_0(k,r)$
,
$n\geq n_0(k,r)$
,
 \begin{align} f^*(n,k,r) = \left \{\begin{array}{l@{\quad}l} |{\mathcal{L}}(n,k,r)|,&r=2,3;\\[5pt] \binom{n-3}{k-3}+O(n^{k-r}), &4\leq r\leq k-1;\\[5pt] \binom{n-3}{k-3},& r\geq k\geq 4. \end{array}\right . \end{align}
\begin{align} f^*(n,k,r) = \left \{\begin{array}{l@{\quad}l} |{\mathcal{L}}(n,k,r)|,&r=2,3;\\[5pt] \binom{n-3}{k-3}+O(n^{k-r}), &4\leq r\leq k-1;\\[5pt] \binom{n-3}{k-3},& r\geq k\geq 4. \end{array}\right . \end{align}
The next proposition shows that the term
![]() $O(n^{k-r})$
in (6) cannot be removed for
$O(n^{k-r})$
in (6) cannot be removed for
![]() $k\geq 5$
and
$k\geq 5$
and
![]() $4\leq r\leq k-1$
.
$4\leq r\leq k-1$
.
Proposition 1.9.
For
![]() $k\geq 5$
,
$k\geq 5$
,
![]() $4\leq r\leq k-1$
and
$4\leq r\leq k-1$
and
![]() $n\geq k+r-1$
,
$n\geq k+r-1$
,
Proof. For
![]() $4\leq r\leq k-1$
, let
$4\leq r\leq k-1$
, let
and let
It is easy to check that
![]() $B(r)$
is intersecting, implying that
$B(r)$
is intersecting, implying that
![]() ${\mathcal{I}}(n,k,r)$
is intersecting. Since
${\mathcal{I}}(n,k,r)$
is intersecting. Since
![]() ${\mathcal{S}}_{\{1,2,3\}}\subset{\mathcal{S}}_{\{1,2\}}$
and
${\mathcal{S}}_{\{1,2,3\}}\subset{\mathcal{S}}_{\{1,2\}}$
and
![]() ${\mathcal{S}}_{[r+2]\setminus \{3\}}\subset{\mathcal{S}}_{\{1,2\}}$
,
${\mathcal{S}}_{[r+2]\setminus \{3\}}\subset{\mathcal{S}}_{\{1,2\}}$
,
![]() ${\mathcal{I}}^*(n,k,r)\subset{\mathcal{I}}(n,k,r)$
. In the rest of the proof, we show that
${\mathcal{I}}^*(n,k,r)\subset{\mathcal{I}}(n,k,r)$
. In the rest of the proof, we show that
![]() ${\mathcal{I}}^*(n,k,r)$
is relatively
${\mathcal{I}}^*(n,k,r)$
is relatively
![]() $r$
-complete with respect to
$r$
-complete with respect to
![]() ${\mathcal{I}}(n,k,r)$
.
${\mathcal{I}}(n,k,r)$
.
For any
![]() $F\in{\mathcal{S}}_{\{1,2,3\}}$
, since
$F\in{\mathcal{S}}_{\{1,2,3\}}$
, since
![]() $\mathcal{S}_{\{1,2\}}\subset{\mathcal{I}}(n,k,r)$
and
$\mathcal{S}_{\{1,2\}}\subset{\mathcal{I}}(n,k,r)$
and
![]() $n\geq k+r-1$
, we see that for each
$n\geq k+r-1$
, we see that for each
![]() $x\in F\setminus \{1,2\}$
,
$x\in F\setminus \{1,2\}$
,
![]() $F\setminus \{x\}$
is covered by at least
$F\setminus \{x\}$
is covered by at least
![]() $r$
members of
$r$
members of
![]() ${\mathcal{I}}(n,k,r)$
. Moreover, since
${\mathcal{I}}(n,k,r)$
. Moreover, since
![]() $\mathcal{S}_{\{3,i,j\}}\subset{\mathcal{I}}(n,k,r)$
for
$\mathcal{S}_{\{3,i,j\}}\subset{\mathcal{I}}(n,k,r)$
for
![]() $i\in \{1,2\}$
and
$i\in \{1,2\}$
and
![]() $j\in \{4,5,\ldots, r+2\}$
, we infer that
$j\in \{4,5,\ldots, r+2\}$
, we infer that
![]() $F\setminus \{3-i\}$
is covered by at least
$F\setminus \{3-i\}$
is covered by at least
![]() $r$
members of
$r$
members of
![]() ${\mathcal{I}}(n,k,r)$
for
${\mathcal{I}}(n,k,r)$
for
![]() $i=1,2$
. Thus
$i=1,2$
. Thus
![]() ${\mathcal{S}}_{\{1,2,3\}}$
is relatively
${\mathcal{S}}_{\{1,2,3\}}$
is relatively
![]() $r$
-complete with respect to
$r$
-complete with respect to
![]() ${\mathcal{I}}(n,k,r)$
.
${\mathcal{I}}(n,k,r)$
.
Let
![]() $F\in{\mathcal{S}}_{[r+2]\setminus \{3\}}$
and
$F\in{\mathcal{S}}_{[r+2]\setminus \{3\}}$
and
![]() $G\in \binom{F}{k-1}$
. If
$G\in \binom{F}{k-1}$
. If
![]() $\{1,2\}\subset G$
, then by
$\{1,2\}\subset G$
, then by
![]() $\mathcal{S}_{\{1,2\}}\subset{\mathcal{I}}(n,k,r)$
and
$\mathcal{S}_{\{1,2\}}\subset{\mathcal{I}}(n,k,r)$
and
![]() $n\geq k+r$
we infer that
$n\geq k+r$
we infer that
![]() $G$
is covered by at least
$G$
is covered by at least
![]() $r$
members of
$r$
members of
![]() ${\mathcal{I}}(n,k,r)$
. If
${\mathcal{I}}(n,k,r)$
. If
![]() $i\notin G$
for
$i\notin G$
for
![]() $i=1,2$
, since
$i=1,2$
, since
![]() ${\mathcal{S}}_{[r+2]\setminus \{i,3\}}\subset{\mathcal{I}}(n,k,r)$
and
${\mathcal{S}}_{[r+2]\setminus \{i,3\}}\subset{\mathcal{I}}(n,k,r)$
and
![]() $n\geq k+r-1$
, then
$n\geq k+r-1$
, then
![]() $G$
is also covered by at least
$G$
is also covered by at least
![]() $r$
members of
$r$
members of
![]() ${\mathcal{I}}(n,k,r)$
. Hence
${\mathcal{I}}(n,k,r)$
. Hence
![]() ${\mathcal{S}}_{[r+2]\setminus \{3\}}$
is relatively
${\mathcal{S}}_{[r+2]\setminus \{3\}}$
is relatively
![]() $r$
-complete with respect to
$r$
-complete with respect to
![]() ${\mathcal{I}}(n,k,r)$
. Therefore,
${\mathcal{I}}(n,k,r)$
. Therefore,
![]() ${\mathcal{I}}^*(n,k,r)$
is relatively
${\mathcal{I}}^*(n,k,r)$
is relatively
![]() $r$
-complete with respect to
$r$
-complete with respect to
![]() ${\mathcal{I}}(n,k,r)$
and
${\mathcal{I}}(n,k,r)$
and
The rest of the paper is organized as follows. We list some results that are needed in Section 2. We prove Theorems 1.4 and 1.6 in Section 3 and prove Theorem 1.5 in Section 4. The proof of Theorem 1.8 splits into two parts. In Section 5, we prove it for
![]() $3\leq r\lt k$
. In Section 6, we prove it for
$3\leq r\lt k$
. In Section 6, we prove it for
![]() $r\geq k$
. Finally, we give some concluding remarks in Section 7.
$r\geq k$
. Finally, we give some concluding remarks in Section 7.
2. Preliminaries
In this section, we list some notions and results that are needed for the proofs.
For a family
![]() ${\mathcal{F}}\subset \binom{[n]}{k}$
define the family of transversals,
${\mathcal{F}}\subset \binom{[n]}{k}$
define the family of transversals,
![]() ${\mathcal{T}}({\mathcal{F}})$
by
${\mathcal{T}}({\mathcal{F}})$
by
Note that
![]() $\mathcal{F}$
is intersecting iff
$\mathcal{F}$
is intersecting iff
![]() ${\mathcal{F}}\subset{\mathcal{T}}({\mathcal{F}})$
. Note also that
${\mathcal{F}}\subset{\mathcal{T}}({\mathcal{F}})$
. Note also that
![]() ${\mathcal{T}}({\mathcal{F}})$
is not uniform in general. Set
${\mathcal{T}}({\mathcal{F}})$
is not uniform in general. Set
![]() ${\mathcal{T}}^{(k)}({\mathcal{F}}) = \{T\in{\mathcal{T}}({\mathcal{F}})\colon |T|=k\}$
. If
${\mathcal{T}}^{(k)}({\mathcal{F}}) = \{T\in{\mathcal{T}}({\mathcal{F}})\colon |T|=k\}$
. If
![]() ${\mathcal{F}}={\mathcal{T}}^{(k)}({\mathcal{F}})$
then
${\mathcal{F}}={\mathcal{T}}^{(k)}({\mathcal{F}})$
then
![]() $\mathcal{F}$
is called saturated. It is equivalent to the fact that
$\mathcal{F}$
is called saturated. It is equivalent to the fact that
![]() ${\mathcal{F}}\cup \{H\}$
is no longer intersecting for
${\mathcal{F}}\cup \{H\}$
is no longer intersecting for
![]() $H\in \binom{[n]}{k}\setminus{\mathcal{F}}$
. It should be clear that in the definition of
$H\in \binom{[n]}{k}\setminus{\mathcal{F}}$
. It should be clear that in the definition of
![]() $f^*(n,k,r)$
it is sufficient to consider saturated intersecting families
$f^*(n,k,r)$
it is sufficient to consider saturated intersecting families
![]() $\mathcal{F}$
.
$\mathcal{F}$
.
Let us recall a special case of the Katona Intersecting Shadow Theorem [Reference Katona15].
Theorem 2.1 ([Reference Katona15]). Suppose that
![]() ${\mathcal{F}}\subset \binom{[n]}{k}$
is intersecting. Then
${\mathcal{F}}\subset \binom{[n]}{k}$
is intersecting. Then
We need the following generalization of (7) as well.
Theorem 2.2 ([Reference Frankl8]). Suppose that
![]() ${\mathcal{F}}\subset \binom{[n]}{k}$
. Then
${\mathcal{F}}\subset \binom{[n]}{k}$
. Then
We need also a classical result of Bollobás, the so-called Bollobás Set-pair Inequality.
Theorem 2.3 ([Reference Bollobás1]). Let
![]() $a,b$
be positive integers,
$a,b$
be positive integers,
![]() $A_1,\ldots,A_m$
$A_1,\ldots,A_m$
![]() $a$
-element sets,
$a$
-element sets,
![]() $B_1,\ldots,B_m$
$B_1,\ldots,B_m$
![]() $b$
-element sets such that
$b$
-element sets such that
![]() $A_i\cap B_j=\emptyset$
iff
$A_i\cap B_j=\emptyset$
iff
![]() $i=j$
. Then
$i=j$
. Then

There is a very important operation on families of sets which was discovered by Erdős et al. [Reference Erdős, Ko and Rado3]. It is called shifting and it is known not to increase the matching number
![]() $\nu ({\mathcal{F}})$
([Reference Frankl7]) and not to decrease the size of
$\nu ({\mathcal{F}})$
([Reference Frankl7]) and not to decrease the size of
![]() ${\mathcal{K}}({\mathcal{F}})$
(cf. [Reference Liu and Wang20]).
${\mathcal{K}}({\mathcal{F}})$
(cf. [Reference Liu and Wang20]).
Let us define the shifting partial order
![]() $\prec$
. For two
$\prec$
. For two
![]() $k$
-sets
$k$
-sets
![]() $A$
and
$A$
and
![]() $B$
where
$B$
where
![]() $A=\{a_1,\ldots,a_k\}$
,
$A=\{a_1,\ldots,a_k\}$
,
![]() $a_1\lt \ldots \lt a_k$
and
$a_1\lt \ldots \lt a_k$
and
![]() $B=\{b_1,\ldots,b_k\}$
,
$B=\{b_1,\ldots,b_k\}$
,
![]() $b_1\lt \ldots \lt b_k$
we say that
$b_1\lt \ldots \lt b_k$
we say that
![]() $A$
precedes
$A$
precedes
![]() $B$
and denote it by
$B$
and denote it by
![]() $A\prec B$
if
$A\prec B$
if
![]() $a_i\leq b_i$
for all
$a_i\leq b_i$
for all
![]() $1\leq i\leq k$
.
$1\leq i\leq k$
.
A family
![]() ${\mathcal{F}}\subset \binom{[n]}{k}$
is called shifted (or initial) if
${\mathcal{F}}\subset \binom{[n]}{k}$
is called shifted (or initial) if
![]() $A\prec B$
and
$A\prec B$
and
![]() $B\in{\mathcal{F}}$
always imply
$B\in{\mathcal{F}}$
always imply
![]() $A\in{\mathcal{F}}$
. By repeated shifting one can transform an arbitrary
$A\in{\mathcal{F}}$
. By repeated shifting one can transform an arbitrary
![]() $k$
-graph into a shifted
$k$
-graph into a shifted
![]() $k$
-graph with the same number of edges.
$k$
-graph with the same number of edges.
We need the following inequality generalizing the case
![]() $t=1$
of the Erdős-Ko-Rado Theorem.
$t=1$
of the Erdős-Ko-Rado Theorem.
Proposition 2.4 ([Reference Frankl7]). Suppose that
![]() ${\mathcal{F}}\subset \binom{[n]}{k}$
then
${\mathcal{F}}\subset \binom{[n]}{k}$
then
Finally we need the following stability theorem concerning the Erdős-Ko-Rado Theorem.
Hilton-Milner-Frankl Theorem ([Reference Frankl6,Reference Hilton and Milner14]). Suppose that
![]() ${\mathcal{F}}\subset \binom{[n]}{k}$
is
${\mathcal{F}}\subset \binom{[n]}{k}$
is
![]() $t$
-intersecting,
$t$
-intersecting,
![]() $\mathcal{F}$
is not a
$\mathcal{F}$
is not a
![]() $t$
-star and
$t$
-star and
![]() $n\geq (k-t+1)(t+1)$
. Then
$n\geq (k-t+1)(t+1)$
. Then
3. Intersecting families without unique shadow
In this section, we first prove Theorem 1.4 by assuming Theorem 1.6. Then by using the decomposition method of a shifted family introduced in [Reference Frankl9], we give a proof of Theorem 1.6.
Actually, we shall prove the following version of Theorem 1.4, which also gives the
![]() $r=2$
case of Theorem 1.8.
$r=2$
case of Theorem 1.8.
Theorem 3.1.
For
![]() $n\geq 28k$
,
$n\geq 28k$
,
Moreover, up to isomorphism
![]() ${\mathcal{L}}(n,k,2)$
is the only family attaining equality.
${\mathcal{L}}(n,k,2)$
is the only family attaining equality.
Proof of Theorem
1.4. Recall that
![]() ${\mathcal{L}}(n,k,2)$
is 2-complete intersecting and
${\mathcal{L}}(n,k,2)$
is 2-complete intersecting and
![]() $f(n,k,2)\leq f^*(n,k,2)$
. It follows that
$f(n,k,2)\leq f^*(n,k,2)$
. It follows that
![]() $|{\mathcal{L}}(n,k,2)|\leq f(n,k,2)\leq f^*(n,k,2)$
. Thus we are left to show
$|{\mathcal{L}}(n,k,2)|\leq f(n,k,2)\leq f^*(n,k,2)$
. Thus we are left to show
![]() $f^*(n,k,2)\leq |{\mathcal{L}}(n,k,2)|$
.
$f^*(n,k,2)\leq |{\mathcal{L}}(n,k,2)|$
.
Let
![]() ${\mathcal{F}}\subset \binom{[n]}{k}$
be an intersecting family. Let
${\mathcal{F}}\subset \binom{[n]}{k}$
be an intersecting family. Let
![]() ${\mathcal{F}}^*$
be the family of 2-complete sets in
${\mathcal{F}}^*$
be the family of 2-complete sets in
![]() $\mathcal{F}$
and let
$\mathcal{F}$
and let
![]() ${\mathcal{H}}=\partial{{\mathcal{F}}^*}$
. Note that this guarantees that every member of
${\mathcal{H}}=\partial{{\mathcal{F}}^*}$
. Note that this guarantees that every member of
![]() $\mathcal{H}$
is contained in at least two members of
$\mathcal{H}$
is contained in at least two members of
![]() $\mathcal{F}$
.
$\mathcal{F}$
.
Claim 1.
![]() $\nu ({\mathcal{H}})\leq 3$
.
$\nu ({\mathcal{H}})\leq 3$
.
Proof. Suppose for contradiction that
![]() $D_i=F_i\cap G_i$
,
$D_i=F_i\cap G_i$
,
![]() $1\leq i\leq 4$
, are pairwise disjoint sets in
$1\leq i\leq 4$
, are pairwise disjoint sets in
![]() $\mathcal{H}$
and
$\mathcal{H}$
and
![]() $F_i,G_i\in{\mathcal{F}}$
. Define
$F_i,G_i\in{\mathcal{F}}$
. Define
![]() $x_i,y_i$
by
$x_i,y_i$
by
![]() $F_i\setminus D_i =\{x_i\}$
,
$F_i\setminus D_i =\{x_i\}$
,
![]() $G_i\setminus D_i =\{y_i\}$
. Since
$G_i\setminus D_i =\{y_i\}$
. Since
![]() $|\{x_i,y_i\}|=2$
, by symmetry we may assume that
$|\{x_i,y_i\}|=2$
, by symmetry we may assume that
![]() $(x_1,y_1)\cap D_4= \emptyset$
. This implies
$(x_1,y_1)\cap D_4= \emptyset$
. This implies
![]() $F_1\cap D_4=\emptyset, G_1\cap D_4=\emptyset$
. From
$F_1\cap D_4=\emptyset, G_1\cap D_4=\emptyset$
. From
![]() $F_4\cap F_1\neq \emptyset$
,
$F_4\cap F_1\neq \emptyset$
,
![]() $F_4\cap G_1\neq \emptyset$
,
$F_4\cap G_1\neq \emptyset$
,
![]() $G_4\cap F_1\neq \emptyset$
and
$G_4\cap F_1\neq \emptyset$
and
![]() $G_4\cap G_1\neq \emptyset$
, we infer
$G_4\cap G_1\neq \emptyset$
, we infer
![]() $(x_4,y_4)\subset D_1$
. Consequently
$(x_4,y_4)\subset D_1$
. Consequently
![]() $F_4\cap D_p=\emptyset$
,
$F_4\cap D_p=\emptyset$
,
![]() $G_4\cap D_p=\emptyset$
for
$G_4\cap D_p=\emptyset$
for
![]() $p=2,3$
. This implies as above
$p=2,3$
. This implies as above
![]() $(x_p,y_p)\subset D_4$
. Now
$(x_p,y_p)\subset D_4$
. Now
![]() $x_2\neq x_3$
or
$x_2\neq x_3$
or
![]() $x_2\neq y_3$
(or both) hold. By symmetry
$x_2\neq y_3$
(or both) hold. By symmetry
![]() $x_2\neq x_3$
. Then
$x_2\neq x_3$
. Then
![]() $F_2\cap F_3=\emptyset$
, a contradiction.
$F_2\cap F_3=\emptyset$
, a contradiction.
By Theorem 1.6 and Claim 1, for
![]() $n\geq (5\times 3+13)k=28k$
we have
$n\geq (5\times 3+13)k=28k$
we have
![]() $|{\mathcal{F}}^*|\leq |{\mathcal{K}}({\mathcal{H}})|\leq |{\mathcal{K}}({\mathcal{E}}(n,k,3))|=|{\mathcal{L}}(n,k,2)|$
. The uniqueness follows from Theorem 1.6.
$|{\mathcal{F}}^*|\leq |{\mathcal{K}}({\mathcal{H}})|\leq |{\mathcal{K}}({\mathcal{E}}(n,k,3))|=|{\mathcal{L}}(n,k,2)|$
. The uniqueness follows from Theorem 1.6.
The families
![]() ${\mathcal{F}}_0,{\mathcal{F}}_1, \ldots,{\mathcal{F}}_s$
are called overlapping if there is no choice of
${\mathcal{F}}_0,{\mathcal{F}}_1, \ldots,{\mathcal{F}}_s$
are called overlapping if there is no choice of
![]() $F_i \in{\mathcal{F}}_i$
such that
$F_i \in{\mathcal{F}}_i$
such that
![]() $F_0, F_1, \ldots, F_s$
are pairwise disjoint. For the proof of Theorem 1.6 the following lemma is needed. A similar lemma was proved in [Reference Frankl and Wang11], although without characterization of the case of equality.
$F_0, F_1, \ldots, F_s$
are pairwise disjoint. For the proof of Theorem 1.6 the following lemma is needed. A similar lemma was proved in [Reference Frankl and Wang11], although without characterization of the case of equality.
Lemma 3.2.
Let
![]() ${\mathcal{F}}_{0}\subset{\mathcal{F}}_{1}\subset \cdots \subset{\mathcal{F}}_{s}\subset \binom{Y}{\ell }$
be overlapping families and let
${\mathcal{F}}_{0}\subset{\mathcal{F}}_{1}\subset \cdots \subset{\mathcal{F}}_{s}\subset \binom{Y}{\ell }$
be overlapping families and let
![]() $p_0\geq p_1\geq \ldots \geq p_s$
be positive reals. Let
$p_0\geq p_1\geq \ldots \geq p_s$
be positive reals. Let
For
![]() $|Y|\geq (d_{\vec{p}}+1) \ell$
,
$|Y|\geq (d_{\vec{p}}+1) \ell$
,
where the equality holds iff
![]() ${\mathcal{F}}_{1}= \cdots ={\mathcal{F}}_{s}=\binom{Y}{\ell }$
,
${\mathcal{F}}_{1}= \cdots ={\mathcal{F}}_{s}=\binom{Y}{\ell }$
,
![]() ${\mathcal{F}}_0=\emptyset$
.
${\mathcal{F}}_0=\emptyset$
.
Proof. Let
![]() ${\mathcal{F}}_0\subset{\mathcal{F}}_1\subset \cdots \subset{\mathcal{F}}_s\subset \binom{Y}{\ell }$
be overlapping families. Let
${\mathcal{F}}_0\subset{\mathcal{F}}_1\subset \cdots \subset{\mathcal{F}}_s\subset \binom{Y}{\ell }$
be overlapping families. Let
![]() $ t = \lfloor |Y|/\ell \rfloor \geq\lfloor d_{\vec{p}}\rfloor +1\geq s+1$
and choose a random matching
$ t = \lfloor |Y|/\ell \rfloor \geq\lfloor d_{\vec{p}}\rfloor +1\geq s+1$
and choose a random matching
![]() $F_1,F_2,\ldots,F_t$
from
$F_1,F_2,\ldots,F_t$
from
![]() $\binom{Y}{\ell }$
. Consider the weighted bipartite graph
$\binom{Y}{\ell }$
. Consider the weighted bipartite graph
![]() $G$
on partite sets
$G$
on partite sets
![]() $\{F_1,F_2,\ldots,F_t\}$
and
$\{F_1,F_2,\ldots,F_t\}$
and
![]() $\{{\mathcal{F}}_0,{\mathcal{F}}_1, \cdots,{\mathcal{F}}_s\}$
where we have an edge
$\{{\mathcal{F}}_0,{\mathcal{F}}_1, \cdots,{\mathcal{F}}_s\}$
where we have an edge
![]() $(F_i,{\mathcal{F}}_j)$
iff
$(F_i,{\mathcal{F}}_j)$
iff
![]() $F_i\in{\mathcal{F}}_j$
. This edge gets weight
$F_i\in{\mathcal{F}}_j$
. This edge gets weight
![]() $p_j$
.
$p_j$
.
Since
![]() ${\mathcal{F}}_{0}\subset{\mathcal{F}}_{1}\subset \cdots \subset{\mathcal{F}}_{s}$
are overlapping,
${\mathcal{F}}_{0}\subset{\mathcal{F}}_{1}\subset \cdots \subset{\mathcal{F}}_{s}$
are overlapping,
![]() $G$
has matching number at most
$G$
has matching number at most
![]() $s$
. Applying the König-Hall Theorem we can find
$s$
. Applying the König-Hall Theorem we can find
![]() $s$
vertices covering all edges of the bipartite graph
$s$
vertices covering all edges of the bipartite graph
![]() $G$
. Let
$G$
. Let
![]() $F_1,\ldots,F_q$
be the vertices of the covering set chosen from the random matching and
$F_1,\ldots,F_q$
be the vertices of the covering set chosen from the random matching and
![]() ${\mathcal{F}}_{q+1}, \ldots,{\mathcal{F}}_s$
the remaining
${\mathcal{F}}_{q+1}, \ldots,{\mathcal{F}}_s$
the remaining
![]() $s-q$
chosen from the families.
$s-q$
chosen from the families.
The total weight of the edges covered by
![]() $F_i$
is at most
$F_i$
is at most
![]() $p_0+\ldots +p_s$
. The total weight of the edges covered by
$p_0+\ldots +p_s$
. The total weight of the edges covered by
![]() ${\mathcal{F}}_j$
is at most
${\mathcal{F}}_j$
is at most
![]() $tp_j$
. Thus, the total weight of the edges in
$tp_j$
. Thus, the total weight of the edges in
![]() $G$
is at most
$G$
is at most
Note that
![]() $p_1\geq \ldots \geq p_s$
implies
$p_1\geq \ldots \geq p_s$
implies
It follows that
By (14) and (15), the total weight of the edges in
![]() $G$
is at most
$G$
is at most
![]() $t(p_{1}+\ldots +p_s)$
.
$t(p_{1}+\ldots +p_s)$
.
Since the probability
the expected value of the total weight of the edges in
![]() $G$
is
$G$
is
![]() $\sum _{j=0}^s tp_j \frac{|{\mathcal{F}}_j|}{\binom {|Y|}{\ell}}$
. Thus (13) follows. In case of equality
$\sum _{j=0}^s tp_j \frac{|{\mathcal{F}}_j|}{\binom {|Y|}{\ell}}$
. Thus (13) follows. In case of equality
![]() $q=0$
. Then for every
$q=0$
. Then for every
![]() $t$
-matching
$t$
-matching
![]() $F_1,F_2,\ldots,F_t$
in
$F_1,F_2,\ldots,F_t$
in
![]() $Y$
,
$Y$
,
![]() ${\mathcal{F}}_0$
has degree 0 and
${\mathcal{F}}_0$
has degree 0 and
![]() ${\mathcal{F}}_i$
has degree
${\mathcal{F}}_i$
has degree
![]() $t$
in
$t$
in
![]() $G$
for
$G$
for
![]() $i=1,\ldots,s$
. Hence the equality holds iff
$i=1,\ldots,s$
. Hence the equality holds iff
![]() ${\mathcal{F}}_{1}= \cdots ={\mathcal{F}}_{s}=\binom{Y}{\ell }$
,
${\mathcal{F}}_{1}= \cdots ={\mathcal{F}}_{s}=\binom{Y}{\ell }$
,
![]() ${\mathcal{F}}_0=\emptyset$
.
${\mathcal{F}}_0=\emptyset$
.
For the proof of Theorem 1.6 we also need the following proposition, which is proved in [Reference Liu and Wang20]. Here we include a short proof for self-containedness.
Proposition 3.3.
For
![]() ${\mathcal{F}} \subset \binom{[n]}{k}$
and
${\mathcal{F}} \subset \binom{[n]}{k}$
and
![]() $1\leq i\lt j\leq n$
,
$1\leq i\lt j\leq n$
,
![]() $|{\mathcal{K}}(S_{ij}({\mathcal{F}}))|\geq |{\mathcal{K}}({\mathcal{F}})|$
.
$|{\mathcal{K}}(S_{ij}({\mathcal{F}}))|\geq |{\mathcal{K}}({\mathcal{F}})|$
.
Proof. We prove the statement by defining an injective map
![]() $\sigma$
from
$\sigma$
from
![]() ${\mathcal{K}}({\mathcal{F}})\setminus{\mathcal{K}}(S_{ij}({\mathcal{F}}))$
to
${\mathcal{K}}({\mathcal{F}})\setminus{\mathcal{K}}(S_{ij}({\mathcal{F}}))$
to
![]() ${\mathcal{K}}(S_{ij}({\mathcal{F}}))\setminus{\mathcal{K}}({\mathcal{F}})$
. Let
${\mathcal{K}}(S_{ij}({\mathcal{F}}))\setminus{\mathcal{K}}({\mathcal{F}})$
. Let
![]() $K\in{\mathcal{K}}({\mathcal{F}})\setminus{\mathcal{K}}(S_{ij}({\mathcal{F}}))$
. Clearly
$K\in{\mathcal{K}}({\mathcal{F}})\setminus{\mathcal{K}}(S_{ij}({\mathcal{F}}))$
. Clearly
![]() $j\in K$
and
$j\in K$
and
![]() $i\notin K$
, and we define
$i\notin K$
, and we define
![]() $\sigma (K)=K'=(K\setminus \{j\})\cup \{i\}$
. We show that
$\sigma (K)=K'=(K\setminus \{j\})\cup \{i\}$
. We show that
![]() $\sigma$
is well-defined by checking
$\sigma$
is well-defined by checking
![]() $K'\in{\mathcal{K}}(S_{ij}({\mathcal{F}}))\setminus{\mathcal{K}}({\mathcal{F}})$
. Firstly, suppose that
$K'\in{\mathcal{K}}(S_{ij}({\mathcal{F}}))\setminus{\mathcal{K}}({\mathcal{F}})$
. Firstly, suppose that
![]() $K'\notin{\mathcal{K}}(S_{ij}({\mathcal{F}}))$
and let
$K'\notin{\mathcal{K}}(S_{ij}({\mathcal{F}}))$
and let
![]() $F'\in \binom{K'}{k}$
be an edge not in
$F'\in \binom{K'}{k}$
be an edge not in
![]() $S_{ij}({\mathcal{F}})$
. If
$S_{ij}({\mathcal{F}})$
. If
![]() $i\notin F'$
then
$i\notin F'$
then
![]() $F'=K\setminus \{j\}$
and
$F'=K\setminus \{j\}$
and
![]() $S_{ij}(F')=F'$
, implying that
$S_{ij}(F')=F'$
, implying that
![]() $F'\in S_{ij}({\mathcal{F}})$
, a contradiction. If
$F'\in S_{ij}({\mathcal{F}})$
, a contradiction. If
![]() $i\in F'$
, then
$i\in F'$
, then
![]() $F=(F'\setminus \{i\})\cup \{j\}\subset K$
is an edge of
$F=(F'\setminus \{i\})\cup \{j\}\subset K$
is an edge of
![]() $\mathcal{F}$
since
$\mathcal{F}$
since
![]() $K\in{\mathcal{K}}({\mathcal{F}})$
. Hence after shifting we have
$K\in{\mathcal{K}}({\mathcal{F}})$
. Hence after shifting we have
![]() $F'\in S_{ij}({\mathcal{F}})$
, a contradiction. This shows
$F'\in S_{ij}({\mathcal{F}})$
, a contradiction. This shows
![]() $K'\in{\mathcal{K}}(S_{ij}({\mathcal{F}}))$
. Secondly, if
$K'\in{\mathcal{K}}(S_{ij}({\mathcal{F}}))$
. Secondly, if
![]() $K'\in{\mathcal{K}}({\mathcal{F}})$
then
$K'\in{\mathcal{K}}({\mathcal{F}})$
then
![]() $K\in{\mathcal{K}}({\mathcal{F}})$
implies
$K\in{\mathcal{K}}({\mathcal{F}})$
implies
![]() $K\in{\mathcal{K}}(S_{ij}({\mathcal{F}}))$
, contradicting the assumption that
$K\in{\mathcal{K}}(S_{ij}({\mathcal{F}}))$
, contradicting the assumption that
![]() $K\notin{\mathcal{K}}(S_{ij}({\mathcal{F}}))$
. Thus
$K\notin{\mathcal{K}}(S_{ij}({\mathcal{F}}))$
. Thus
![]() $K'\in{\mathcal{K}}(S_{ij}({\mathcal{F}}))\setminus{\mathcal{K}}({\mathcal{F}})$
and
$K'\in{\mathcal{K}}(S_{ij}({\mathcal{F}}))\setminus{\mathcal{K}}({\mathcal{F}})$
and
![]() $\sigma$
is indeed a map from
$\sigma$
is indeed a map from
![]() ${\mathcal{K}}({\mathcal{F}})\setminus{\mathcal{K}}(S_{ij}({\mathcal{F}}))$
to
${\mathcal{K}}({\mathcal{F}})\setminus{\mathcal{K}}(S_{ij}({\mathcal{F}}))$
to
![]() ${\mathcal{K}}(S_{ij}({\mathcal{F}}))\setminus{\mathcal{K}}({\mathcal{F}})$
. Clearly,
${\mathcal{K}}(S_{ij}({\mathcal{F}}))\setminus{\mathcal{K}}({\mathcal{F}})$
. Clearly,
![]() $\sigma$
is injective and the proposition follows.
$\sigma$
is injective and the proposition follows.
Proof of Theorem
1.6. Since the shifting operator does not increase the matching number and does not decrease the size of
![]() ${\mathcal{K}}({\mathcal{F}})$
, we may assume that
${\mathcal{K}}({\mathcal{F}})$
, we may assume that
![]() $\mathcal{F}$
is shifted. Let
$\mathcal{F}$
is shifted. Let
![]() ${\mathcal{K}}={\mathcal{K}}({\mathcal{F}})$
and
${\mathcal{K}}={\mathcal{K}}({\mathcal{F}})$
and
![]() ${\mathcal{K}}^*={\mathcal{K}}({\mathcal{E}}(n,k,s))$
. For any
${\mathcal{K}}^*={\mathcal{K}}({\mathcal{E}}(n,k,s))$
. For any
![]() $S\subset [s+1]$
and a family
$S\subset [s+1]$
and a family
![]() ${\mathcal{H}}\subset \binom{[n]}{h}$
, define
${\mathcal{H}}\subset \binom{[n]}{h}$
, define
Clearly
![]() ${\mathcal{H}}(S)\subset \binom{[s+2,n]}{h-|S|}$
.
${\mathcal{H}}(S)\subset \binom{[s+2,n]}{h-|S|}$
.
For
![]() $|S|\geq 3$
, we have
$|S|\geq 3$
, we have
![]() ${\mathcal{K}}^*(S)=\binom{[s+2,n]}{k+1-|S|}$
. It follows that
${\mathcal{K}}^*(S)=\binom{[s+2,n]}{k+1-|S|}$
. It follows that
We are left to compare
![]() $|{\mathcal{K}}(S)|$
with
$|{\mathcal{K}}(S)|$
with
![]() $|{\mathcal{K}}^*(S)|$
for all
$|{\mathcal{K}}^*(S)|$
for all
![]() $S\subset [s+1]$
with
$S\subset [s+1]$
with
![]() $|S|\leq 2$
.
$|S|\leq 2$
.
Claim 2.
![]() ${\mathcal{K}}(\{i\})={\mathcal{F}}(\emptyset )$
for
${\mathcal{K}}(\{i\})={\mathcal{F}}(\emptyset )$
for
![]() $i=1,2,\ldots,s+1$
and
$i=1,2,\ldots,s+1$
and
![]() ${\mathcal{K}}(\{i,j\})={\mathcal{F}}(\{j\})$
for
${\mathcal{K}}(\{i,j\})={\mathcal{F}}(\{j\})$
for
![]() $1\leq i\lt j\leq s+1$
.
$1\leq i\lt j\leq s+1$
.
Proof. For
![]() $F\in{\mathcal{K}}(\{i\})$
,
$F\in{\mathcal{K}}(\{i\})$
,
![]() $F\cup \{i\}\in{\mathcal{K}}$
implies that
$F\cup \{i\}\in{\mathcal{K}}$
implies that
![]() $F\in{\mathcal{F}}(\emptyset )$
. Let
$F\in{\mathcal{F}}(\emptyset )$
. Let
![]() $F\in{\mathcal{F}}(\emptyset )$
. Since
$F\in{\mathcal{F}}(\emptyset )$
. Since
![]() $x\geq s+2\gt i$
each
$x\geq s+2\gt i$
each
![]() $x\in F$
, by shiftedness
$x\in F$
, by shiftedness
![]() $(F\setminus \{x\})\cup \{i\}\in{\mathcal{F}}$
. It follows that
$(F\setminus \{x\})\cup \{i\}\in{\mathcal{F}}$
. It follows that
![]() $\binom{F\cup \{i\}}{k}\subset{\mathcal{F}}$
and
$\binom{F\cup \{i\}}{k}\subset{\mathcal{F}}$
and
![]() $F\cup \{i\}\in{\mathcal{K}}$
. Thus
$F\cup \{i\}\in{\mathcal{K}}$
. Thus
![]() $F\in{\mathcal{K}}(\{i\})$
. Therefore
$F\in{\mathcal{K}}(\{i\})$
. Therefore
![]() ${\mathcal{K}}(\{i\})={\mathcal{F}}(\emptyset )$
.
${\mathcal{K}}(\{i\})={\mathcal{F}}(\emptyset )$
.
For any
![]() $E\in{\mathcal{K}}(\{i,j\})$
we have
$E\in{\mathcal{K}}(\{i,j\})$
we have
![]() $\binom{E\cup \{i,j\}}{k}\subset{\mathcal{F}}$
. It follows that
$\binom{E\cup \{i,j\}}{k}\subset{\mathcal{F}}$
. It follows that
![]() $E\cup \{j\}\in{\mathcal{F}}$
. Thus
$E\cup \{j\}\in{\mathcal{F}}$
. Thus
![]() $E\in{\mathcal{F}}(\{j\})$
. Let
$E\in{\mathcal{F}}(\{j\})$
. Let
![]() $E\in{\mathcal{F}}(\{j\})$
. By shiftedness and
$E\in{\mathcal{F}}(\{j\})$
. By shiftedness and
![]() $i\lt j$
,
$i\lt j$
,
![]() $E\cup \{i\}\in{\mathcal{F}}$
. Moreover,
$E\cup \{i\}\in{\mathcal{F}}$
. Moreover,
![]() $E\cup \{i,j\}\setminus \{x\}\in{\mathcal{F}}$
for each
$E\cup \{i,j\}\setminus \{x\}\in{\mathcal{F}}$
for each
![]() $x\in E$
. That is,
$x\in E$
. That is,
![]() $\binom{E\cup \{i,j\}}{k}\subset{\mathcal{F}}$
and
$\binom{E\cup \{i,j\}}{k}\subset{\mathcal{F}}$
and
![]() $E\cup \{i,j\}\in{\mathcal{K}}$
. Thus
$E\cup \{i,j\}\in{\mathcal{K}}$
. Thus
![]() $E\in{\mathcal{K}}(\{i,j\})$
. Therefore
$E\in{\mathcal{K}}(\{i,j\})$
. Therefore
![]() ${\mathcal{K}}(\{i,j\})={\mathcal{F}}(\{j\})$
.
${\mathcal{K}}(\{i,j\})={\mathcal{F}}(\{j\})$
.
Note that for any
![]() $K\in{\mathcal{K}}(\emptyset )$
we have
$K\in{\mathcal{K}}(\emptyset )$
we have
![]() $\binom{K}{k}\subset{\mathcal{F}}(\emptyset )$
. It follows that
$\binom{K}{k}\subset{\mathcal{F}}(\emptyset )$
. It follows that
![]() $\partial{\mathcal{K}}(\emptyset )\subset{\mathcal{F}}(\emptyset )$
. Since
$\partial{\mathcal{K}}(\emptyset )\subset{\mathcal{F}}(\emptyset )$
. Since
![]() $\nu ({\mathcal{K}}(\emptyset )) \leq s$
, by (8) we have
$\nu ({\mathcal{K}}(\emptyset )) \leq s$
, by (8) we have
By Claim 2,
and
It follows that
 \begin{align} \sum _{S\in [n],|S|\leq 2} |{\mathcal{K}}(S)| &=|{\mathcal{K}}(\emptyset )|+\sum _{1\leq i\leq s+1}|{\mathcal{K}}(\{i\})|+\sum _{1\leq i\lt j\leq s+1}|{\mathcal{K}}(\{i,j\})|\nonumber \\ &\overset{(17)}{\leq } s|{\mathcal{F}}(\emptyset )|+(s+1)|{\mathcal{F}}(\emptyset )|+\sum _{2\leq j\leq s+1}(j-1)|{\mathcal{F}}(\{j\})|\nonumber \\ &\leq (2s+1)|{\mathcal{F}}(\emptyset )|+\sum _{2\leq j\leq s+1}(j-1)|{\mathcal{F}}(\{j\})|. \end{align}
\begin{align} \sum _{S\in [n],|S|\leq 2} |{\mathcal{K}}(S)| &=|{\mathcal{K}}(\emptyset )|+\sum _{1\leq i\leq s+1}|{\mathcal{K}}(\{i\})|+\sum _{1\leq i\lt j\leq s+1}|{\mathcal{K}}(\{i,j\})|\nonumber \\ &\overset{(17)}{\leq } s|{\mathcal{F}}(\emptyset )|+(s+1)|{\mathcal{F}}(\emptyset )|+\sum _{2\leq j\leq s+1}(j-1)|{\mathcal{F}}(\{j\})|\nonumber \\ &\leq (2s+1)|{\mathcal{F}}(\emptyset )|+\sum _{2\leq j\leq s+1}(j-1)|{\mathcal{F}}(\{j\})|. \end{align}
Again by shiftedness
![]() $\partial{\mathcal{F}}(\emptyset )\subset{\mathcal{F}}(\{s+1\})$
, and using (8) we infer
$\partial{\mathcal{F}}(\emptyset )\subset{\mathcal{F}}(\{s+1\})$
, and using (8) we infer
Substituting (19) into (18), we arrive at
 \begin{align*} \sum _{S\in [n],|S|\leq 2} |{\mathcal{K}}(S)| &\leq \sum _{2\leq j\leq s}(j-1)|{\mathcal{F}}(\{j\})|+ s|{\mathcal{F}}(\{s+1\})|+(2s+1)s|{\mathcal{F}}(\{s+1\})|\\[5pt] &= |{\mathcal{F}}(\{2\})|+\sum _{3\leq j\leq s}(j-1)|{\mathcal{F}}(\{j\})|+2s(s+1)|{\mathcal{F}}(\{s+1\})|\\[5pt] &\leq \frac{1}{2}|{\mathcal{F}}(\{1\})|+\frac{1}{2}|{\mathcal{F}}(\{2\})|+\sum _{3\leq j\leq s}(j-1)|{\mathcal{F}}(\{j\})|+2s(s+1)|{\mathcal{F}}(\{s+1\})|. \end{align*}
\begin{align*} \sum _{S\in [n],|S|\leq 2} |{\mathcal{K}}(S)| &\leq \sum _{2\leq j\leq s}(j-1)|{\mathcal{F}}(\{j\})|+ s|{\mathcal{F}}(\{s+1\})|+(2s+1)s|{\mathcal{F}}(\{s+1\})|\\[5pt] &= |{\mathcal{F}}(\{2\})|+\sum _{3\leq j\leq s}(j-1)|{\mathcal{F}}(\{j\})|+2s(s+1)|{\mathcal{F}}(\{s+1\})|\\[5pt] &\leq \frac{1}{2}|{\mathcal{F}}(\{1\})|+\frac{1}{2}|{\mathcal{F}}(\{2\})|+\sum _{3\leq j\leq s}(j-1)|{\mathcal{F}}(\{j\})|+2s(s+1)|{\mathcal{F}}(\{s+1\})|. \end{align*}
By shiftedness,
![]() ${\mathcal{F}}(\{1\})\supset \cdots \supset{\mathcal{F}}(\{s+1\})$
are overlapping families. Set
${\mathcal{F}}(\{1\})\supset \cdots \supset{\mathcal{F}}(\{s+1\})$
are overlapping families. Set
and set
Then
![]() $p_0\geq p_1\geq \ldots \geq p_s$
and by
$p_0\geq p_1\geq \ldots \geq p_s$
and by
![]() $s\geq 3$
,
$s\geq 3$
,
By Lemma 3.2, for
![]() $n-s-1\geq (5s+13)(k-1)\geq (d_{\vec{p}}+1)(k-1)$
we have
$n-s-1\geq (5s+13)(k-1)\geq (d_{\vec{p}}+1)(k-1)$
we have
 \begin{align} \sum _{S\subset [s+1],|S|\leq 2} |{\mathcal{K}}(S)|&\leq (p_1+p_2+\ldots +p_s)\binom{n-s-1}{k-1}\nonumber \\[5pt]&= \binom{s}{2}\binom{n-s-1}{k-1}\nonumber \\ &= \sum _{S\subset [s+1],|S|\leq 2} |{\mathcal{K}}^*(S)|. \end{align}
\begin{align} \sum _{S\subset [s+1],|S|\leq 2} |{\mathcal{K}}(S)|&\leq (p_1+p_2+\ldots +p_s)\binom{n-s-1}{k-1}\nonumber \\[5pt]&= \binom{s}{2}\binom{n-s-1}{k-1}\nonumber \\ &= \sum _{S\subset [s+1],|S|\leq 2} |{\mathcal{K}}^*(S)|. \end{align}
Adding (16) and (20), we conclude that
Let
![]() $\mathcal{F}$
be a family with
$\mathcal{F}$
be a family with
![]() $\nu ({\mathcal{F}})\leq s$
and
$\nu ({\mathcal{F}})\leq s$
and
![]() $|{\mathcal{K}}({\mathcal{F}})|= |{\mathcal{K}}({\mathcal{E}}(n,k,s))|$
. If
$|{\mathcal{K}}({\mathcal{F}})|= |{\mathcal{K}}({\mathcal{E}}(n,k,s))|$
. If
![]() $\mathcal{F}$
is shifted, then by Lemma 3.2 we have
$\mathcal{F}$
is shifted, then by Lemma 3.2 we have
![]() ${\mathcal{F}}(\{s+1\})=\emptyset$
. It follows that
${\mathcal{F}}(\{s+1\})=\emptyset$
. It follows that
![]() ${\mathcal{F}}={\mathcal{E}}(n,k,s)$
. Now assume that
${\mathcal{F}}={\mathcal{E}}(n,k,s)$
. Now assume that
![]() $\mathcal{F}$
is not shifted. Then it changes to
$\mathcal{F}$
is not shifted. Then it changes to
![]() ${\mathcal{E}}(n,k,s)$
by applying shifting repeatedly. Let
${\mathcal{E}}(n,k,s)$
by applying shifting repeatedly. Let
![]() $\mathcal{G}$
be the last family that is not isomorphic to
$\mathcal{G}$
be the last family that is not isomorphic to
![]() ${\mathcal{E}}(n,k,s)$
in this process. That is,
${\mathcal{E}}(n,k,s)$
in this process. That is,
![]() $\mathcal{G}$
is not isomorphic to
$\mathcal{G}$
is not isomorphic to
![]() ${\mathcal{E}}(n,k,s)$
but
${\mathcal{E}}(n,k,s)$
but
![]() $S_{ij}({\mathcal{G}})$
is isomorphic to
$S_{ij}({\mathcal{G}})$
is isomorphic to
![]() ${\mathcal{E}}(n,k,s)$
for some
${\mathcal{E}}(n,k,s)$
for some
![]() $1\leq i\lt j\leq n$
. By symmetry, we may assume that
$1\leq i\lt j\leq n$
. By symmetry, we may assume that
![]() ${\mathcal{G}}\neq{\mathcal{E}}(n,k,s)$
and
${\mathcal{G}}\neq{\mathcal{E}}(n,k,s)$
and
![]() $S_{s,s+1}({\mathcal{G}})={\mathcal{E}}(n,k,s)$
. Let
$S_{s,s+1}({\mathcal{G}})={\mathcal{E}}(n,k,s)$
. Let
 \begin{align*} &{\mathcal{G}}(s\overline{(s+1)}) =\left \{E\in \binom{[n]\setminus \{s,s+1\}}{k-1}\colon E\cup \{s\}\in{\mathcal{G}} \right \},\\[5pt] &{\mathcal{G}}(\overline{s}(s+1)) =\left \{E\in \binom{[n]\setminus \{s,s+1\}}{k-1}\colon E\cup \{s+1\}\in{\mathcal{G}} \right \}. \end{align*}
\begin{align*} &{\mathcal{G}}(s\overline{(s+1)}) =\left \{E\in \binom{[n]\setminus \{s,s+1\}}{k-1}\colon E\cup \{s\}\in{\mathcal{G}} \right \},\\[5pt] &{\mathcal{G}}(\overline{s}(s+1)) =\left \{E\in \binom{[n]\setminus \{s,s+1\}}{k-1}\colon E\cup \{s+1\}\in{\mathcal{G}} \right \}. \end{align*}
Since
![]() $S_{s,s+1}({\mathcal{G}})={\mathcal{E}}(n,k,s)$
, we see
$S_{s,s+1}({\mathcal{G}})={\mathcal{E}}(n,k,s)$
, we see
![]() ${\mathcal{G}}(s\overline{(s+1)})\cup{\mathcal{G}}(\overline{s}(s+1)) =\binom{[n]\setminus \{s,s+1\}}{k-1}$
and
${\mathcal{G}}(s\overline{(s+1)})\cup{\mathcal{G}}(\overline{s}(s+1)) =\binom{[n]\setminus \{s,s+1\}}{k-1}$
and
![]() ${\mathcal{G}}(s\overline{(s+1)})\cap{\mathcal{G}}(\overline{s}(s+1)) =\emptyset$
. It follows that for each
${\mathcal{G}}(s\overline{(s+1)})\cap{\mathcal{G}}(\overline{s}(s+1)) =\emptyset$
. It follows that for each
![]() $E\in \binom{[n]\setminus \{s,s+1\}}{k-1}$
, exactly one of
$E\in \binom{[n]\setminus \{s,s+1\}}{k-1}$
, exactly one of
![]() $E\cup \{s\}\in{\mathcal{G}}$
and
$E\cup \{s\}\in{\mathcal{G}}$
and
![]() $E\cup \{s+1\}\in{\mathcal{G}}$
holds. Now consider a graph
$E\cup \{s+1\}\in{\mathcal{G}}$
holds. Now consider a graph
![]() $G$
on the vertex set
$G$
on the vertex set
![]() $\binom{[n]\setminus \{s,s+1\}}{k-1}$
where
$\binom{[n]\setminus \{s,s+1\}}{k-1}$
where
![]() $(E_1,E_2)$
forms an edge if and only if
$(E_1,E_2)$
forms an edge if and only if
![]() $|E_1\cap E_2|=k-2$
. It is easy to see that
$|E_1\cap E_2|=k-2$
. It is easy to see that
![]() $G$
is a connected graph. Since
$G$
is a connected graph. Since
![]() $\mathcal{G}$
is not isomorphic to
$\mathcal{G}$
is not isomorphic to
![]() ${\mathcal{E}}(n,k,s)$
, we infer that
${\mathcal{E}}(n,k,s)$
, we infer that
![]() ${\mathcal{G}}(s\overline{(s+1)})\neq \emptyset$
and
${\mathcal{G}}(s\overline{(s+1)})\neq \emptyset$
and
![]() ${\mathcal{G}}(\overline{s}(s+1))\neq \emptyset$
. Then there exists an edge
${\mathcal{G}}(\overline{s}(s+1))\neq \emptyset$
. Then there exists an edge
![]() $(E_1,E_2)$
in
$(E_1,E_2)$
in
![]() $G$
such that
$G$
such that
![]() $E_1\cup \{s\}\in{\mathcal{G}}$
and
$E_1\cup \{s\}\in{\mathcal{G}}$
and
![]() $E_2\cup \{s+1\}\in{\mathcal{G}}$
. Let
$E_2\cup \{s+1\}\in{\mathcal{G}}$
. Let
![]() $F\;:\!=\;E_1\cup E_2\in \binom{[n]\setminus \{s,s+1\}}{k}$
. Then
$F\;:\!=\;E_1\cup E_2\in \binom{[n]\setminus \{s,s+1\}}{k}$
. Then
![]() $F\cup \{s+1\}\notin{\mathcal{K}}({\mathcal{G}})$
and
$F\cup \{s+1\}\notin{\mathcal{K}}({\mathcal{G}})$
and
![]() $F\cup \{s\}\notin{\mathcal{K}}({\mathcal{G}})$
. But
$F\cup \{s\}\notin{\mathcal{K}}({\mathcal{G}})$
. But
![]() $S_{s,s+1}({\mathcal{G}})={\mathcal{E}}(n,k,s)$
implies
$S_{s,s+1}({\mathcal{G}})={\mathcal{E}}(n,k,s)$
implies
![]() $F\cup \{s\} \in{\mathcal{K}}(S_{s,s+1}({\mathcal{G}}))$
. Moreover, for any
$F\cup \{s\} \in{\mathcal{K}}(S_{s,s+1}({\mathcal{G}}))$
. Moreover, for any
![]() $K\in{\mathcal{K}}({\mathcal{G}})\setminus{\mathcal{K}}(S_{s,s+1}({\mathcal{G}}))$
, we have
$K\in{\mathcal{K}}({\mathcal{G}})\setminus{\mathcal{K}}(S_{s,s+1}({\mathcal{G}}))$
, we have
![]() $(K\setminus \{s+1\})\cup \{s\}\in{\mathcal{K}}(S_{s,s+1}({\mathcal{G}}))\setminus{\mathcal{K}}({\mathcal{G}})$
by the injective map defined in Proposition 3.3. Hence
$(K\setminus \{s+1\})\cup \{s\}\in{\mathcal{K}}(S_{s,s+1}({\mathcal{G}}))\setminus{\mathcal{K}}({\mathcal{G}})$
by the injective map defined in Proposition 3.3. Hence
![]() $|{\mathcal{K}}(S_{s,s+1}({\mathcal{G}}))|\gt |{\mathcal{K}}({\mathcal{G}})|\geq |{\mathcal{K}}({\mathcal{F}})|=|{\mathcal{K}}({\mathcal{E}}(n,k,s))|$
, a contradiction. Thus up to isomorphism
$|{\mathcal{K}}(S_{s,s+1}({\mathcal{G}}))|\gt |{\mathcal{K}}({\mathcal{G}})|\geq |{\mathcal{K}}({\mathcal{F}})|=|{\mathcal{K}}({\mathcal{E}}(n,k,s))|$
, a contradiction. Thus up to isomorphism
![]() ${\mathcal{E}}(n,k,s)$
is the only family attaining equality.
${\mathcal{E}}(n,k,s)$
is the only family attaining equality.
4. The maximum size of an
 $r$
-complete intersecting family
$r$
-complete intersecting family
In this section, we determine
![]() $f(n,k,r)$
for all
$f(n,k,r)$
for all
![]() $k,r\geq 3$
and
$k,r\geq 3$
and
![]() $n\geq n_0(k,r)$
, thereby proving Theorem 1.5.
$n\geq n_0(k,r)$
, thereby proving Theorem 1.5.
Proposition 4.1.
For
![]() $r\geq k+1$
,
$r\geq k+1$
,
![]() $f(n,k,r)=0$
. For
$f(n,k,r)=0$
. For
![]() $n\geq 2k-1$
,
$n\geq 2k-1$
,
Moreover, the unique family satisfying the condition is
![]() $\binom{X}{k}$
with
$\binom{X}{k}$
with
![]() $|X|=2k-1$
.
$|X|=2k-1$
.
Proof. Suppose that
![]() $\mathcal{F}$
is an intersecting
$\mathcal{F}$
is an intersecting
![]() $k$
-graph and each
$k$
-graph and each
![]() $F\in{\mathcal{F}}$
is
$F\in{\mathcal{F}}$
is
![]() $k$
-wise covered. Consider the bipartite graph with partite sets
$k$
-wise covered. Consider the bipartite graph with partite sets
![]() $\mathcal{F}$
,
$\mathcal{F}$
,
![]() $\partial{\mathcal{F}}$
and an edge between
$\partial{\mathcal{F}}$
and an edge between
![]() $F$
and
$F$
and
![]() $G$
iff
$G$
iff
![]() $G\subset F$
. It is clear that each
$G\subset F$
. It is clear that each
![]() $F\in{\mathcal{F}}$
has degree
$F\in{\mathcal{F}}$
has degree
![]() $k$
. On the other hand, the condition implies that each
$k$
. On the other hand, the condition implies that each
![]() $G\in \partial{\mathcal{F}}$
has degree at least
$G\in \partial{\mathcal{F}}$
has degree at least
![]() $k$
. Consequently,
$k$
. Consequently,
![]() $|{\mathcal{F}}|\geq |\partial{\mathcal{F}}|$
. In view of (7), we see
$|{\mathcal{F}}|\geq |\partial{\mathcal{F}}|$
. In view of (7), we see
![]() $|{\mathcal{F}}|= |\partial{\mathcal{F}}|$
and equality holds iff
$|{\mathcal{F}}|= |\partial{\mathcal{F}}|$
and equality holds iff
![]() ${\mathcal{F}}=\binom{X}{k}$
with
${\mathcal{F}}=\binom{X}{k}$
with
![]() $|X|=2k-1$
. The same argument implies
$|X|=2k-1$
. The same argument implies
![]() $f(n,k,r)=0$
for
$f(n,k,r)=0$
for
![]() $r\geq k+1$
.
$r\geq k+1$
.
We need a notion of basis for an intersecting family inspired by [Reference Frankl6]. For any intersecting family
![]() ${\mathcal{F}}\subset \binom{[n]}{k}$
, we define a basis
${\mathcal{F}}\subset \binom{[n]}{k}$
, we define a basis
![]() ${\mathcal{B}}({\mathcal{F}})$
which is not necessarily unique by the following process. We start with
${\mathcal{B}}({\mathcal{F}})$
which is not necessarily unique by the following process. We start with
![]() ${\mathcal{F}}^0={\mathcal{F}}$
. Note that
${\mathcal{F}}^0={\mathcal{F}}$
. Note that
![]() ${\mathcal{F}}^0$
is an antichain. A collection of sets
${\mathcal{F}}^0$
is an antichain. A collection of sets
![]() $F_0,\ldots,F_k$
is called a sunflower of size
$F_0,\ldots,F_k$
is called a sunflower of size
![]() $k+1$
with centre
$k+1$
with centre
![]() $C$
if
$C$
if
![]() $F_i\cap F_j=C$
for all distinct
$F_i\cap F_j=C$
for all distinct
![]() $i,j\in \{0,1,\ldots,k\}$
. Note that in this case
$i,j\in \{0,1,\ldots,k\}$
. Note that in this case
![]() $F_0\setminus C,\ldots,F_k\setminus C$
are pairwise disjoint. At the
$F_0\setminus C,\ldots,F_k\setminus C$
are pairwise disjoint. At the
![]() $i$
-th step try and find in the current family
$i$
-th step try and find in the current family
![]() ${\mathcal{F}}^i$
a sunflower
${\mathcal{F}}^i$
a sunflower
![]() $F_0,\ldots,F_k$
of size
$F_0,\ldots,F_k$
of size
![]() $k+1$
(the size of
$k+1$
(the size of
![]() $F_j$
may be distinct). Let
$F_j$
may be distinct). Let
![]() $C_i$
be the centre of the sunflower. Then let
$C_i$
be the centre of the sunflower. Then let
![]() ${\mathcal{F}}^{i+1}$
be the family obtained from
${\mathcal{F}}^{i+1}$
be the family obtained from
![]() ${\mathcal{F}}^i$
by deleting all sets containing
${\mathcal{F}}^i$
by deleting all sets containing
![]() $C_i$
and adding
$C_i$
and adding
![]() $C_i$
. Clearly
$C_i$
. Clearly
![]() ${\mathcal{F}}^{i+1}$
is also an antichain.
${\mathcal{F}}^{i+1}$
is also an antichain.
Claim 3.
If
![]() ${\mathcal{F}}^i$
is intersecting, then
${\mathcal{F}}^i$
is intersecting, then
![]() ${\mathcal{F}}^{i+1}$
is also intersecting.
${\mathcal{F}}^{i+1}$
is also intersecting.
Proof. Take an arbitrary set
![]() $F$
from
$F$
from
![]() ${\mathcal{F}}^{i}$
. Since
${\mathcal{F}}^{i}$
. Since
![]() $|F|\leq k$
, we have
$|F|\leq k$
, we have
![]() $F\cap (F_j\setminus C_i)=\emptyset$
for some
$F\cap (F_j\setminus C_i)=\emptyset$
for some
![]() $j$
,
$j$
,
![]() $0\leq j\leq k$
. Then
$0\leq j\leq k$
. Then
![]() $F\cap C_i=F\cap F_j\neq \emptyset$
.
$F\cap C_i=F\cap F_j\neq \emptyset$
.
Continue this process until no more sunflowers of size
![]() $k+1$
can be formed. Let
$k+1$
can be formed. Let
![]() ${\mathcal{B}}({\mathcal{F}})$
be the final family. Clearly,
${\mathcal{B}}({\mathcal{F}})$
be the final family. Clearly,
![]() ${\mathcal{B}}({\mathcal{F}})$
is an antichain and for all
${\mathcal{B}}({\mathcal{F}})$
is an antichain and for all
![]() $F\in{\mathcal{F}}$
there exists
$F\in{\mathcal{F}}$
there exists
![]() $B\in{\mathcal{B}}({\mathcal{F}})$
with
$B\in{\mathcal{B}}({\mathcal{F}})$
with
![]() $B\subset F$
. By Claim 3,
$B\subset F$
. By Claim 3,
![]() ${\mathcal{B}}({\mathcal{F}})$
is intersecting. In view of the Erdős-Rado sunflower lemma [Reference Erdős and Rado4],
${\mathcal{B}}({\mathcal{F}})$
is intersecting. In view of the Erdős-Rado sunflower lemma [Reference Erdős and Rado4],
Proof of Theorem
1.5. By proposition 4.1, we may assume
![]() $3\leq r\leq k$
. Let
$3\leq r\leq k$
. Let
![]() $\mathcal{F}$
be an
$\mathcal{F}$
be an
![]() $r$
-complete intersecting family of maximal size and let
$r$
-complete intersecting family of maximal size and let
![]() ${\mathcal{B}}={\mathcal{B}}({\mathcal{F}})$
be its basis. Let
${\mathcal{B}}={\mathcal{B}}({\mathcal{F}})$
be its basis. Let
![]() $X=\mathop{\cup }\limits _{B\in{\mathcal{B}}} B$
. By (21) we have
$X=\mathop{\cup }\limits _{B\in{\mathcal{B}}} B$
. By (21) we have
By the definition of
![]() $\mathcal{B}$
, for any
$\mathcal{B}$
, for any
![]() $F\in{\mathcal{F}}$
there exists
$F\in{\mathcal{F}}$
there exists
![]() $B\in{\mathcal{B}}$
such that
$B\in{\mathcal{B}}$
such that
![]() $B\subset F$
. Then for
$B\subset F$
. Then for
![]() $F,F'\in{\mathcal{F}}$
, there exist
$F,F'\in{\mathcal{F}}$
, there exist
![]() $B,B'\in{\mathcal{B}}$
such that
$B,B'\in{\mathcal{B}}$
such that
![]() $B\subset F$
and
$B\subset F$
and
![]() $B'\subset F'$
. Since
$B'\subset F'$
. Since
![]() $\mathcal{B}$
is intersecting,
$\mathcal{B}$
is intersecting,
![]() $\emptyset \neq B\cap B'\subset F\cap F'\cap X$
. Thus, for all
$\emptyset \neq B\cap B'\subset F\cap F'\cap X$
. Thus, for all
![]() $F,F'\in{\mathcal{F}}$
,
$F,F'\in{\mathcal{F}}$
,
![]() $F\cap F'\cap X \neq \emptyset$
.
$F\cap F'\cap X \neq \emptyset$
.
Let us define
![]() $p=\min \left \{|F\cap X|\colon F\in{\mathcal{F}}\right \}$
and choose an arbitrary pair
$p=\min \left \{|F\cap X|\colon F\in{\mathcal{F}}\right \}$
and choose an arbitrary pair
![]() $(F,P_0)$
,
$(F,P_0)$
,
![]() $P_0\in \binom{X}{p}$
,
$P_0\in \binom{X}{p}$
,
![]() $F\cap X=P_0$
. Set
$F\cap X=P_0$
. Set
![]() $H=F\setminus P_0$
and define
$H=F\setminus P_0$
and define
Note that
![]() $P_0\in{\mathcal{P}}(H)$
.
$P_0\in{\mathcal{P}}(H)$
.
Claim 4.
![]() ${\mathcal{P}}(H)$
is intersecting and
${\mathcal{P}}(H)$
is intersecting and
![]() $r$
-complete.
$r$
-complete.
Proof. For
![]() $P,P'\in{\mathcal{P}}(H)$
fix
$P,P'\in{\mathcal{P}}(H)$
fix
![]() $B,B'\in{\mathcal{B}}({\mathcal{F}})$
satisfying
$B,B'\in{\mathcal{B}}({\mathcal{F}})$
satisfying
![]() $B\subset H\cup P, B'\subset H\cup P'$
. Since
$B\subset H\cup P, B'\subset H\cup P'$
. Since
![]() $H\cap X=\emptyset$
,
$H\cap X=\emptyset$
,
![]() $B\subset P$
and
$B\subset P$
and
![]() $B'\subset P'$
. Consequently,
$B'\subset P'$
. Consequently,
![]() $P\cap P'\supset B\cap B'\neq \emptyset$
.
$P\cap P'\supset B\cap B'\neq \emptyset$
.
Let us prove the
![]() $r$
-completeness of
$r$
-completeness of
![]() ${\mathcal{P}}(H)$
next. Fix
${\mathcal{P}}(H)$
next. Fix
![]() $P\in{\mathcal{P}}(H)$
and
$P\in{\mathcal{P}}(H)$
and
![]() $R\in \binom{P}{p-1}$
. Using the
$R\in \binom{P}{p-1}$
. Using the
![]() $r$
-completeness of
$r$
-completeness of
![]() $\mathcal{F}$
there are
$\mathcal{F}$
there are
![]() $r$
distinct elements
$r$
distinct elements
![]() $x_1,x_2,\ldots,x_r$
such that
$x_1,x_2,\ldots,x_r$
such that
![]() $(H\cup R\cup \{x_i\})\in{\mathcal{F}}$
. The minimal choice of
$(H\cup R\cup \{x_i\})\in{\mathcal{F}}$
. The minimal choice of
![]() $p$
implies
$p$
implies
![]() $|(H\cup R\cup \{x_i\})\cap X|\geq p$
, whence
$|(H\cup R\cup \{x_i\})\cap X|\geq p$
, whence
![]() $x_i\in X$
,
$x_i\in X$
,
![]() $1\leq i\leq r$
. Thus
$1\leq i\leq r$
. Thus
![]() $R\cup \{x_i\}\in{\mathcal{P}}(H)$
, proving the
$R\cup \{x_i\}\in{\mathcal{P}}(H)$
, proving the
![]() $r$
-completeness of
$r$
-completeness of
![]() ${\mathcal{P}}(H)$
.
${\mathcal{P}}(H)$
.
If
![]() $p\lt r$
, by Claim 4 and Proposition 4.1 we have
$p\lt r$
, by Claim 4 and Proposition 4.1 we have
![]() $1\leq |{\mathcal{P}}(H)|\leq f(|X|,p,r)=0$
, a contradiction. Thus
$1\leq |{\mathcal{P}}(H)|\leq f(|X|,p,r)=0$
, a contradiction. Thus
![]() $p\geq r$
. Define
$p\geq r$
. Define
Then
 \begin{equation*} |{\mathcal {F}}_0| \leq \sum _{r+1\leq i\leq k} \binom {|X|}{i}\binom {n-|X|}{k-i}\leq \sum _{r+1\leq i\leq k} \binom {k^{2k}}{i}\binom {n-k^{2k}}{k-i} \lt 2\binom {k^{2k}}{r+1}\binom {n-2r}{k-r-1}. \end{equation*}
\begin{equation*} |{\mathcal {F}}_0| \leq \sum _{r+1\leq i\leq k} \binom {|X|}{i}\binom {n-|X|}{k-i}\leq \sum _{r+1\leq i\leq k} \binom {k^{2k}}{i}\binom {n-k^{2k}}{k-i} \lt 2\binom {k^{2k}}{r+1}\binom {n-2r}{k-r-1}. \end{equation*}
If
![]() $p\geq r+1$
, then
$p\geq r+1$
, then
Thus we assume
![]() $p=r$
.
$p=r$
.
If
![]() $|{\mathcal{P}}(H)|\leq \binom{2r-1}{r}-1$
holds for all
$|{\mathcal{P}}(H)|\leq \binom{2r-1}{r}-1$
holds for all
![]() $H\in \binom{[n]\setminus X}{k-r}$
, then
$H\in \binom{[n]\setminus X}{k-r}$
, then
 \begin{align*} |{\mathcal{F}}|&\leq \sum _{H\in \binom{[n]\setminus X}{k-r}}|{\mathcal{P}}(H)|+|{\mathcal{F}}_0|\\[5pt] &\leq \left (\binom{2r-1}{r}-1\right )\binom{n-|X|}{k-r}+2\binom{k^{2k}}{r+1}\binom{n-2r}{k-r-1}\\[5pt] &\leq \binom{2r-1}{r}\binom{n-2r+1}{k-r}\ (\mbox{for } n\geq n_0(k,r))\\[5pt] &\lt |{\mathcal{L}}(n,k,r)|. \end{align*}
\begin{align*} |{\mathcal{F}}|&\leq \sum _{H\in \binom{[n]\setminus X}{k-r}}|{\mathcal{P}}(H)|+|{\mathcal{F}}_0|\\[5pt] &\leq \left (\binom{2r-1}{r}-1\right )\binom{n-|X|}{k-r}+2\binom{k^{2k}}{r+1}\binom{n-2r}{k-r-1}\\[5pt] &\leq \binom{2r-1}{r}\binom{n-2r+1}{k-r}\ (\mbox{for } n\geq n_0(k,r))\\[5pt] &\lt |{\mathcal{L}}(n,k,r)|. \end{align*}
Assume now that for some
![]() $H\in \binom{[n]\setminus X}{k-r}$
,
$H\in \binom{[n]\setminus X}{k-r}$
,
![]() $|{\mathcal{P}}(H)|=\binom{2r-1}{r}$
. By Proposition 4.1 we may assume that
$|{\mathcal{P}}(H)|=\binom{2r-1}{r}$
. By Proposition 4.1 we may assume that
![]() ${\mathcal{P}}(H)=\binom{Y}{r}$
,
${\mathcal{P}}(H)=\binom{Y}{r}$
,
![]() $Y\in \binom{X}{2r-1}$
. We claim that
$Y\in \binom{X}{2r-1}$
. We claim that
![]() $|F\cap Y|\geq r$
for all
$|F\cap Y|\geq r$
for all
![]() $F\in{\mathcal{F}}$
. Indeed the opposite would mean that
$F\in{\mathcal{F}}$
. Indeed the opposite would mean that
![]() $F\cap P=\emptyset$
for some
$F\cap P=\emptyset$
for some
![]() $P\in \binom{Y}{r}$
. Then
$P\in \binom{Y}{r}$
. Then
![]() $F\cap (H\cup P)\cap X=F\cap P=\emptyset$
, a contradiction. Consequently
$F\cap (H\cup P)\cap X=F\cap P=\emptyset$
, a contradiction. Consequently
![]() ${\mathcal{F}}\subset \{F\in \binom{[n]}{k}\colon |F\cap Y|\geq r\}$
, i.e.,
${\mathcal{F}}\subset \{F\in \binom{[n]}{k}\colon |F\cap Y|\geq r\}$
, i.e.,
![]() $\mathcal{F}$
is contained in an isomorphic copy of
$\mathcal{F}$
is contained in an isomorphic copy of
![]() ${\mathcal{L}}(n,k,r)$
.
${\mathcal{L}}(n,k,r)$
.
5. Maximizing the number of
 $r$
-complete sets in an intersecting family
$r$
-complete sets in an intersecting family
In this section, we prove Theorem 1.8 for
![]() $3\leq r\lt k$
and
$3\leq r\lt k$
and
![]() $n\geq n_0(k,r)$
. We need a different notion of basis. For a saturated intersecting family
$n\geq n_0(k,r)$
. We need a different notion of basis. For a saturated intersecting family
![]() $\mathcal{F}$
, define
$\mathcal{F}$
, define
![]() ${\mathcal{B}}({\mathcal{F}})$
be the family of minimal (for containment) sets in
${\mathcal{B}}({\mathcal{F}})$
be the family of minimal (for containment) sets in
![]() ${\mathcal{T}}({\mathcal{F}})$
. Define
${\mathcal{T}}({\mathcal{F}})$
. Define
![]() $X=\mathop{\cup }\limits _{B\in{\mathcal{B}}} B$
the support of
$X=\mathop{\cup }\limits _{B\in{\mathcal{B}}} B$
the support of
![]() $\mathcal{B}$
. The following properties of
$\mathcal{B}$
. The following properties of
![]() ${\mathcal{B}}({\mathcal{F}})$
were proved in [Reference Frankl, Kupavskii and Kiselev10].
${\mathcal{B}}({\mathcal{F}})$
were proved in [Reference Frankl, Kupavskii and Kiselev10].
Lemma 5.1 ([Reference Frankl, Kupavskii and Kiselev10]). Suppose that
![]() ${\mathcal{F}}\subset \binom{[n]}{k}$
is a saturated intersecting family and
${\mathcal{F}}\subset \binom{[n]}{k}$
is a saturated intersecting family and
![]() ${\mathcal{B}}={\mathcal{B}}({\mathcal{F}})$
. Then
${\mathcal{B}}={\mathcal{B}}({\mathcal{F}})$
. Then
-
(i)
 $\mathcal{B}$
is an intersecting antichain,
$\mathcal{B}$
is an intersecting antichain,
-
(ii)
 ${\mathcal{F}}=\{H\in \binom{[n]}{k}\colon \exists B\in{\mathcal{B}}, B\subset H\}$
,
${\mathcal{F}}=\{H\in \binom{[n]}{k}\colon \exists B\in{\mathcal{B}}, B\subset H\}$
, -
(iii) for all
 $F,F'\in{\mathcal{F}}$
,(22)
$F,F'\in{\mathcal{F}}$
,(22) \begin{align} F\cap F'\cap X\neq \emptyset . \end{align}
\begin{align} F\cap F'\cap X\neq \emptyset . \end{align}
The following lemma is essentially proved in [Reference Frankl, Kupavskii and Kiselev10]. For self-containedness we include its proof as well.
Lemma 5.2 ([Reference Frankl, Kupavskii and Kiselev10]). Suppose that
![]() ${\mathcal{F}}\subset \binom{[n]}{k}$
is a saturated intersecting family. Then
${\mathcal{F}}\subset \binom{[n]}{k}$
is a saturated intersecting family. Then
![]() $|{\mathcal{B}}({\mathcal{F}})|\leq k^k$
.
$|{\mathcal{B}}({\mathcal{F}})|\leq k^k$
.
Proof. Let
![]() ${\mathcal{B}}={\mathcal{B}}({\mathcal{F}})$
. For the proof we use a branching process. During the proof a sequence
${\mathcal{B}}={\mathcal{B}}({\mathcal{F}})$
. For the proof we use a branching process. During the proof a sequence
![]() $S=(x_1,x_2,\ldots,x_\ell )$
is an ordered sequence of distinct elements of
$S=(x_1,x_2,\ldots,x_\ell )$
is an ordered sequence of distinct elements of
![]() $[n]$
and we use
$[n]$
and we use
![]() $\widehat{S}$
to denote the underlying unordered set
$\widehat{S}$
to denote the underlying unordered set
![]() $\{x_1,x_2,\ldots,x_\ell \}$
. At the beginning, we assign weight 1 to the empty sequence
$\{x_1,x_2,\ldots,x_\ell \}$
. At the beginning, we assign weight 1 to the empty sequence
![]() $S_{\emptyset }$
. At the first stage, we choose
$S_{\emptyset }$
. At the first stage, we choose
![]() $B_1\in{\mathcal{B}}$
with
$B_1\in{\mathcal{B}}$
with
![]() $|B_1|$
minimal. For any vertex
$|B_1|$
minimal. For any vertex
![]() $x\in B_1$
, define one sequence
$x\in B_1$
, define one sequence
![]() $(x)$
and assign the weight
$(x)$
and assign the weight
![]() $|B_1|^{-1}$
to it.
$|B_1|^{-1}$
to it.
In each subsequent stage, we pick a sequence
![]() $S=(x_1,\ldots,x_p)$
and denote its weight by
$S=(x_1,\ldots,x_p)$
and denote its weight by
![]() $w(S)$
. If
$w(S)$
. If
![]() $\widehat{S}\cap B\neq \emptyset$
holds for all
$\widehat{S}\cap B\neq \emptyset$
holds for all
![]() $B\in{\mathcal{B}}$
then we do nothing. Otherwise we pick
$B\in{\mathcal{B}}$
then we do nothing. Otherwise we pick
![]() $B\in{\mathcal{B}}$
satisfying
$B\in{\mathcal{B}}$
satisfying
![]() $\widehat{S}\cap B= \emptyset$
and replace
$\widehat{S}\cap B= \emptyset$
and replace
![]() $S$
by the
$S$
by the
![]() $|B|$
sequences
$|B|$
sequences
![]() $(x_1,\ldots,x_p,y)$
with
$(x_1,\ldots,x_p,y)$
with
![]() $y\in B$
and assign weight
$y\in B$
and assign weight
![]() $\frac{w(S)}{|B|}$
to each of them. Clearly, the total weight is always 1.
$\frac{w(S)}{|B|}$
to each of them. Clearly, the total weight is always 1.
We continue until
![]() $\widehat{S}\cap B\neq \emptyset$
for all sequences
$\widehat{S}\cap B\neq \emptyset$
for all sequences
![]() $S$
and all
$S$
and all
![]() $B\in{\mathcal{B}}$
. Since
$B\in{\mathcal{B}}$
. Since
![]() $[n]$
is finite, each sequence has length at most
$[n]$
is finite, each sequence has length at most
![]() $n$
and eventually the process stops. Let
$n$
and eventually the process stops. Let
![]() $\mathcal{S}$
be the collection of sequences that survived in the end of the branching process and let
$\mathcal{S}$
be the collection of sequences that survived in the end of the branching process and let
![]() ${\mathcal{S}}^{(\ell )}$
be the collection of sequences in
${\mathcal{S}}^{(\ell )}$
be the collection of sequences in
![]() $\mathcal{S}$
with length
$\mathcal{S}$
with length
![]() $\ell$
.
$\ell$
.
Claim 5.
For each
![]() $B\in{\mathcal{B}}^{(\ell )}$
, there is some sequence
$B\in{\mathcal{B}}^{(\ell )}$
, there is some sequence
![]() $S\in{\mathcal{S}}^{(\ell )}$
with
$S\in{\mathcal{S}}^{(\ell )}$
with
![]() $\widehat{S}=B$
.
$\widehat{S}=B$
.
Proof. Let us suppose the contrary and let
![]() $S=(x_1,\ldots,x_p)$
be a sequence of maximal length that occurred at some stage of the branching process satisfying
$S=(x_1,\ldots,x_p)$
be a sequence of maximal length that occurred at some stage of the branching process satisfying
![]() $\widehat{S}\subsetneqq B$
. Since
$\widehat{S}\subsetneqq B$
. Since
![]() $\mathcal{B}$
are intersecting,
$\mathcal{B}$
are intersecting,
![]() $B_{1}\cap B\neq \emptyset$
, implying that
$B_{1}\cap B\neq \emptyset$
, implying that
![]() $p\geq 1$
. Since
$p\geq 1$
. Since
![]() $\widehat{S}$
is a proper subset of
$\widehat{S}$
is a proper subset of
![]() $B$
and
$B$
and
![]() $B\in{\mathcal{B}}$
, it follows that
$B\in{\mathcal{B}}$
, it follows that
![]() $\widehat{S}\notin{\mathcal{T}}({\mathcal{F}})$
. Thereby there exists
$\widehat{S}\notin{\mathcal{T}}({\mathcal{F}})$
. Thereby there exists
![]() $F\in{\mathcal{F}}$
with
$F\in{\mathcal{F}}$
with
![]() $\widehat{S} \cap F= \emptyset$
. In view of Lemma 5.1 (ii), we can find
$\widehat{S} \cap F= \emptyset$
. In view of Lemma 5.1 (ii), we can find
![]() $B'\in{\mathcal{B}}$
such that
$B'\in{\mathcal{B}}$
such that
![]() $\widehat{S} \cap B'= \emptyset$
. Thus at some point we picked
$\widehat{S} \cap B'= \emptyset$
. Thus at some point we picked
![]() $S$
and some
$S$
and some
![]() $\tilde{B}\in{\mathcal{B}}$
with
$\tilde{B}\in{\mathcal{B}}$
with
![]() $\widehat{S} \cap \tilde{B}= \emptyset$
. Since
$\widehat{S} \cap \tilde{B}= \emptyset$
. Since
![]() $\mathcal{B}$
is intersecting,
$\mathcal{B}$
is intersecting,
![]() $B\cap \tilde{B}\neq \emptyset$
. Consequently, for each
$B\cap \tilde{B}\neq \emptyset$
. Consequently, for each
![]() $y\in B\cap \tilde{B}$
the sequence
$y\in B\cap \tilde{B}$
the sequence
![]() $(x_1,\ldots,x_p,y)$
occurred in the branching process. This contradicts the maximality of
$(x_1,\ldots,x_p,y)$
occurred in the branching process. This contradicts the maximality of
![]() $p$
. Hence there is an
$p$
. Hence there is an
![]() $S$
at some stage satisfying
$S$
at some stage satisfying
![]() $\widehat{S}= B$
. Since
$\widehat{S}= B$
. Since
![]() $\mathcal{B}$
is intersecting,
$\mathcal{B}$
is intersecting,
![]() $\widehat{S}\cap B'=B\cap B'\neq \emptyset$
for all
$\widehat{S}\cap B'=B\cap B'\neq \emptyset$
for all
![]() $B'\in{\mathcal{B}}$
. Thus
$B'\in{\mathcal{B}}$
. Thus
![]() $\widehat{S}\in{\mathcal{S}}$
and the claim holds.
$\widehat{S}\in{\mathcal{S}}$
and the claim holds.
By Claim 5, we see that
![]() $|{\mathcal{B}}^{(\ell )}|\leq |{\mathcal{S}}^{(\ell )}|$
for all
$|{\mathcal{B}}^{(\ell )}|\leq |{\mathcal{S}}^{(\ell )}|$
for all
![]() $\ell \geq 1$
. Let
$\ell \geq 1$
. Let
![]() $S=(x_1,\ldots,x_\ell )\in{\mathcal{S}}^{(\ell )}$
and let
$S=(x_1,\ldots,x_\ell )\in{\mathcal{S}}^{(\ell )}$
and let
![]() $S_i=(x_1,\ldots,x_i)$
for
$S_i=(x_1,\ldots,x_i)$
for
![]() $i=1,\ldots,\ell$
. At the first stage,
$i=1,\ldots,\ell$
. At the first stage,
![]() $w(S_1)=1/|B_1|$
. Assume that
$w(S_1)=1/|B_1|$
. Assume that
![]() $B_{i}$
is the selected set when replacing
$B_{i}$
is the selected set when replacing
![]() $S_{i-1}$
in the branching process for
$S_{i-1}$
in the branching process for
![]() $i=2,\ldots,\ell$
. Then
$i=2,\ldots,\ell$
. Then
 \begin{equation*} w(S)= \prod _{i=1}^\ell \frac {1}{|B_{i}|} \geq k^{-\ell }. \end{equation*}
\begin{equation*} w(S)= \prod _{i=1}^\ell \frac {1}{|B_{i}|} \geq k^{-\ell }. \end{equation*}
It follows that
Thus
![]() $|{\mathcal{B}}|=\sum \limits _{1\leq \ell \leq k}|{\mathcal{B}}^{(\ell )}| \leq k^k$
.
$|{\mathcal{B}}|=\sum \limits _{1\leq \ell \leq k}|{\mathcal{B}}^{(\ell )}| \leq k^k$
.
Proposition 5.3.
If
![]() $\partial{\mathcal{F}}$
is intersecting, then
$\partial{\mathcal{F}}$
is intersecting, then
![]() $\mathcal{F}$
is 3-intersecting.
$\mathcal{F}$
is 3-intersecting.
Proof. Suppose that
![]() $|F\cap F'|\leq 2$
and
$|F\cap F'|\leq 2$
and
![]() $F,F'\in{\mathcal{F}}$
. If
$F,F'\in{\mathcal{F}}$
. If
![]() $F\cap F'=\{x,x'\}$
then
$F\cap F'=\{x,x'\}$
then
![]() $F\setminus \{x\}, F'\setminus \{x'\}\in \partial{\mathcal{F}}$
and they are disjoint, a contradiction. The case
$F\setminus \{x\}, F'\setminus \{x'\}\in \partial{\mathcal{F}}$
and they are disjoint, a contradiction. The case
![]() $F\cap F'=\{x\}$
is even easier.
$F\cap F'=\{x\}$
is even easier.
Proposition 5.4.
Let
![]() ${\mathcal{F}}\subset \binom{[n]}{3}$
be a saturated intersecting family and let
${\mathcal{F}}\subset \binom{[n]}{3}$
be a saturated intersecting family and let
![]() ${\mathcal{F}}^*$
be the family of
${\mathcal{F}}^*$
be the family of
![]() $r$
-complete sets in
$r$
-complete sets in
![]() $\mathcal{F}$
. For
$\mathcal{F}$
. For
![]() $r=3$
,
$r=3$
,
![]() $|{\mathcal{F}}^*|\leq \binom{5}{3}$
with equality holding iff
$|{\mathcal{F}}^*|\leq \binom{5}{3}$
with equality holding iff
![]() ${\mathcal{F}}=\binom{[5]}{3}$
up to isomorphism. For
${\mathcal{F}}=\binom{[5]}{3}$
up to isomorphism. For
![]() $r\geq 4$
,
$r\geq 4$
,
![]() $|{\mathcal{F}}^*|\leq 1$
with equality holding iff
$|{\mathcal{F}}^*|\leq 1$
with equality holding iff
![]() ${\mathcal{F}}={\mathcal{L}}(n,3,2)$
up to isomorphism.
${\mathcal{F}}={\mathcal{L}}(n,3,2)$
up to isomorphism.
Proof. Let
![]() $r=3$
. Suppose that there exist two edges intersecting in one vertex, say
$r=3$
. Suppose that there exist two edges intersecting in one vertex, say
![]() $(x_1,x_2,z), (y_1,y_2,z)\in{\mathcal{F}}^*$
, since
$(x_1,x_2,z), (y_1,y_2,z)\in{\mathcal{F}}^*$
, since
![]() $(x_1,x_2)$
is 3-fold covered and
$(x_1,x_2)$
is 3-fold covered and
![]() $\mathcal{F}$
is intersecting, we have
$\mathcal{F}$
is intersecting, we have
![]() $(x_1,x_2,y_i)\in{\mathcal{F}}$
,
$(x_1,x_2,y_i)\in{\mathcal{F}}$
,
![]() $i=1,2$
. Similarly,
$i=1,2$
. Similarly,
![]() $(y_1,y_2,x_i)\in{\mathcal{F}}$
,
$(y_1,y_2,x_i)\in{\mathcal{F}}$
,
![]() $i=1,2$
. Since
$i=1,2$
. Since
![]() $(x_1,x_2,y_2)\in{\mathcal{F}}$
and
$(x_1,x_2,y_2)\in{\mathcal{F}}$
and
![]() $(z,y_1)$
is 3-fold covered,
$(z,y_1)$
is 3-fold covered,
![]() $(z,y_1,x_1),(z,y_1,x_2)\in{\mathcal{F}}$
. Similarly,
$(z,y_1,x_1),(z,y_1,x_2)\in{\mathcal{F}}$
. Similarly,
![]() $(z,y_2,x_1),(z,y_2,x_2)\in{\mathcal{F}}$
. Hence
$(z,y_2,x_1),(z,y_2,x_2)\in{\mathcal{F}}$
. Hence
![]() $\{x_1,x_2,y_1,y_2,z\}$
spans a complete 3-graph in
$\{x_1,x_2,y_1,y_2,z\}$
spans a complete 3-graph in
![]() $\mathcal{F}$
. Since
$\mathcal{F}$
. Since
![]() $\mathcal{F}$
is intersecting, we conclude that
$\mathcal{F}$
is intersecting, we conclude that
![]() ${\mathcal{F}}=\binom{[5]}{3}$
up to isomorphism and
${\mathcal{F}}=\binom{[5]}{3}$
up to isomorphism and
![]() $|{\mathcal{F}}^*|=10$
. Suppose next that there are two edges intersecting in two vertices say
$|{\mathcal{F}}^*|=10$
. Suppose next that there are two edges intersecting in two vertices say
![]() $(x,z_1,z_2),(y,z_1,z_2)\in{\mathcal{F}}^*$
, since
$(x,z_1,z_2),(y,z_1,z_2)\in{\mathcal{F}}^*$
, since
![]() $(x,z_1),(y,z_2)$
are 3-fold covered and
$(x,z_1),(y,z_2)$
are 3-fold covered and
![]() $\mathcal{F}$
is intersecting, there exists
$\mathcal{F}$
is intersecting, there exists
![]() $w$
such that
$w$
such that
![]() $(x,z_1,y),(y,z_2,x),(x,z_1,w),(y,z_2,w)\in{\mathcal{F}}$
. Arguing with
$(x,z_1,y),(y,z_2,x),(x,z_1,w),(y,z_2,w)\in{\mathcal{F}}$
. Arguing with
![]() $(x,z_2)$
and
$(x,z_2)$
and
![]() $(y,z_1)$
, we infer that
$(y,z_1)$
, we infer that
![]() $(x,z_2,y),(y,z_1,x),(x,z_2,w),(y,z_1,w)\in{\mathcal{F}}$
. Hence
$(x,z_2,y),(y,z_1,x),(x,z_2,w),(y,z_1,w)\in{\mathcal{F}}$
. Hence
![]() $\{x,y,z_1,z_2,w\}$
spans a complete 3-graph in
$\{x,y,z_1,z_2,w\}$
spans a complete 3-graph in
![]() $\mathcal{F}$
. Since
$\mathcal{F}$
. Since
![]() $\mathcal{F}$
is intersecting, we conclude that
$\mathcal{F}$
is intersecting, we conclude that
![]() ${\mathcal{F}}=\binom{[5]}{3}$
up to isomorphism and
${\mathcal{F}}=\binom{[5]}{3}$
up to isomorphism and
![]() $|{\mathcal{F}}^*|=10$
. If
$|{\mathcal{F}}^*|=10$
. If
![]() ${\mathcal{F}}^*$
is 3-intersecting, then
${\mathcal{F}}^*$
is 3-intersecting, then
![]() $|{\mathcal{F}}^*|\leq 1$
holds trivially.
$|{\mathcal{F}}^*|\leq 1$
holds trivially.
For
![]() $r\geq 4$
, we claim that each member in
$r\geq 4$
, we claim that each member in
![]() $\partial{{\mathcal{F}}^*}$
is a transversal of
$\partial{{\mathcal{F}}^*}$
is a transversal of
![]() $\mathcal{F}$
. Otherwise, let
$\mathcal{F}$
. Otherwise, let
![]() $G\in \partial{{\mathcal{F}}^*}$
be a
$G\in \partial{{\mathcal{F}}^*}$
be a
![]() $2$
-set that is not a transversal. Then there exists
$2$
-set that is not a transversal. Then there exists
![]() $F\subset{\mathcal{F}}$
such that
$F\subset{\mathcal{F}}$
such that
![]() $F\cap G=\emptyset$
. Since
$F\cap G=\emptyset$
. Since
![]() $G\in \partial{\mathcal{F}}^*$
and
$G\in \partial{\mathcal{F}}^*$
and
![]() $r\geq 4\gt |F|$
, there exists
$r\geq 4\gt |F|$
, there exists
![]() $x$
such that
$x$
such that
![]() $G\cup \{x\}\in{\mathcal{F}}$
and
$G\cup \{x\}\in{\mathcal{F}}$
and
![]() $F\cap (G\cup \{x\})=\emptyset$
, a contradiction.
$F\cap (G\cup \{x\})=\emptyset$
, a contradiction.
Thus
![]() $\partial{{\mathcal{F}}^*}\subset{\mathcal{T}}({\mathcal{F}})$
. By Lemma 5.1 (i)
$\partial{{\mathcal{F}}^*}\subset{\mathcal{T}}({\mathcal{F}})$
. By Lemma 5.1 (i)
![]() $\partial{{\mathcal{F}}^*}$
is intersecting. In view of Proposition 5.3,
$\partial{{\mathcal{F}}^*}$
is intersecting. In view of Proposition 5.3,
![]() ${\mathcal{F}}^*$
is 3-intersecting. For
${\mathcal{F}}^*$
is 3-intersecting. For
![]() $n\geq 6$
, by Proposition 5.3 and (1) we have
$n\geq 6$
, by Proposition 5.3 and (1) we have
![]() $|{\mathcal{F}}^*|\leq \binom{n-3}{3-3}=1$
. In the case of equality, by symmetry we may assume that
$|{\mathcal{F}}^*|\leq \binom{n-3}{3-3}=1$
. In the case of equality, by symmetry we may assume that
![]() ${\mathcal{F}}^*=[3]$
.
${\mathcal{F}}^*=[3]$
.
Then we claim
![]() $|F\cap [3]|\geq 2$
for all
$|F\cap [3]|\geq 2$
for all
![]() $F\in{\mathcal{F}}$
. Indeed, otherwise
$F\in{\mathcal{F}}$
. Indeed, otherwise
![]() $|F\cap [3]|=1$
for some
$|F\cap [3]|=1$
for some
![]() $F\in{\mathcal{F}}$
, without loss of generality assume
$F\in{\mathcal{F}}$
, without loss of generality assume
![]() $F\cap [3]=\{1\}$
, then we can find an
$F\cap [3]=\{1\}$
, then we can find an
![]() $F'\in{\mathcal{F}}$
disjoint to
$F'\in{\mathcal{F}}$
disjoint to
![]() $F$
since
$F$
since
![]() $(2,3)$
is
$(2,3)$
is
![]() $r$
-fold covered with
$r$
-fold covered with
![]() $r\geq 4\gt |F|$
, a contradiction. Thus
$r\geq 4\gt |F|$
, a contradiction. Thus
![]() $|F\cap [3]|\geq 2$
for all
$|F\cap [3]|\geq 2$
for all
![]() $F\in{\mathcal{F}}$
. Using that
$F\in{\mathcal{F}}$
. Using that
![]() $\mathcal{F}$
is saturated, we conclude that
$\mathcal{F}$
is saturated, we conclude that
![]() ${\mathcal{F}}={\mathcal{L}}(n,3,2)$
up to isomorphism. For
${\mathcal{F}}={\mathcal{L}}(n,3,2)$
up to isomorphism. For
![]() $n\leq 5$
, clearly
$n\leq 5$
, clearly
![]() ${\mathcal{F}}\subset \binom{[5]}{3}$
. Since no 2-set is contained in 4 or more 3-sets in
${\mathcal{F}}\subset \binom{[5]}{3}$
. Since no 2-set is contained in 4 or more 3-sets in
![]() $\binom{[5]}{3}$
, we have
$\binom{[5]}{3}$
, we have
![]() $|{\mathcal{F}}^*|=0$
.
$|{\mathcal{F}}^*|=0$
.
The following proposition proves Theorem 1.8 for
![]() $3\leq r\leq k-1$
and
$3\leq r\leq k-1$
and
![]() $n\geq n_0(k,r)$
.
$n\geq n_0(k,r)$
.
Proposition 5.5.
![]() $f^*(n,k,r) =\binom{n-3}{k-3}+O(n^{k-r})$
for
$f^*(n,k,r) =\binom{n-3}{k-3}+O(n^{k-r})$
for
![]() $4\leq r\leq k-1$
and
$4\leq r\leq k-1$
and
![]() $n\geq n_0(k,r)$
;
$n\geq n_0(k,r)$
;
![]() $f^*(n,k,3) =|{\mathcal{L}}(n,k,3)|$
for
$f^*(n,k,3) =|{\mathcal{L}}(n,k,3)|$
for
![]() $n\geq n_0(k)$
.
$n\geq n_0(k)$
.
Proof. Let
![]() ${\mathcal{F}}\subset \binom{[n]}{k}$
be a saturated intersecting family and let
${\mathcal{F}}\subset \binom{[n]}{k}$
be a saturated intersecting family and let
![]() ${\mathcal{F}}^*$
be the family of
${\mathcal{F}}^*$
be the family of
![]() $r$
-complete sets in
$r$
-complete sets in
![]() $\mathcal{F}$
. Let
$\mathcal{F}$
. Let
![]() ${\mathcal{B}}={\mathcal{B}}({\mathcal{F}})$
and
${\mathcal{B}}={\mathcal{B}}({\mathcal{F}})$
and
![]() $X=\mathop{\cup }\limits _{B\in{\mathcal{B}}} B$
. By Lemma 5.2, we have
$X=\mathop{\cup }\limits _{B\in{\mathcal{B}}} B$
. By Lemma 5.2, we have
![]() $|X|\leq k\cdot k^k=k^{k+1}$
. Let
$|X|\leq k\cdot k^k=k^{k+1}$
. Let
If
![]() $p\geq 4$
, then for
$p\geq 4$
, then for
![]() $n\geq n_0(k,r)$
we have
$n\geq n_0(k,r)$
we have
 \begin{equation*} |{\mathcal {F}}^*|\leq \sum _{4\leq i\leq k} \binom {|X|}{i}\binom {n-|X|}{k-i}\leq \sum _{4\leq i\leq k} \binom {k^{k+1}}{i}\binom {n-k^{k+1}}{k-i} \leq 2\binom {k^{k+1}}{4}\binom {n-6}{k-4}\lt \binom {n-3}{k-3} \end{equation*}
\begin{equation*} |{\mathcal {F}}^*|\leq \sum _{4\leq i\leq k} \binom {|X|}{i}\binom {n-|X|}{k-i}\leq \sum _{4\leq i\leq k} \binom {k^{k+1}}{i}\binom {n-k^{k+1}}{k-i} \leq 2\binom {k^{k+1}}{4}\binom {n-6}{k-4}\lt \binom {n-3}{k-3} \end{equation*}
and we are done. If
![]() $p=1$
, then there exists
$p=1$
, then there exists
![]() $F^*\in{\mathcal{F}}^*$
such that
$F^*\in{\mathcal{F}}^*$
such that
![]() $F^*\cap X=\{x\}$
. It follows that
$F^*\cap X=\{x\}$
. It follows that
![]() $\{x\}\in{\mathcal{B}}$
. By saturatedness we have
$\{x\}\in{\mathcal{B}}$
. By saturatedness we have
![]() ${\mathcal{F}}={\mathcal{S}}_x$
and
${\mathcal{F}}={\mathcal{S}}_x$
and
![]() $|{\mathcal{F}}^*|=0$
. If
$|{\mathcal{F}}^*|=0$
. If
![]() $p=2$
then for some
$p=2$
then for some
![]() $F^*\in{\mathcal{F}}^*$
,
$F^*\in{\mathcal{F}}^*$
,
![]() $F^*\cap X=\{x,y\}\in{\mathcal{B}}$
. Using
$F^*\cap X=\{x,y\}\in{\mathcal{B}}$
. Using
![]() $r$
-completeness we find
$r$
-completeness we find
![]() $F_x\in{\mathcal{F}}$
,
$F_x\in{\mathcal{F}}$
,
![]() $F_x\supset F^*\setminus \{y\}$
and
$F_x\supset F^*\setminus \{y\}$
and
![]() $F_y\in{\mathcal{F}}$
,
$F_y\in{\mathcal{F}}$
,
![]() $F_y\supset F^*\setminus \{x\}$
and
$F_y\supset F^*\setminus \{x\}$
and
![]() $F_x\cap F_y\cap X=\emptyset$
, contradicting (22). Thus we may assume
$F_x\cap F_y\cap X=\emptyset$
, contradicting (22). Thus we may assume
![]() $p=3$
.
$p=3$
.
Define the 3-graph
Note that
![]() $p=3$
implies
$p=3$
implies
![]() ${\mathcal{T}}\neq \emptyset$
. By (22) we infer that
${\mathcal{T}}\neq \emptyset$
. By (22) we infer that
![]() $\mathcal{T}$
is intersecting. We distinguish two cases.
$\mathcal{T}$
is intersecting. We distinguish two cases.
Case 1.
![]() $r=3$
.
$r=3$
.
If there exist
![]() $(x_1,y_1,z), (x_2,y_2,z)\in{\mathcal{T}}^*$
, let
$(x_1,y_1,z), (x_2,y_2,z)\in{\mathcal{T}}^*$
, let
![]() $H_i\in \binom{[n]\setminus X}{k-3}$
such that
$H_i\in \binom{[n]\setminus X}{k-3}$
such that
![]() $H_i\cup \{x_i,y_i,z\}\in{\mathcal{F}}^*$
,
$H_i\cup \{x_i,y_i,z\}\in{\mathcal{F}}^*$
,
![]() $i=1,2$
. By 3-completeness and (22), we have
$i=1,2$
. By 3-completeness and (22), we have
Then there exists
![]() $H_3\in \binom{[n]\setminus X}{k-3}$
such that
$H_3\in \binom{[n]\setminus X}{k-3}$
such that
![]() $H_3\cup \{x_1,y_1,x_2\}\in{\mathcal{F}}$
. Since
$H_3\cup \{x_1,y_1,x_2\}\in{\mathcal{F}}$
. Since
![]() $H_2\cup \{y_2,z\}$
is covered by at least 3 members of
$H_2\cup \{y_2,z\}$
is covered by at least 3 members of
![]() $\mathcal{F}$
, by (22) we infer
$\mathcal{F}$
, by (22) we infer
![]() $H_2\cup (x_1,y_2,z),H_2\cup (y_1,y_2,z)\in{\mathcal{F}}$
. Similarly, we have
$H_2\cup (x_1,y_2,z),H_2\cup (y_1,y_2,z)\in{\mathcal{F}}$
. Similarly, we have
![]() $H_2\cup (x_2,y_1,z),H_2\cup (x_1,x_2,z)\in{\mathcal{F}}$
. Hence
$H_2\cup (x_2,y_1,z),H_2\cup (x_1,x_2,z)\in{\mathcal{F}}$
. Hence
![]() $\{x_1,x_2,y_1,y_2,z\}$
spans a complete 3-graph in
$\{x_1,x_2,y_1,y_2,z\}$
spans a complete 3-graph in
![]() $\mathcal{T}$
. We claim that
$\mathcal{T}$
. We claim that
![]() $|F\cap \{x_1,x_2,y_1,y_2,z\}|\geq 3$
for all
$|F\cap \{x_1,x_2,y_1,y_2,z\}|\geq 3$
for all
![]() $F\in{\mathcal{F}}$
. Indeed, otherwise suppose that there is
$F\in{\mathcal{F}}$
. Indeed, otherwise suppose that there is
![]() $F\in{\mathcal{F}}$
with
$F\in{\mathcal{F}}$
with
![]() $|F\cap \{x_1,x_2,y_1,y_2,z\}|\leq 2$
. Without loss of generality assume that
$|F\cap \{x_1,x_2,y_1,y_2,z\}|\leq 2$
. Without loss of generality assume that
![]() $F\cap \{y_1,y_2,z\}=\emptyset$
. Since
$F\cap \{y_1,y_2,z\}=\emptyset$
. Since
![]() $\{y_1,y_2,z\}\in{\mathcal{T}}$
, there exists
$\{y_1,y_2,z\}\in{\mathcal{T}}$
, there exists
![]() $H\in \binom{[n]\setminus X}{k-3}$
such that
$H\in \binom{[n]\setminus X}{k-3}$
such that
![]() $H\cup \{y_1,y_2,z\}=:F'\in{\mathcal{F}}$
. But then
$H\cup \{y_1,y_2,z\}=:F'\in{\mathcal{F}}$
. But then
![]() $F\cap F'\cap X=\emptyset$
, contradicting (22). By saturatedness, we conclude that
$F\cap F'\cap X=\emptyset$
, contradicting (22). By saturatedness, we conclude that
![]() ${\mathcal{F}}={\mathcal{L}}(n,k,3)$
up to isomorphism and
${\mathcal{F}}={\mathcal{L}}(n,k,3)$
up to isomorphism and
![]() $|{\mathcal{F}}^*|= |{\mathcal{L}}(n,k,3)|$
.
$|{\mathcal{F}}^*|= |{\mathcal{L}}(n,k,3)|$
.
If there exist
![]() $(x_1,y,z), (x_2,y,z)\in{\mathcal{T}}^*$
, let
$(x_1,y,z), (x_2,y,z)\in{\mathcal{T}}^*$
, let
![]() $H_i\in \binom{[n]\setminus X}{k-3}$
such that
$H_i\in \binom{[n]\setminus X}{k-3}$
such that
![]() $H_i\cup \{x_i,y,z\}\in{\mathcal{F}}^*$
,
$H_i\cup \{x_i,y,z\}\in{\mathcal{F}}^*$
,
![]() $i=1,2$
. Since
$i=1,2$
. Since
![]() $H_1\cup \{x_1,y\},H_2\cup \{x_2,z\}$
are 3-fold covered, by (22) there exists
$H_1\cup \{x_1,y\},H_2\cup \{x_2,z\}$
are 3-fold covered, by (22) there exists
![]() $w\in X$
such that
$w\in X$
such that
![]() $H_1\cup \{x_1,y,x_2\},H_1\cup \{x_1,y,w\},H_2\cup \{x_2,z,x_1\},H_2\cup \{x_2,z,w\}\in{\mathcal{F}}$
. Similarly,
$H_1\cup \{x_1,y,x_2\},H_1\cup \{x_1,y,w\},H_2\cup \{x_2,z,x_1\},H_2\cup \{x_2,z,w\}\in{\mathcal{F}}$
. Similarly,
![]() $H_1\cup \{x_1,z,x_2\},H_1\cup \{x_1,z,w\},H_2\cup \{x_2,y,x_1\},H_2\cup \{x_2,y,w\}\in{\mathcal{F}}$
. Then
$H_1\cup \{x_1,z,x_2\},H_1\cup \{x_1,z,w\},H_2\cup \{x_2,y,x_1\},H_2\cup \{x_2,y,w\}\in{\mathcal{F}}$
. Then
![]() $\{x_1,x_2,y,z,w\}$
spans a complete 3-graph in
$\{x_1,x_2,y,z,w\}$
spans a complete 3-graph in
![]() $\mathcal{T}$
. By the same argument and saturatedness, we conclude that
$\mathcal{T}$
. By the same argument and saturatedness, we conclude that
![]() ${\mathcal{F}}={\mathcal{L}}(n,k,3)$
up to isomorphism and
${\mathcal{F}}={\mathcal{L}}(n,k,3)$
up to isomorphism and
![]() $|{\mathcal{F}}^*|= |{\mathcal{L}}(n,k,3)|$
.
$|{\mathcal{F}}^*|= |{\mathcal{L}}(n,k,3)|$
.
Now we may assume that
![]() ${\mathcal{T}}^*$
is 3-intersecting. Since
${\mathcal{T}}^*$
is 3-intersecting. Since
![]() ${\mathcal{T}}^*$
is a 3-graph, we trivially have
${\mathcal{T}}^*$
is a 3-graph, we trivially have
![]() $|{\mathcal{T}}^*|\leq 1$
. Then for
$|{\mathcal{T}}^*|\leq 1$
. Then for
![]() $n\geq n_0(k)$
we obtain that
$n\geq n_0(k)$
we obtain that
Case 2.
![]() $r\geq 4$
.
$r\geq 4$
.
Claim 6.
For all
![]() $F\in{\mathcal{F}}^*$
and
$F\in{\mathcal{F}}^*$
and
![]() $T\in{\mathcal{T}}^*$
,
$T\in{\mathcal{T}}^*$
,
Proof. Suppose the contrary. By symmetry let
![]() $T=\{1,2,3\}$
,
$T=\{1,2,3\}$
,
![]() $F\cap T=\{3\}$
(
$F\cap T=\{3\}$
(
![]() $F\cap T\neq \emptyset$
by (22)). By
$F\cap T\neq \emptyset$
by (22)). By
![]() $r$
-completeness there are distinct elements
$r$
-completeness there are distinct elements
![]() $y_1,\ldots,y_r$
such that
$y_1,\ldots,y_r$
such that
![]() $(F\setminus \{3\})\cup \{y_i\}\in{\mathcal{F}}$
. Since
$(F\setminus \{3\})\cup \{y_i\}\in{\mathcal{F}}$
. Since
![]() $r\geq 4$
, without loss of generality, assume
$r\geq 4$
, without loss of generality, assume
![]() $y_r\notin \{1,2,3\}$
. Then
$y_r\notin \{1,2,3\}$
. Then
![]() $((F\setminus \{3\})\cup \{y_r\})\cap T=\emptyset$
contradicting (22).
$((F\setminus \{3\})\cup \{y_r\})\cap T=\emptyset$
contradicting (22).
Claim 7.
![]() $|{\mathcal{T}}^*|=1$
.
$|{\mathcal{T}}^*|=1$
.
Proof. Otherwise using Claim 6, without loss of generality,
![]() $\{1,2,3\},\{1,2,4\}\in{\mathcal{T}}^*$
. Let
$\{1,2,3\},\{1,2,4\}\in{\mathcal{T}}^*$
. Let
![]() $H_i\in \binom{[n]\setminus X}{k-3}$
such that
$H_i\in \binom{[n]\setminus X}{k-3}$
such that
![]() $H_i\cup \{1,2,i\}\in{\mathcal{F}}^*$
,
$H_i\cup \{1,2,i\}\in{\mathcal{F}}^*$
,
![]() $i=3,4$
. Let
$i=3,4$
. Let
![]() $x_1,\ldots,x_r$
be such that
$x_1,\ldots,x_r$
be such that
![]() $H_3\cup \{1,3,x_j\}\in{\mathcal{F}}$
,
$H_3\cup \{1,3,x_j\}\in{\mathcal{F}}$
,
![]() $j=1,\ldots,r$
. Let
$j=1,\ldots,r$
. Let
![]() $y_1,\ldots,y_r$
be such that
$y_1,\ldots,y_r$
be such that
![]() $H_4\cup \{2,4,y_j\}\in{\mathcal{F}}$
,
$H_4\cup \{2,4,y_j\}\in{\mathcal{F}}$
,
![]() $j=1,\ldots,r$
. By
$j=1,\ldots,r$
. By
![]() $r\geq 4$
, without loss of generality assume
$r\geq 4$
, without loss of generality assume
![]() $x_1\notin \{2,4\}$
and
$x_1\notin \{2,4\}$
and
![]() $y_1\notin \{1,3,x_1\}$
. Then
$y_1\notin \{1,3,x_1\}$
. Then
contradicting (22).
By Claim 7, we may assume that
![]() ${\mathcal{T}}^*=\{(1,2,3)\}$
. Define
${\mathcal{T}}^*=\{(1,2,3)\}$
. Define
Claim 8.
![]() $F\in{\mathcal{F}}_i^*$
implies
$F\in{\mathcal{F}}_i^*$
implies
![]() $|F\cap X|\geq r$
,
$|F\cap X|\geq r$
,
![]() $i=1,2,3$
.
$i=1,2,3$
.
Proof. By symmetry assume
![]() $i=1$
and set
$i=1$
and set
![]() $S=F\cap X$
. Suppose indirectly
$S=F\cap X$
. Suppose indirectly
![]() $|S|\lt r$
. Let
$|S|\lt r$
. Let
![]() $\tilde{F}\in{\mathcal{F}}^*$
with
$\tilde{F}\in{\mathcal{F}}^*$
with
![]() $\tilde{F}\cap X=[3]$
. By
$\tilde{F}\cap X=[3]$
. By
![]() $r$
-completeness there are
$r$
-completeness there are
![]() $x_1,x_2,\ldots,x_r$
distinct elements with
$x_1,x_2,\ldots,x_r$
distinct elements with
![]() $(\tilde{F}\setminus \{3\})\cup \{x_j\}\in{\mathcal{F}}$
,
$(\tilde{F}\setminus \{3\})\cup \{x_j\}\in{\mathcal{F}}$
,
![]() $1\leq j\leq r$
. Also
$1\leq j\leq r$
. Also
![]() $F\setminus \{2\}$
is contained in
$F\setminus \{2\}$
is contained in
![]() $r\gt 3$
members of
$r\gt 3$
members of
![]() $\mathcal{F}$
. Let
$\mathcal{F}$
. Let
![]() $\hat{F}$
be one of them with
$\hat{F}$
be one of them with
![]() $\hat{F}\cap [3] = \{3\}$
and let
$\hat{F}\cap [3] = \{3\}$
and let
![]() $\hat{S}= \hat{F}\cap X$
. Clearly,
$\hat{S}= \hat{F}\cap X$
. Clearly,
![]() $|\hat{S}|\leq |S|\lt r$
. Consequently we can choose
$|\hat{S}|\leq |S|\lt r$
. Consequently we can choose
![]() $x_j\notin \hat{S}$
. Then
$x_j\notin \hat{S}$
. Then
contradicting (22).
 \begin{align*} |{\mathcal{F}}^*|&\leq |{\mathcal{T}}^*|\binom{n-|X|}{k-3}+\sum _{1\leq i\leq 3}|{\mathcal{F}}_i^*|\\[5pt] &\leq \binom{n-|X|}{k-3}+\sum _{r\leq i\leq k} \binom{3}{2}\binom{|X|}{i-2}\binom{n-|X|}{k-i}\\[5pt] &=\binom{n-3}{k-3}+O(n^{k-r}) \end{align*}
\begin{align*} |{\mathcal{F}}^*|&\leq |{\mathcal{T}}^*|\binom{n-|X|}{k-3}+\sum _{1\leq i\leq 3}|{\mathcal{F}}_i^*|\\[5pt] &\leq \binom{n-|X|}{k-3}+\sum _{r\leq i\leq k} \binom{3}{2}\binom{|X|}{i-2}\binom{n-|X|}{k-i}\\[5pt] &=\binom{n-3}{k-3}+O(n^{k-r}) \end{align*}
and the proposition is proven.
6. Maximizing the number of
 $k$
-complete sets in an intersecting family
$k$
-complete sets in an intersecting family
In this section, we prove Theorem 1.8 for
![]() $r\geq k$
. By using Bollobás Set-pairs Inequality (Theorem 2.3) and the Hilton-Milner-Frankl Theorem, we determine
$r\geq k$
. By using Bollobás Set-pairs Inequality (Theorem 2.3) and the Hilton-Milner-Frankl Theorem, we determine
![]() $f^*(n,k,k)$
for
$f^*(n,k,k)$
for
![]() $k\geq 5$
and
$k\geq 5$
and
![]() $n\geq n_0(k)$
. The cases
$n\geq n_0(k)$
. The cases
![]() $r\geq k+1$
and
$r\geq k+1$
and
![]() $r=k=4$
of Theorem 1.8 will be proved separately.
$r=k=4$
of Theorem 1.8 will be proved separately.
First we show that if an intersecting family contains a relatively
![]() $k$
-complete sunflower of given shape, then Theorem 1.8 holds.
$k$
-complete sunflower of given shape, then Theorem 1.8 holds.
Lemma 6.1.
Let
![]() ${\mathcal{F}}\subset \binom{[n]}{k}$
be an intersecting family and let
${\mathcal{F}}\subset \binom{[n]}{k}$
be an intersecting family and let
![]() ${\mathcal{F}}^*$
be the family of
${\mathcal{F}}^*$
be the family of
![]() $k$
-complete sets in
$k$
-complete sets in
![]() $\mathcal{F}$
. If
$\mathcal{F}$
. If
![]() ${\mathcal{F}}^*$
contains a sunflower with
${\mathcal{F}}^*$
contains a sunflower with
![]() $k+1$
petals and centre
$k+1$
petals and centre
![]() $C$
of size
$C$
of size
![]() $3$
and
$3$
and
![]() $k\geq 4$
, then
$k\geq 4$
, then
![]() $C\subset F$
for all
$C\subset F$
for all
![]() $F\in{\mathcal{F}}^*$
. In particular,
$F\in{\mathcal{F}}^*$
. In particular,
Proof. Suppose that
![]() $F_1,F_2,\ldots,F_{k+1}$
is a sunflower in
$F_1,F_2,\ldots,F_{k+1}$
is a sunflower in
![]() ${\mathcal{F}}^*$
with centre
${\mathcal{F}}^*$
with centre
![]() $[3]$
and let
$[3]$
and let
![]() $G_i=F_i\setminus [3]$
,
$G_i=F_i\setminus [3]$
,
![]() $i=1,\ldots,k+1$
.
$i=1,\ldots,k+1$
.
If there exists
![]() $F\in{\mathcal{F}}^*$
with
$F\in{\mathcal{F}}^*$
with
![]() $|F\cap [3]|\leq 1$
, pick
$|F\cap [3]|\leq 1$
, pick
![]() $G\in \binom{F}{k-1}$
with
$G\in \binom{F}{k-1}$
with
![]() $G\cap [3]=\emptyset$
. Then
$G\cap [3]=\emptyset$
. Then
![]() $G\cap F_i\neq \emptyset$
can hold for at most
$G\cap F_i\neq \emptyset$
can hold for at most
![]() $k-1$
values of
$k-1$
values of
![]() $i$
. Pick
$i$
. Pick
![]() $F_p,F_r$
disjoint to
$F_p,F_r$
disjoint to
![]() $G$
. Now
$G$
. Now
![]() $k$
-completeness and
$k$
-completeness and
![]() $k\geq 4$
imply that we can choose
$k\geq 4$
imply that we can choose
![]() $z\notin [3]$
,
$z\notin [3]$
,
![]() $G\cup \{z\}\in{\mathcal{F}}$
. Then either
$G\cup \{z\}\in{\mathcal{F}}$
. Then either
![]() $F_p$
or
$F_p$
or
![]() $F_r$
is disjoint to
$F_r$
is disjoint to
![]() $G\cup \{z\}$
, a contradiction.
$G\cup \{z\}$
, a contradiction.
If there exists
![]() $F\in{\mathcal{F}}^*$
with
$F\in{\mathcal{F}}^*$
with
![]() $|F\cap [3]|= 2$
, without loss of generality, assume that
$|F\cap [3]|= 2$
, without loss of generality, assume that
![]() $F\cap [3]= \{1,2\}$
and let
$F\cap [3]= \{1,2\}$
and let
![]() $G=F\setminus \{1,2\}$
. Pick
$G=F\setminus \{1,2\}$
. Pick
![]() $F_p,F_q,F_r$
disjoint to
$F_p,F_q,F_r$
disjoint to
![]() $G$
. Since
$G$
. Since
![]() $k\geq 4$
, we can choose
$k\geq 4$
, we can choose
![]() $z,w\notin [3]$
such that
$z,w\notin [3]$
such that
![]() $G\cup \{1,z\},G\cup \{1,w\}\in{\mathcal{F}}$
. Then one of
$G\cup \{1,z\},G\cup \{1,w\}\in{\mathcal{F}}$
. Then one of
![]() $F_p, F_q, F_r$
, without loss of generality say
$F_p, F_q, F_r$
, without loss of generality say
![]() $F_p$
, is disjoint to both
$F_p$
, is disjoint to both
![]() $G\cup \{z\}$
and
$G\cup \{z\}$
and
![]() $G\cup \{w\}$
. Since
$G\cup \{w\}$
. Since
![]() $F_p\setminus \{1\}$
is covered by at least
$F_p\setminus \{1\}$
is covered by at least
![]() $k$
members of
$k$
members of
![]() $\mathcal{F}$
, we can find
$\mathcal{F}$
, we can find
![]() $u\notin G\cup \{1\}$
such that
$u\notin G\cup \{1\}$
such that
![]() $(F_p\setminus \{1\})\cup \{u\}\in{\mathcal{F}}$
. Then either
$(F_p\setminus \{1\})\cup \{u\}\in{\mathcal{F}}$
. Then either
![]() $z\neq u$
or
$z\neq u$
or
![]() $w\neq u$
holds. Without loss of generality, assume that
$w\neq u$
holds. Without loss of generality, assume that
![]() $z\neq u$
, then
$z\neq u$
, then
![]() $(F_p\setminus \{1\})\cup \{u\}$
and
$(F_p\setminus \{1\})\cup \{u\}$
and
![]() $G\cup \{1,z\}$
are disjoint, a contradiction. Thus,
$G\cup \{1,z\}$
are disjoint, a contradiction. Thus,
![]() $[3]\subset F$
for all
$[3]\subset F$
for all
![]() $F\in{\mathcal{F}}^*$
and the lemma follows.
$F\in{\mathcal{F}}^*$
and the lemma follows.
We prove Theorem 1.8 for
![]() $r\geq k+1$
and
$r\geq k+1$
and
![]() $k\geq 4$
by the following proposition.
$k\geq 4$
by the following proposition.
Proposition 6.2.
![]() $f^*(n,k,r) = \binom{n-3}{k-3}$
for
$f^*(n,k,r) = \binom{n-3}{k-3}$
for
![]() $r\geq k+1$
and
$r\geq k+1$
and
![]() $n\geq \max \{4(k-2),k+r-1\}$
.
$n\geq \max \{4(k-2),k+r-1\}$
.
Proof. Let
![]() ${\mathcal{F}}\subset \binom{[n]}{k}$
be a saturated intersecting family. Let
${\mathcal{F}}\subset \binom{[n]}{k}$
be a saturated intersecting family. Let
![]() ${\mathcal{F}}^*$
be the family of
${\mathcal{F}}^*$
be the family of
![]() $r$
-complete sets in
$r$
-complete sets in
![]() $\mathcal{F}$
and let
$\mathcal{F}$
and let
![]() ${\mathcal{G}}=\partial{{\mathcal{F}}^*}$
. We claim that each member in
${\mathcal{G}}=\partial{{\mathcal{F}}^*}$
. We claim that each member in
![]() $\mathcal{G}$
is a transversal of
$\mathcal{G}$
is a transversal of
![]() $\mathcal{F}$
. Otherwise, let
$\mathcal{F}$
. Otherwise, let
![]() $G\in{\mathcal{G}}$
be a
$G\in{\mathcal{G}}$
be a
![]() $(k-1)$
-set that is not a transversal. Then there exists
$(k-1)$
-set that is not a transversal. Then there exists
![]() $F\subset{\mathcal{F}}$
such that
$F\subset{\mathcal{F}}$
such that
![]() $F\cap G=\emptyset$
. Since
$F\cap G=\emptyset$
. Since
![]() $G\in \partial{\mathcal{F}}^*$
and
$G\in \partial{\mathcal{F}}^*$
and
![]() $r\gt |F|$
, there exists
$r\gt |F|$
, there exists
![]() $x$
such that
$x$
such that
![]() $G\cup \{x\}\in{\mathcal{F}}$
and
$G\cup \{x\}\in{\mathcal{F}}$
and
![]() $F\cap (G\cup \{x\})=\emptyset$
, a contradiction. Thus
$F\cap (G\cup \{x\})=\emptyset$
, a contradiction. Thus
![]() ${\mathcal{G}}\subset{\mathcal{T}}({\mathcal{F}})$
.
${\mathcal{G}}\subset{\mathcal{T}}({\mathcal{F}})$
.
Since
![]() $\mathcal{F}$
is saturated, all
$\mathcal{F}$
is saturated, all
![]() $k$
-element supersets of any
$k$
-element supersets of any
![]() $G\in{\mathcal{T}}({\mathcal{F}})$
are members of
$G\in{\mathcal{T}}({\mathcal{F}})$
are members of
![]() $\mathcal{F}$
. By Lemma 5.1 (i) we see that
$\mathcal{F}$
. By Lemma 5.1 (i) we see that
![]() $\mathcal{G}$
is intersecting. In view of Proposition 5.3,
$\mathcal{G}$
is intersecting. In view of Proposition 5.3,
![]() ${\mathcal{F}}^*$
is 3-intersecting. Since
${\mathcal{F}}^*$
is 3-intersecting. Since
![]() $n\geq 4(k-2)$
, by (1) we have
$n\geq 4(k-2)$
, by (1) we have
![]() $|{\mathcal{F}}^*|\leq \binom{n-3}{k-3}$
.
$|{\mathcal{F}}^*|\leq \binom{n-3}{k-3}$
.
By using the Bollobás Set-pairs Theorem and the Hilton-Milner-Frankl Theorem, we prove Theorem 1.8 for
![]() $r=k$
and
$r=k$
and
![]() $k\geq 5$
.
$k\geq 5$
.
Proposition 6.3.
![]() $f^*(n,k,k) = \binom{n-3}{k-3}$
for
$f^*(n,k,k) = \binom{n-3}{k-3}$
for
![]() $r= k\geq 5$
and
$r= k\geq 5$
and
![]() $n\geq k^3\binom{2k-1}{k}$
.
$n\geq k^3\binom{2k-1}{k}$
.
Proof. Let
![]() ${\mathcal{F}}\subset \binom{[n]}{k}$
be a saturated intersecting family. Let
${\mathcal{F}}\subset \binom{[n]}{k}$
be a saturated intersecting family. Let
![]() ${\mathcal{F}}^*$
be the family of
${\mathcal{F}}^*$
be the family of
![]() $k$
-complete sets in
$k$
-complete sets in
![]() $\mathcal{F}$
and let
$\mathcal{F}$
and let
![]() ${\mathcal{G}}=\partial{{\mathcal{F}}^*}$
. Define
${\mathcal{G}}=\partial{{\mathcal{F}}^*}$
. Define
Claim 9.
To every
![]() $G\in{\mathcal{G}}'$
there is a unique
$G\in{\mathcal{G}}'$
there is a unique
![]() $k$
-element set
$k$
-element set
![]() $H(G)\in{\mathcal{F}}$
which is disjoint to
$H(G)\in{\mathcal{F}}$
which is disjoint to
![]() $G$
.
$G$
.
Proof. Let
![]() $G\cup \{x_i\}\in{\mathcal{F}}$
,
$G\cup \{x_i\}\in{\mathcal{F}}$
,
![]() $i=1,\ldots,k$
, the existence of
$i=1,\ldots,k$
, the existence of
![]() $x_i$
is guaranteed by
$x_i$
is guaranteed by
![]() $k$
-completeness. Since
$k$
-completeness. Since
![]() $G\notin{\mathcal{T}}({\mathcal{F}})$
, there is
$G\notin{\mathcal{T}}({\mathcal{F}})$
, there is
![]() $F\in{\mathcal{F}}$
satisfying
$F\in{\mathcal{F}}$
satisfying
![]() $G\cap F=\emptyset$
. As
$G\cap F=\emptyset$
. As
![]() $\mathcal{F}$
is intersecting,
$\mathcal{F}$
is intersecting,
![]() $F\cap (G\cup \{x_i\})=\{x_i\}$
for
$F\cap (G\cup \{x_i\})=\{x_i\}$
for
![]() $1\leq i\leq k$
. Using
$1\leq i\leq k$
. Using
![]() $|F|=k$
,
$|F|=k$
,
![]() $F=\{x_1,\ldots,x_k\}=:H(G)$
is the unique possibility.
$F=\{x_1,\ldots,x_k\}=:H(G)$
is the unique possibility.
From Claim 9 it is clear that
![]() $H(G)\neq H(G')$
imply
$H(G)\neq H(G')$
imply
![]() $G\cap H(G')\neq \emptyset$
. Define
$G\cap H(G')\neq \emptyset$
. Define
Let
![]() ${\mathcal{H}}=\{H_1,\ldots,H_m\}$
. To each
${\mathcal{H}}=\{H_1,\ldots,H_m\}$
. To each
![]() $H_i\in{\mathcal{H}}$
, fix
$H_i\in{\mathcal{H}}$
, fix
![]() $G_i\in{\mathcal{G}}'$
satisfying
$G_i\in{\mathcal{G}}'$
satisfying
![]() $H(G_i)=H_i$
. Now
$H(G_i)=H_i$
. Now
![]() $H_i\cap G_j=\emptyset$
iff
$H_i\cap G_j=\emptyset$
iff
![]() $i=j$
, By (9), we obtain
$i=j$
, By (9), we obtain
For each
![]() $H\in{\mathcal{H}}$
, let
$H\in{\mathcal{H}}$
, let
Claim 10.
For each
![]() $H\in{\mathcal{H}}$
,
$H\in{\mathcal{H}}$
,
![]() ${\mathcal{G}}'(H)$
is 2-intersecting.
${\mathcal{G}}'(H)$
is 2-intersecting.
Proof. Suppose that there exist
![]() $G_1,G_2\in{\mathcal{G}}'(H)$
with
$G_1,G_2\in{\mathcal{G}}'(H)$
with
![]() $G_1\cap G_2=\{x\}$
. Let
$G_1\cap G_2=\{x\}$
. Let
![]() $H=\{x_1,\ldots,x_k\}$
. Since
$H=\{x_1,\ldots,x_k\}$
. Since
![]() $G_1\in \partial{\mathcal{F}}^*$
, there is
$G_1\in \partial{\mathcal{F}}^*$
, there is
![]() $F_1=G_1\cup \{x_i\}$
such that
$F_1=G_1\cup \{x_i\}$
such that
![]() $F_1\in{\mathcal{F}}^*$
. By symmetry we assume that
$F_1\in{\mathcal{F}}^*$
. By symmetry we assume that
![]() $i=1$
. By
$i=1$
. By
![]() $k$
-completeness, we have
$k$
-completeness, we have
![]() $(F_1\setminus \{x\})\cup \{y_p\}\in{\mathcal{F}}$
for
$(F_1\setminus \{x\})\cup \{y_p\}\in{\mathcal{F}}$
for
![]() $p=1,\ldots,k$
. Since
$p=1,\ldots,k$
. Since
![]() $|\{y_1,\ldots,y_k\}|\gt |G_2|$
, there exist
$|\{y_1,\ldots,y_k\}|\gt |G_2|$
, there exist
![]() $y_{p_0}\notin G_2$
. Since
$y_{p_0}\notin G_2$
. Since
![]() $k\geq 3$
, we may assume that
$k\geq 3$
, we may assume that
![]() $x_2\neq y_{p_0}$
. Then
$x_2\neq y_{p_0}$
. Then
![]() $G_1\cup \{x_1, y_{p_0}\}\setminus \{x\}$
,
$G_1\cup \{x_1, y_{p_0}\}\setminus \{x\}$
,
![]() $G_2\cup \{x_2\}$
are disjoint, a contradiction.
$G_2\cup \{x_2\}$
are disjoint, a contradiction.
Now we distinguish two cases.
Case 1. There exists
![]() $H\in{\mathcal{H}}$
such that
$H\in{\mathcal{H}}$
such that
![]() $|{\mathcal{G}}'(H)|\gt k(k-1)\binom{n-4}{k-4}$
.
$|{\mathcal{G}}'(H)|\gt k(k-1)\binom{n-4}{k-4}$
.
Since
![]() ${\mathcal{G}}'(H)$
is a 2-intersecting
${\mathcal{G}}'(H)$
is a 2-intersecting
![]() $(k-1)$
-graph, by (11)
$(k-1)$
-graph, by (11)
![]() ${\mathcal{G}}'(H)$
is a 2-star. So let
${\mathcal{G}}'(H)$
is a 2-star. So let
![]() ${\mathcal{G}}'(H)$
be a star with centre
${\mathcal{G}}'(H)$
be a star with centre
![]() $\{1,2\}$
. Let
$\{1,2\}$
. Let
![]() $H=\{x_1,\ldots,x_k\}$
. Define
$H=\{x_1,\ldots,x_k\}$
. Define
Note that
![]() ${\mathcal{G}}'(H)={\mathcal{G}}_1^H \cup \ldots \cup{\mathcal{G}}_k^H$
. Without loss of generality, we may assume that
${\mathcal{G}}'(H)={\mathcal{G}}_1^H \cup \ldots \cup{\mathcal{G}}_k^H$
. Without loss of generality, we may assume that
![]() $|{\mathcal{G}}_1^H| \geq \ldots \geq |{\mathcal{G}}_k^H|$
.
$|{\mathcal{G}}_1^H| \geq \ldots \geq |{\mathcal{G}}_k^H|$
.
Claim 11.
![]() ${\mathcal{G}}_2^H = \cdots ={\mathcal{G}}_k^H=\emptyset$
.
${\mathcal{G}}_2^H = \cdots ={\mathcal{G}}_k^H=\emptyset$
.
Proof. Suppose for contradiction that
![]() ${\mathcal{G}}_2^H \neq \emptyset$
and let
${\mathcal{G}}_2^H \neq \emptyset$
and let
![]() $ R_2\in{\mathcal{G}}_2^H([2])$
. Since
$ R_2\in{\mathcal{G}}_2^H([2])$
. Since
we have
 \begin{align*} \left |{\mathcal{G}}_1^H([2])\cap \binom{[n]\setminus R_2}{k-3}\right |&\geq |{\mathcal{G}}_1^H([2])|-|R_2|\binom{n-k-3}{k-4}\\[5pt] &\geq (k-1)\binom{n-4}{k-4} -(k-3)\binom{n-4}{k-4}\\[5pt] &=2\binom{n-4}{k-4}. \end{align*}
\begin{align*} \left |{\mathcal{G}}_1^H([2])\cap \binom{[n]\setminus R_2}{k-3}\right |&\geq |{\mathcal{G}}_1^H([2])|-|R_2|\binom{n-k-3}{k-4}\\[5pt] &\geq (k-1)\binom{n-4}{k-4} -(k-3)\binom{n-4}{k-4}\\[5pt] &=2\binom{n-4}{k-4}. \end{align*}
By (10) we have
![]() $\nu ({\mathcal{G}}_1^H([2])\cap \binom{[n]\setminus R_2}{k-3})\geq 2$
. It follows that there are
$\nu ({\mathcal{G}}_1^H([2])\cap \binom{[n]\setminus R_2}{k-3})\geq 2$
. It follows that there are
![]() $R_0, R_1\in{\mathcal{G}}_1^H([2])$
such that
$R_0, R_1\in{\mathcal{G}}_1^H([2])$
such that
![]() $R_0, R_1,R_2$
are pairwise disjoint sets. Set
$R_0, R_1,R_2$
are pairwise disjoint sets. Set
![]() $G_i=R_i\cup [2]$
for
$G_i=R_i\cup [2]$
for
![]() $i=0,1,2$
. Since
$i=0,1,2$
. Since
![]() $G_1\cup \{x_1\},\ G_2\cup \{x_2\}\in{\mathcal{F}}^*$
, we know that
$G_1\cup \{x_1\},\ G_2\cup \{x_2\}\in{\mathcal{F}}^*$
, we know that
![]() $E_1=R_1\cup \{1,x_1\}$
,
$E_1=R_1\cup \{1,x_1\}$
,
![]() $E_2=R_2\cup \{2,x_2\}$
are both covered by
$E_2=R_2\cup \{2,x_2\}$
are both covered by
![]() $k$
members of
$k$
members of
![]() $\mathcal{F}$
. To avoid disjointness, we have
$\mathcal{F}$
. To avoid disjointness, we have
![]() $E_1\cup \{y_2\}\in{\mathcal{F}}$
for each
$E_1\cup \{y_2\}\in{\mathcal{F}}$
for each
![]() $y_2\in E_2$
and
$y_2\in E_2$
and
![]() $E_2\cup \{y_1\}\in{\mathcal{F}}$
for each
$E_2\cup \{y_1\}\in{\mathcal{F}}$
for each
![]() $y_1\in E_1$
. Moreover, there is an extra element
$y_1\in E_1$
. Moreover, there is an extra element
![]() $z$
such that
$z$
such that
![]() $E_1\cup \{z\},\ E_2\cup \{z\} \in{\mathcal{F}}$
.
$E_1\cup \{z\},\ E_2\cup \{z\} \in{\mathcal{F}}$
.
Let
![]() $E_0=R_0\cup \{1,x_1\}$
and clearly
$E_0=R_0\cup \{1,x_1\}$
and clearly
![]() $E_0\cap E_2=\emptyset$
. Since
$E_0\cap E_2=\emptyset$
. Since
![]() $E_0\subset G_0\cup \{x_1\}\in{\mathcal{F}}^*$
,
$E_0\subset G_0\cup \{x_1\}\in{\mathcal{F}}^*$
,
![]() $E_0$
is covered by
$E_0$
is covered by
![]() $k$
members of
$k$
members of
![]() $\mathcal{F}$
, we can find
$\mathcal{F}$
, we can find
![]() $w\notin E_2$
such that
$w\notin E_2$
such that
![]() $E_0\cup \{w\}\in{\mathcal{F}}$
. For
$E_0\cup \{w\}\in{\mathcal{F}}$
. For
![]() $k\geq 5$
we may choose
$k\geq 5$
we may choose
![]() $u\in R_1$
,
$u\in R_1$
,
![]() $u\neq w$
. Then
$u\neq w$
. Then
![]() $E_2\cup \{u\}\in{\mathcal{F}}$
and
$E_2\cup \{u\}\in{\mathcal{F}}$
and
![]() $E_0\cup \{w\},\ E_2\cup \{u\}$
are disjoint, a contradiction.
$E_0\cup \{w\},\ E_2\cup \{u\}$
are disjoint, a contradiction.
Claim 11 implies
![]() ${\mathcal{G}}'(H) ={\mathcal{G}}_1^H$
and
${\mathcal{G}}'(H) ={\mathcal{G}}_1^H$
and
![]() $G\cup \{x_1\}\in{\mathcal{F}}^*$
for all
$G\cup \{x_1\}\in{\mathcal{F}}^*$
for all
![]() $G\in{\mathcal{G}}'(H)$
. Then by Lemma 6.1 we may assume that
$G\in{\mathcal{G}}'(H)$
. Then by Lemma 6.1 we may assume that
![]() $\nu ({\mathcal{G}}_1^H([2]))\leq k$
. By (10),
$\nu ({\mathcal{G}}_1^H([2]))\leq k$
. By (10),
contradicting our assumption.
Case 2. For each
![]() $H\in{\mathcal{H}}$
,
$H\in{\mathcal{H}}$
,
![]() $|{\mathcal{G}}'(H)|\leq k(k-1)\binom{n-4}{k-4}$
.
$|{\mathcal{G}}'(H)|\leq k(k-1)\binom{n-4}{k-4}$
.
By the definition of
![]() $\mathcal{E}$
, we infer that each
$\mathcal{E}$
, we infer that each
![]() $E$
in
$E$
in
![]() $\mathcal{E}$
contains a
$\mathcal{E}$
contains a
![]() $(k-1)$
-set
$(k-1)$
-set
![]() $G\in{\mathcal{G}}'$
, implying
$G\in{\mathcal{G}}'$
, implying
![]() $|{\mathcal{E}}|\leq |{\mathcal{G}}'|$
. By Claim 9 and (24),
$|{\mathcal{E}}|\leq |{\mathcal{G}}'|$
. By Claim 9 and (24),
Define
![]() ${\mathcal{F}}_1={\mathcal{F}}^*\setminus{\mathcal{E}}$
. Note that each member of
${\mathcal{F}}_1={\mathcal{F}}^*\setminus{\mathcal{E}}$
. Note that each member of
![]() $\partial{\mathcal{F}}_1$
is a transversal of
$\partial{\mathcal{F}}_1$
is a transversal of
![]() $\mathcal{F}$
. Since
$\mathcal{F}$
. Since
![]() $\mathcal{F}$
is saturated, by Lemma 5.1 (i) the family
$\mathcal{F}$
is saturated, by Lemma 5.1 (i) the family
![]() $\partial{\mathcal{F}}_1$
is intersecting. By Proposition 5.3,
$\partial{\mathcal{F}}_1$
is intersecting. By Proposition 5.3,
![]() ${\mathcal{F}}_1$
is 3-intersecting. If
${\mathcal{F}}_1$
is 3-intersecting. If
![]() $|{\mathcal{F}}_1|\leq k\binom{n-4}{k-4}$
, then
$|{\mathcal{F}}_1|\leq k\binom{n-4}{k-4}$
, then
Otherwise, by (11) we have
![]() $[3]\subset F$
for all
$[3]\subset F$
for all
![]() $F\in{\mathcal{F}}_1$
. Then by Lemma 6.1, we may assume
$F\in{\mathcal{F}}_1$
. Then by Lemma 6.1, we may assume
![]() $\nu ({\mathcal{F}}_1([3]))\leq k$
and (10) implies
$\nu ({\mathcal{F}}_1([3]))\leq k$
and (10) implies
which contradicts the assumption and the proposition is proven.
Let
![]() $g(\nu,\Delta )$
be the maximum number of edges in a graph
$g(\nu,\Delta )$
be the maximum number of edges in a graph
![]() $\mathcal{G}$
with
$\mathcal{G}$
with
![]() $\nu ({\mathcal{G}})\leq \nu$
and the maximum degree at most
$\nu ({\mathcal{G}})\leq \nu$
and the maximum degree at most
![]() $\Delta$
. To determine
$\Delta$
. To determine
![]() $f^*(n,4,4)$
, we need the following result due to Chvátal and Hanson [Reference Chvátal and Hanson2].
$f^*(n,4,4)$
, we need the following result due to Chvátal and Hanson [Reference Chvátal and Hanson2].
Lemma 6.4 ([Reference Chvátal and Hanson2]). For every
![]() $\nu \geq 1$
and
$\nu \geq 1$
and
![]() $\Delta \geq 1$
,
$\Delta \geq 1$
,
Proposition 6.5.
![]() $f^*(n,4,4)=n-3$
for
$f^*(n,4,4)=n-3$
for
![]() $n\geq 63$
.
$n\geq 63$
.
Proof. Let
![]() ${\mathcal{F}}\subset \binom{[n]}{4}$
be a saturated intersecting family. Let
${\mathcal{F}}\subset \binom{[n]}{4}$
be a saturated intersecting family. Let
![]() ${\mathcal{F}}^*$
be the family of
${\mathcal{F}}^*$
be the family of
![]() $4$
-complete sets in
$4$
-complete sets in
![]() $\mathcal{F}$
.
$\mathcal{F}$
.
Claim 12.
If there are
![]() $F_1,F_2\in{\mathcal{F}}^*$
with
$F_1,F_2\in{\mathcal{F}}^*$
with
![]() $|F_1\cap F_2|=1$
, then
$|F_1\cap F_2|=1$
, then
![]() $|{\mathcal{F}}^*|\leq 35$
.
$|{\mathcal{F}}^*|\leq 35$
.
Proof. Without loss of generality, assume that
![]() $F_1=(x_1,x_2,x_3,z)$
and
$F_1=(x_1,x_2,x_3,z)$
and
![]() $F_2=(y_1,y_2,y_3,z)$
. Using that
$F_2=(y_1,y_2,y_3,z)$
. Using that
![]() $(x_1,x_2,x_3)$
is 4-fold covered in
$(x_1,x_2,x_3)$
is 4-fold covered in
![]() $\mathcal{F}$
which is intersecting, the only possible extra 4-sets are
$\mathcal{F}$
which is intersecting, the only possible extra 4-sets are
![]() $(x_1,x_2,x_3,y_i)\in{\mathcal{F}}$
,
$(x_1,x_2,x_3,y_i)\in{\mathcal{F}}$
,
![]() $1\leq i\leq 3$
. Similarly for
$1\leq i\leq 3$
. Similarly for
![]() $(y_1,y_2,y_3)$
we infer
$(y_1,y_2,y_3)$
we infer
![]() $(y_1,y_2,y_3,x_j)\in{\mathcal{F}}$
,
$(y_1,y_2,y_3,x_j)\in{\mathcal{F}}$
,
![]() $1\leq j\leq 3$
. Now consider
$1\leq j\leq 3$
. Now consider
![]() $(x_1,x_2,z)$
, it is disjoint to
$(x_1,x_2,z)$
, it is disjoint to
![]() $(y_1,y_2,y_3,x_3)$
. Hence its covering sets are
$(y_1,y_2,y_3,x_3)$
. Hence its covering sets are
![]() $(x_1,x_2,x_3,z)$
and
$(x_1,x_2,x_3,z)$
and
![]() $(x_1,x_2,z,y_i)\in{\mathcal{F}}$
,
$(x_1,x_2,z,y_i)\in{\mathcal{F}}$
,
![]() $1\leq i\leq 3$
. Arguing in the same way with
$1\leq i\leq 3$
. Arguing in the same way with
![]() $(x_1,x_3,z),(x_2,x_3,z),(y_1,y_2,z)$
, etc, we infer that all sets
$(x_1,x_3,z),(x_2,x_3,z),(y_1,y_2,z)$
, etc, we infer that all sets
![]() $R\in \binom{F_1\cup F_2}{4}$
with
$R\in \binom{F_1\cup F_2}{4}$
with
![]() $z\in R$
are in
$z\in R$
are in
![]() $\mathcal{F}$
. If
$\mathcal{F}$
. If
![]() ${\mathcal{F}}\subset \binom{F_1\cup F_2}{4}$
then
${\mathcal{F}}\subset \binom{F_1\cup F_2}{4}$
then
![]() $|{\mathcal{F}}^*|\leq |{\mathcal{F}}|\leq \binom{7}{4}=35$
, we are done. Otherwise we infer
$|{\mathcal{F}}^*|\leq |{\mathcal{F}}|\leq \binom{7}{4}=35$
, we are done. Otherwise we infer
![]() $z\in F$
for all
$z\in F$
for all
![]() $F\in{\mathcal{F}}\setminus \binom{F_1\cup F_2}{4}$
. Using
$F\in{\mathcal{F}}\setminus \binom{F_1\cup F_2}{4}$
. Using
![]() $F\cap (x_1,x_2,x_3,y_i)\neq \emptyset$
and
$F\cap (x_1,x_2,x_3,y_i)\neq \emptyset$
and
![]() $F\cap (y_1,y_2,y_3,x_j)\neq \emptyset$
, we infer that such
$F\cap (y_1,y_2,y_3,x_j)\neq \emptyset$
, we infer that such
![]() $F$
are of form
$F$
are of form
![]() $(x_j,y_i,z,w_t)$
with
$(x_j,y_i,z,w_t)$
with
![]() $w_t$
in the outside of
$w_t$
in the outside of
![]() $F_1\cup F_2$
. Now the intersecting property implies that
$F_1\cup F_2$
. Now the intersecting property implies that
![]() $(x_j,y_i,w_t)$
cannot be 4-fold covered by
$(x_j,y_i,w_t)$
cannot be 4-fold covered by
![]() $\mathcal{F}$
. Thus
$\mathcal{F}$
. Thus
![]() $(x_j,y_i,z,w_t)\notin{\mathcal{F}}^*$
. Hence
$(x_j,y_i,z,w_t)\notin{\mathcal{F}}^*$
. Hence
![]() $|{\mathcal{F}}^*|\leq \binom{7}{4}=35$
.
$|{\mathcal{F}}^*|\leq \binom{7}{4}=35$
.
By Claim 12 and
![]() $n\geq 38$
, we may assume that
$n\geq 38$
, we may assume that
![]() ${\mathcal{F}}^*$
is 2-intersecting.
${\mathcal{F}}^*$
is 2-intersecting.
Claim 13.
![]() ${\mathcal{F}}^*$
contains no sunflower with 3 petals and a centre of size 2.
${\mathcal{F}}^*$
contains no sunflower with 3 petals and a centre of size 2.
Proof. Assume that
![]() $(1,2,3,4), (1,2,5,6),(1,2,7,8)$
form such a sunflower in
$(1,2,3,4), (1,2,5,6),(1,2,7,8)$
form such a sunflower in
![]() ${\mathcal{F}}^*$
. Since
${\mathcal{F}}^*$
. Since
![]() $(2,3,4),(1,5,6)$
are 4-fold covered in
$(2,3,4),(1,5,6)$
are 4-fold covered in
![]() $\mathcal{F}$
, we may assume that
$\mathcal{F}$
, we may assume that
The intersecting property of
![]() $\mathcal{F}$
implies that (by symmetry)
$\mathcal{F}$
implies that (by symmetry)
![]() $(a,b)=(5,6)$
,
$(a,b)=(5,6)$
,
![]() $(p,q)=(3,4)$
,
$(p,q)=(3,4)$
,
![]() $c=r$
. Since
$c=r$
. Since
![]() $(1,7,8)$
is 4-fold covered in
$(1,7,8)$
is 4-fold covered in
![]() $\mathcal{F}$
, let
$\mathcal{F}$
, let
![]() $(1,7,8,u),(1,7,8,v),(1,7,8,w)\in{\mathcal{F}}$
. Then one of
$(1,7,8,u),(1,7,8,v),(1,7,8,w)\in{\mathcal{F}}$
. Then one of
![]() $u,v,w$
is not in
$u,v,w$
is not in
![]() $\{5,6\}$
, by symmetry assume
$\{5,6\}$
, by symmetry assume
![]() $w\notin \{5,6\}$
, it implies that
$w\notin \{5,6\}$
, it implies that
![]() $(2,3,4,a),(1,7,8,w)$
are disjoint, a contradiction.
$(2,3,4,a),(1,7,8,w)$
are disjoint, a contradiction.
Let
![]() $F\in{\mathcal{F}}^*$
. For any
$F\in{\mathcal{F}}^*$
. For any
![]() $P\in \binom{F}{2}$
, define
$P\in \binom{F}{2}$
, define
By Claim 13,
![]() $\nu ({\mathcal{G}}(P))\leq 2$
. By Lemma 6.1, we may assume that
$\nu ({\mathcal{G}}(P))\leq 2$
. By Lemma 6.1, we may assume that
![]() ${\mathcal{F}}^*$
contains no sunflower with
${\mathcal{F}}^*$
contains no sunflower with
![]() $5$
petals and a centre of size
$5$
petals and a centre of size
![]() $3$
. It follows that the maximum degree of
$3$
. It follows that the maximum degree of
![]() ${\mathcal{G}}(P)$
is at most 4. Then (25) implies
${\mathcal{G}}(P)$
is at most 4. Then (25) implies
![]() $|{\mathcal{G}}(P)|\leq 2*4+2=10$
. Since
$|{\mathcal{G}}(P)|\leq 2*4+2=10$
. Since
![]() ${\mathcal{F}}^*$
is 2-intersecting, we conclude that for
${\mathcal{F}}^*$
is 2-intersecting, we conclude that for
![]() $n\geq 63$
,
$n\geq 63$
,
 \begin{equation*} |{\mathcal {F}}^*| \leq \sum _{P\in \binom {F}{2}} |{\mathcal {G}}(P)| \leq \binom {4}{2} *10 =60\leq n-3 \end{equation*}
\begin{equation*} |{\mathcal {F}}^*| \leq \sum _{P\in \binom {F}{2}} |{\mathcal {G}}(P)| \leq \binom {4}{2} *10 =60\leq n-3 \end{equation*}
and the proposition is proven.
Theorem 1.8 follows from Theorem 3.1 and Propositions 5.4, 5.5, 6.2, 6.3, 6.5.
7. Concluding remarks
In this paper we considered intersecting
![]() $k$
-graphs
$k$
-graphs
![]() ${\mathcal{F}}\subset \binom{[n]}{k}$
. For a positive parameter
${\mathcal{F}}\subset \binom{[n]}{k}$
. For a positive parameter
![]() $r$
we called an edge
$r$
we called an edge
![]() $F\in{\mathcal{F}}$
$F\in{\mathcal{F}}$
![]() $r$
-complete if all
$r$
-complete if all
![]() $G\in \binom{F}{k-1}$
were contained in at least
$G\in \binom{F}{k-1}$
were contained in at least
![]() $r$
members of
$r$
members of
![]() $\mathcal{F}$
, including
$\mathcal{F}$
, including
![]() $F$
. For
$F$
. For
![]() $r=1$
this condition is automatically satisfied. For
$r=1$
this condition is automatically satisfied. For
![]() $r\geq 2$
we defined
$r\geq 2$
we defined
![]() $f(n,k,r)$
as the maximum of
$f(n,k,r)$
as the maximum of
![]() $|{\mathcal{F}}|$
for families with all edges being
$|{\mathcal{F}}|$
for families with all edges being
![]() $r$
-complete and
$r$
-complete and
![]() $f^*(n,k,r)$
as the maximum number of
$f^*(n,k,r)$
as the maximum number of
![]() $r$
-complete edges in
$r$
-complete edges in
![]() $\mathcal{F}$
. The inequality
$\mathcal{F}$
. The inequality
![]() $f(n,k,r)\leq f^*(n,k,r)$
is obvious. For
$f(n,k,r)\leq f^*(n,k,r)$
is obvious. For
![]() $2\leq r\leq k$
all edges of the family
$2\leq r\leq k$
all edges of the family
are
![]() $r$
-complete. We showed that for
$r$
-complete. We showed that for
![]() $n\geq n_0(k,r)$
,
$n\geq n_0(k,r)$
,
![]() $f(n,k,r)=|{\mathcal{L}}(n,k,r)|$
and for
$f(n,k,r)=|{\mathcal{L}}(n,k,r)|$
and for
![]() $r=2$
or 3 even
$r=2$
or 3 even
![]() $f^*(n,k,r)$
shares this value. However, for
$f^*(n,k,r)$
shares this value. However, for
![]() $r\geq 4$
,
$r\geq 4$
,
![]() $f^*(n,k,r)$
is much larger:
$f^*(n,k,r)$
is much larger:
In the case
![]() $r=2$
we exploited some connections with the Erdős Matching Conjecture and succeeded in proving the statements with a linear constraint,
$r=2$
we exploited some connections with the Erdős Matching Conjecture and succeeded in proving the statements with a linear constraint,
![]() $n\geq 28k$
. However for
$n\geq 28k$
. However for
![]() $r\geq 3$
our proof requires
$r\geq 3$
our proof requires
![]() $n_0(k,r)\gt k^{2(r+1)k}$
.
$n_0(k,r)\gt k^{2(r+1)k}$
.
Problem 7.1.
Does
![]() $f(n,k,r)=|{\mathcal{L}}(n,k,r)|$
hold for
$f(n,k,r)=|{\mathcal{L}}(n,k,r)|$
hold for
![]() $3\leq r\leq k$
and
$3\leq r\leq k$
and
![]() $n\gt ck$
with an absolute constant
$n\gt ck$
with an absolute constant
![]() $c$
?
$c$
?
Another open problem is to determine the exact value of
![]() $f^*(n,k,r)$
for
$f^*(n,k,r)$
for
![]() $4\leq r\leq k-1$
and
$4\leq r\leq k-1$
and
![]() $n\gt n_0(k,r)$
.
$n\gt n_0(k,r)$
.
As the analogous problems for
![]() $t$
-intersecting families, we can define two more functions.
$t$
-intersecting families, we can define two more functions.
 \begin{align*} &f(n,k,t,r)=\max \left \{|{\mathcal{F}}|\colon{\mathcal{F}}\subset \binom{[n]}{k} \text{ is}\ t\text{-intersecting and } r\text{-complete}\right \},\\ &f^*(n,k,t,r)=\max \left \{|{\mathcal{F}}^*|\colon \begin{array}{l@{\quad}l} \exists{\mathcal{F}}\subset \binom{[n]}{k} \text{ is } t\text{-intersecting},\ {\mathcal{F}}^*\subset{\mathcal{F}}, \\[3pt]{\mathcal{F}}^* \text{ is relatively }r\text{-complete in }{\mathcal{F}} \end{array}\right \}. \end{align*}
\begin{align*} &f(n,k,t,r)=\max \left \{|{\mathcal{F}}|\colon{\mathcal{F}}\subset \binom{[n]}{k} \text{ is}\ t\text{-intersecting and } r\text{-complete}\right \},\\ &f^*(n,k,t,r)=\max \left \{|{\mathcal{F}}^*|\colon \begin{array}{l@{\quad}l} \exists{\mathcal{F}}\subset \binom{[n]}{k} \text{ is } t\text{-intersecting},\ {\mathcal{F}}^*\subset{\mathcal{F}}, \\[3pt]{\mathcal{F}}^* \text{ is relatively }r\text{-complete in }{\mathcal{F}} \end{array}\right \}. \end{align*}
Example 7.2. For
![]() $n\geq k\geq t\geq 1$
and
$n\geq k\geq t\geq 1$
and
![]() $1\leq r\leq k-t+1$
define
$1\leq r\leq k-t+1$
define
By essentially the same proof as in Sections 3 and 4, one can obtain the following two results:
Theorem 7.3.
For
![]() $k\geq 3$
,
$k\geq 3$
,
![]() $r\geq 2$
and
$r\geq 2$
and
![]() $n\geq n_0(k,r)$
,
$n\geq n_0(k,r)$
,
 \begin{align} f(n,k,t,r) = \left \{\begin{array}{l@{\quad}l} |{\mathcal{A}}(n,k,t,r)|,& 2\leq r\leq k-t+1;\\[5pt] 0. &r\geq k-t+2. \end{array}\right . \end{align}
\begin{align} f(n,k,t,r) = \left \{\begin{array}{l@{\quad}l} |{\mathcal{A}}(n,k,t,r)|,& 2\leq r\leq k-t+1;\\[5pt] 0. &r\geq k-t+2. \end{array}\right . \end{align}
Theorem 7.4.
For
![]() $k\geq 3$
,
$k\geq 3$
,
![]() $r\geq 2$
and
$r\geq 2$
and
![]() $n\geq n_0(k,r)$
,
$n\geq n_0(k,r)$
,
 \begin{align} f^*(n,k,t,r) = \left \{\begin{array}{l@{\quad}l} |{\mathcal{A}}(n,k,t,r)|,&r=2,3;\\[5pt] \binom{n-t-2}{k-t-2}+O(n^{k-t-r+1}), &4\leq r\leq k-t+1;\\[5pt] \binom{n-t-2}{k-t-2},& r\geq k-t+2. \end{array}\right . \end{align}
\begin{align} f^*(n,k,t,r) = \left \{\begin{array}{l@{\quad}l} |{\mathcal{A}}(n,k,t,r)|,&r=2,3;\\[5pt] \binom{n-t-2}{k-t-2}+O(n^{k-t-r+1}), &4\leq r\leq k-t+1;\\[5pt] \binom{n-t-2}{k-t-2},& r\geq k-t+2. \end{array}\right . \end{align}
Acknowledgement
We would like to thank the referees for their helpful comments and corrections.