Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Yuster, Raphael
2017.
On the longest path of a randomly weighted tournament.
Discrete Applied Mathematics,
Vol. 230,
Issue. ,
p.
121.
Frieze, Alan
and
Johansson, Tony
2017.
Minimum Cost Matching in a Random Graph with Random Costs.
SIAM Journal on Discrete Mathematics,
Vol. 31,
Issue. 1,
p.
489.
Hiraoka, Yasuaki
and
Shirai, Tomoyuki
2017.
Minimum spanning acycle and lifetime of persistent homology in the Linial-Meshulam process.
Random Structures & Algorithms,
Vol. 51,
Issue. 2,
p.
315.
Sen, Subhabrata
2018.
Optimization on sparse random hypergraphs and spin glasses.
Random Structures & Algorithms,
Vol. 53,
Issue. 3,
p.
504.
FRIEZE, ALAN
and
JOHANSSON, TONY
2018.
On Edge-Disjoint Spanning Trees in a Randomly Weighted Complete Graph.
Combinatorics, Probability and Computing,
Vol. 27,
Issue. 2,
p.
228.
Gimadi, Edward
Shevyakov, Alexandr
and
Shin, Ekaterina
2019.
Asymptotically Optimal Approach to a Given Diameter Undirected MST Problem on Random Input Data.
p.
48.
Gimadi, Edward Kh.
and
Shin, Ekaterina Yu.
2019.
Mathematical Optimization Theory and Operations Research.
Vol. 1090,
Issue. ,
p.
30.
Gimadi, Edward K.
Shevyakov, Aleksandr S.
and
Shtepa, Alexandr A.
2020.
Optimization and Applications.
Vol. 12422,
Issue. ,
p.
110.
Kovchegov, Yevgeniy
Otto, Peter T.
and
Yambartsev, Anatoly
2021.
Cross-multiplicative coalescent processes and applications
.
Latin American Journal of Probability and Mathematical Statistics,
Vol. 18,
Issue. 1,
p.
81.
Gimadi, Edward Kh.
Shevyakov, Aleksandr S.
and
Shtepa, Alexandr A.
2021.
Mathematical Optimization Theory and Operations Research.
Vol. 12755,
Issue. ,
p.
67.
Janson, Svante
and
Sorkin, Gregory B.
2022.
Successive minimum spanning trees.
Random Structures & Algorithms,
Vol. 61,
Issue. 1,
p.
126.
Silwal, Sandeep
2022.
A concentration inequality for the facility location problem.
Operations Research Letters,
Vol. 50,
Issue. 2,
p.
213.
Gimadi, Eduard Kh.
Shevyakov, Aleksandr S.
and
Shtepa, Aleksandr A.
2022.
Recent Trends in Analysis of Images, Social Networks and Texts.
Vol. 1573,
Issue. ,
p.
195.
Gimadi, E. Kh.
and
Shtepa, A. A.
2023.
On Asymptotically Optimal Approach for Finding of the Minimum Total Weight of Edge-Disjoint Spanning Trees with a Given Diameter.
Automation and Remote Control,
Vol. 84,
Issue. 7,
p.
772.
Fredes, Luis
and
Marckert, Jean-François
2023.
Models of random subtrees of a graph.
Probability Surveys,
Vol. 20,
Issue. none,
Kovchegov, Yevgeniy
and
Otto, Peter T.
2023.
Multidimensional Lambert–Euler inversion and Vector-Multiplicative Coalescent Processes.
Journal of Statistical Physics,
Vol. 190,
Issue. 12,
Gimadi, E. Kh.
and
Shtepa, A. A.
2024.
Analysis of Images, Social Networks and Texts.
Vol. 14486,
Issue. ,
p.
341.
Gimadi, E. Kh.
2024.
Advances in Optimization and Applications.
Vol. 1913,
Issue. ,
p.
281.
 $\mathbb{E}$(Ln) = ζ(3) and show that
$\mathbb{E}$(Ln) = ζ(3) and show that
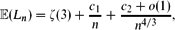 $$
\mathbb{E}(L_n)=\zeta(3)+\frac{c_1}{n}+\frac{c_2+o(1)}{n^{4/3}},
$$
$$
\mathbb{E}(L_n)=\zeta(3)+\frac{c_1}{n}+\frac{c_2+o(1)}{n^{4/3}},
$$



