No CrossRef data available.
Article contents
Adding Edges to Increase the Chromatic Number of a Graph
Published online by Cambridge University Press: 31 March 2016
Abstract
If n ⩾ k + 1 and G is a connected n-vertex graph, then one can add 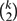 $\binom{k}{2}$ edges to G so that the resulting graph contains the complete graph Kk+1. This yields that for any connected graph G with at least k + 1 vertices, one can add
$\binom{k}{2}$ edges to G so that the resulting graph contains the complete graph Kk+1. This yields that for any connected graph G with at least k + 1 vertices, one can add 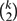 $\binom{k}{2}$ edges to G so that the resulting graph has chromatic number > k. A long time ago, Bollobás suggested that for every k ⩾ 3 there exists a k-chromatic graph Gk such that after adding to it any
$\binom{k}{2}$ edges to G so that the resulting graph has chromatic number > k. A long time ago, Bollobás suggested that for every k ⩾ 3 there exists a k-chromatic graph Gk such that after adding to it any 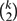 $\binom{k}{2}$ − 1 edges, the chromatic number of the resulting graph is still k. In this note we prove this conjecture.
$\binom{k}{2}$ − 1 edges, the chromatic number of the resulting graph is still k. In this note we prove this conjecture.
MSC classification
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2016




