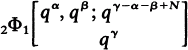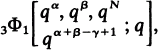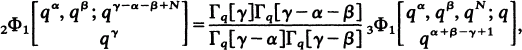Research Article
Some Pointwise Convergence Results in Lp(μ), 1 < p < ∞
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 277-284
-
- Article
-
- You have access
- Export citation
Dilations of Positive Contractions on Lp Spaces*
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 285-292
-
- Article
-
- You have access
- Export citation
On the Duals of Flat Banach Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 293-299
-
- Article
-
- You have access
- Export citation
On an Arithmetic Convolution
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 301-305
-
- Article
-
- You have access
- Export citation
On Some Integral Inequalities Related to Hardy's
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 307-312
-
- Article
-
- You have access
- Export citation
Dimension Theory Via Bisector Chains
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 313-317
-
- Article
-
- You have access
- Export citation
The Spectrum of a Finite Lattice: Breadth and Length Techniques
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 319-329
-
- Article
-
- You have access
- Export citation
Abelian Theorems for Hardy Transformations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 331-335
-
- Article
-
- You have access
- Export citation
Some Results in the Theory of Fibrations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 337-345
-
- Article
-
- You have access
- Export citation
Orthogonally Complete Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 347-351
-
- Article
-
- You have access
- Export citation
A Characterization of the Lebesgue Integral
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 353-357
-
- Article
-
- You have access
- Export citation
Infinite Geometric Products
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 359-367
-
- Article
-
- You have access
- Export citation
Certain Summation Formulae for Basic Hypergeometric Series
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 369-375
-
- Article
-
- You have access
- Export citation
Variants of the Hölder Inequality and its Inverses
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 377-384
-
- Article
-
- You have access
- Export citation
Instabilité Des Corps Formellement Réels
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 385-387
-
- Article
-
- You have access
- Export citation
Applications of Decomposition Theorems to Trivializing h-Cobordisms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 389-391
-
- Article
-
- You have access
- Export citation
Extensions of Orderable Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 393-395
-
- Article
-
- You have access
- Export citation
On the Order of the Error Function of the (k, r)-Integers—II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 397-399
-
- Article
-
- You have access
- Export citation
Trivectors in a Space of Seven Dimensions
-
- Published online by Cambridge University Press:
- 20 November 2018, p. 401
-
- Article
-
- You have access
- Export citation



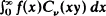 and
and 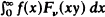 of a suitably chosen function
of a suitably chosen function 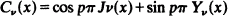
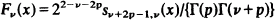
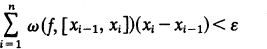
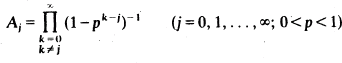
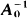 is tabulated for
is tabulated for