Hostname: page-component-848d4c4894-xm8r8 Total loading time: 0 Render date: 2024-06-22T14:35:01.079Z Has data issue: false hasContentIssue false
  • English
  • Français

Weighted Mean Operators on lp

Published online by Cambridge University Press:  20 November 2018

David Borwein
David Borwein*
Affiliation:
Department of Mathematics, University of Western Ontario, London, Ontario, N6A 5B7, email: dborwein@uwo.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Abstract. The weighted mean matrix 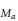${{M}_{a}}$ is the triangular matrix 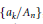$\left\{ {{a}_{k}}/{{A}_{n}} \right\}$, where 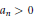${{a}_{n}}\,>\,0$ and 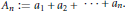${{A}_{n}}\,:=\,{{a}_{1}}\,+\,{{a}_{2}}\,+\cdots +\,{{a}_{n}}$. It is proved that, subject to 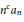${{n}^{c}}{{a}_{n}}$ being eventually monotonic for each constant 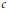$c$ and to the existence of 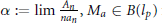$\alpha \,:=\,\lim \,\frac{{{A}_{n}}}{n{{a}_{n}}},\,{{M}_{a}}\,\in \,B\left( {{l}_{p}} \right)$ for 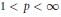$1\,<\,p\,<\infty $ if and only if 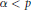$\alpha \,<\,p$.

Keywords

47B3747A3040G05weighted meansoperators on lpnorm estimates
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 43 , Issue 4 , 01 December 2000 , pp. 406 - 412
Copyright
Copyright © Canadian Mathematical Society 2000

References

[1] Bennett, G., Some elementary inequalities. Quart. J. Math. Oxford (2) 38 (1987), 401–425.Google Scholar
[2] Borwein, D. and Jakimovski, A., Matrix operators on lp. Rocky Mountain J. Math. 9 (1979), 463–477.Google Scholar
[3] Borwein, D., Simple conditions for matrices as bounded operators on lp. Canad. Math. Bull. 41 (1998), 10–14.Google Scholar
[4] Borwein, D., Generalized Hausdorff matrices as bounded operators on lp. Math. Z. 83 (1983), 483–487.Google Scholar
[5] Cartlidge, J. M. Weighted mean matrices as operators on lp. Ph.D. thesis, Indiana University, 1978.Google Scholar
[6] Cass, F. P. and Kratz, W., Nörlund and weighted mean matrices as bounded operators on lp. Rocky Mountain J. Math. 20 (1990), 59–74.Google Scholar
[7] Hardy, G. H., Orders of Infinity. Cambridge, 1954.Google Scholar