Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-25T14:06:56.726Z Has data issue: false hasContentIssue false
  • English
  • Français

Weak Sequential Completeness of 𝑲(X,Y)

Published online by Cambridge University Press:  20 November 2018

Qingying Bu
Qingying Bu*
Affiliation:
Department of Mathematics, University of Mississippi, University, MS 38677, USA e-mail: qbu@olemiss.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

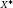For Banach spaces $X$ and $Y$, we show that if ${{X}^{*}}$ and $Y$ are weakly sequentially complete and every weakly compact operator from $X$ to $Y$ is compact, then the space of all compact operators from $X$ to $Y$ is weakly sequentially complete. The converse is also true if, in addition, either 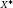${{X}^{*}}$ or $Y$ has the bounded compact approximation property.

Keywords

46B2546B28weak sequential completenessreflexivitycompact operator space
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 3 , 01 September 2013 , pp. 503 - 509
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Amir, D. and Lindenstrauss, J., The structure of weakly compact sets in Banach spaces. Ann. of Math. 88 (1968), 35–46. http://dx.doi.org/10.2307/1970554 Google Scholar
[2] Astala, K. and Tylli, H.-O., On the bounded compact approximation property and measures of noncompactness. J. Funct. Anal. 70 (1987), no. 2, 388–401. http://dx.doi.org/10.1016/0022-1236(8790118-2 Google Scholar
[3] Baker, J. M., Reflexivity of operator spaces. Proc. Amer. Math. Soc. 85 (1982), no. 3, 366–368. http://dx.doi.org/10.1090/S0002-9939-1982-0656104-0 Google Scholar
[4] Casazza, P. G. and Shura, T. J., Tsirel’son’s space. Lecture Notes in Mathematics, 1363, Springer-Verlag, Berlin, 1989.Google Scholar
[5] Feder, M. and Saphar, P. D., Spaces of compact operators and their dual spaces. Israel J. Math. 21 (1975), no. 1, 38–49. http://dx.doi.org/10.1007/BF02757132 Google Scholar
[6] Godefroy, G. and Saphar, P. D., Duality in spaces of operators and smooth norms on Banach spaces. Illinois J. Math. 32 (1988), no. 4, 672–695.Google Scholar
[7] González, M. and Gutiérrez, J. M., Polynomial Grothendieck properties. Glasgow Math. J. 37 (1995), no. 2, 211–219. http://dx.doi.org/10.1017/S0017089500031116 Google Scholar
[8] Holub, J. R., Reflexivity of L(E; F). Proc. Amer. Math. Soc. 39 (1973), 175–177.Google Scholar
[9] Kalton, N. J., Spaces of compact operators. Math. Ann. 208 (1974), 267–278. http://dx.doi.org/10.1007/BF01432152 Google Scholar
[10] Lewis, D. R., Conditional weak compactness in certain inductive tensor products. Math. Ann. 201 (1973), 201–209. http://dx.doi.org/10.1007/BF01427942 Google Scholar
[11] Megginson, R. E., An introduction to Banach space theory. Graduate Texts in Mathematics, 183, Springer-Verlag, New York, 1998.Google Scholar
[12] Pisier, G., Factorization of linear operators and geometry of Banach spaces. CBMS Regional Conference Series in Mathematics, 60, Published for the Conference Board of the Mathematical Sciences,Washington, DC; by the American Mathematical Society, Providence, RI, 1986.Google Scholar
[13] Rosenthal, H. P., On quasi-complemented subspaces of Banach spaces, with an appendix on compactness of operators from Lp to Lr. J. Functional Anal. 4 (1969), 176–214. http://dx.doi.org/10.1016/0022-1236(6990011-1) Google Scholar
[14] Ruckle, W., Reflexivity of L(E; F). Proc. Amer. Math. Soc. 34 (1972), 171–174.Google Scholar
[15] Schatten, R., The space of completely continuous operators on a Hilbert space. Math. Ann. 134 (1957), 47–49. http://dx.doi.org/10.1007/BF01342831 Google Scholar
[16] Wilansky, A., Modern methods in topological vector spaces. McGraw-Hill, New York, 1978).Google Scholar
[17] Willis, G., The compact approximation property does not imply the approximation property. Studia Math. 103 (1992), no. 1, 99–108.Google Scholar