Hostname: page-component-848d4c4894-8bljj Total loading time: 0 Render date: 2024-06-30T02:43:49.657Z Has data issue: false hasContentIssue false
  • English
  • Français

Universal Singular Inner Functions

Published online by Cambridge University Press:  20 November 2018

Pamela Gorkin  and
Raymond Mortini
Pamela Gorkin
Affiliation:
Department of Mathematics Bucknell University Lewisburg, Pennsylvania 17837 USA, e-mail: pgorkin@bucknell.edu
Raymond Mortini
Affiliation:
Département de Mathématiques Université de Metz Ile du Saulcy F-57045 Metz France, e-mail: mortini@poncelet.univ-metz.fr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that there exists a singular inner function $S$ which is universal for noneuclidean translates; that is one for which the set 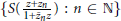$\{S(\frac{z\,+\,{{z}_{n}}}{1\,+\,{{{\bar{z}}}_{n}}z})\,:\,n\,\in \,\mathbb{N}\}$ is locally uniformly dense in the set of all zero-free holomorphic functions in 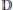$\mathbb{D}$ bounded by one.

Keywords

30D50
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 47 , Issue 1 , 01 March 2004 , pp. 17 - 21
Copyright
Copyright © Canadian Mathematical Society 2004

References

[De] Decker, E., On the boundary behaviour of singular inner functions. Michigan Math. J. 41 (1994), 547–562.Google Scholar
[Ga] Garnett, J. B., Bounded Analytic Functions. Academic Press, New York, 1981.Google Scholar
[GM] Gorkin, P. and Mortini, R., Asymptotic interpolating sequences in uniform algebras. J. London Math. Soc. 67 (2003), 481–498.Google Scholar
[GE] Grosse-Erdmann, K.-G., Universal families and hypercyclic operators. Bull. Amer. Math. Soc. 36 (1999), 345–381.Google Scholar
[GI] Guillory, C. and Izuchi, K., Interpolating Blaschke products of type G. Complex Variables Theory Appl. 31 (1996), 51–64.Google Scholar
[H] Hedenmalm, H., Thin interpolating sequences and three algebras of bounded functions. Proc. Amer. Math. Soc. 99 (1987), 489–495.Google Scholar
[He] Heins, M., A universal Blaschke product. Arch. Math. 6 (1955), 41–44.Google Scholar
[Ho] Hoffman, K., Banach Spaces of Analytic Functions. Dover Publ., New York 1988, reprint of 1962.Google Scholar