Hostname: page-component-76fb5796d-zzh7m Total loading time: 0 Render date: 2024-04-26T16:05:49.647Z Has data issue: false hasContentIssue false
  • English
  • Français

Trivial Units for Group Rings with G-adapted Coefficient Rings

Published online by Cambridge University Press:  20 November 2018

Allen Herman ,
Yuanlin Li  and
M. M. Parmenter
Allen Herman
Affiliation:
Department of Mathematics and Statistics, University of Regina, Regina, SK, S4S 0A2 e-mail: aherman@math.uregina.ca
Yuanlin Li
Affiliation:
Department of Mathematics, Brock University, St. Catharines, ON, L2S 3A1 e-mail: Yuanlin.Li@brocku.ca
M. M. Parmenter
Affiliation:
Department of Mathematics and Statistics, Memorial University of Newfoundland, St. John's, NF, A1C 5S7 e-mail: michael1@math.mun.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For each finite group 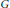$G$ for which the integral group ring 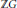$\mathbb{Z}G$ has only trivial units, we give ring-theoretic conditions for a commutative ring 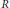$R$ under which the group ring 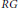$RG$ has nontrivial units. Several examples of rings satisfying the conditions and rings not satisfying the conditions are given. In addition, we extend a well-known result for fields by showing that if 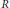$R$ is a ring of finite characteristic and 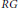$RG$ has only trivial units, then 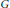$G$ has order at most 3.

Keywords

16S3416U6020C05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 48 , Issue 1 , 01 March 2005 , pp. 80 - 89
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Bovdi, A., The group of units of a group algebra of characteristic p. Publ. Math. Debrecen. 52(1998), 193–244.Google Scholar
[2] Coleman, D. B. and Enochs, E. E., Isomorphic polynomial rings. Proc. Amer.Math. Soc. 27(1971) 247–252.Google Scholar
[3] Higman, G., The units of group-rings. Proc. LondonMath. Soc. 46(1940), 231–248.Google Scholar
[4] Jespers, E., Parmenter, M., and Smith, P. F., Revisiting a theorem of Higman. LondonMath. Soc. Lecture Note Ser., 211, Cambridge University Press, Cambridge, 1995, pp. 269–273.Google Scholar
[5] Li, Yuanlin, The normalizer of a metabelian group in its integral group ring. J. Algebr. 256(2002), 343–351.Google Scholar
[6] Passman, D. S., The Algebraic Structure of Group Rings. Wiley-Interscience, New York, 1977.Google Scholar
[7] Milies, César Polcino and Sehgal, Sudarshan K., An Introduction to Group Rings. Kluwer, 2002.Google Scholar
[8] Strojnowski, A., A note on u.p. groups. Comm. Algebr. 3(1980), 231–234.Google Scholar