Hostname: page-component-84b7d79bbc-c654p Total loading time: 0 Render date: 2024-07-29T07:56:04.374Z Has data issue: false hasContentIssue false
  • English
  • Français

Steepest Descent and Least Squares Solvability

Published online by Cambridge University Press:  20 November 2018

C. W. Groetsch
C. W. Groetsch*
Affiliation:
University of Cincinnati Cincinnati, Ohio 45221
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let T be a bounded linear operator defined on a Hilbert space H. An element z∈H is called a least squares solution of the equation

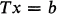
if 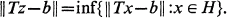. It is easily shown that z is a least squares solution of (1) if and only if z satisfies the normal equation

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 17 , Issue 2 , 01 June 1974 , pp. 275 - 276
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Browder, F. E. and Petryshyn, W. V., The solution by iteration of nonlinear functional equations in Banach spaces, Bull. Amer. Math. Soc. 72 (1966), 571-575.Google Scholar
2. Diaz, J. B. and Metcalf, F. T., On iterative procedures for equations of the first kind, Ax=y, and Picard’s criterion for the existence of a solution, Math. Comp. 24 (1970), 923-935.Google Scholar
3. Kammerer, W. J. and Nashed, M. Z., Steepest descent for singular linear operators with nonclosed range, Appl. Anal. 1 (1971), 143-159.Google Scholar
4. Kammerer, W. J. and Nashed, M. Z., Iterative methods for best approximate solutions of linear integral equations of the first and second kind, MRC Technical Summary Report #1117, Mathematics Research Center, University of Wisconsin, 1971.Google Scholar
5. Nashed, M. Z., Steepest descent for singular linear operator equations, SIAM J.Number. Anal. 7 (1970), 358-362.Google Scholar
6. Nashed, M. Z. and Wahba, Grace, Convergence rates of approximate least squares solutions of linear integral and operator equations of the first kind, MRC Technical Summary Report #1260, Mathematics Research Center, University of Wisconsin, 1972.Google Scholar
7. Smithies, F., Integral Equations, Cambridge University Press, New York, 1970.Google Scholar