Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-24T09:00:06.188Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectrality of a class of Moran measures on 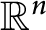$\mathbb {R}^{n}$ with consecutive digit sets

Part of: Nontrigonometric harmonic analysis Normed linear spaces and Banach spaces; Banach lattices Classical measure theory

Published online by Cambridge University Press:  13 April 2022

Si Chen  and
Qian Li
Si Chen
Affiliation:
College of Mathematics and Computational Science, Hunan First Normal University, Changsha 410205, China e-mail: csjl0432@163.com
Qian Li*
Affiliation:
School of Mathematics and Statistics, Central China Normal University, Wuhan 430079, China
*
e-mail: liqian303606@163.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 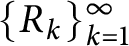$\{R_{k}\}_{k=1}^{\infty }$ be a sequence of expanding integer matrices in 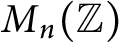$M_{n}(\mathbb {Z})$ , and let 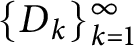$\{D_{k}\}_{k=1}^{\infty }$ be a sequence of finite digit sets with integer vectors in 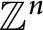${\mathbb Z}^{n}$ . In this paper, we prove that under certain conditions in terms of 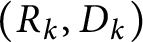$(R_{k},D_{k})$ for 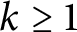$k\ge 1$ , the Moran measure

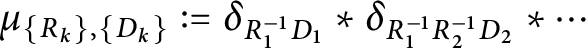$$ \begin{align*} \mu_{\{R_{k}\},\{D_{k}\}}:=\delta_{R_{1}^{-1}D_{1}}\ast\delta_{R_{1}^{-1}R_{2}^{-1}D_{2}}\ast\cdots \end{align*} $$
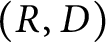is a spectral measure. For the converse, we get a necessity condition for the admissible pair $(R,D)$ .

Keywords

AdmissibleHadamard tripleMoran measureinfinite convolutionorthonormal basis of exponentialspectral measures

MSC classification

Primary: 28A80: Fractals
Secondary: 42C05: Orthogonal functions and polynomials, general theory 46C05: Hilbert and pre-Hilbert spaces
Type
Article
Information
Canadian Mathematical Bulletin , Volume 66 , Issue 1 , March 2023 , pp. 269 - 285
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported by the National Natural Science Foundation of China 11971194.

References

An, L.-X., Fu, X.-Y., and Lai, C.-K., On spectral Cantor–Moran measures and a variant of Bourgain’s sum of sine problem . Adv. Math. 349(2019), 84–124.CrossRefGoogle Scholar
An, L.-X. and He, X.-G., A class of spectral Moran measures . J. Funct. Anal. 266(2014), 343–354.CrossRefGoogle Scholar
Dai, X.-R., When does a Bernoulli convolution admit a spectrum? Adv. Math. 231(2012), 1681–1693.CrossRefGoogle Scholar
Dai, X.-R., Fu, X.-Y., and Yan, Z.-H., Spectrality of self-affine Sierpinski-type measures on  ${\mathbb{R}}^2$ . Appl. Comput. Harmon. Anal. 52(2021), 63–81.CrossRefGoogle Scholar
Dai, X.-R., He, X.-G., and Lai, C.-K., Spectral property of Cantor measures with consecutive digits . Adv. Math. 242(2013), 187–208.CrossRefGoogle Scholar
Dai, X.-R., He, X.-G., and Lau, K.-S., On spectral N-Bernoulli measures . Adv. Math. 259(2014), 511–531.CrossRefGoogle Scholar
Deng, Q.-R. and Lau, K.-S., Sierpinski-type spectral self-similar measures . J. Funct. Anal. 268(2015), 1310–1326.CrossRefGoogle Scholar
Dutkay, D., Emami, S., and Lai, C.-K., Existence and exactness of exponential Riesz sequences and frames for fractal measures . J. Anal. Math. 143(2021), 289–311.CrossRefGoogle Scholar
Dutkay, D., Han, D., and Sun, Q., On the spectra of a Cantor measure . Adv. Math. 221(2009), 251–276.CrossRefGoogle Scholar
Dutkay, D., Haussermann, J., and Lai, C.-K., Hadamard triples generate self-affine spectral measuresąč . Trans. Amer. Math. Soc. 371(2019), 1439–1481.CrossRefGoogle Scholar
Falconer, K. J., Fractal geometry: mathematical foundations and applications, Wiley, New York, 1990.Google Scholar
Fu, Y.-S. and Wen, Z.-X., Spectrality property of a class of Moran measures on  $\mathbb{R}$ . J. Math. Anal. Appl. 430(2015), 572–584.CrossRefGoogle Scholar
Fu, Y.-S. and Wen, Z.-X., Spectrality of infinite convolutions with three-element digit sets . Monatsh. Math. 183(2017), 465–485.CrossRefGoogle Scholar
Fuglede, B., Commuting self-adjoint partial differential operators and a group theoretic problem . J. Funct. Anal. 16(1974), 101–121.CrossRefGoogle Scholar
He, L. and He, X.-G., On the Fourier orthonormal basis of Cantor–Moran measure . J. Funct. Anal. 272(2017), 1980–2004.CrossRefGoogle Scholar
Hu, T. Y. and Lau, K. S., Spectral property of the Bernoulli convolution . Adv. Math. 219(2008), 554–567.CrossRefGoogle Scholar
Jacod, J. and Protter, P., Probability essentials. 2nd ed., Universitext, Springer, Berlin, 2003.Google Scholar
Jorgensen, P. and Pedersen, S., Dense analytic subspaces in fractal L 2 spaces . J. Anal. Math. 75(1998), 185–228.CrossRefGoogle Scholar
Jorgensen, P. and Pedersen, S., Orthogonal harmonic analysis of fractal measures . Electron. Res. Announc. Amer. Math. Soc. 4(1998), 35–42.CrossRefGoogle Scholar
Kolountzakis, M. and Matolcsi, M., Complex Hadamard matrices and the spectral set conjecture . Collect. Math. Extra(2006), 281–291.Google Scholar
Kolountzakis, M. and Matolcsi, M., Tiles with no spectra . Forum Math. 18(2006), 519–528.CrossRefGoogle Scholar
Łaba, I. and Wang, Y., On spectral Cantor measures . J. Funct. Anal. 193(2002), 409–420.CrossRefGoogle Scholar
Li, J.-L., ${\mu}_{M,D}-$ orthogonality and compatible pair . J. Funct. Anal. 244(2007), 628–638.CrossRefGoogle Scholar
Li, J.-L., Spectral of a class self-affine measures . J. Funct. Anal. 260(2011), 1086–1095.CrossRefGoogle Scholar
Liu, J. and Luo, J., Spectral property of self-affine measures on  ${\mathbb{R}}^n$ . J. Funct. Anal. 272(2017), 599–612.CrossRefGoogle Scholar
Liu, Z.-S. and Dong, X.-H., Spectra of a class of Moran measures (Chinese) . Adv. Math. (China) 47(2018), 441–447.Google Scholar
Stricharz, R., Fourier asymptotics of fractal measures . J. Funct. Anal. 89(1990), 154–187.CrossRefGoogle Scholar
Stricharz, R., Self-similarity in harmonic analysis . J. Fourier Anal. Appl. 1(1994), 1–37.CrossRefGoogle Scholar
Stricharz, R., Mock Fourier series and transforms associated with certain Cantor measures . J. Anal. Math. 81(2000), 209–238.CrossRefGoogle Scholar
Tao, T., Fuglede’s conjecture is false in 5 or higher dimensions . Math. Res. Lett. 11(2004), 251–258.CrossRefGoogle Scholar