Let 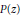$P\left( z \right)$ be a polynomial of degree not exceeding $n$ and let 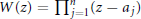$W\left( z \right)\,=\,\prod\nolimits_{j=1}^{n}{\left( z\,-\,{{a}_{j}} \right)}$ where 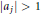$\left| {{a}_{j}} \right|\,>\,1$, 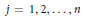$j\,=\,1,\,2,\,.\,.\,.\,,\,n$. If the rational function 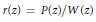$r\left( z \right)\,=\,{P\left( z \right)}/{W\left( z \right)}\;$ does not vanish in 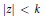$\left| z \right|\,<\,k$, then for 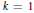$k\,=\,1$ it is known that

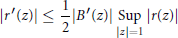$$\left| {{r}^{'}}\left( z \right) \right|\le \frac{1}{2}\left| {{B}^{'}}(z) \right|_{\left| z \right|=1}^{\text{Sup}}\left| r(z) \right|$$

where 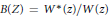$B\left( Z \right)\,=\,{{{W}^{*}}\left( z \right)}/{W\left( z \right)}\;$ and ${{W}^{*}}\left( z \right)\,=\,{{z}^{n}}\overline{W\left( {1}/{\overline{z}}\; \right)}$. In the paper we consider the case when $k\,>\,1$ and obtain a sharp result. We also show that

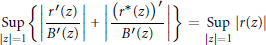$$\underset{\left| z \right|=1}{\mathop{\text{Sup}}}\,\left\{ \left| \frac{{{r}^{\prime }}\left( z \right)}{{{B}^{\prime }}\left( z \right)} \right|+\left| \frac{{{\left( {{r}^{*}}\left( z \right) \right)}^{\prime }}}{{{B}^{\prime }}\left( z \right)} \right| \right\}=\underset{\left| z \right|=1}{\mathop{\text{Sup}}}\,\left| r\left( z \right) \right|$$

where 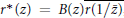${{r}^{*}}\left( z \right)\,=\,B\left( z \right)\overline{r\left( {1}/{\overline{z}}\; \right)}$, and as a consquence of this result, we present a generalization of a theorem of O’Hara and Rodriguez for self-inversive polynomials. Finally, we establish a similar result when supremum is replaced by infimum for a rational function which has all its zeros in the unit circle.