Hostname: page-component-84b7d79bbc-l82ql Total loading time: 0 Render date: 2024-07-25T14:46:39.642Z Has data issue: false hasContentIssue false
  • English
  • Français

Remarques sur l’enlacement en théorie des points critiques pour des fonctionnelles continues

Published online by Cambridge University Press:  20 November 2018

M. Frigon
M. Frigon*
Affiliation:
Département de mathématiques et statistique Université de Montréal C. P. 6128, Succ. Centre-ville Montréal, QC H3C 3J7, e-mail: frigon@dms.umontreal.ca
Rights & Permissions [Opens in a new window]

Résumé

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Dans cet article, à partir de la notion d’enlacement introduite dans [7] entre des paires d’ensembles 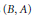$(B,\,A)$ et 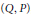$(Q,\,P)$, nous établissons l’existence d’un point critique d’une fonctionnelle continue sur un espace métrique lorsqu’une de ces paires enlace l’autre. Des renseignements sur la localisation du point critique sont aussi obtenus. Ces résultats conduisent à une généralisation du théorème des trois points critiques. Finalement, des applications à des problèmes aux limites pour une équation quasi-linéaire elliptique sont présentées.

Abstract

Abstract

In this paper, from the linking notion for pairs 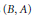$(B,\,A)$ and 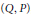$(Q,\,P)$ introduced in [7], the existence of a critical point of a continuous functional defined on ametric space is established when one of these pairs links the other. Information on the location of the critical point leads to a generalization of the three critical points Theorem. Finally, applications to elliptic quasi-linear equations are presented.

Keywords

58E0535J20
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 47 , Issue 4 , 01 December 2004 , pp. 515 - 529
Copyright
Copyright © Canadian Mathematical Society 2004

References

Références

[1] Benci, V. et Rabinowitz, P. H., Critical point theorems for indefinite functionals. Invent.Math. 52 (1979), 241–273.Google Scholar
[2] Brezis, H. et Nirenberg, L., Remarks on finding critical points. Comm. Pure Appl. Math. 64 (1991), 939–963.Google Scholar
[3] Canino, A. et Degiovanni, M., Nonsmooth critical point theory and quasilinear elliptic equations, Topological methods in differential equations and inclusions, NATO Adv. Sci. Inst. Series, Ser. C Math. and Phys. Sci., 472, Kluwer, Dordrecht, 1995, pp. 1–50.Google Scholar
[4] Corvellec, J.-N., On critical point theory with the (PS)* condition, Calculus of variations and differential equations. (A. Ioffe, S. Reich and I. Shafrir, eds.) Chapman Ȧ Hall/CRC Research Notes in Mathematics, 410, CRC Press, Boca Raton, FL, 2000, pp. 65–81.Google Scholar
[5] Corvellec, J.-N., Degiovanni, M. et Marzocchi, M., Deformation properties for continuous functionals and critical point theory. Topol. Methods Nonlinear Anal. 1 (1993), 151–171.Google Scholar
[6] Degiovanni, M. et Marzocchi, M., A critical point theory for nonsmooth functionals. Ann. Mat. Pura Appl. (4) 167 (1994), 73–100.Google Scholar
[7] Frigon, M., On a new notion of linking and application to elliptic problems at resonance. J. Differential Equations 153 (1999), 96–120.Google Scholar
[8] Ghoussoub, N., Location, multiplicity and Morse indices of min-max critical points. J. Reine Angew. Math. 417 (1991), 27–76.Google Scholar
[9] Li, S. et Willem, M., Applications of local linking to critical point theory. J. Math. Anal. Appl. 189 (1995), 6–32.Google Scholar
[10] Liu, J. Q. et Li, S. J., Some existence theorems on multiple critical points and their applications. Kexue Tongbao 17 (1984), 1025–1027.Google Scholar
[11] Picard, F., Généralisation de résultats sur l’enlacement local en théorie des points critiques. Mémoire de mâıtrise, Université de Montréal,Montréal, 1999. 65 Amer.Math. Soc., Providence, RI, 1986.Google Scholar
[12] Schechter, M. et Tintarev, K., Pairs of critical points produced by linking subsets with applications to semilinear elliptic problems. Bull. Soc. Math. Belg. Sér. B 44 (1992), 249–261.Google Scholar
[13] Schechter, M., Infinite dimensional linking. Duke Math. J. 94 (1998), 573–595.Google Scholar