Hostname: page-component-848d4c4894-wzw2p Total loading time: 0 Render date: 2024-05-06T04:56:22.819Z Has data issue: false hasContentIssue false
  • English
  • Français

A Reduction of the Batyrev-Manin Conjecture for Kummer Surfaces

Published online by Cambridge University Press:  20 November 2018

David McKinnon
David McKinnon*
Affiliation:
Department of Pure Mathematics University of Waterloo Waterloo, ON N2T 2M2, e-mail: dmckinno@math.uwaterloo.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 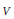$V$ be a 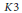$K3$ surface defined over a number field 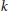$k$. The Batyrev-Manin conjecture for 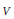$V$ states that for every nonempty open subset 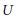$U$ of 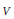$V$, there exists a finite set 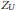${{Z}_{U}}$ of accumulating rational curves such that the density of rational points on 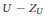$U\,-\,{{Z}_{U}}$ is strictly less than the density of rational points on 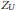${{Z}_{U}}$. Thus, the set of rational points of 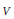$V$ conjecturally admits a stratification corresponding to the sets 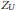${{Z}_{U}}$ for successively smaller sets 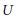$U$.

In this paper, in the case that 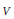$V$ is a Kummer surface, we prove that the Batyrev-Manin conjecture for 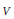$V$ can be reduced to the Batyrev-Manin conjecture for 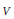$V$ modulo the endomorphisms of 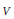$V$ induced by multiplication by 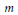$m$ on the associated abelian surface 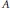$A$. As an application, we use this to show that given some restrictions on 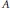$A$, the set of rational points of 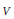$V$ which lie on rational curves whose preimages have geometric genus 2 admits a stratification of Batyrev-Manin type.

Keywords

11G3514G05rational pointsBatyrev-Manin conjectureKummer surfacerational curveabelian surfaceheight
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 47 , Issue 3 , 01 September 2004 , pp. 398 - 406
Copyright
Copyright © Canadian Mathematical Society 2004

References

[1] Billard, H., Propriétés arithmétiques d’une famille de surfaces K3, Compositio Math. 108 (1997), 247–275.Google Scholar
[2] Batyrev, V. and Manin, Yu., Sur le nombre de points rationnels de hauteur borné des variétés algébriques, Math. Ann. 286 (1990), 27–43.Google Scholar
[3] Call, G., Counting geometric points on families of abelian varieties, Math. Nachr. 166 (1994), 167–192.Google Scholar
[4] Colombo, E. and Pirola, G. P., Some density results for curves with non-simple Jacobians, Math. Ann. 288 (1990), 161–178.Google Scholar
[5] Faltings, G., Endlichkeitssätze für abelsche Varietäten über Zahlkörpern, Invent.Math. 73 (1983), 349–366.Google Scholar
[6] King, H., and Todorov, A., Rational points on some Kummer surfaces, preprint (1992).Google Scholar
[7] McKinnon, D., Counting rational points on K3 surfaces, J. Number Theory 84 (2000), 49–62.Google Scholar
[8] Milne, J., Abelian varieties. In: Arithmetic Geometry, (eds. G. Cornell and J. Silverman), Springer-Verlag, New York, 1986, pp. 103–150.Google Scholar
[9] Milne, J., Jacobian varieties. In: Arithmetic Geometry, (eds. G. Cornell and J. Silverman), Springer-Verlag, New York, 1986, pp. 167–212.Google Scholar
[10] Sato, A., On the distribution of rational points on certain Kummer surfaces, Acta Arith. 86 (1998), 1–16.Google Scholar
[11] Schanuel, S., Heights in number fields, Bull. Soc. Math. France 107 (1979), 433–449.Google Scholar
[12] Silverman, J., Computing heights on K3 surfaces: a new canonical height, Invent.Math. 105 (1991), 347–373.Google Scholar
[13] Vojta, P., Diophantine Approximations and Value Distribution Theory, Lecture Notes in Math. 1239, Springer-Verlag, New York, 1987.Google Scholar