Hostname: page-component-848d4c4894-xm8r8 Total loading time: 0 Render date: 2024-06-23T09:46:54.489Z Has data issue: false hasContentIssue false
  • English
  • Français

Ramanujan-type series for 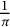$\frac {1}{\pi }$, revisited

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  05 October 2023

Dongxi Ye Open the ORCID record for Dongxi Ye [Opens in a new window]
Dongxi Ye*
Affiliation:
School of Mathematics (Zhuhai), Sun Yat-sen University, Zhuhai, Guangdong 519082, China
*
e-mail: yedx3@mail.sysu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

In this note, we revisit Ramanujan-type series for 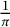$\frac {1}{\pi }$ and show how they arise from genus zero subgroups of 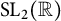$\mathrm {SL}_{2}(\mathbb {R})$ that are commensurable with 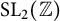$\mathrm {SL}_{2}(\mathbb {Z})$. As illustrations, we reproduce a striking formula of Ramanujan for 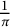$\frac {1}{\pi }$ and a recent result of Cooper et al., as well as derive a new rational Ramanujan-type series for 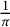$\frac {1}{\pi }$. As a byproduct, we obtain a Clausen-type formula in some general sense and reproduce a Clausen-type quadratic transformation formula closely related to the aforementioned formula of Ramanujan.

Keywords

Orbifold uniformizations1⁄πClausen-type transformations

MSC classification

Primary: 11F03: Modular and automorphic functions 11F23: Relations with algebraic geometry and topology
Type
Article
Information
Canadian Mathematical Bulletin , Volume 67 , Issue 2 , June 2024 , pp. 350 - 368
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported by the Guangdong Basic and Applied Basic Research Foundation (Grant No. 2023A1515010298).

References

Almkvist, G. and Zudilin, W., Differential equations, mirror maps and zeta values . In: Mirror symmetry. V, AMS/IP Studies in Advanced Mathematics, 38, American Mathematical Society, Providence, RI, 2006, pp. 481–515.Google Scholar
Anusha, T., Bhuvan, E. N., Cooper, S., and Vasuki, K. R., Elliptic integrals and Ramanujan-type series for $1/ \unicode{x3c0}$ associated with ${\Gamma}_0(\mathrm{N})$ , where $\mathrm{N}$ is a product of two small primes. J. Math. Anal. Appl. 472(2019), no. 2, 1551–1570.CrossRefGoogle Scholar
Baruah, N. D., Berndt, B. C., and Chan, H. H., Ramanujan’s series for $1/ \pi$ : a survey . Amer. Math. Mon. 116(2009), 567–587.CrossRefGoogle Scholar
Beardon, A. F., The geometry of discrete groups, Springer, New York, 1983.CrossRefGoogle Scholar
Chan, H. H., Chan, S. H., and Liu, Z., Domb’s numbers and Ramanujan–Sato type series for $1/ \pi$ . Adv. Math. 186(2004), no. 2, 396–410.CrossRefGoogle Scholar
Chan, H. H. and Cooper, S., Rational analogues of Ramanujan’s series for $1/ \pi$ . Math. Proc. Camb. Phil. Soc. 153(2012), 361–383.CrossRefGoogle Scholar
Chan, H. H., Tanigawa, Y., Yang, Y., and Zudilin, W., New analogues of Clausen’s identities arising from the theory of modular forms . Adv. Math. 228(2011), no. 2, 1294–1314.CrossRefGoogle Scholar
Cohen, H. and Strömberg, F., Modular forms: a classical approach, American Mathematical Society, Providence, RI, 2017.CrossRefGoogle Scholar
Cooper, S., Ramanujan’s theta functions, Springer, Cham, 2017.CrossRefGoogle Scholar
Ramanujan, S., Modular equations and approximations to $\pi$ . Quart. J. Math. 45(1914), 350–372.Google Scholar
Singer, M., Algebraic relations among solutions of linear differential equations: Fano’s theorem . Amer. J. Math. 110(1988), no. 1, 115–143.CrossRefGoogle Scholar
Yoshida, M., Fuchsian differential equations. With special emphasis on the Gauss–Schwarz theory, Aspects of Mathematics, E11, Friedr. Vieweg & Sohn, Braunschweig, 1987, xiv + 215 pp.CrossRefGoogle Scholar