Hostname: page-component-77c89778f8-7drxs Total loading time: 0 Render date: 2024-07-17T02:51:55.375Z Has data issue: false hasContentIssue false
  • English
  • Français

On 3-manifolds with Torus or Klein Bottle Category Two

Published online by Cambridge University Press:  20 November 2018

Wolfgang Heil  and
Dongxu Wang
Wolfgang Heil
Affiliation:
Department of Mathematics, Florida State University, Tallahassee, Florida 32306, USA e-mail: heil@math.fsu.edudxwang1981@gmail.com
Dongxu Wang
Affiliation:
Department of Mathematics, Florida State University, Tallahassee, Florida 32306, USA e-mail: heil@math.fsu.edudxwang1981@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A subset 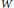$W$ of a closed manifold 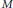$M$ is $K$-contractible, where $K$ is a torus or Klein bottle if the inclusion 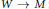$W\,\to \,M$ factors homotopically through a map to $K$. The image of 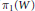${{\pi }_{1}}\left( W \right)$ (for any base point) is a subgroup of 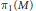${{\pi }_{1}}\left( M \right)$ that is isomorphic to a subgroup of a quotient group of 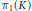${{\pi }_{1}}\left( K \right)$. Subsets of 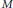$M$ with this latter property are called 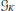${{\mathcal{G}}_{K}}$-contractible. We obtain a list of the closed 3-manifolds that can be covered by two open 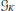${{\mathcal{G}}_{K}}$-contractible subsets. This is applied to obtain a list of the possible closed prime 3-manifolds that can be covered by two open $K$-contractible subsets.

Keywords

57N1055M3057M2757N16Lusternik–Schnirelmann categorycoverings of 3-manifolds by open K-contractible sets
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 3 , 01 September 2014 , pp. 526 - 537
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Bessiçres, L., Besson, G., Maillot, S., Boileau, M., and Porti, J., Geometrisation of 3-Manifolds. EMS Tracts in Mathematics, 13, European Mathematical Society, Zürich, 2010.Google Scholar
[2] Clapp, M. and Puppe, D., Invariants of the Lusternik-Schnirelmann type and the topology of critical sets. Trans. Amer. Math. Soc. 298 (1986), no. 2, 603–620. http://dx.doi.org/10.1090/S0002-9947-1986-0860382-0 Google Scholar
[3] Cornea, O., Lupton, G., Oprea, J., and D. Tanr´e, Lusternik-Schnirelman category. Mathematical Surveys and Monographs, 103, American Mathematical Society, Providence, RI, 2003.Google Scholar
[4] Gömez-Larrañaga, J. C., González-Acuna, F., and Heil, W., Fundamental groups manifolds with S1-category 2. Math Z. 259 (2008), no. 2, 419–432.Google Scholar
[5] Gömez-Larrañaga, J. C., González-Acuna, F., and Heil, W., 3-manifolds that are covered by two open bundles. Bol. Soc. Mat. Mexicana (3) 10 (2004), Special issue, 171–179.Google Scholar
[6] Gömez-Larrañaga, J. C., González-Acuna, F., and Heil, W., S2- and P2-category of manifolds. Topology Appl. 159 (2012), no. 4, 1052–1058.Google Scholar
[7] Gömez-Larrañaga, J. C., González-Acuna, F., and Heil, W., Amenable categories of three-manifolds. Algebre. Geom. Topol. 13 (2013), no. 2, 905–925.Google Scholar
[8] Gömez-Larrañaga, J. C., González-Acuna, F., and Heil, W., On the K-category of 3-manifolds for K a wedge of spheres or projective planes. Topol. Proc. 44 (2014), 49–58. (E-published on May 24, 2013)Google Scholar
[9] Gömez-Larrañaga, J. C., González-Acuna, F., and Heil, W., Categorical group invariants of 3-manifolds. http://www.math.fsu.edu/_aluffi/archive/paper437.pdfGoogle Scholar
[10] Hatcher, A., Notes on basic 3-manifold Topology. Lecture Notes. http://www.math.cornell.edu/_hatcher. Google Scholar
[11] Hempel, J., 3-manifolds. Ann. of Math., 86, Princeton University Press, Princeton, NJ, 1976.Google Scholar
[12] Matijević, V., Finite-sheeted covering maps over Klein bottle weak solenoidal spaces. Glas. Mat. Ser. III 42 (62) (2007), no. 1, 19–41. http://dx.doi.org/10.3336/gm.42.1.02 Google Scholar
[13] Milnor, J., Groups which act without fixed points on Sn. Amer. J. Math. 79 (1957), 623–630. http://dx.doi.org/10.2307/2372566 Google Scholar
[14] Orlik, P., Seifert manifolds. Lecture Notes in Mathematics, 291, Springer-Verlag, Berlin-New York, 1972 Google Scholar