Hostname: page-component-5c6d5d7d68-xq9c7 Total loading time: 0 Render date: 2024-08-07T05:15:04.434Z Has data issue: false hasContentIssue false
  • English
  • Français

Nilpotent Group C*-algebras as Compact Quantum Metric Spaces

Published online by Cambridge University Press:  20 November 2018

Michael Christ  and
Marc A. Rieòel
Michael Christ
Affiliation:
Department of Mathematics, University of California, Berkeley, CA 94720-3840 e-mail: mchrist@math.berkeley.edu e-mail: rieffel@math.berkeley.edu
Marc A. Rieòel
Affiliation:
Department of Mathematics, University of California, Berkeley, CA 94720-3840 e-mail: mchrist@math.berkeley.edu e-mail: rieffel@math.berkeley.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $\mathbb{L}$ be a length function on a group $G$, and let 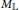${{M}_{\mathbb{L}}}$ denote the operator of pointwise multiplication by $\mathbb{L}$ on 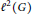${{\ell }^{2}}\left( G \right)$. Following Connes, 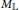${{M}_{\mathbb{L}}}$ can be used as a “Dirac” operator for the reduced group 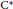${{C}^{*}}$-algebra 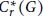$C_{r}^{*}\left( G \right)$. It defines a Lipschitz seminorm on 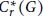$C_{r}^{*}\left( G \right)$, which defines a metric on the state space of 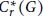$C_{r}^{*}\left( G \right)$. We show that for any length function satisfying a strong form of polynomial growth on a discrete group, the topology from this metric coincides with the weak-$*$ topology (a key property for the definition of a “compact quantum metric space”). In particular, this holds for all word-length functions on finitely generated nilpotent-by-finite groups.

Keywords

46L8720F6522D1553C2358B34group C*-algebraDirac operatorquantummetric spacediscrete nilpotent grouppolynomial growth
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 60 , Issue 1 , 01 March 2017 , pp. 77 - 94
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Antonescu, C. and Christensen, E., Metrics on group C*-algebras and a non-commutative Arzelà-Ascoli theorem. J. Funct. Anal. 214(2004), 247–259. http://dx.doi.Org/1 0.101 6/j.jfa.2 004.04.01 5 Google Scholar
[2] Bass, H., The degree of polynomial growth of finitely generated nilpotent groups. Proc. London Math. Soc. 25(1972), 603–614. http://dx.doi.Org/10.1112/plms/s3-25.4.603 Google Scholar
[3] Christ, M., Inversion in some algebras of singular integral operators. Rev. Mat. Iberoamericana 4(1988), 219–225. http://dx.doi.Org/10.4171/RMI/72 Google Scholar
[4] Christ, M., On the regularity of inverses of singular integral operators. Duke Math. J. 57(1988), 459–484. http://dx.doi.Org/10.1215/S0012-7094-88-05721-3 Google Scholar
[5] Connes, A., C* algebres et géométrie différentielle. C. R. Acad. Sci. Paris Sér. A-B 290(1980), no. 13, A599-A604.Google Scholar
[6] Connes, A., Compact metric spaces, Fredholm modules, and hyperfiniteness. Ergodic Theory Dynam. Systems 9(1989), 207–220. http://dx.doi.Org/10.101 7/S0143385700004934 Google Scholar
[7] de la Harpe, P., Groupes hyperboliques, algèbres d'opérateurs et un théorème de folissaint. C. R. Acad. Sci. Paris Sér. I Math. 307(1988), no. 14, 771–774.Google Scholar
[8] Gromov, M., Groups of polynomial growth and expanding maps. Inst. Hautes Études Sci. Publ. Math. 53(1981), 53–73.Google Scholar
[9] Jolissaint, P., Rapidly decreasing functions in reduced C*-algebras of groups. Trans. Amer. Math. Soc. 317(1990), no. 1, 167–196. http://dx.doi.Org/! 0.2307/2001458 Google Scholar
[10] Kleiner, B., A new proof of Gromov's theorem on groups of polynomial growth. J. Amer. Math. Soc. 23(2010), no. 3, 815–829. http://dx.doi.Org/10.1 090/S0894-0347-09-00658-4 Google Scholar
[11] Mann, A., How groups grow. London Mathematical Society Lecture Note Series, 395, Cambridge University Press, Cambridge, 2012.Google Scholar
[12] Ozawa, N., A functional analysis proof of Gromov's polynomial growth theorem. arxiv:1510.0422.Google Scholar
[13] Ozawa, N. and Rieffel, M. A., Hyperbolic group C*-algebras and free-product C*-algebras as compact quantum metric spaces. Canad. J. Math. 57(2005), no. 5,1056-1079. http://dx.doi.Org/1 0.41 53/CJM-2005-040-0 Google Scholar
[14] Packer, J. A., C*-algebras generated by protective representations of the discrete Heisenberg group. J. Operator Theory 18(1987), no. 1, 41–66.Google Scholar
[15] Packer, J. A., Twisted group C*-algebras corresponding to nilpotent discrete groups. Math. Scand. 64(1989), 109–122.Google Scholar
[16] Paterson, A. L. T., Amenability. Mathematical Surveys and Monographs, 29, American Mathematical Society, Providence, RI, 1988. http://dx.doi.Org/10.1090/surv/029 Google Scholar
[17] Rieffel, M. A., Proper actions of groups on C*-algebras. In: Mappings of operator algebras (Philadelphia, PA, 1988), Progr. Math., 84, Birkhauser Boston, Boston, MA, 1990, pp. 141–182.Google Scholar
[18] Rieffel, M. A., Metrics on states from actions of compact groups. Doc. Math. 3(1998), 215–229. arXiv:math.OA/9807084.Google Scholar
[19] Rieffel, M. A., Metrics on state spaces. Doc. Math. 4(1999), 559–600.Google Scholar
[20] Rieffel, M. A., Group C*-algebras as compact quantum metric spaces. Doc. Math. 7(2002), 605–651.Google Scholar
[21] Rieffel, M. A., Gromov-Hausdorff distance for quantum metric spaces. Mem. Amer. Math. Soc. 168(2004), no. 796, 1-65. http://dx.doi.Org/10.1090/memo/0796 Google Scholar
[22] Rieffel, M. A., Integrable and proper actions on C*-algebras, and square-integrable representations of groups. Expo. Math. 22(2004), 1–53. http://dx.doi.Org/10.101 6/S0723-0869(04)80002-1 Google Scholar
[23] Rieffel, M. A., Matrix algebras converge to the sphere for quantum Gromov-Hausdorff distance. Mem. Amer. Math. Soc. 168(2004), no. 796, 67–91. http://dx.doi.Org/10.1090/memo/0796 Google Scholar
[24] Rieffel, M. A., Leibniz seminorms for “Matrix algebras converge to the sphere”. In: Quanta of maths, Clay Math. Proa, 11, American Mathematical Society, Providence, RI, 2011, pp. 543–578.Google Scholar
[25] Rieffel, M. A., Matricial bridges for “matrix algebras converge to the sphere”. Contemp. Math., to appear. arxiv:1 502.0032.Google Scholar
[26] Shalom, Y. and Tao, T., A finitary version of Gromov's polynomial growth theorem. Geom. Funct. Anal. 20(2010), no. 6, 1502–1547. http://dx.doi.Org/10.1007/s00039-010-0096-1 Google Scholar
[27] Wolf, J. A., Growth of finitely generated solvable groups and curvature of Riemanniann manifolds. J. Differential Geometry 2(1968), 421–446.Google Scholar