Article contents
Maximal Weight Composition Factors for Weyl Modules
Published online by Cambridge University Press: 20 November 2018
Abstract
Fix an irreducible (finite) root system  $R$ and a choice of positive roots. For any algebraically closed field
$R$ and a choice of positive roots. For any algebraically closed field  $k$ consider the almost simple, simply connected algebraic group
$k$ consider the almost simple, simply connected algebraic group 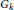 ${{G}_{k}}$ over
${{G}_{k}}$ over  $k$ with root system
$k$ with root system  $k$. One associates with any dominant weight
$k$. One associates with any dominant weight  $\lambda $ for
$\lambda $ for  $R$ two
$R$ two 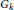 ${{G}_{k}}$-modules with highest weight
${{G}_{k}}$-modules with highest weight  $\lambda $, the Weyl module
$\lambda $, the Weyl module 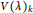 $V{{(\lambda )}_{k}}$ and its simple quotient
$V{{(\lambda )}_{k}}$ and its simple quotient 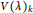 $V{{(\lambda )}_{k}}$. Let
$V{{(\lambda )}_{k}}$. Let  $\lambda $ and
$\lambda $ and  $\mu $ be dominant weights with
$\mu $ be dominant weights with 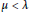 $\mu <\lambda $ such that
$\mu <\lambda $ such that  $\mu $ is maximal with this property. Garibaldi, Guralnick, and Nakano have asked under which condition there exists
$\mu $ is maximal with this property. Garibaldi, Guralnick, and Nakano have asked under which condition there exists  $k$ such that
$k$ such that  $L{{(\mu )}_{k}}$ is a composition factor of
$L{{(\mu )}_{k}}$ is a composition factor of 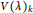 $V{{(\lambda )}_{k}}$, and they exhibit an example in type
$V{{(\lambda )}_{k}}$, and they exhibit an example in type 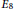 ${{E}_{8}}$ where this is not the case. The purpose of this paper is to to show that their example is the only one. It contains two proofs for this fact: one that uses a classiffication of the possible pairs
${{E}_{8}}$ where this is not the case. The purpose of this paper is to to show that their example is the only one. It contains two proofs for this fact: one that uses a classiffication of the possible pairs 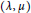 $(\lambda ,\mu )$, and another that relies only on the classiûcation of root systems.
$(\lambda ,\mu )$, and another that relies only on the classiûcation of root systems.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2017
References
- 1
- Cited by




