No CrossRef data available.
Article contents
The Geometry of d2y1/dt2 = f (y, ẏ, t) and d2y2/dt2 = g(y, ẏ, t), and Euclidean Spaces
Published online by Cambridge University Press: 20 November 2018
Abstract
This paper investigates the relationship between a system of differential equations and the underlying geometry associated with it. The geometry of a surface determines shortest paths, or geodesics connecting nearby points, which are defined as the solutions to a pair of second-order differential equations: the Euler–Lagrange equations of the metric. We ask when the converse holds, that is, when solutions to a system of differential equations reveals an underlying geometry. Specifically, when may the solutions to a given pair of second order ordinary differential equations 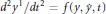 ${{d}^{2}}{{y}^{1}}/d{{t}^{2}}=f\left( y,\dot{y},t \right)$ and
${{d}^{2}}{{y}^{1}}/d{{t}^{2}}=f\left( y,\dot{y},t \right)$ and 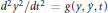 ${{d}^{2}}{{y}^{2}}/d{{t}^{2}}=g\left( y,\dot{y},t \right)$ be reparameterized by
${{d}^{2}}{{y}^{2}}/d{{t}^{2}}=g\left( y,\dot{y},t \right)$ be reparameterized by 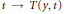 $t\to T\left( y,t \right)$ so as to give locally the geodesics of a Euclidean space? Our approach is based upon Cartan's method of equivalence. In the second part of the paper, the equivalence problem is solved for a generic pair of second order ordinary differential equations of the above form revealing the existence of 24 invariant functions.
$t\to T\left( y,t \right)$ so as to give locally the geodesics of a Euclidean space? Our approach is based upon Cartan's method of equivalence. In the second part of the paper, the equivalence problem is solved for a generic pair of second order ordinary differential equations of the above form revealing the existence of 24 invariant functions.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2006




