Article contents
Generalized Equivariant Cohomology and Stratifications
Published online by Cambridge University Press: 20 November 2018
Abstract
For 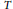 $T$ a compact torus and
$T$ a compact torus and 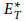 $E_{T}^{*}$ a generalized
$E_{T}^{*}$ a generalized 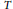 $T$-equivariant cohomology theory, we provide a systematic framework for computing
$T$-equivariant cohomology theory, we provide a systematic framework for computing 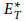 $E_{T}^{*}$ in the context of equivariantly stratified smooth complex projective varieties. This allows us to explicitly compute
$E_{T}^{*}$ in the context of equivariantly stratified smooth complex projective varieties. This allows us to explicitly compute 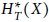 $H_{T}^{*}\left( X \right)$ as an
$H_{T}^{*}\left( X \right)$ as an 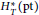 $H_{T}^{*}\left( pt \right)$-module when
$H_{T}^{*}\left( pt \right)$-module when  $X$ is a direct limit of smooth complex projective
$X$ is a direct limit of smooth complex projective 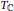 ${{T}_{\mathbb{C}}}$-varieties. We perform this computation on the affine Grassmannian of a complex semisimple group.
${{T}_{\mathbb{C}}}$-varieties. We perform this computation on the affine Grassmannian of a complex semisimple group.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2016
References
- 1
- Cited by




