Hostname: page-component-77c89778f8-9q27g Total loading time: 0 Render date: 2024-07-22T05:35:06.603Z Has data issue: false hasContentIssue false
  • English
  • Français

A Determinantal Inequality Involving Partial Traces

Published online by Cambridge University Press:  20 November 2018

Minghua Lin
Minghua Lin*
Affiliation:
Department of Mathematics, Shanghai University, Shanghai 20044, China e-mail: m_lin@shu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

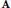Let $\mathbf{A}$ be a density matrix in ${{\mathbb{M}}_{m}}\,\otimes \,{{\mathbb{M}}_{n}}$. Audenaert [J. Math. Phys. 48(2007) 083507] proved an inequality for Schatten 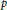$p$-norms:

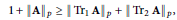$$1\,+\,||\mathbf{A}|{{|}_{p}}\,\ge \,{{\left\| \text{T}{{\text{r}}_{1}}\,\mathbf{A} \right\|}_{p}}\,+\,||\text{T}{{\text{r}}_{2}}\,\mathbf{A}|{{|}_{p}},$$

where $\text{T}{{\text{r}}_{1}}$ and $\text{T}{{\text{r}}_{2}}$ stand for the first and second partial trace, respectively. As an analogue of his result, we prove a determinantal inequality

$$1\,+\,\det \,\mathbf{A}\,\ge \,\det {{\left( \text{T}{{\text{r}}_{1}}\mathbf{A} \right)}^{m}}\,+\,\det {{\left( \text{T}{{\text{r}}_{2}}\mathbf{A} \right)}^{2}}.$$

Keywords

47B6515A4515A60determinantal inequalitypartial traceblock matrix
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 3 , 01 September 2016 , pp. 585 - 591
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Audenaert, K. M. R., Subadditivity of q-entropies for q > 1. J. Math. Phys. 48(2007), no. 8, 083507. http://dx.doi.org/10.1063/1.2 771542 +1.+J.+Math.+Phys.+48(2007),+no.+8,+083507.+http://dx.doi.org/10.1063/1.2+771542>Google Scholar
[2] Ando, T., Matrix inequalities involving partial traces. ILAS Conference, 2014. http://matrix.skku.ac.kr/!LAS-Book/Chapter3Abst.pdfGoogle Scholar
[3] Choi, M. D., Positive linear maps on C*-algebras. Canad. J. Math. 24(1972), 520–529. http://dx.doi.org/10.4153/CJM-1972-044-5 Google Scholar
[4] Choi, M. D., Completely positive linear maps on complex matrices. Linear Algebra Appl. 10(1975), 285–290. http://dx.doi.org/10.1016/0024-3795(75)90075-0 Google Scholar
[5] Horn, R. A. and Johnson, C. R., Matrix analysis. Second éd.,Cambridge University Press, Cambridge, 2013.Google Scholar
[6] Lin, M., An Oppenheim type inequality for a block Hadamard product. Linear Algebra Appl. 452(2014), 1–6. http://dx.doi.org/10.1016/j.laa.2014.03.025 Google Scholar
[7] Lin, M., A completely PPT map. Linear Algebra Appl. 459(2014), 404–410. http://dx.doi.org/10.1016/j.laa.2O14.07.040 Google Scholar
[8] Petz, D., Quantum information theory and quantum statistics. Theoretical and mathematical physics. Springer-Verlag, Berlin, 2008.Google Scholar
[9] van Dam, E. R., A Cauchy-Khinchin matrix inequality. Linear Algebra Appl. 280(1998), no. 2-3, 163-172. http://dx.doi.org/10.1016/S0024-3795(98)00019-6 Google Scholar