Hostname: page-component-848d4c4894-8kt4b Total loading time: 0 Render date: 2024-06-30T07:12:58.977Z Has data issue: false hasContentIssue false
  • English
  • Français

Connections Between Metric Characterizations of Superreflexivity and the Radon–Nikodým Property for Dual Banach Spaces

Published online by Cambridge University Press:  20 November 2018

Mikhail I. Ostrovskii
Mikhail I. Ostrovskii*
Affiliation:
Department of Mathematics and Computer Science, St. John’s University, 8000 Utopia Parkway, Queens, NY 11439, USA. e-mail: ostrovsm@stjohns.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Johnson and Schechtman (2009) characterized superreflexivity in terms of finite diamond graphs. The present author characterized the Radon–Nikodým property (RNP) for dual spaces in terms of the infinite diamond. This paper is devoted to further study of relations between metric characterizations of superreflexivity and the RNP for dual spaces. The main result is that finite subsets of any set 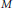$M$ whose embeddability characterizes the RNP for dual spaces, characterize superreflexivity. It is also observed that the converse statement does not hold and that 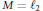$M\,=\,{{\ell }_{2}}$ is a counterexample.

Keywords

46B8546B0746B22Banach spacediamond graphfinite representabilitymetric characterizationRadon– Nikodym propertysuperreflexivity
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 1 , 01 March 2015 , pp. 150 - 157
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Amemiya, I. and Ito, T., Weakly null sequences in James spaces on trees. Kodai Math. J. 4 (1981), no. 3, 418–425. http://dx.doi.org/10.2996/kmj/1138036426 Google Scholar
[2] Beauzamy, B., Banach-Saks properties and spreading models. Math. Scand. 44 (1979), no. 2, 357–384. Google Scholar
[3] Benyamini, Y. and Lindenstrauss, J., Geometric nonlinear functional analysis. Vol. 1, American Mathematical Society Colloquium Publications, 48, American Mathematical Society, Providence, RI, 2000.Google Scholar
[4] Bellenot, S. F., Transfinite duals of quasireflexive Banach spaces. Trans. Amer. Math. Soc. 273 (1982), no. 2, 551–577. http://dx.doi.org/10.1090/S0002-9947-1982-0667160-2 Google Scholar
[5] Bourgain, J., Remarks on the extension of Lipschitz maps defined on discrete sets and uniform homeomorphisms. In: Geometrical aspects of functional analysis (1985/86), Lecture Notes in Math., 1267, Springer, Berlin, 1987, pp. 157–167..Google Scholar
[6] Brunel, A. and Sucheston, L., On B-convex Banach spaces. Math. Systems Theory 7 (1974), no. 4, 294–299. http://dx.doi.org/10.1007/BF01795947 Google Scholar
[7] Brunel, A. and Sucheston, L., On J-convexity and some ergodic super-properties of Banach spaces. Trans. Amer. Math. Soc. 204 (1975), 79–90. Google Scholar
[8] Brunel, A. and Sucheston, L., Equal signs additive sequences in Banach spaces. J. Funct. Anal. 21 (1976), no. 3, 286–304. http://dx.doi.org/10.1016/0022-1236(76)90041-0 Google Scholar
[9] Davis, W. J.,Johnson, W. B., and Lindenstrauss, J., The problem and degrees of non-reflexivity. Studia Math. 55 (1976), no. 2, 123–139. Google Scholar
[10] Davis, W. J. and Lindenstrauss, J., The problem and degrees of non-reflexivity. II. Studia Math. 58 (1976), no. 2, 179–196. Google Scholar
[11] Dvoretzky, A., Some results on convex bodies and Banach spaces. In: Proc. Internat. Sympos. Linear Spaces (Jerusalem, 1960), Jerusalem Academic Press, Jerusalem; Pergamon, Oxford, 1961, pp. 123–160..Google Scholar
[12] Giladi, O., Naor, A., and Schechtman, G., Bourgain's discretization theorem. Ann. Fac. Sci. Toulouse Math. 21 (2012), no. 4, 817–837. http://dx.doi.org/10.5802/afst.1352 Google Scholar
[13] Gupta, A., Newman, I., Rabinovich, Y., and Sinclair, A., Cuts, trees and `1-embeddings of graphs. Combinatorica 24 (2004), no. 2, 233–269. http://dx.doi.org/10.1007/s00493-004-0015-x Google Scholar
[14] James, R. C., A separable somewhat reflexive Banach space with nonseparable dual. Bull. Amer. Math. Soc. 80 (1974), 738–743. http://dx.doi.org/10.1090/S0002-9904-1974-13580-9 Google Scholar
[15] James, R. C., Nonreflexive spaces of type 2 Israel J. Math. 30 (1978), no. 1–2. 1–13. http://dx.doi.org/10.1007/BF02760825 Google Scholar
[16] Johnson, W. B. and G. Schechtman, Diamond graphs and super-reflexivity. J. Topol. Anal. 1 (2009), no. 2, 177–189. http://dx.doi.org/10.1142/S1793525309000114 Google Scholar
[17] Kwapien, S., Isomorphic characterizations of inner product spaces by orthogonal series with vector valued coefficients. Studia Math. 44 (1972), 583–595. Google Scholar
[18] Lindenstrauss, J. and Rosenthal, H. P., The Lp spaces. Israel J. Math. 7 (1969), 325–349. http://dx.doi.org/10.1007/BF02788865 Google Scholar
[19] Lindenstrauss, J. and Stegall, C., Examples of separable spaces which do not contain `1 and whose duals are non-separable. Studia Math. 54 (1975), no. 1, 81–105. Google Scholar
[20] Lindenstrauss, J. and Tzafriri, L., Classical Banach spaces. Lecture Notes in Mathematics, 338, Springer-Verlag, Berlin-New York, 1973.Google Scholar
[21] Lindenstrauss, J. and Tzafriri, L., Classical Banach spaces. I. Sequence spaces. Ergebnisse der Mathematik und ihrer Grenzgebiete, 92, Springer-Verlag, Berlin-New York, 1977.Google Scholar
[22] Ostrovskii, M. I., On metric characterizations of some classes of Banach spaces. C. R. Acad. Bulgare Sci. 64 (2011), no. 6, 775–784. Google Scholar
[23] Ostrovskii, M. I., Metric embeddings. Bilipschitz and coarse embeddings into Banach spaces. De Gruyter Studies in Mathematics, 49, Walter de Gruyter, Berlin, 2013.Google Scholar
[24] Ostrovskii, M. I., On metric characterizations of the Radon–Nikod´ym and related properties of Banach spaces. J. Topol. Anal. 6 (2014), no. 3, 441–464. http://dx.doi.org/10.1142/S1793525314500186 Google Scholar
[25] Perrott, J. C. B., Transfinite duals of Banach spaces and ergodic super-properties equivalent to super-reflexivity. Quart. J. Math. Oxford Ser. (2) 30 (1979), no. 117, 99–111. http://dx.doi.org/10.1093/qmath/30.1.99 Google Scholar
[26] Pisier, G., Sur les espaces de Banach qui ne contiennent pas uniform´ement de `1 n. C. R. Acad. Sci. Paris S´er. A–B 277 (1973), A991–A994.Google Scholar
[27] Pisier, G., Martingales in Banach spaces. In preparation, 2014, preliminary version available at http://webusers.imj-prg.fr/_gilles.pisier/ihp-pisier.pdfGoogle Scholar
[28] Pisier, G. and Xu, Q., Random series in the real interpolation spaces between the spaces vp. In: Geometrical aspects of functional analysis. Lecture Notes Math., 1267, Springer, Berlin, 1987, pp. 185–209..Google Scholar
[29] Pták, V., Biorthogonal systems and reflexivity of Banach spaces. Czechoslovak Math. J. 9(84) (1959), 319–326. Google Scholar
[30] Stegall, C., The Radon–Nikod´ym property in conjugate Banach spaces. Trans. Amer. Math. Soc. 206 (1975), 213–223. http://dx.doi.org/10.1090/S0002-9947-1975-0374381-1 Google Scholar